作业车间调度问题(job shop scheduling problem, JSP)是许多现实工程生产的简化模型,因此研究JSP问题具有很强的工程生产背景,用智能算法对JSP的优化求解也成了企业提高生产效率的关键。目前的智能算法或多或少都存在着局限性。比如,遗传算法^[1-2]拥有较强的全局搜索能力但稳定性差、模拟退火算法^[3-4]拥有跳出局部最优解的能力但收敛速度慢,蚁群算法^[5-6]全局搜索能力强但存在汉明悬崖问题。部分学者倾向于将粒子群算法(particle swarm optimization, PSO)与其他算法混合以增强PSO全局搜索能力,但少有对PSO本身机理的研究,因此PSO在求解JSP问题上并无较大进展。例如,以求解JSP问题为例,文献[7]将遗传算子与PSO结合求解模糊作业车间调度问题,用粒子交叉变异公式取代了PSO的速度更新公式,但失去了PSO收敛速度快的优势;文献[8]将人工免疫算法与PSO结合求解装配车间作业调度问题,但是其参数根据经验选取,无法根据环境动态调整,限制了算法适应性;文献[9]将模拟退火与PSO结合求解周期作业车间调度问题,但是并未提出选取参数的方法,因而算法的全局搜索能力差。

本研究针对传统PSO种群初始解的质量差和全局搜索能力弱的缺点,使用改进粒子群算法(improved particle swarm optimization, IPSO)求解JSP问题。采用基于工序升序排列(ranked order value, ROV)的编码方式,得到粒子参数与工序序列的映射关系;在速度位置更新公式中采用自适应权重^[10],动态调整惯性系数和学习因子;在初始化种群中采用混沌映射^[11]和反向学习^[12]策略,提高种群初始解的质量;在算法迭代过程中引入莱维飞行^[13]和变邻域搜索^[14]策略,避免陷入局部最优解;在种群丧失多样性进化停滞时,采取混沌弹射机制激活个体,提高粒子利用率;通过试验验证IPSO的有效性。

JSP问题定义如下:存在n个工件,需要在m台机器上进行加工,每个工件需加工m道工序,每个工件的加工顺序和加工时间不同,已知每个工件的加工顺序和相应的加工时间,在满足工件约束和机器约束两个约束条件的情况下,寻求一种最理想的加工顺序方案,使得加工完成这个工件的加工时间最短。

对应的已知条件描述如下:

(1)工件加工工序集为O=[O₁  O₂  …  O_i  …  O_n]^T, O_i表示第i个工件包含的所有加工工序集, O_i=[O_i1  O_i2  …  O_ik  …  O_im], O_ik表示第i个工件的第k道加工工序, i=1, 2, …, n, k=1, 2, …, m;

(2)机器加工工序集为M=[M₁  M₂  …  M_j  …  M_m]^T, M_j表示第j台机器所需加工的工件集, M_j=[M_j1  M_j2  …  M_jh  …  M_jn], M_jh表示第j台机器上所加工的第h个工件, j=1, 2, …, m。h=1, 2, …, n;

(3)工件加工时间集OT=[OT₁  OT₂  …  OT_i  …  OT_n]^T, OT_i表示加工第i个工件所花费的总时间, OT_i=[OT_i1  OT_i2  …  OT_ik  …  OT_im], OT_ik表示第i个工件在第k台机器上加工完成的时间, i=1, 2, …, n, k=1, 2, …, m;

(4)机器加工时间集MT=[MT₁  MT₂  …  MT_j  …  MT_m]^T, MT_j表示第j台机器加工所花费的总时间, MT_j=[MT_j1  MT_j2  …  MT_jh  …  MT_jn], MT_jh表示第j台机器上第h个工件加工完成的时间, j=1, 2, …, m, h=1, 2, …, n。

在加工过程中满足的约束条件如下:

(1)每时刻每工机器只能加工一个工件,且过程不能被打断;

(2)各工件在规定的机器上的加工时间是已知的、固定的和一一对应的;

(3)各工件在每个加工机器上只加工一次;

(4)各工件有各自特定的工艺加工路线,且加工路线是事先确定的、不能更改的。

作业车间调度问题数学模型的目标函数如下:

(1) ${f^ * } = \min \left\{ {\max {\bf{M}}{{\bf{T}}_j}\left( {或\;\max {\bf{O}}{{\bf{T}}_i}} \right)} \right\},$

式中:f^*为求最短加工时间的目标函数。

作业车间调度问题数学模型的约束条件如下:

(2) $\left\{ \begin{array}{l}{\rm{M}}{{\rm{T}}_{jh}} \le {t_{{\rm{MP}}j\left( {h + 1} \right)}},h = 1,2, \cdots ,n - 1\\{\rm{O}}{{\rm{T}}_{ik}} \le {t_{{\rm{PM}}i\left( {k + 1} \right)}},k = 1,2, \cdots ,m - 1\\{\bf{M}}{{\bf{T}}_j} = {\rm{M}}{{\rm{T}}_{jn}}\\{\bf{O}}{{\bf{T}}_i} = {\rm{O}}{{\rm{T}}_{im}}\end{array} \right.,$

式中:t_MPjh为第j台机器上第h个工件加工的起始时间; t_PMik为第i个工件在第k台机器加工的起始时间。

由于粒子群算法中的“全局最优解”与普通意义的优化命题里的“全局最优解”有部分差异,为不引起歧义,本研究定义粒子群算法中的“全局最优解”为“当前全局最优解”,相对于目标搜索空间中真实存在的“理想全局最优解”,算法在当前时刻找寻到的已知的最优解为“当前全局最优解”,该解的质量低于或等于“理想全局最优解”。

传统的粒子群算法建立在一个抽象的D维目标搜索空间中,有n个粒子组成一个种群,第i个粒子在每次迭代进化过程中依据个体历史最优值P_i=[P_i1  P_i2  …  P_id  …  P_iD]和当前全局最优值G=[G₁  G₂  …  G_d  …  G_D]进行种群间的信息交流来实现自身的位置x_i=[x_i1  x_i2  …  x_id  …  x_iD]和速度v_i=[v_i1  v_i2  …  v_id  …  v_iD]的更新,从而整个种群不断地向当前全局最优解靠近^[15],其中, i=1, 2, …, n, d=1, 2, …, D。具体更新公式如下:

(3) $\left\{ \begin{array}{l}v_{id}^{s + 1} = \omega v_{id}^s + {c_1}{r_1}\left( {P_{id}^s - x_{id}^s} \right) + {c_2}{r_2}\left( {G_d^s - x_{id}^s} \right)\\x_{id}^{s + 1} = x_{id}^s + v_{id}^{s + 1}\end{array} \right.,$

式中:s表示当前迭代次数; v_id^s表示第s次迭代中第i个粒子在第d维度的速度分量; x_id^s表示第s次迭代中第i个粒子在第d维度的位置分量; ω表示惯性系数; c₁、c₂表示学习因子; r₁、r₂表示随机数; P_id^s表示截止到第s次迭代为止,第i个粒子在第d个维度位置分量的个体历史最优值; G_d^s表示截止到第s次迭代为止,第d个维度位置分量的全局历史最优值。

为克服传统粒子群早熟收敛的问题,改进粒子群算法将引入自适应策略、混沌序列、莱维飞行和变邻域搜索,以平衡全局和局部搜索能力。

由于编码内容要反映JSP问题的工件加工序列,所以本研究使用基于工序的编码方式,通过ROV规则^[16]建立粒子D维位置分量的连续参数与加工序列的离散值的映射关系,即每个粒子的位置分量便代表了一种加工顺序方案。以研究作业车间调度问题为例,对于n个工件m台机器的问题,建立有n×m道加工序列的二维向量编码和D维的粒子位置分量,其中D=n×m。

JSP问题以求解最短最大完工时间为最终目标,因此本研究设计改进粒子群算法的适应度函数

(4) ${\rm{Fit}}\left( i \right) = \frac{1}{{{T_{{\rm{pro}}}}\left( i \right)}},$

式中T_pro(i)为第i个粒子的加工方案所决定的加工时间。

(1)混沌初始化

在粒子群算法中,采用伪随机数生成的初始种群易产生较多的劣解使得个体集中在局部最优解,影响了算法的搜索能力^[17]。而混沌搜索^[11]的遍历性和随机性有利于初始群体摆脱局部最优值的束缚^[18]。本研究采用经典的混沌动力学模型logistic映射生成初始种群和初始种群解的表达式如下:

(5) ${z_{k + 1}} = 4 \times {z_k} \times \left( {1 - {z_k}} \right),k \in N,0 < {z_{k + 1}} < 1,$

(6) ${z_0} = {\rm{rand}},{\rm{rand}} \in \left( {0,1} \right),{\rm{rand}} \ne 0,0.25,0.5,0.75,1,$

式中:z_k表示混沌序列; rand表示随机数。

(7) ${\mathit{\boldsymbol{x}}_i} = \left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{z}}_{\left( {i - 1} \right) \times D + 1}}}&{{\mathit{\boldsymbol{z}}_{\left( {i - 1} \right) \times D + 2}}}& \cdots &{{\mathit{\boldsymbol{z}}_{\left( {i - 1} \right) \times D + D}}}\end{array}} \right],i = 1,2, \cdots ,n。$

由于混沌系统对初值具有极敏感性,所以首先产生一个随机数rand作为混沌序列的初始种子。根据式(5)产生n×D个混沌映射值,根据式(7)得到第i个粒子位置维度,并编码得到相应的加工序列。

(2)反向学习策略

反向学习^[12]策略即利用原解产生原解的反向解,在比较两个解的优劣后最终保留优势解。在本研究中,利用混沌映射产生初始群体后,产生反向解公式如下:

(8) $\mathit{\boldsymbol{x}}_{id}^ * = a + b - {x_{id}},$

式中:x_id^*表示第i个粒子第d维的位置维度的反向解; x_id为第i个粒子第d维的位置维度值; a, b分别为x_id取值范围的上下限。

(9) $\mathit{\boldsymbol{x}}_i^ * = \left[ {\begin{array}{*{20}{c}}{x_{i1}^ * }&{x_{i2}^ * }& \cdots &{x_{iD}^ * }\end{array}} \right],$

式中:x_i^*表达第i个反向粒子。

根据式(9)产生n个反向粒子组成种群大小与原种群相等的反向种群,再由式(4)计算的适应度值,最后将两个种群合并后排序,选取适应度值高的前50%作为最终起始粒子群。

(1)自适应策略

本研究基于自适应策略^[10],考虑到既需要增强粒子的全局搜索能力又要兼顾局部搜索能力,根据各个粒子的适应度不同,设置了动态调整各粒子的自适应权重如下:

(10) $\alpha = \left\{ \begin{array}{l}{\alpha _{\max }} - \left( {{\alpha _{\max }} - {\alpha _{\min }}} \right) \times \frac{{{T_{{\rm{pro}}}}\left( i \right) - {T_{\min }}}}{{{T_{avg}} - {T_{\min }}}},{\rm{Fit}}\left( i \right) \le {\rm{Fi}}{{\rm{t}}_{{\rm{avg}}}}\\{\alpha _{\max }},{\rm{Fit}}\left( i \right) > {\rm{Fi}}{{\rm{t}}_{{\rm{avg}}}}\end{array} \right.,$

式中:α可表示惯性系数ω或学习因子c, T_avg表示所有粒子的平均加工时间, T_min表示所有粒子的最小加工时间; Fit_avg表示所有粒子的平均适应度。

当粒子适应度值较群体平均适应度值低时,粒子有较强的全局搜索能力,即较大的α;当粒子跨过平均值门槛时,粒子拥有较强的局部搜索能力,即较小的α;而当粒子接近当前全局最优解时,粒子拥有较强的全局搜索能力以跳出局部最优解,即较大的α。

(2)莱维飞行

莱维飞行具有局部搜索和全局搜寻相结合的特征,能够增大搜索范围、丰富种群多样性和跳出局部最优解^[19]。因此,本研究采用文献[20]的蒙塔纳算法模拟莱维分布生成随机行走代替速度位置公式中的随机数rand。蒙塔纳算法如下:

(11) ${\rm{Levy}}\left( \beta \right) = \frac{X}{{{{\left| Y \right|}^{\frac{1}{\beta }}}}},X \sim N\left( {0,{\sigma ^2}} \right),Y \sim N\left( {0,1} \right),$

(12) ${\sigma ^2} = {\left\{ {\frac{{\Gamma \left( {1 + \beta } \right) \times \sin \left( {\frac{{{\rm{ \mathsf{ π} }} \times \beta }}{2}} \right)}}{{\beta \times \Gamma \left( {\frac{{{\rm{1}} + \beta }}{2}} \right) \times {2^{\frac{{\beta - 1}}{2}}}}}} \right\}^{\frac{1}{\beta }}},$

式中:β为^{[1, 2]}之间的参数, Γ为标准伽马函数。

(3)改进的速度位置更新公式

因此,综上所述,本研究改进的速度位置更新公式如下:

(13) $\left\{ \begin{array}{l}v_{id}^{s + 1} = \omega _i^sv_{id}^s + c_{1i}^s{\rm{Levy}}\left( \beta \right)\left( {P_{id}^s - x_{id}^s} \right) + c_{2i}^s{\rm{Levy}}\left( \beta \right)\left( {G_d^s - x_{id}^s} \right)\\x_{id}^{s + 1} = x_{id}^s + v_{id}^{s + 1}\end{array} \right.,$

式中:ω_i^s、c_1i^s和c_2i^s分别为第s次迭代中第i个粒子的自适应惯性系数、自适应个体学习因子和自适应全局学习因子。

(1)混沌弹射机制

当粒子到达当前全局最优点时,对该粒子采取混沌初始化的方式,重置该粒子的位置维度值,使粒子在空间其他不确定的位置出现,类似于将粒子从最优点的位置“弹射”出去。

(14) ${\rm{if}}\;{\rm{Fit}}\left( i \right) = {\rm{Fi}}{{\rm{t}}_{{\rm{best}}}},$

(15) ${\rm{then}}\;{\mathit{\boldsymbol{x}}_i} = {\rm{Chaos}}\left( {{x_i}} \right),$

式中:Fit_best表示所有粒子的当前全局最优值; Chaos函数表示根据第2.3.1节的混沌原理将第i个粒子的D维位置维度重新初始化。

由于混沌映射的遍历性和非重复性,扩展粒子的搜索空间,提高算法中粒子的利用率,比目前的变异机制更有效果。

(2)变邻域搜索

变邻域搜索^[21](variable neighborhood search, VNS)是一种重要的元启发式搜索算法,通过搜索给定邻域结构集合中系统的变化邻域结构来扩展搜索范围。潘全科指出,两种邻域结构局部最优解之间的距离往往较近^[22]。基于上述观点,本研究采用3种邻域结构的搜寻算子^[23],对当前全局最优粒子执行变邻域操作后进行适应度值计算并比较,保留适应度值高的粒子。

①交换。在D道加工序列中随机交换两不同工序的位置,结果如下:

(16) $\mathit{\boldsymbol{o}} = \left[ {\begin{array}{*{20}{c}} {{o_1}}& \cdots &{{o_r}}& \cdots &{{o_q}}& \cdots &{{o_D}} \end{array}} \right]\xrightarrow{{{\text{exchange}}}}{\mathit{\boldsymbol{o}}^ * } = \left[ {\begin{array}{*{20}{c}} {{o_1}}& \cdots &{{o_q}}& \cdots &{{o_r}}& \cdots &{{o_D}} \end{array}} \right];$

②插入。在D道加工序列中随机选择某一加工序列插入到另一位置较小的前面,结果如下:

(17) $\mathit{\boldsymbol{o}} = \left[ {\begin{array}{*{20}{c}} {{o_1}}& \cdots &{{o_r}}& \cdots &{{o_q}}& \cdots &{{o_D}} \end{array}} \right]\xrightarrow{{{\text{insert}}}}{\mathit{\boldsymbol{o}}^ * } = \left[ {\begin{array}{*{20}{c}} {{o_1}}& \cdots &{{o_q}}&{{o_r}}& \cdots &{{o_D}} \end{array}} \right];$

③倒序。在D道加工序列中随机选择一段加工序列进行倒序操作,结果如下:

(18) $\mathit{\boldsymbol{o}} = \left[ {\begin{array}{*{20}{c}} {{o_1}}& \cdots &{{o_r}}&{{o_{r + 1}}}& \cdots &{{o_{r + q}}}& \cdots &{{o_D}} \end{array}} \right]\xrightarrow{{{\text{back}}}}{\mathit{\boldsymbol{o}}^ * } = \left[ {\begin{array}{*{20}{c}} {{o_1}}& \cdots &{{o_{r + q}}}&{{o_{r + q - 1}}}& \cdots &{{o_r}}& \cdots &{{o_D}} \end{array}} \right],$

式中:o为原加工序列, o^*为执行变邻域操作后的新加工序列。

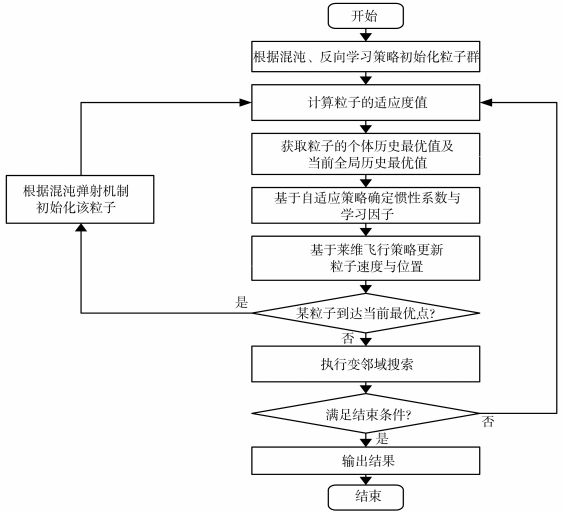
基于上述的改进粒子群算法,下面叙述算法解决JSP问题的步骤及流程图(如图1所示)。

步骤1  根据混沌及反向学习策略,初始化粒子群的位置与速度;

步骤2  计算各粒子的适应度值,并记录个体与当前全局的历史最优,同时计算粒子适应度平均值;

步骤3  基于自适应学习策略,确定各个粒子的自适应惯性系数与学习因子;

步骤4  基于莱维飞行策略更新各个粒子的位置与速度,并更新个体与当前全局的历史最优;

步骤5  判断有无粒子到达当前全局最优点,若有则根据混沌弹射机制重置粒子,该粒子返回步骤2;

步骤6  对当前全局最优点执行变邻域搜索,更新当前全局最优解;

步骤7  若满足结束条件,则输出最终结果,否则返回步骤2。

为了判断算法的优缺点,需要用相同标准的问题去测试。标准问题给出了评判所有用于求解JSP问题的算法的共同标准,由于不同的标准问题有着不同的维度数与难易度,因此可以使用这些标准问题验证算法的性能^[24]。本研究采用标准问题测试库中的Fisher与Thompson在1963年提出的FT系列^[25]和Lawrence于1984年给出的LA系列^[25]的部分问题,其均用于求解JSP和验证算法性能。为验证本研究改进粒子群算法的有效性,以下结果将与传统粒子群算法进行试验对比。

算法采用MATLAB编程,在2.40 GHz处理器的Windows10系统下运行。本研究的改进粒子群算法设置迭代次数200次,粒子数量为200, ω_max和ω_min分别为0.8和0.6, c_max和c_in的取值分别为1.2和0.8,变邻域搜索迭代次数50次;传统粒子群算法设置迭代次数200,粒子数量为200, ω、c设为1。每种算法每个算例连续独立运行20次。

由表1可以看出,虽然IPSO算法仅找到了FT06的已知最优值,但是IPSO算法相较于PSO算法,大大提高了找到LA01、LA06、LA11算例的已知最优值的寻优成功率,并且在平均值可以看出改进算法相较传统算法稳定性更强,有更强的鲁棒性。在最小值提升率和平均值提升率中也可以看出改进的算法比传统的粒子群算法更有优势。

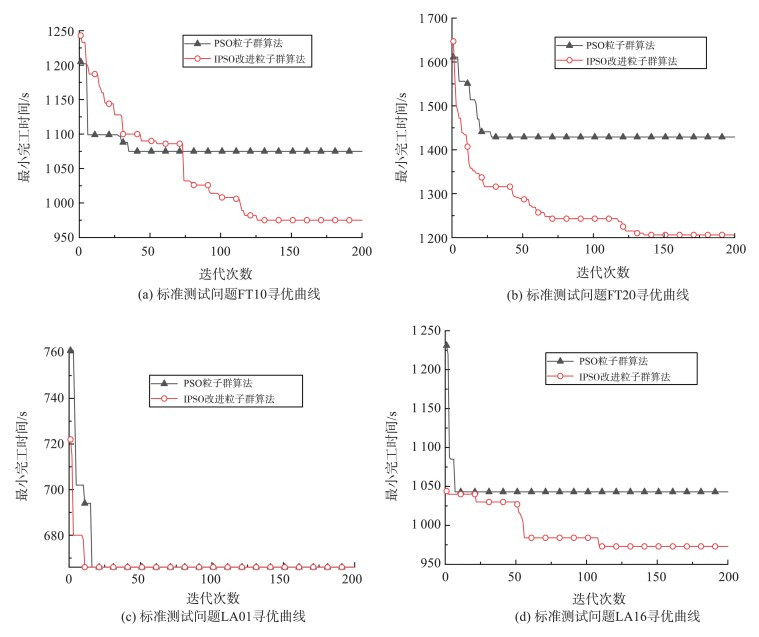
由图2可以看出,在求解FT10问题和FT20问题时,虽然两种算法有相同解,但IPSO算法拥有更强的跳出局部最优解的能力;在求解LA01问题时,虽然两种算法都找到了目前已知最优解,但IPSO算法效率更高、速度更快;在求解LA16问题时, IPSO算法拥有质量更优的种群初始解和更强的跳出局部最优解的能力。所以,相较于传统的PSO算法, IPSO算法提高了传统算法的全局搜索能力,且增强了粒子群摆脱局部最优解的能力,丰富了种群在迭代后期的多样性,找到了更优的解,相较传统算法来说拥有更强的鲁棒性和实用性。

本研究针对JSP问题,对传统粒子群算法的不足进行改进。首先提出基于自适应策略的惯性系数和加速因子,使得粒子群算法的系数得以随适应度值进行动态调整,平衡了算法在不同环境中的全局搜索和局部搜索能力;还引入混沌映射及反向学习机制优化了群体初始的适应度值,提升了算法的求解效率;又引入莱维飞行、变邻域搜索和混沌弹射机制增强了算法跳出局部最优解的能力,有效地缓解了早熟收敛的问题。

仿真试验结果表明,改进粒子群算法的粒子利用率高、效率高,搜寻能力强,能在不同规模的问题中找到更好的解,算法的鲁棒性更强,在求解JSP问题上拥有更大的优势,为粒子群算法的改进方向提供了研究思路,并且对实际工程生产也有一定的指导作用。对于FT10以上规模的问题,本研究算法暂时未能找到更优解,因此提高改进粒子群算法对于大规模JSP问题的适应性将是未来研究的重要方向。