2. 大连海事大学轮机工程学院, 辽宁 大连 116026
2. Marine Engineering College, Dalian Maritime University, Dalian 116026, Liaoning, China
随着海洋科技和控制技术的飞速发展, 水面无人艇(unmanned surface vessels, USV)控制技术也得到了飞速的发展[1]。USV具有机动性强、便于隐蔽、可搭载在其他舰艇上等优点, 在搜救、海洋环境探测、海洋调查以及海事维权中得到了广泛的应用[2]。为了便于实现大规模的自主作业, USV路径跟踪及编队控制成为当前重要的研究方向[3]。
目前在USV路径跟踪控制的研究中[4-9], 主要存在以下的难点:(1)随USV航行速度的变化, 水动力系数将随之改变, 而且风、浪、流等海洋环境也产生各种未知的干扰, 因此系统具有高度不确定性、时变性和非线性特点; (2)与其他水面船舶一样, USV没有横向的驱动能力, 因此具有明显的欠驱动特性, 目前很多的非线性控制算法不能直接应用到欠驱动系统中。文献[6]基于PID控制算法设计了路径跟踪策略, 实现方法较为简单, 但从试验结果中可以看出, 在风、浪、流等外界干扰下, 取得的控制效果很有限。文献[7-8]基于神经网络算法设计了路径跟踪控制器, 可以不依赖于被控对象的数学模型, 但需要对神经网络进行在线或离线学习, 并利用训练结果进行控制。文献[9-10]基于滑模变结构控制方法设计了一种轨迹跟踪控制律, 并在水池中进行了试验验证, 但在设计中没有考虑环境干扰力对控制系统的影响, 而且存在轨迹起点必须在期望轨迹上的限制和不能等速跟踪圆轨迹等缺陷。
自抗扰控制算法(active disturbance rejection control, ADRC)是在PID控制算法的基础上发展起来的, 基本原理是把作用于被控对象的所有不确定性因素都归结为未知扰动, 然后利用被控对象的输入和输出数据对它进行估计和补偿[11]。由于既不要求被控对象有精确的数学模型, 也不需要事先知道扰动作用的规律, 因而ADRC算法简单、鲁棒性强、便于实现, 在提出后得到了广泛的使用。近年来, ADRC已经成功地应用到了汽油发动机控制[12]、船舶航向航迹[13-14]、无人水下航行器[15]等控制领域。但由于自抗扰控制器参数众多, 没有成熟的理论作为参数调整的依据, 文献[13-14]依靠经验调整参数, 难以达到最优控制效果。文献[15-16]将基于单种群的遗传算法应用到了自抗扰控制器的参数整定中, 利用遗传算法的全局优化特性寻找最佳的个体适应度, 但遗传算法本身容易陷于局部最优的问题没有得到解决。文献[17]提出了一种利用混沌运动的遍历性的多目标遗传算法。文献[18-19]提出了一种双种群遗传算法, 用于解决单种群遗传算法容易陷于局部最优的问题。
本研究针对实现无人艇编队控制中首先需要实现的单个无人艇路径跟踪问题进行研究, 设计了USV到达指定路径的方法和路径跟踪自抗扰控制器, 然后引入基于混沌局部搜索策略的双种群遗传算法(dual population genetic algorithm with chaotic local search, CLSDPGA)来解决ADRC参数的优化问题。试验结果表明经CLSDPGA优化的自抗扰控制器可有效解决欠驱动水面无人艇的路径跟踪控制问题, 对海洋环境的不确定动态、未知扰动以及模型的参数摄动具备良好的稳定性和鲁棒性。
1 水面无人艇数学模型分析航行中的水面无人艇运动具有6个自由度, 分别由沿着X、Y、Z轴方向的线性速度和沿着X、Y、Z轴旋转方向的角速度构成。这6个自由度的运动可用表 1所示的国际船模试验水池会议推荐的SNAME (society of naval architects and marine engineers)表示法来描述。
| 表 1 SNAME表示法 Table 1 SNAME representation |
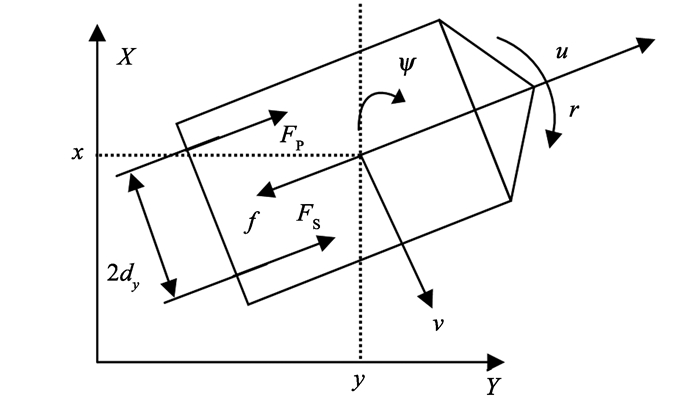
水面无人艇运动的示意图见图 1。在本研究中, 仅考虑USV在海平面上的3个自由度方向的运动, 即前进方向(x, u)、横漂方向(y, v)以及偏航方向(ψ, r)。
|
图 1 水面无人艇平面运动模型 Figure 1 USV planar motion model |
USV的运动可由三自由度的运动方程来描述[20], 其中运动学方程为
| $ \boldsymbol{\dot \eta} = R\left( \boldsymbol{\eta} \right)\boldsymbol{V} = \left[ {\begin{array}{*{20}{c}} {\cos \left( \psi \right)}&{ - \sin \left( \psi \right)}&0\\ {\sin \left( \psi \right)}&{\cos \left( \psi \right)}&0\\ 0&0&1 \end{array}} \right]\left[ \begin{array}{l} u\\ v\\ r \end{array} \right], $ | (1) |
式中η=[xyψ]T, V=[uvr]T。
动力学方程为
| $ \boldsymbol{M\dot V} + \boldsymbol{C}\left( \boldsymbol{V} \right)\boldsymbol{V} + \boldsymbol{DV} + \Delta f\left( \boldsymbol{V} \right) = \boldsymbol{\tau} , $ | (2) |
式中:
| $ \begin{array}{l} \boldsymbol{M} = {\boldsymbol{M}^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} {{m_{11}}}&0&0\\ 0&{{m_{22}}}&{{m_{23}}}\\ 0&{{m_{32}}}&{{m_{33}}} \end{array}} \right];\\ \boldsymbol{C}\left( \boldsymbol{V} \right) = \left[ {\begin{array}{*{20}{c}} 0&0&{ - {m_{23}}v - {m_{23}}r}\\ 0&0&{{m_{11}}u}\\ {{m_{22}}v + {m_{23}}r}&{ - {m_{23}}u}&0 \end{array}} \right];\\ \boldsymbol{D} = \left[ {\begin{array}{*{20}{c}} {{d_{11}}}&0&0\\ 0&{{d_{22}}}&{{d_{23}}}\\ 0&{{d_{32}}}&{{d_{33}}} \end{array}} \right];\\ \boldsymbol{\tau} = {\left[ {\begin{array}{*{20}{c}} {{\tau _u}}&{{\tau _v}}&{{\tau _r}} \end{array}} \right]^{\rm{T}}} \end{array} $ |
其中, M∈R3×3表示惯性坐标系下的惯性矩阵, C(V)∈R3×3表示科里奥利与向心力矩阵, D∈R3×3表示水动力阻尼矩阵, Δf(V)∈R3表示系统中未建模的动态力及参数扰动; τ∈R3表示螺旋桨推力和转向力矩。
对于图 1所示的欠驱动水面无人艇, 由于缺少横向的驱动力, 因此一般情况下取τv=0。前进方向上的螺旋桨推力τu=FP+FS, 转向控制力矩τr=(FP-FS)·dy。
2 路径跟踪方法USV路径跟踪中, USV首先要从初始位置到达指定路径, 然后沿指定路径航行。为了使无人艇从海平面上任意位置快速运动到指定的路径上, 在控制中常用的方法是最近会遇点法[3]。该方法是一种几何方法, 通过无人艇当前位置向目标航线做垂线, 从而确定目标路径上与初始位置距离最近的点pd=[xd, yd]T。然而在复杂的规划路径中, 往往很难通过几何法直接找出, 可以利用控制理论中的优化算法来找出目标点[21-23]。
首先将规划路径参数化, 即路径上的每个点都可以用参数λ表达: p(λ)=[x(λ), y(λ)]T, 无人艇的当前位置为p(t)=[x(t), y(t)]T, 则无人艇距离目标点的距离可以e=p(t)-pd(λ)表示, 通过性能函数J(λ)=0.5eTe可以计算出最近的会遇点。需要注意的是, 随着水面无人艇位置的变化, 需要动态调整目标点的位置。然后, 可以根据目标点坐标, 确定水面无人艇的参考航向
| $ {\psi _{{\rm{ref}}}} = {\rm{a}}\tan 2\left( {\frac{{{y_d}\left( {\lambda + \Delta } \right) - y\left( t \right)}}{{{x_d}\left( {\lambda + \Delta } \right) - x\left( t \right)}}} \right), $ | (3) |
式中:Δ是为了引导水面无人艇跟踪指定路径而叠加的一个引导参数, Δ的值可以根据水面无人艇的航行速度u以及路径特性确定。
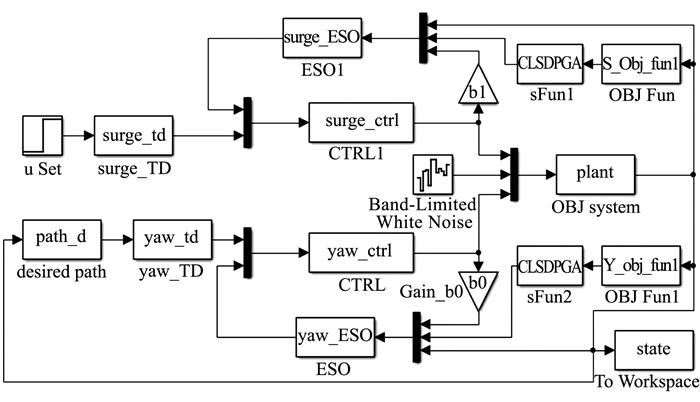
3 路径跟踪自抗扰控制器设计 3.1 自抗扰控制器设计从PID发展而来的自抗扰控制器与非线性PID的区别[11]主要在于:(1)通过跟踪微分器(tracking differentiator, TD)给输入信号安排了过渡过程, 并提供了输入信号的微分, 而且二阶的跟踪微分器还可以起到对输入信号的滤波作用; (2)扩张状态观测器(extended state observer, ESO)不仅能够实现对系统状态的观测, 还能实现对扰动的估计, 从而实现对扰动的补偿。自抗扰控制器本身不要求被控对象精确数学模型的本质, 就在于它会将被控对象数学模型中未建模的部分、参数的摄动以及所受的所有扰动全都通过扩张状态观测器予以补偿和消除。本研究设计的水面无人艇路径跟踪自抗扰控制器如图 2所示。
|
图 2 路径跟踪自抗扰控制器结构 Figure 2 Structure of path following ADRC |
该控制系统由航速和航向两个子控制系统组成。航速自抗扰控制器完成对航速的控制, 而航向自抗扰控制器则通过路径跟踪控制算法给出的修正航向完成路径跟踪控制。自抗扰控制算法的离散化算式为:
| $ \left\{ \begin{array}{l} {\rm{fv = fhan}}\left( {{v_1} - v,{v_2},{r_0},h} \right),\\ {v_1} = {v_1} + h \cdot {v_2},\\ {v_2} = {v_2} + h \cdot {\rm{fv}}\\ e = {z_1} - y,\\ {z_1} = {z_1} + h \cdot {z_2} - {\beta _{01}}e,\\ {z_2} = {z_2} + h \cdot \left( {{z_3} + {b_0}u} \right) - {\beta _{02}}{\rm{fal}}\left( {e,0.5,h} \right),\\ {z_3} = {z_3} - {\beta _{03}}{\rm{fal}}\left( {{e_1},0.25,h} \right),\\ {e_1} = {v_1} - {z_1},{e_2} = {v_2} - {z_2},\\ {u_0} = {\alpha _1}{\rm{fal}}\left( {{e_1},0.75,h} \right) + {\alpha _2}{\rm{fal}}\left( {{e_2},1.5,h} \right),\\ u = - \frac{{{u_0} + {z_3}}}{{{b_0}}} \circ \end{array} \right. $ | (4) |
式中:r0为快速因子, 与被控对象的控制能力有关, 在航速控制系统中, r0越大, 无人艇的螺旋桨的最大推力也就要求越大; h为采样时间; 非线性函数fhan(·)以及fal(·)的表示形式和自抗扰控制的收敛性分析过程可参考文献[11, 24], 在此不再赘述。
3.2 基于CLSDPGA的控制器参数整定每个ADRC中有8个参数需要调整, 通过“试凑法”可以得到参数的大致范围, 然后再利用CLSDPGA算法对控制器的参数进行优化整定。该算法采用双种群遗传算法实现全局范围内更好地寻优, 同时利用混沌系统的遍历性来进行局部范围内无重复搜索, 提升局部搜索的效率。本研究中仅简要描述参数优化过程, 具体过程见文献[25]。
(1)参数编码
将速度自抗扰控制器和航向自抗扰控制器的控制参数组成一个向量参数ζ, 然后对ζ进行实数编码组成个体。
| $ \boldsymbol{\zeta} = \left[ {\begin{array}{*{20}{c}} {{\beta _{u01}}}&{{\beta _{u02}}}&{{\beta _{u03}}}&{{\alpha _{u1}}}&{{\alpha _{u2}}}&{{\alpha _{u0}}}\\ {{\beta _{r01}}}&{{\beta _{r02}}}&{{\beta _{r03}}}&{{\alpha _{r1}}}&{{\alpha _{r2}}}&{{\alpha _{r1}}} \end{array}} \right] \circ $ |
(2)种群初始化
设定种群规模为30, 探测种群的交叉概率为Pc1, 变异概率为Pm1, 开发种群的交叉概率和变异概率分别为Pc2和Pm2, 种群的最大进化代数为Gmax, 输入变量的上界和下界分别为H和L, 则初始种群为:P=L+rand(1)(H-L)。
(3)参数优化
为获得较好的系统动态特性, 同时兼顾系统能量和操舵频度, 选取式(5)所示的适应度函数, 对探测种群和开发种群执行Logistic映射的混沌局部搜索算法, 选取最佳个体。
| $ J = \int_0^\infty {\left( {{w_1}|e\left( t \right)| + {w_2}\tau _r^2\left( t \right) + {w_3}{k^2}} \right)} dt, $ | (5) |
(4)条件判断
如果进化代数满足移民条件, 则执行种群移民操作; 如果进化代数等于Gmax, 则终止优化过程, 并输出最优控制器参数。
4 仿真结果分析为验证算法的有效性, 下面进行仿真试验, 仿真模型中的各参数[3]如下: m11=m22=33kg, m33=10kg·m2, m23=m32=3.3kg·m, d11=d22=d33=5, d23=d32=0。
考虑到USV螺旋桨的推进能力和转向能力, 系统的最大推进力Fmax=100N和最大转向力矩Tmax=50N·m。
给定无人艇的初始状态为:
| $ \begin{array}{l} \boldsymbol{\eta} = {\left[ {\begin{array}{*{20}{c}} {5{\rm{m}}}&{0{\rm{m}}}&{ - 2.8274{\rm{rad}}} \end{array}} \right]^{\rm{T}}},\\ \boldsymbol{V} = {\left[ {\begin{array}{*{20}{c}} { - 0.1{\rm{m/s}}}&{0.5{\rm{m/s}}}&{0rad/s} \end{array}} \right]^{\rm{T}}} \circ \end{array} $ |
经过CLSDPGA算法优化后, 最终得到速度自抗扰控制器的参数为:
TD: r0=0.1, h=0.01;
ESO: βu01=1, βu02=3, βu03=10, bu0=0.01;
NLSEF: αu1=100, αu2=4.5。
航向自抗扰控制器优化后的参数为:
TD: r0=2, h=0.01;
ESO: βr01=1, βr02=2, βr03=10, br0=0.02;
NLSEF: αr1=10, αr2=13。
4.2 直线路径跟踪结果分析通过直线路径观察自抗扰控制器的路径跟踪能力, 给定路径的数学描述式为:
| $ \left\{ \begin{array}{l} {x_d} = 8,\\ {y_d} = 2 + \frac{{t \times 30}}{{120}} \circ \end{array} \right. $ | (6) |
无人艇的初始航速设定为0.2m/s, 在第30s时航速设定为0.3m/s。直线路径的跟踪结果如图 3和图 4所示。

|
图 3 直线路径跟踪 Figure 3 Straight-line path following |
|
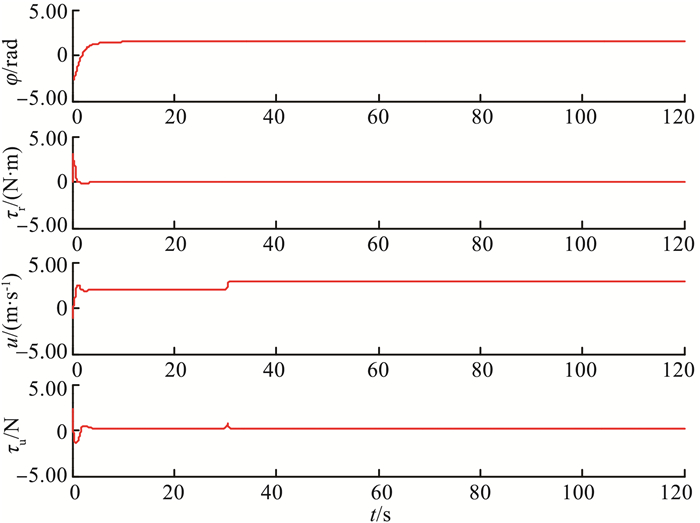
图 4 直线路径跟踪中的控制量和输出量 Figure 4 Input and output in straight-line path following |
图 3展示了直线路径跟踪过程中的实际轨迹和期望轨迹的对比。可以看出, 该控制器能快速地到达给定路径, 并很好地跟踪设定路径。图 4展示了路径跟踪过程中USV的航向、转向力矩、航速以及推进力。可以看出跟踪过程中推进力和转向力矩输出平滑, 对航速的变化具备良好的控制性能。
4.3 曲线路径跟踪结果分析 4.3.1 圆形路径通过圆形路径观察自抗扰控制器跟踪曲线路径的能力, 给定路径的数学描述式为:
| $ \left\{ \begin{array}{l} {x_{\rm{d}}} = 4\cos \left( { - \frac{{2{\rm{\pi }}}}{{100}}{\rm{t}}} \right),\\ {y_{\rm{d}}} = 4\sin \left( { - \frac{{2{\rm{\pi }}}}{{100}}{\rm{t}}} \right) \circ \end{array} \right. $ | (7) |
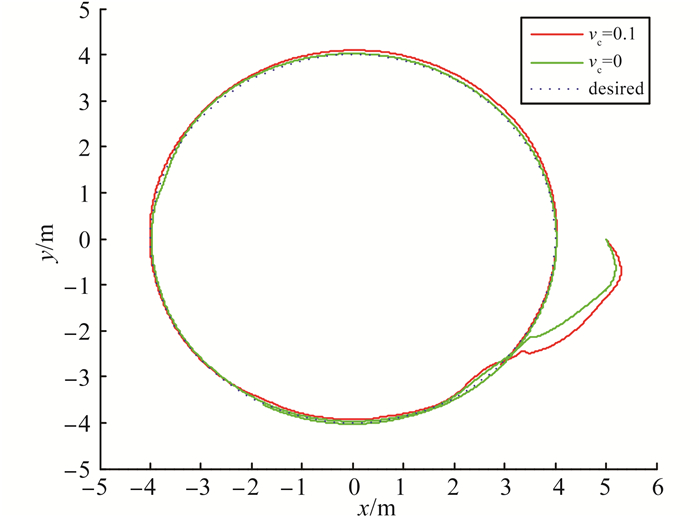
初始航速为0.2m/s, 在第60s时航速变为0.3m/s。同时为了模拟环境干扰和海流干扰, 对无人艇施加幅值为0.5的白噪声干扰和恒定的海流干扰vc=0.1m/s。仿真结果如图 5、6所示。
|
图 5 带干扰的圆形路径跟踪 Figure 5 Circle path following with disturbance |
|
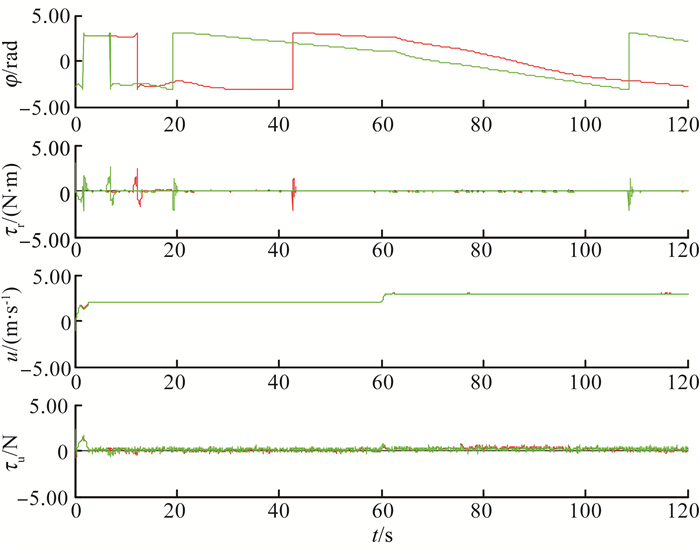
图 6 圆形路径跟踪中的输入和输出 Figure 6 Input and output in circle path following |
从图 5可以看出, 施加的环境干扰和恒定的海流干扰对系统的路径跟踪结果带来的影响不大, 能很好地跟踪期望路径。圆形路径的仿真结果表明最终的USV航向和航速比较稳定, 这不仅说明该控制器能实现较好的圆形路径跟踪, 也说明自抗扰控制器对外部未知干扰具备很好的抑制能力。分析图 6可知, 海流干扰会影响USV的参考航向, 而随机的白噪声干扰对跟踪过程中的推进力和转向力矩影响较大, 说明海况较差时操舵将变得十分频繁。
4.3.2 正弦路径为了进一步观察该控制器的路径跟踪能力, 再给定一种正弦形状的路径, 前进方向上周期为20m, 振幅为4m, 数学描述式为:
| $ \left\{ \begin{array}{l} {x_{\rm{d}}} = 3 - 4\sin \left( {{y_{\rm{d}}} - 2} \right),\\ {y_{\rm{d}}} = 2 + \frac{{2{\rm{\pi t}}}}{{120}} \circ \end{array} \right. $ | (8) |

|
图 7 正弦路径跟踪 Figure 7 Sinusoidal path following |
|
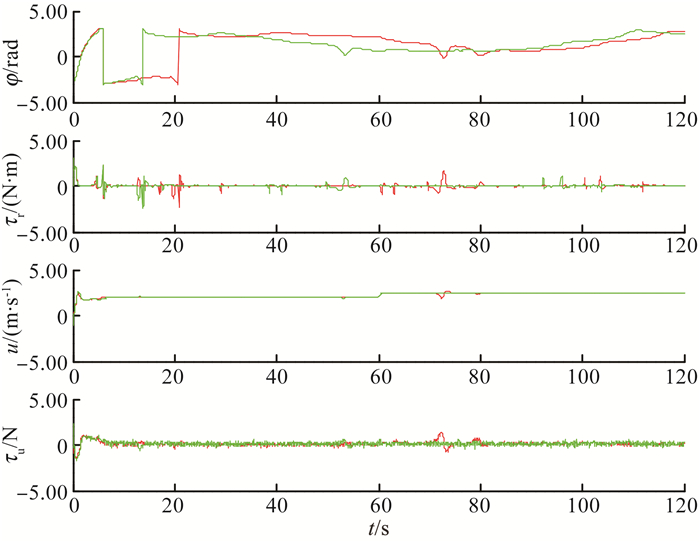
图 8 正弦路径跟踪中的输入和输出 Figure 8 Input and output in sinusoidal path following |
在正弦波的顶点处, 随着航速的不断降低以及转向率的不断增加, USV的欠驱动特性将表现得十分明显, 从而造成较大的跟踪误差。图 7和图 8表明, 基于自抗扰控制的路径跟踪控制器能较好地跟踪正弦路径, 说明该控制器对该欠驱动系统具备较好的控制能力, 对随机未知的外部干扰和恒值干扰都具备很好的鲁棒性。
5 结语本研究基于自抗扰控制算法设计了水面无人艇路径跟踪控制器, 通过CLSDPGA算法对自抗扰控制器的参数进行了优化调整。仿真试验结果分析表明,本研究设计的欠驱动水面无人艇路径跟踪自抗扰控制器对海洋环境的不确定动态、未知扰动以及模型的参数摄动具备良好的稳定性和鲁棒性。本研究为解决欠驱动水面无人艇非线性系统控制问题和自抗扰控制器的参数整定提供了一种新的思路和方法。下一步拟将该方法应用于水面无人艇的编队控制。
| [1] |
李家良. 水面无人艇发展与应用[J].
火力与指挥控制 , 2012, 37 (6) : 203-207 LI Jialiang. Development and application of unmanned surface vehicle[J]. Fire Control & Command Control , 2012, 37 (6) : 203-207 (  0) 0)
|
| [2] |
胡云艳.欠驱动水面无人艇的航迹跟踪控制研究[D].哈尔滨:哈尔滨工程大学, 2011.
HU Yunyan. Research on tracking control of underactuated unmanned surface vessels[D]. Harbin: Harbin Engineering University, 2011. http://cdmd.cnki.com.cn/article/cdmd-10217-1012264478.htm (  0) 0)
|
| [3] |
LIU L, WANG D, PENG Z H. Direct and composite iterative neural control for cooperative dynamic positioning of marine surface vessels[J].
Nonlinear Dynamics , 2015, 81 (3) : 1315-1328 DOI:10.1007/s11071-015-2071-8 ( 0) 0)
|
| [4] |
YAN Z P, YU H M, ZHANG W, et al. Globally finite-time stable tracking control of underactuated UUVs[J].
Ocean Engineering , 2015, 107 : 132-146 DOI:10.1016/j.oceaneng.2015.07.039 ( 0) 0)
|
| [5] |
王飞飞, 闫雪华, 刘允刚. 一类控制系数未知非线性参数化系统的输出反馈实际跟踪控制[J].
山东大学学报(工学版) , 2013, 43 (5) : 55-67 WANG Feifei, YAN Xuehua, LIU Yungang. Practical tracking by output feedback for a class of nonlinearly parameterized systems with unknown control coefficients[J]. Journal of Shandong University (Engineering Science) , 2013, 43 (5) : 55-67 (  0) 0)
|
| [6] |
DALY J, TRIBOU M, WASLANDER S. A nonlinear path following controller for an underactuated unmanned surface vessel[C]// Proceedings of 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. Algarve, Portugal: Intelligent Robots and Systems, 2012: 82-87.
( 0) 0)
|
| [7] |
DONG Z P, WAN L, LI Y M, et al. Trajectory tracking control of underactuated USV based on modified backstepping approach[J].
International Journal of Naval Architecture and Ocean Engineering , 2015, 7 (5) : 817-832 ( 0) 0)
|
| [8] |
高双, 朱齐丹, 李磊. 基于神经网络的高速无人艇模糊PID控制[J].
系统仿真学报 , 2007, 19 (4) : 776-779 GAO Shuang, ZHU Qidan, LI Lei. Fuzzy NN control of high-speed unmanned ship[J]. Journal of System Simulation , 2007, 19 (4) : 776-779 (  0) 0)
|
| [9] |
LIU C, ZOU Z J, LI T S. Path following of underactuated surface vessels with fin roll reduction based on neural network and hierarchical sliding mode technique[J].
Neural Computing & Applications , 2015, 26 (7) : 1525-1535 ( 0) 0)
|
| [10] |
ASHRAFIUON H, MUSKE K, MCNINCH L, et al. Sliding-mode tracking control of surface vessels[J].
IEEE Transactions on Industrial Electronics , 2008, 55 (11) : 4004-4011 DOI:10.1109/TIE.2008.2005933 ( 0) 0)
|
| [11] |
HAN J Q. From PID to active disturbance rejection control[J].
IEEE Transactions on Industrial Electronics , 2009, 56 (3) : 900-906 DOI:10.1109/TIE.2008.2011621 ( 0) 0)
|
| [12] |
XUE W C, BAI W Y, YANG S, et al. ADRC with adaptive extended state observer and its application to air-fuel ratio control in gasoline engines[J].
IEEE Trans. on Industrial Electronics , 2015, 62 (9) : 5847-5857 DOI:10.1109/TIE.2015.2435004 ( 0) 0)
|
| [13] |
周风余, 单金明, 王伟, 等. 基于ADRC的船舶航向控制器设计与仿真研究[J].
山东大学学报(工学版) , 2009, 39 (1) : 57-62-76 ZHOU Fengyu, SHAN Jinming, WANG Wei, et al. Research on the design and simulation of a ship course controller based on ADRC[J]. Journal of Shandong University (Engineering Science) , 2009, 39 (1) : 57-62-76 (  0) 0)
|
| [14] |
刘文江, 隋青美, 周风余. 基于自抗扰控制技术的船舶直线航迹控制器设计[J].
山东大学学报(工学版) , 2010, 40 (6) : 48-53 LIU Wenjiang, SUI Qingmei, ZHOU Fengyu. Straight-line tracking control of ships based on ADRC[J]. Journal of Shandong University (Engineering Science) , 2010, 40 (6) : 48-53 (  0) 0)
|
| [15] |
胡坤, 张孝芳, 刘常波. 基于遗传算法的无人水下航行器深度自抗扰控制[J].
兵工学报 , 2013, 34 (2) : 217-222 HU Kun, ZHANG Xiaofang, LIU Changbo. Unmanned underwater vehicle depth ADRC based on genetic algorithm near surface[J]. Acta Armamentarii , 2013, 34 (2) : 217-222 (  0) 0)
|
| [16] |
潘为刚, 李贻斌. 优化自抗扰控制器在船舶主机上的应用与仿真研究[J].
内燃机工程 , 2012, 33 (5) : 74-78 PAN Weigang, LI Yibin. Application and simulation research of optimal active disturbance rejection controller in marine main engine[J]. Chinese Internal Combustion Engine Engineering , 2012, 33 (5) : 74-78 (  0) 0)
|
| [17] |
王瑞琪, 张承慧, 李珂. 基于改进混沌优化的多目标遗传算法[J].
控制与决策 , 2011, 26 (9) : 1391-1397 WANG Ruiqi, ZHANG Chenghui, LI Ke. Multi-objective genetic algorithm based on improved chaotic optimization[J]. Control and Decision , 2011, 26 (9) : 1391-1397 (  0) 0)
|
| [18] |
PARK T, CHOE R, RYU K. Dual-population genetic algorithm for nonstationary optimization[C]// Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation. Atlanta, U S A: Association for Computing Machinery, 2008: 1025-1032.
http://cn.bing.com/academic/profile?id=2247322445&encoded=0&v=paper_preview&mkt=zh-cn ( 0) 0)
|
| [19] |
ESSAFI I, MATI Y, DAUZÈRE-PÉRÈS S. A genetic local search algorithm for minimizing total weighted tardiness in the Job-Shop scheduling problem[J].
Computers & Operations Research , 2008, 35 (8) : 2599-2616 ( 0) 0)
|
| [20] |
DO K, PAN J. Global robust adaptive path following of underactuated ships[J].
Automatica , 2006, 42 (10) : 1713-1722 DOI:10.1016/j.automatica.2006.04.026 ( 0) 0)
|
| [21] |
FOSSEN T, BREIVIK M, SKJETNE R. Line-of-sight path following of underactuated marine craft[C]// Proceedings of the 6th IFAC MCMC. Oxford, UK: IFAC Elsevier Ltd, 2003: 244-249.
( 0) 0)
|
| [22] |
BREIVIK M, HOVESTEIN V, FOSSEN T. Staight line target tracking for unmanned surface vehicles[J].
Modeling, Identification and Control , 2008, 29 (4) : 131-149 DOI:10.4173/mic.2008.4.2 ( 0) 0)
|
| [23] |
PEYMANI E, FOSSEN T. Path following of underwater robots using Lagrange multipliers[J].
Robotics and Autonomous Systems , 2015, 67 : 44-52 DOI:10.1016/j.robot.2014.10.011 ( 0) 0)
|
| [24] |
赵志良.非线性自抗扰控制器的收敛性[D].北京:中国科学技术大学, 2012.
ZHAO Zhiliang. Convergence of nonlinear active disturbance rejection control[D]. Beijing: University of Science and Technology of China, 2012. http://cdmd.cnki.com.cn/article/cdmd-10358-1012503631.htm (  0) 0)
|
| [25] |
PARK T, RYU K. A dual-population genetic algorithm for adaptive diversity control[J].
IEEE Transactions on Evolutionary Computation , 2010, 14 (6) : 865-884 DOI:10.1109/TEVC.2010.2043362 ( 0) 0)
|



