2. 湖北省磁悬浮轴承工程技术研究中心, 湖北 武汉 430070
2. Hubei Magnetic Suspension Engineering Technology Research Center, Wuhan 430070, Hubei, China
磁悬浮轴承也称为电磁轴承或磁力轴承, 是典型的机电一体化系统[1], 以无摩擦、无磨损、无需润滑、低耗能、高精度等优点已被广泛应用于机械加工、透平机械、医疗设备、航空航天、真空技术等领域[2]。磁悬浮轴承提供电磁力支承转子, 但若其某个环节发生故障, 将会导致转子失控, 造成严重影响[3]。执行器故障是磁悬浮轴承系统中的常见故障之一, 一般认为其主要是由于线圈断路或绝缘失效引起的短路造成的, 而后者是更常见的原因, 将导致电流控制异常, 无法产生正常的电磁力。针对这一故障, 目前大多数的研究是进行容错控制, 如对磁悬浮轴承进行冗余支承结构的重构[4-5]已取得了一定进展。
准确有效的故障诊断, 是容错控制的实现前提。文献[6]利用了振动法来分析变压器箱体内部的线圈、铁芯的松动状况; 文献[7]采用了励磁电流判别法, 在发电机饱和的情况下, 得到了与理论相吻合的结论; 文献[8]提出了一种基于模型的多故障识别方法, 运用频域中的最小二乘拟合法分析了不同的故障模型; 文献[9]和[10]主要研究了小波分析在磁力轴承系统故障中的应用; 文献[11]通过高斯广义似然比检测(generalized likelihood ratio testd, GLRT)来获取变化的平均值, 进而检测电磁线圈的故障; 文献[12]通过对主动磁轴承中控制电流频率等特性的分析, 提供了一种检测不平衡故障的方法。文献[13]提出了一种新的全系统故障诊断算法, 利用状态估计器和参数估计器进行检测, 识别和分析执行器故障。
但值得注意的是, 磁悬浮轴承系统由于电磁线圈绝缘失效, 导致线圈常数变化, 但电流总体可控。因此, 文献[14]通过比较线圈实际电流与设定电流, 采用了一种基于阈值的故障检测方法。在一定时期内, 电流实际值与设定值之间任何比较大的差异都直接指示了执行器线圈出现了故障, 但难点在于难以找到切实有效的阈值。本研究提出一种在线电磁线圈故障检测方法, 应用于磁悬浮轴承, 基于调制周期内电流变化特性来判别电磁线圈的线圈常数, 对线圈绝缘损坏有较好的检测效果。本研究所提出的方法为电磁线圈的故障检测提供来了一种新的思路, 对进一步设计针对磁悬浮轴承的容错控制器, 实现转子在部分执行器失效时的有效支承具有意义。
1 开关功放在两态调制下的基本原理如图 1所示, 整个的磁悬浮轴承控制系统是由位置环和电流环构成的双闭环控制系统。位置环控制器根据转子位置误差输出控制量; 电流环则根据位置环的输出控制量指令, 产生期望电磁线圈电流, 继而产生期望电磁力, 以维持转子稳定。其中, 电流环在开关功放中实现, 如图 1中的虚线框。依赖电流负反馈环路, 电流控制器输出控制逻辑, 来驱动功率主电路, 实现受控电流输出。
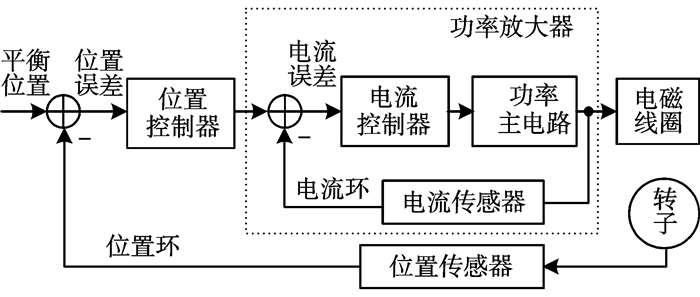
|
图 1 磁悬浮轴承控制系统结构 Figure 1 The structure of Magnetic suspension bearingcontrol system |
开关功放桥路的搭建需要考虑是否需要变换电流的方向, 通常来讲, 只需要正向的电流输出, 因此功率主电路采用半桥结构。功放通过控制半桥电路的开关元件VT1和VT2的开合将母线电压加到线圈两端, 为线圈供电。在两态调制模式下, 功放仅存在充电和放电两种状态, 当VT1和VT2同时打开, 母线电源向负载线圈充电, 线圈电流上升, 此时为充电状态; 当VT1和VT2同时关闭, 线圈通过续流二极管D1和D2构成回路, 将能量回馈给母线电源, 线圈中的电流下降, 此时为放电状态, 如图 2所示。
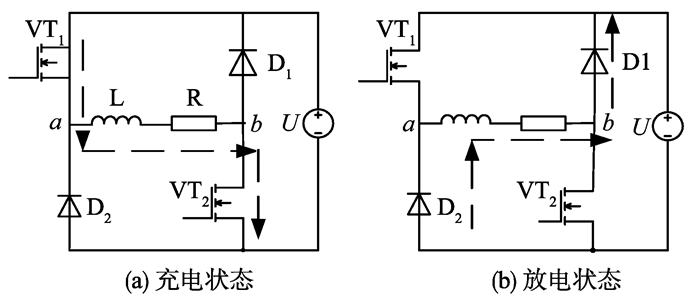
|
图 2 两态调制下的电流变化 Figure 2 The current flows under bi-state modulation |
根据图 2(a), 充电时, 功率器件VT1和VT2导通, 母线电源向负载线圈充电, 可得电路微分方程为
| $ U = L\frac{{{\rm{d}}i\left( t \right)}}{{{\rm{d}}t}} + Ri\left( t \right) + 2{U_{\rm{s}}}, $ | (1) |
式中:U为母线电压, Us为开关管导通压降, L为线圈电感, R为线圈电阻, i为通过线圈的电流。
对式(1)进行微分方程求解可得
| $ i\left( t \right) = \frac{{U - 2{U_{\rm{s}}}}}{R}\left( {1 - {{\rm{e}}^{ - \frac{t}{\tau }}}} \right) + {i_0}{{\rm{e}}^{ - \frac{t}{\tau }}}, $ | (2) |
进一步对电流求导, 得电流变化率
| $ {k_1} = \frac{{{\rm{d}}i\left( t \right)}}{{{\rm{d}}t}} = \frac{{U - 2{U_{\rm{s}}}}}{L}{{\rm{e}}^{ - \frac{t}{\tau }}} - \frac{{{i_0}}}{\tau }{{\rm{e}}^{ - \frac{t}{\tau }}}, $ | (3) |
式(2)和(3)中:i0为磁轴承线圈中的初始电流, τ=L/R为磁轴承线圈的时间常数。
由于τ远远大于开关周期, 因此式(2)的指数部分可以近似用线性函数代替, 电流近似为直线上升, 在这种状态下, 母线电压向线圈输入能量, 电流变化率k1的表达式近似为
| $ {k_1} = \frac{{U - 2{U_{\rm{s}}}}}{L} - \frac{{{i_0}}}{\tau }。$ | (4) |
根据图 2(b), 放电时, 功率器件VT1和VT2同时关闭, 线圈与两个二极管以及电源构成回路, 线圈中的电流下降, 根据电路关系, 此时的电路微分方程为
| $ - U = L\frac{{{\rm{d}}i\left( t \right)}}{{{\rm{d}}t}} + Ri\left( t \right) + 2{U_{\rm{d}}}, $ | (5) |
式中Ud为续流二极管导通压降。
对式(5)进行微分方程求解可得
| $ i\left( t \right) = - \frac{{U + 2{U_{\rm{d}}}}}{R}\left( {1 - {{\rm{e}}^{ - \frac{t}{\tau }}}} \right) + {i_0}{{\rm{e}}^{ - \frac{t}{\tau }}}。$ | (6) |
对电流求导, 得电流变化率k2的表达式为
| $ {k_2} = \frac{{{\rm{d}}i\left( t \right)}}{{{\rm{d}}t}} = - \frac{{U + 2{U_{\rm{d}}}}}{L}{{\rm{e}}^{ - \frac{t}{\tau }}} - \frac{{{i_0}}}{\tau }{{\rm{e}}^{ - \frac{t}{\tau }}}。$ | (7) |
对式(6)和(7)进行近似线性化处理, 电流近似直线下降, 此时电磁线圈向母线电压回馈能量[15-17], 电流变化率k2的表达式近似为
| $ {k_2} = - \frac{{U + 2{U_{\rm{d}}}}}{L} - \frac{{{i_0}}}{\tau }。$ | (8) |
根据前文分析, 在两态调制下, 线圈在一个开关周期内的输出电流变化如图 3所示[18-19]。
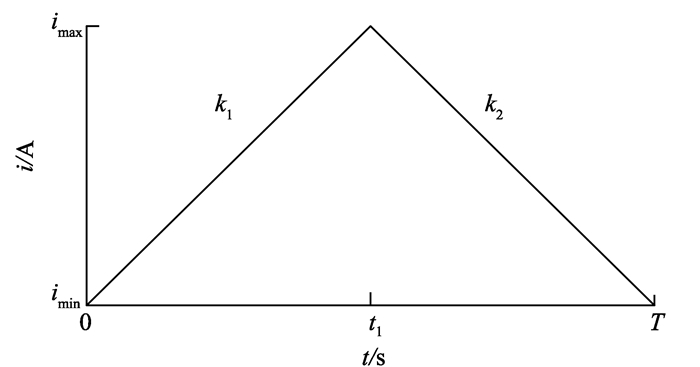
|
图 3 两态调制下的输出电流变化波形 Figure 3 The change waveform of the output current under bi-state modulation 注: imin—稳态时的最小电流; imax—稳态时的最大电流; T—开关周期; t1—电流上升时间。 |
由图 3可得
| $ {i_{ab}} = \left\{ \begin{array}{l} {k_1}t + {i_{\min }},nT \le t \le nT + {t_1}\\ {k_2}t + {i_{\max }},nT + {t_1} \le t \le \left( {n + 1} \right)T \end{array} \right.。$ | (9) |
由于Us和Ud远远小于母线电压U, 可忽略。分析可知, 影响k1和k2的主要因素是母线电压U、线圈的电感L和电阻R。因此, 在母线电压U正常的情况下, 一旦线圈发生了断路、局部短路等故障时, 就会影响线圈的电感L和电阻R, 进而使k1和k2超出其应有的数值范围。通过检测电流变化率即可快速检测出线圈是否发生故障, 从理论上证明了本研究方法是可行的。
3 两态调制下输出电流模型对于图 3的电流变化, 忽略掉开关管导通压降Us和续流二极管导通压降Ud, 电流上升阶段, 线圈两端的电压Uab约等于U; 电流下降阶段, Uab约等于-U, 即
| $ {U_{ab}} = \left\{ \begin{array}{l} + U,nT \le t \le nT + {t_1}\\ - U,nT + {t_1} \le t \le \left( {n + 1} \right)T \end{array} \right., $ | (10) |
其中,
| $ {t_1} = T{U_{\rm{f}}}/{U_{\rm{t}}}, $ | (11) |
Uf是脉冲宽度调制(pulse width modulation, PWM)发生器输入的调制信号, Ut是三角载波单边幅值, T为开关周期, nT为第n个开关周期。
在[nT, (n+1)T]时间内对线圈两端的电压Uab进行傅里叶级数展开[20-21], 得
| $ {U_{ab}} = \frac{{{a_0}}}{2} + \sum\limits_{k = 1}^\infty {{a_k}\cos \left( {k\omega t} \right)} + \sum\limits_{k = 1}^\infty {{b_k}\sin \left( {k\omega t} \right)} , $ | (12) |
式中:a0为直流分量; ak为余弦函数分量的幅值; bk为正弦函数分量的幅值; k为谐波次数, k=1, 2, …。
a0, ak和bk的表达式分别为:
| $ {a_0} = \frac{2}{T}\int_{nT}^{\left( {n + 1} \right)T} {{U_{ab}}{\rm{d}}t} = \left( {4\frac{{{U_{\rm{f}}}}}{{{U_{\rm{t}}}}} - 2} \right)U, $ | (13) |
| $ {a_k} = \frac{2}{T}\int_{nT}^{\left( {n + 1} \right)T} {{U_{ab}}{\rm{cos}}\left( {k\omega t} \right){\rm{d}}t} = \frac{{2U}}{{k{\rm{ \mathsf{ π} }}}}\sin \left( {2k{\rm{ \mathsf{ π} }}\frac{{{U_{\rm{f}}}}}{{{U_{\rm{t}}}}}} \right), $ | (14) |
| $ \begin{array}{*{20}{c}} {{b_k} = \frac{2}{T}\int_{nT}^{\left( {n + 1} \right)T} {{U_{ab}}{\rm{sin}}\left( {k\omega t} \right){\rm{d}}t} = }\\ {\frac{{2U}}{{k{\rm{ \mathsf{ π} }}}}\left[ {1 - \cos \left( {2k{\rm{ \mathsf{ π} }}\frac{{{U_{\rm{f}}}}}{{{U_{\rm{t}}}}}} \right)} \right]。} \end{array} $ | (15) |
将式(13)至(15)代入到式(12)中, 可得
| $ \begin{array}{l} {U_{ab}} = \left( {2\frac{{{U_{\rm{f}}}}}{{{U_{\rm{t}}}}} - 1} \right)U + \\ \;\;\;\;\;\;\;\sum\limits_{k = 1}^\infty {\frac{{2U}}{{k{\rm{ \mathsf{ π} }}}}\left[ {\sin \left( {2k{\rm{ \mathsf{ π} }}\frac{{{U_{\rm{f}}}}}{{{U_{\rm{t}}}}} - k\omega t} \right) + \sin \left( {k\omega t} \right)} \right]} 。\end{array} $ | (16) |
通过线圈的电流iab与线圈两端的电压Uab的关系满足
| $ \frac{{{i_{ab}}}}{{{U_{ab}}}} = \frac{1}{{R + Ls}}。$ | (17) |
由式(16)和(17)建立两态调制下的开关功放的Matlab/Simulink仿真模型, 如图 4所示。
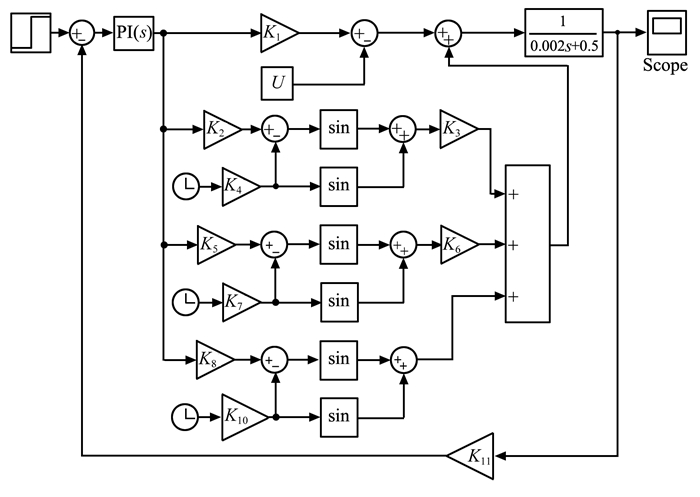
|
图 4 两态调制下的输出电流仿真模型 Figure 4 The simulation model of output current underbi-state modulation |
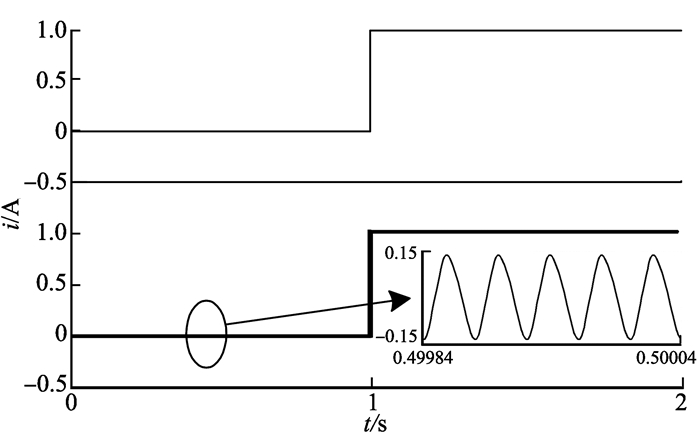
仿真条件:开关频率为25 kHz, 即一个开关周期为40 μs, 母线电压30 V, 线圈的电阻0.5 Ω, 电感2 mH, 比例积分微分(proportion integration derivative, PID)控制器的参数选择为:Kp=40, Ki=30, Kd=0。采用阶跃信号激励, 电流阶跃幅值为1 A, 仿真时的电流波形如图 5所示。可以发现,输出电流的波形能正常的跟随激励信号, 在充电过程, 电流波形近似直线上升, 电流变化率基本保持不变; 在放电过程, 电流波形近似直线下降, 电流变化率也基本保持不变, 与前面理论分析保持一致。
|
图 5 阶跃信号激励下的仿真波形 Figure 5 The simulation waveform excited by step signal 注:上半部分是激励信号的波形图; 下半部分是输出电流的波形图。 |
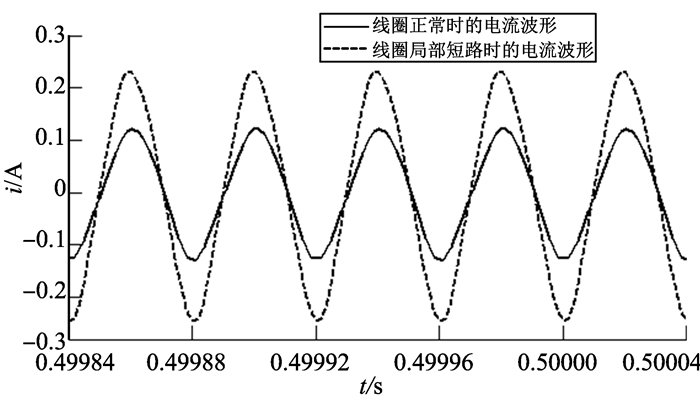
当线圈发生了局部短路时, 线圈常数会发生变化, 在保证其他的参数不变的情况下, 此时为了模拟线圈故障, 假设线圈的电阻由0.5 Ω变为0.2 Ω, 电感由2 mH变为了1 mH, 仿真时的电流变化波形对比如图 6所示。
|
图 6 线圈局部短路时的仿真对比 Figure 6 The simulation comparison of local short circuit of coil |
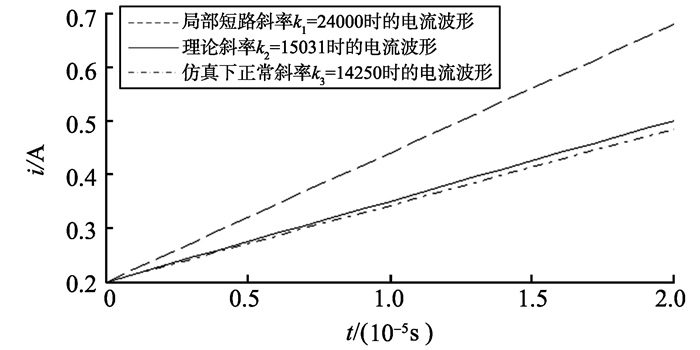
图 6中, 虚线部分为线圈发生局部短路时的电流波形, 可以发现, 电流纹波明显增大, 而开关周期保持不变, 所以电流变化斜率与正常线圈相比, 明显增大。以充电过程为例, 将仿真的具体数据代入式(4)可以得到仿真时的理论斜率, 并可以根据图 6的电流变化波形, 获得在仿真过程中正常和局部短路时的实际的电流变化率。则电流在一个调制周期内的理论斜率、仿真时的正常斜率以及模拟局部短路的斜率对比如图 7所示。
|
图 7 充电过程中的理论斜率、仿真正常斜率以及局部短路的斜率对比 Figure 7 The comparison of theoretical slope, simulation slope and short circuit slope in the charging process |
由图 7可知, 仿真时的正常斜率与理论斜率相差不大, 但发生局部短路时的电流变化率明显增大, 因此通过检测电流变化率的值即可进行线圈故障检测, 仿真结果有效地证明了本研究方法的可行性。
4 采样系统配置 4.1 电流反馈电路电流反馈回路是保障功放稳定的基础, 以DSP为主控芯片的电流反馈回路如图 8所示。图中反馈环节由电流传感器、隔离电路、滤波电路、调理电路、模数转换器(analog-to-digital converter, ADC)构成。由于电流信号不能够直接被采集, 通常需要通过电流传感器进行比例衰减, 再经过采样电阻转换成电压信号, 经过隔离、滤波、调理等电路转换成与参考信号同一级别的电压信号。反馈环节有两个作用:一个作用是在反馈回路中, 将电流信号转换成与参考信号同一级别的电压信号, 以便与参考信号做差, 然后进行离散PID运算以及获得PWM占空比等; 另一个作用则是采样得到电压数字量, 进而在编程环境中经过相关算法计算出电流变化率。

|
图 8 电流反馈回路 Figure 8 The current feedback loop |
由于试验中功放的开关频率为25 kHz, 为了使采样点的数量能够比较好地反映出电流变化斜率, ADC的采样频率采用450 kHz, 即一个周期内采样19个离散点; 采用12位的ADC进行量化, 满量程数字量为4 096, 采用内部3 V作为参考电压, ADC采样到的电压数字量表达式为
| $ a = \frac{{4096{U_{\rm{c}}}}}{{{U_{{\rm{ref}}}}}}, $ | (18) |
式中:a是采样到的电压数字量, Uc是待采样电压, Uref是参考电压, 这里即为3 V。得到了电压的数字量后, 便可在相关的软件环境下进行算法编程, 获得电流变化率的值。
4.2 电流变化率求解算法由于实际过程中不可避免的会受到噪声等干扰的影响, 会导致采样结果中存在明显较大的干扰信号, 因此首先通过编程对采样结果进行数字滤波处理, 滤掉干扰值。在一个开关周期内, 设当前采样到的电压数字量为an, 下一个采样值为an+1, 其中n=1, 2, …, 18, 则此刻线圈的输出电流变化率的算法表达式为
| $ {k_n} = \frac{{{G_{\rm{f}}}\left( {{a_{n + 1}} - {a_n}} \right){U_{{\rm{ref}}}}}}{{4096{R_{\rm{a}}}{T_n}}}, $ | (19) |
式中:Gf是电流传感器的比例衰减系数, 本研究中为250;Ra是采样电阻, 为250 Ω; Tn是ADC的采样周期。
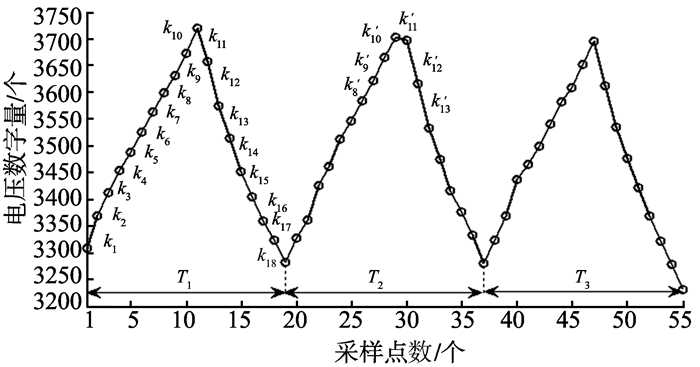
实际中采样到的连续三个开关周期内的离散点如图 9所示, 并按照式(19), 以充电过程中为例, 得到了一系列kn。
|
图 9 三个开关周期内采样到的离散点 Figure 9 The discrete points sampled in three switching cycles |
根据功放在两电平调制下的原理可知, 若前后两个采样点分布在充电和放电之间的拐点两侧时, 则由式(19)则得到的结果值并不是正确的kn, 如图 9中T2周期内的k11'。考虑到这一点, 在实际的编程算法中对kn进行了判断确认。根据实际逻辑关系, 以连续3次斜率都大于0, 则中间一次作为充电过程中的电流变化率; 连续3次斜率都小于0, 则中间一次的作为放电过程中的电流变化率。既消除了拐点的影响, 又很好地得到了电流变化率。
为了使结果更加准确, 又不影响检测出故障所需的时间, 将每个周期充电和放电过程中的电流变化率kn分别求和后, 再进行取平均值运算, 得到了误差更小的斜率k, 用于判断是否发生故障。同样以充电过程为例, 图 10是在线圈正常时, 经过大量采样后, 得到的连续的2 000组k的统计结果图。
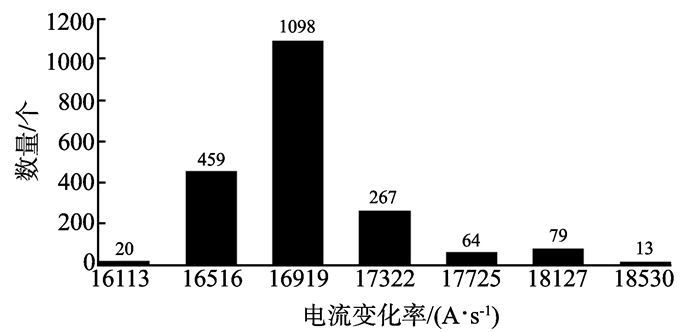
|
图 10 充电过程中连续2 000组k的统计柱状图 Figure 10 The statistical histogram of 2 000 consecutivegroups of k in the charging process |
根据图 10, 充电过程中k的正常范围为:16 113≤k≤18 530。而根据式(4), 代入试验的具体数值:母线电压30 V, 线圈的电感1.75 mH, 电阻0.5 Ω, 以及充电过程中的i0为0.2 A, 得到的理论斜率值为17 086。斜率对比如图 11所示。

|
图 11 充电过程中的k对比 Figure 11 The contrast diagram for k in the charging process |
由于试验过程中不可避免存在误差, 以及转子在正常运转时, 并不是完全悬浮在理想位置, 导致磁极与转子间的气隙存在上下波动而引起了线圈电感的变化, 最终导致了实际的k与理论上的斜率有一定的偏差, 但是误差在允许的范围内。因此, 为了提高故障检测的灵敏度, 在编程算法中将实际k的范围定为线圈正常时的斜率范围, 即16 113≤k≤18 530, 整个算法的程序流程如图 12所示。
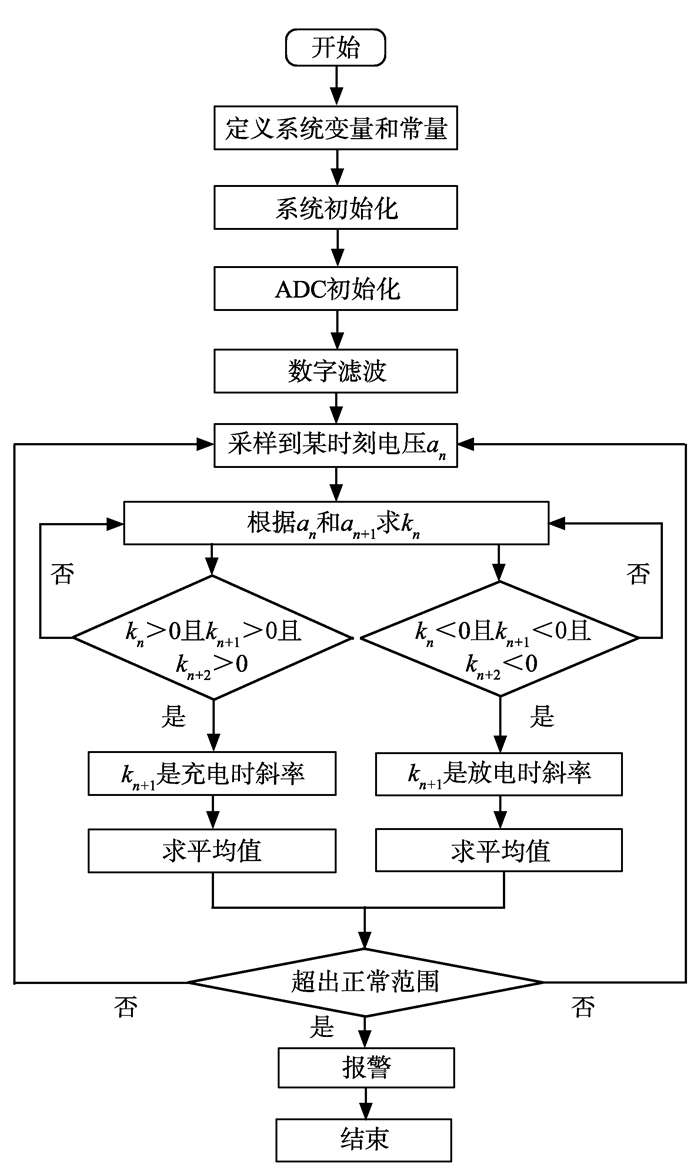
|
图 12 电流变化率算法的程序流程图 Figure 12 The program flow chart of algorithm forcurrent change rate |
搭建的试验平台如图 13所示, 自行研制了基于TMS320F28335的DSP电流控制器板, 基于绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT)的功率桥电路。采用合众达公司的Seed 510仿真开发平台, 并采用信号发生器产生激励信号, 采用Agilent公司的四通道数字示波器观测输出电流信号, 采用可控稳压直流电源提供母线电压。

|
图 13 试验平台 Figure 13 The test platform |
本研究算法程序的运行周期大约为2 ms, 根据线圈故障可能发生在采样过程中的不同时刻, 按照此程序的逻辑关系, 在不超过两个程序周期内, 即4 ms的时间内, 就可以检测出线圈故障。
(1) 线圈断路
当线圈发生断路故障, 此时, 从示波器中读出的输出电流的波形如图 14所示。
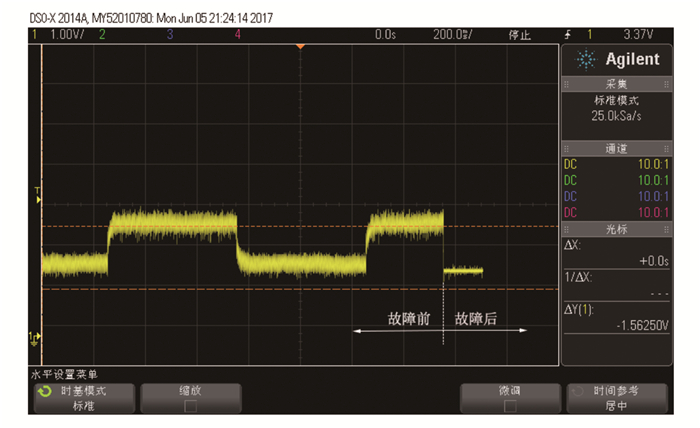
|
图 14 线圈发生断路时的电流波形 Figure 14 The current waveform of a coil when a circuit is broken |
以充电过程为例进行分析, 此时测得断路故障时的的电流变化率与正常范围的对比如图 15所示。
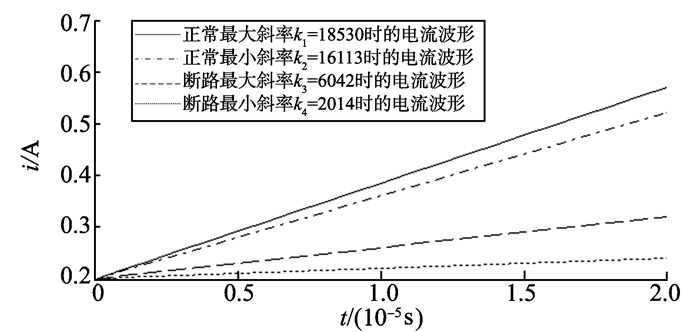
|
图 15 断路时的斜率对比 Figure 15 The slope contrast when a circuit is broken |
可以发现, 线圈发生断路故障时, 电流变化率的值明显变小, 远远超出了正常范围。此时通过示波器检测出故障所需的时间如图 16所示(其中上面红色部分为所设置的DSP芯片的一个输出引脚的电位变化波形, 下面黄色部分为实际的输出电流波形)。故障发生瞬间至引脚电位变为低电平瞬间这段时间即为故障检测时间, 由图可知, 诊断时间约2 ms。
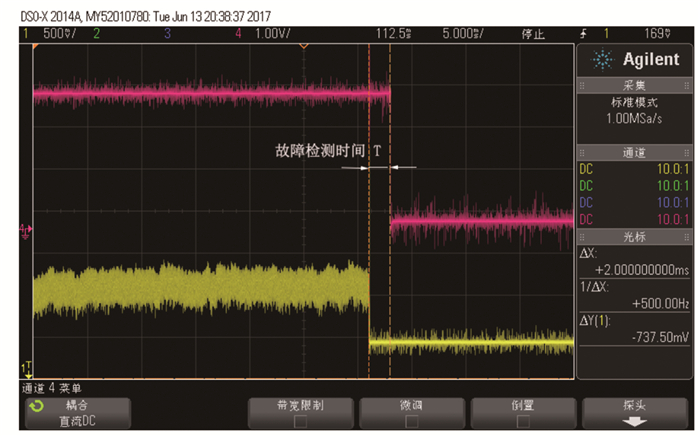
|
图 16 断路时的故障检测时间 Figure 16 The fault detection time when a circuit is broken |
(2) 线圈局部短路
当线圈发生局部短路故障, 此时从示波器得到的输出电流波形如图 17所示。

|
图 17 线圈发生局部短路时的电流波形 Figure 17 The current waveform of a coil with a local short circuit |
可以看出, 线圈发生了局部短路故障, 电流纹波明显变大, 同样以充电过程为例, 此时测得的电流变化率与正常范围的对比如图 18所示。
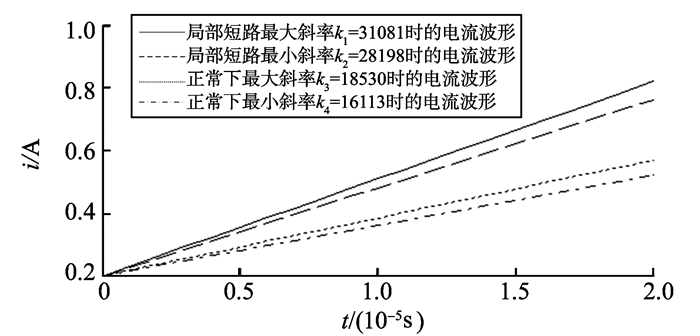
|
图 18 局部短路时的斜率对比 Figure 18 The slope contrast for local short circuit |
由图 18可知, 线圈发生了局部短路, 电流变化率明显增大, 大大超出了正常的斜率范围。此时通过示波器获得的故障检测时间如图 19所示。可以发现, 在这种情况下, 只需要大约1.2 ms, 就可以快速地检测出线圈发生了故障。
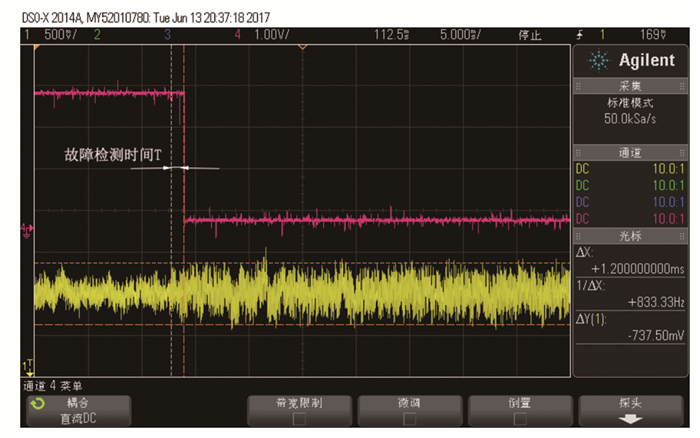
|
图 19 局部短路时的故障检测时间 Figure 19 The fault detection time for local short circuit |
对于局部短路的情况, 进一步通过试验来检验故障诊断的灵敏度, 即当线圈发生局部短路时, 电感变化多大范围, 故障诊断系统才能检测出。同样以充电过程为例, 根据实际的电流变化率的范围16 112到18 530, 再结合式(4)可得, 发生局部短路时, 若电感为1.62~1.75 mH时, 此时是检测不出故障的。因此试验通过检测一个超出该范围的电感1.6 mH的电流变化率, 来检验故障诊断的灵敏度。图 20是线圈局部短路后, 电感变化为1.6 mH的充电过程斜率对比图。
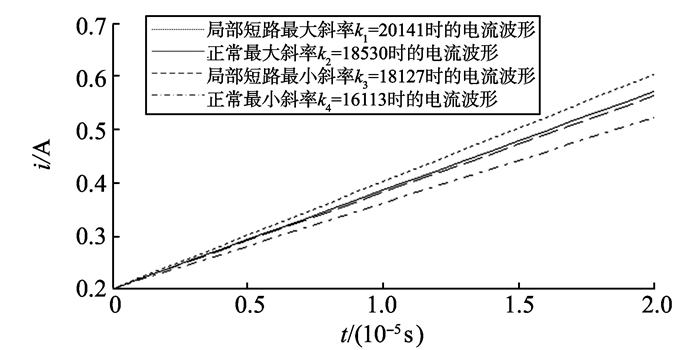
|
图 20 短路后电感为1.6 mH的斜率对比 Figure 20 The slope contrast when the inductor turns to1.6 mH after short circuit |
可见, 发生局部短路时, 当电感变为1.6 mH时, 其斜率最大值超出了正常的斜率范围, 此时检测出了故障。
6 结论本研究建立了两态调制模式下的数字开关功放的等效数学模型, 进行了相关理论分析; 搭建了Matlab/Simulink仿真模型和试验平台, 进行了仿真与试验研究, 可得结论如下:
(1) 本研究所讨论的方法基于电流变化特性, 只要在线圈的等效电感短路超过阈值, 即可检测出线圈绝缘失效引起的(局部)短路故障。试验结果证明了本研究所讨论方法的可靠性。
(2) 本研究所提出的检测算法执行周期大约2 ms, 一般需要两个执行周期即可判别线圈故障, 具备较好的实时性。本研究为线圈故障的在线检测提供了一种新的思路, 对进一步进行磁悬浮轴承容错控制及故障补偿等具有一定的意义。
| [1] | SCHWEITZER G, BLEULER H, TRAXLER A. Active magnetic bearings: basics, properties and applications of active magnetc bearings[M]. Zurich, Swizerland: vdf Hochschulverlag AG an der ETH Zurich, 1994. |
| [2] | SCHWEITZER G, MASLEN E H. Magnetic bearings: theory, design, and application to rotating machinery[M]. Berlin, Germany: Springer, 2009. |
| [3] | MASLEN E H, MEEKER D C. Fault tolerance of magnetic bearings by generalized bias current linearization[J]. IEEE Transactions on Magnetics, 1995, 31(3): 2304-2314 DOI:10.1109/20.376229 |
| [4] | CHENG X, LIU H, SONG S, et al. Reconfiguration of tightly-coupled redundant supporting structure in active magnetic bearings under the failures of electromagnetic actuators[J]. International Journal of Applied Electromagnetics & Mechanics, 2017, 54(3): 1-12 |
| [5] | CHENG X, CHEN Q, ZENG H, et al. Reconfiguration rules for loosely-coupled redundant supporting structure in radial magnetic bearings[J]. International Journal of Applied Electromagnetics & Mechanics, 2016, 51(2): 91-106 |
| [6] |
汲胜昌, 刘味果, 李彦明, 等. 振动法用于在线监测电力变压器绕组及铁心状况的可行性研究[J].
高压电器, 2001, 37(5): 4-7 JI Shengchang, LIU Weiguo, LI Yanming, et al. Feasibility of vibration analysis method in application to on-line monitoring of the core and the winding of power transformer[J]. High Voltage Apparatus, 2001, 37(5): 4-7 DOI:10.3969/j.issn.1001-1609.2001.05.002 |
| [7] |
李永刚, 李和明, 赵华. 汽轮发电机转子绕组匝间短路故障诊断新判据[J].
中国电机工程学报, 2003, 23(6): 112-116 LI Yonggang, LI Heming, ZHAO Hua. The new criterion on interturn short-circuit fault diagnose of steam turbine generator rotor windings[J]. Proceedings of the CSEE, 2003, 23(6): 112-116 DOI:10.3321/j.issn:0258-8013.2003.06.022 |
| [8] | BACHSCHMID N, PENNACCHI P, VANIA A. Identification of multiple faults in rotor systems[J]. Journal of Sound & Vibration, 2002, 254(2): 327-366 |
| [9] | CADE I S, KEOGH P S, SAHINKAYA M N. Fault identification in rotor/magnetic bearing systems using discrete time wavelet coefficients[J]. IEEE/ASME Transactions on Mechatronics, 2005, 10(6): 648-657 DOI:10.1109/TMECH.2005.859834 |
| [10] |
陈小玄, 罗大庸, 单勇腾. 小波分析在转子绕组匝间短路故障诊断中的应用[J].
电机与控制学报, 2007, 11(2): 143-147 CHEN Xiaoxuan, LUO Dayong, SHAN Yongteng. Application of wavelet analysis on fault diagnosis of interturn short circuit in rotor winding[J]. Electric Machines & Control, 2007, 11(2): 143-147 DOI:10.3969/j.issn.1007-449X.2007.02.011 |
| [11] | NAGEL L, GALEAZZI R, VOIGT A J, et al. Fault diagnosis of active magnetic bearings based on Gaussian GLRT detector[C]// Proceedings of the 3rd Control and Fault-Tolerant Systems. New York, USA: IEEE, 2016: 540-547. |
| [12] | DOHNAL F, SEKHAR A S. Current signature analysis for unbalance fault detection in a rotor supported by active magnetic bearings[J]. International Journal of Condition Monitoring, 2014, 4(1): 2-8 DOI:10.1784/204764214813883315 |
| [13] | TSAI N C, KING Y H, LEE R M. Fault diagnosis for magnetic bearing systems[J]. Mechanical Systems & Signal Processing, 2009, 23(4): 1339-1351 |
| [14] | LOESCH F. Detection and correction of actuator and sensor faults in active magnetic bearing system[C]//Proceedings of the 8th International Symposium on Magnetic Bearing. Zurich, Switzerland: vdf Hochschulverlag AG an der ETH Zurich, 2002: 113-118. |
| [15] |
常肖, 徐龙祥, 董继勇. 磁悬浮轴承数字功率放大器[J].
机械工程学报, 2010, 46(20): 9-14 CHANG Xiao, XU Longxiang, DONG Jiyong. Digital power amplifier of active magnetic bearing[J]. Journal of Mechanical Engineering, 2010, 46(20): 9-14 |
| [16] | WANG J, XU L. System model of three-level switching power amplifier for magnetic bearing[C]// International Conference on Measuring Technology and Mechatronics Automation. New York, USA: IEEE Computer Society, 2009: 708-711. |
| [17] |
臧晓敏, 王晓琳, 仇志坚, 等. 磁轴承开关功放中电流三态调制技术的研究[J].
中国电机工程学报, 2004, 24(9): 167-172 ZANG Xiaomin, WANG Xiaolin, QIU Zhijian, et al. Research on current modetri-state modulation technology in switching power amplifier for magnetic bearing[J]. Proceedings of the CSEE, 2004, 24(9): 167-172 DOI:10.3321/j.issn:0258-8013.2004.09.029 |
| [18] |
程鑫, 曾红勇, 吴华春, 等. 磁悬浮开关功放数学模型与控制实现[J].
华中科技大学学报(自然科学版), 2015(Suppl. 1): 493-496 CHENG Xin, ZENG Hongyong, WU Huachun, et al. Mathematical model and control implementation of switching power amplifier in magnetical-levitated system[J]. Journal of Huazhong University of Science & Technology (Natural Science Edition), 2015(Suppl. 1): 493-496 |
| [19] | CHENG X, WANG B, CHEN Q, et al. A unified design and the current ripple characteristic analysis of digital switching power amplifier in active magnetic-levitated bearings[J]. International Journal of Applied Electromagnetics & Mechanics, 2017, 55(3): 391-407 |
| [20] |
王军, 徐龙祥. 磁悬浮轴承开关功率放大器等效数学模型[J].
电工技术学报, 2010, 25(4): 54-58 WANG Jun, XU Longxiang. Equivalent mathematical model of switched power amplifier for magnetic bearings[J]. Journal of electrical technology, 2010, 25(4): 54-58 |
| [21] |
张亮, 房建成. 基于MATLAB的电磁轴承开关功放建模与仿真研究[J].
系统仿真学报, 2007, 19(11): 2395-2398 ZHANG Liang, FANG Jiancheng. Research on modeling and Simulation of switching power amplifier for active magnetic bearing applications based on MATLAB[J]. Journal of System Simulation, 2007, 19(11): 2395-2398 DOI:10.3969/j.issn.1004-731X.2007.11.001 |



