2. 湖北省磁悬浮工程技术中心, 湖北 武汉 430070
2. Hubei Provincial Engineering Technology Research Center for Magnetic Suspension, Wuhan 430070, Hubei, China
隔振是振动工程领域的一个重要分支, 按照振动控制的机理可分被动隔振和主动隔振[1-3]。被动隔振主要削减高频振动(一般10 Hz以上), 对低于10 Hz的低频振动抑制不明显。主动隔振又称有源隔振, 能够有效改善传统被动隔振在低频段的性能。主动隔振的研究主要有结构设计、配置方式、控制策略和控制算法等方面, 而作动器[4-5]是主动隔振中的关键器件, 其性能直接影响到主动隔振效果。
磁悬浮作动器作为一种电磁式作动器, 利用电磁产生磁力, 具有频响范围宽、响应快、无接触等优点[6-9]。但它是一个开环不稳定系统, 需对其进行控制。传统的PID控制器结构相对简单, 系统各项参数均有其物理意义, 应用到实际工程更加方便。随着控制理论的不断发展, 基于磁悬浮作动器多变量、非线性等特性, 传统PID控制器无法满足控制要求[10-12],而串级PID控制方法可以通过减小副回路闭环系统的相位滞后和等效时间常数来提高系统稳定性和响应速度, 通过副回路控制器增益增加串级控制系统有阻尼频率来改善系统的控制质量[13]。
为此, 本研究提出将串级PID控制应用在磁悬浮作动器的控制器设计中, 通过对磁悬浮作动器进行系统建模, 分析控制系统的动态性能, 并通过控制仿真和振动试验研究相结合验证其有效性。
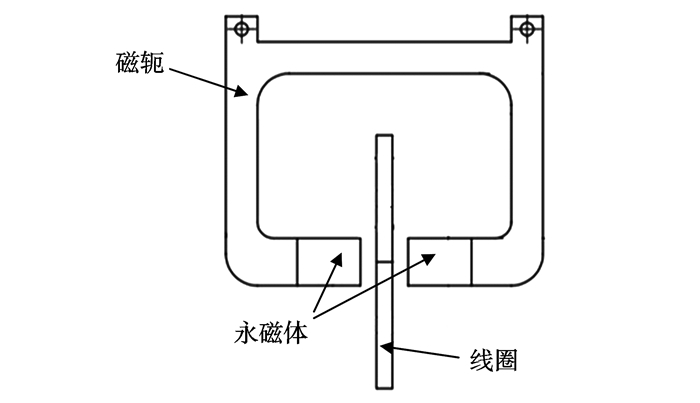
1 磁悬浮作动器串级PID控制建模基于电磁力原理, 磁悬浮作动器可分为两大类。一类是基于麦克斯韦吸引力的作动器, 另一类是基于洛伦兹力的作动器。本研究采用的作动器是自行研制的洛伦兹力作动器, 主要包括线圈组件和磁轭组件, 具体结构如图 1所示。对称分布的永磁体在磁路中提供稳定的磁场, 磁轭下端开口, 使得磁路与线圈的相对位置有更大的调整范围。其原理是由永磁体或电磁铁产生稳定磁场, 该磁场对置于其中的通电导线产生作用力, 其计算公式为F=nBIL, 其中F为线圈在磁场中的受力, 在此可视为作动器作用力; n为线圈匝数, B为导线所处磁场的磁感应强度大小; L则是在磁场中的导线长度。作动器输出力与电流成线性关系。
|
图 1 磁悬浮作动器结构示意图 Figure 1 Structure diagram of magnetic levitation actuator |
理论建模忽略了一些因素导致建立的模型不准确, 为此, 采用系统辨识的方法来建立磁悬浮作动器的数学模型, 具体方法如下:在系统辨识试验中, 给功放提供0.1~200 Hz的1.5 V扫频信号, 利用数据采集仪采集试验对象的时域和频域数据, 然后调用Matlab的系统辨识工具箱, 采用系统辨识方法通过拟合被控对象频域的动态特性, 进而建立磁悬浮作动器的数学模型。考虑到控制复杂程度和模型有效性, 此处采用五阶辨识模型
| $ \begin{array}{l} G\left( s \right) = \\ \frac{{1.7 \times {{10}^3}{s^4} - 2.5 \times {{10}^6}{s^3} + 4.4 \times {{10}^9}{s^2} - 3.2 \times {{10}^{12}}s + 1.5 \times {{10}^{15}}}}{{{s^5} + 1.4 \times {{10}^3}{s^4} + 2.6 \times {{10}^6}{s^3} + 2.1 \times {{10}^9}{s^2} + 1.3 \times {{10}^{12}}s + 3.5 \times {{10}^{14}}}}。\end{array} $ |
单回路PID控制系统在磁悬浮作动器控制方面稳定性不高、控制效果不理想, 为保证隔振系统的性能, 主动隔振采用串级PID控制。串级PID控制由于内环回路的存在, 使得内环回路对象的等效时间常数变小, 缩短了系统的过渡时间, 使控制作用更加及时, 串级PID控制通过减小副回路闭环系统的相位滞后和等效时间常数的方法, 提高了系统的工作效率, 使振荡周期减小, 调节时间缩短, 系统的快速性增强[14-18]。为了从原理上验证串级PID控制的有效性, 考虑到五阶系统的传递函数较为复杂, 本研究以一阶系统为例分析了串级PID控制系统的动态性能。
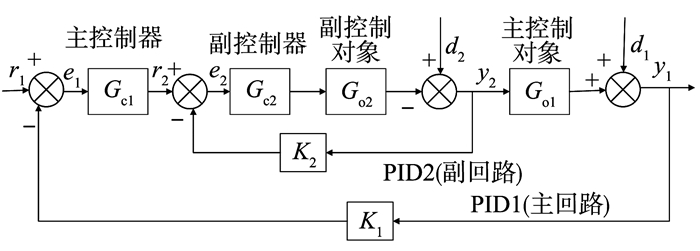
串级PID控制系统结构框图如图 2所示。系统采用两个控制器串联工作, 系统的内环为系统的副回路, 系统的外环为主回路, 外环控制器的输出作为内环控制器的设定值, 由内环控制器的输出去操纵控制阀, 从而对外环被控量具有更好的控制效果。
|
图 2 串级PID控制系统结构图 Figure 2 Structure diagram of cascade PID control system |
图 2中假设:Gc1(s)=Kc1, Gc2(s)=Kc2, Go1(s)=Ko1/(T1s+1), Go2(s)=Ko2/(T2s+1)。其中Kc1、Kc2、Ko1、Ko2 为环节的放大系数或增益, T1、T2为惯性环节的时间常数。单回路控制系统只有Gc1(s)、Go2(s)、Go1(s)和K1,闭环传递函数
| $ \begin{array}{l} \frac{{{c_1}}}{{{r_1}}} = \frac{{{G_{{\rm{c1}}}}{G_{{\rm{o2}}}}{G_{{\rm{o1}}}}}}{{1 + {K_1}{G_{{\rm{c1}}}}{G_{{\rm{o2}}}}{G_{{\rm{o1}}}}}} = \\ \;\;\;\;\;\;\;\frac{{{K_{{\rm{c1}}}}{K_{{\rm{o2}}}}{K_{{\rm{o1}}}}}}{{{s^2} + s \cdot \left( {{T_1} + {T_2}} \right)/T + \left( {{K_{{\rm{c1}}}}{K_{{\rm{o2}}}}{K_{{\rm{o1}}}} + 1} \right)/T}}, \end{array} $ |
式中T=T1T2。
可以得到
| $ 2\xi {\omega _{\rm{n}}} = \left( {{T_1} + {T_2}} \right)/T, $ | (1) |
式中:ωn为无阻尼固有频率; ξ为阻尼比。
系统的有阻尼固有频率
在串级控制系统中, 副回路的开环传递函数
| $ {G_{{\rm{2o}}}}\left( s \right) = {G_{{\rm{c2}}}}\left( s \right){G_{{\rm{o2}}}}\left( s \right); $ |
副回路的闭环传递函数
| $ {G_{{\rm{2c}}}}\left( s \right) = {G_{{\rm{2o}}}}\left( s \right)/\left( {1 + {G_{{\rm{2o}}}}\left( s \right)} \right)。$ |
可知
| $ \angle {G_{{\rm{2c}}}}\left( {j\omega } \right) = \angle {G_{{\rm{2o}}}}\left( {j\omega } \right) - \angle \left[ {1 + {G_{{\rm{2o}}}}\left( {j\omega } \right)} \right], $ |
式中∠G2o(jω)和∠[1+G2o(jω)]表示其相频特性(即相位)。由于∠G2o(jω)和∠[1+G2o(jω)]均为负值, 由式(1)可得∠G2o(jω)<∠[1+G2o(jω)]。副回路闭环系统的相位滞后减小, 系统的稳定性提高。副回路闭环传递函数
| $ \frac{{{c_2}}}{{{r_2}}} = \frac{{{G_{{\rm{c2}}}}{G_{{\rm{o2}}}}}}{{1 + {K_2}{G_{{\rm{c2}}}}{G_{{\rm{o2}}}}}} = \frac{{{K_{{\rm{c2}}}}{K_{{\rm{o2}}}}}}{{{T_2}s + {K_{\rm{2}}}{K_{{\rm{c2}}}}{K_{{\rm{o2}}}} + 1}} = \frac{{{{K'}_2}}}{{{{T'}_2}s + 1}}, $ |
式中:K′2=Kc2Ko2/(K2Kc2Ko2+1)<Ko2; T′2=T2/(K2Kc2Ko2+1)<T2。副回路的等效时间常数减小到T2/(K2Kc2Ko2+1), 相当于在系统中增加了一个微分环节, 使得系统的反应速度加快, 控制更为及时。等效对象放大倍数的减小可以通过增加主动控制器的增益加以补偿。整个系统的闭环传递函数
| $ \begin{array}{l} \frac{{{c_1}}}{{{r_1}}} = \\ \frac{{{K_{{\rm{c1}}}}{K_{{\rm{c2}}}}{K_{{\rm{o2}}}}{K_{{\rm{o1}}}}/T}}{{{s^2} + s \cdot \left( {{T_1} + {T_2} + {T_1}{K_2}{K_{{\rm{c2}}}}{K_{{\rm{o2}}}}} \right)/T + \left( {{K_2}{K_{{\rm{c2}}}}{K_{{\rm{o2}}}} + {K_{{\rm{c1}}}}{K_{{\rm{c2}}}}{K_{{\rm{o2}}}}{K_{{\rm{o1}}}} + 1} \right)/T}}, \end{array} $ |
式中T=T1T2。
同式(1)可得
| $ 2\xi '{{\omega '}_{\rm{n}}} = {T_1} + {T_2} + {T_1}{K_2}{K_{{\rm{c2}}}}{K_{{\rm{o2}}}}/\left( {{T_1}{T_2}} \right), $ | (2) |
式中:ω′n为无阻尼固有频率; ξ′为阻尼比。
系统的有阻尼固有频率
假设两种情况下阻尼比相同, 由式(1)和(2)可得
| $ \frac{{{{\omega '}_{\rm{d}}}}}{{{\omega _{\rm{d}}}}} = \frac{{{T_1} + {T_2} + {T_1}{K_2}{K_{{\rm{c2}}}}{K_{{\rm{o2}}}}}}{{{T_1} + {T_2}}} = 1 + \frac{{{K_2}{K_{{\rm{c2}}}}{K_{{\rm{o2}}}}}}{{1 + {T_2}/{T_1}}}。$ |
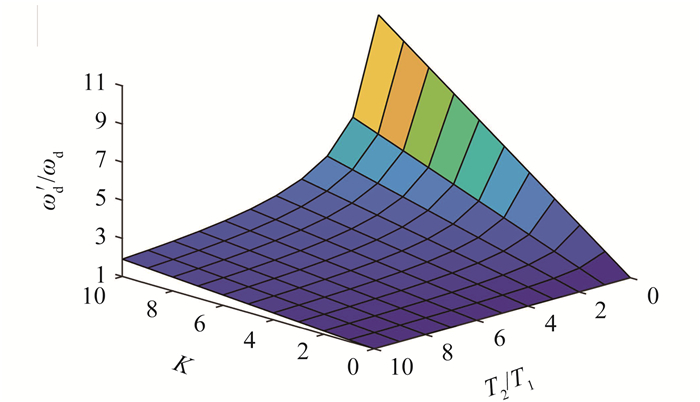
令K=K2Kc2Ko2, 则ω′d/ωd与K和T2/T1的关系曲线如图 3所示。从图 3中可得副控制器的增益Kc2越大(即K越大), 或者随着T2/T1的减小, 串级控制系统有阻尼频率提高的越明显。在相同阻尼比的条件下, 串级控制系统的有阻尼频率高于单回路系统, 系统的有阻尼频率提高, 根据公式
| $ {t_s} = - \ln \Delta /\left( {\xi {\omega _n}} \right), $ | (3) |
|
图 3 K和T2/T1对ω′d/ωd的影响 Figure 3 The effect of Kand T2/T1 on ω′d/ωd |
得到系统调整时间ts缩短使得控制质量得到改善。式(3)中Δ为指定的微小量, 一般取Δ=0.02~0.05。
在磁悬浮作动器串级PID控制中, 加速度环为系统的副回路, 位置环为主回路。当被隔振物体产生加速度扰动时, 加速度控制器根据偏差信号产生控制力抵消惯性运动。由于隔振台的加速度使隔振台产生漂移, 主控制器(位移控制器)通过外回路及时调节副控制器(加速度控制器)的设定, 使加速度初值变化, 而副控制器一方面接受主控制器的输出信号, 同时根据加速度计测量值进行调节, 使载荷加速度跟踪设定值变化, 根据隔振台位移及时调整, 最终使其位移回复到中心位置。
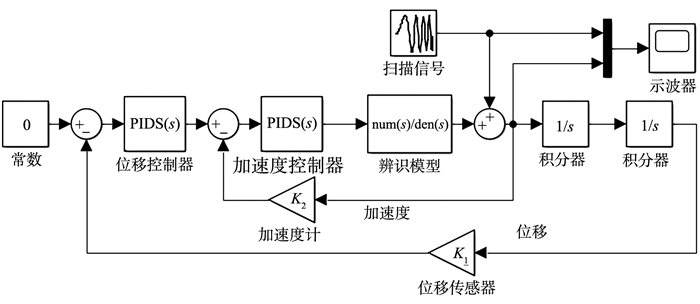
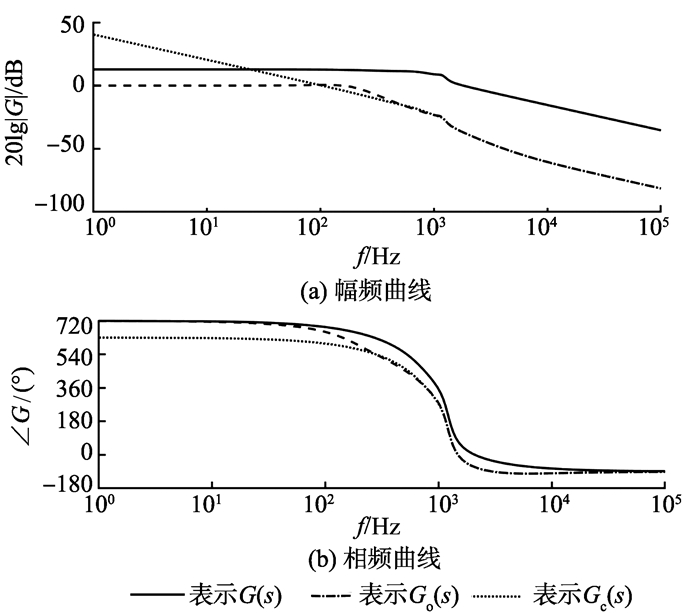
2 基于Matlab的作动器串级PID控制仿真在Matlab中建立如图 4所示的仿真试验框图, 利用Simulink的自整定功能首先整定副回路控制器PID参数, 再确定主回路控制器PID参数。系统副回路的辨识传递函数G(s)、开环传递函数Go(s)和闭环传递函数Gc(s)的Bode图如图 5所示。从图 5中可以看到, 辨识传递函数加入PID控制器后闭环系统的幅值裕度和相位滞后明显减小了, 幅值裕度的减小可以适当增加主控制器增益。
|
图 4 串级PID仿真控制框图 Figure 4 Cascade PID simulation control block diagram |
|
图 5 G(s)、Go(s)和Gc(s)的Bode图 Figure 5 Bode diagrams of G(s), Go(s) and Gc(s) |
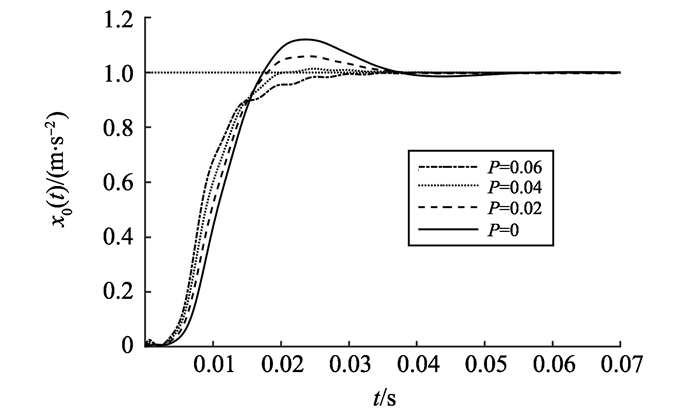
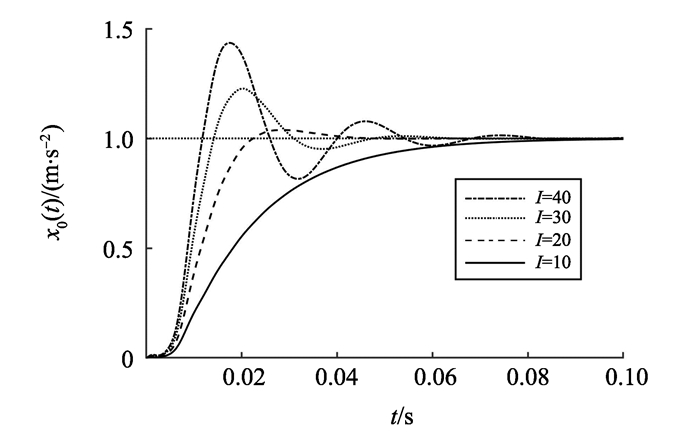
控制器比例P和积分I变化的系统阶跃响应分别如图 6和7所示。仿真结果与前文分析的串级PID控制系统的性能分析结论一致:在相同阻尼比下副回路PID控制器增益越大, 超调变大, 系统的有阻尼频率提高, 系统阶跃响应的调整时间ts缩短, 控制质量得到改善; I越大, 系统的超调变大, 调整时间ts缩短, 但系统的振荡次数会增加。
|
图 6 P变化的副回路系统的阶跃响应 Figure 6 Step response of the sub loop system of P change |
|
图 7 I变化的副回路系统的阶跃响应 Figure 7 Step response of the sub loop system of I change |
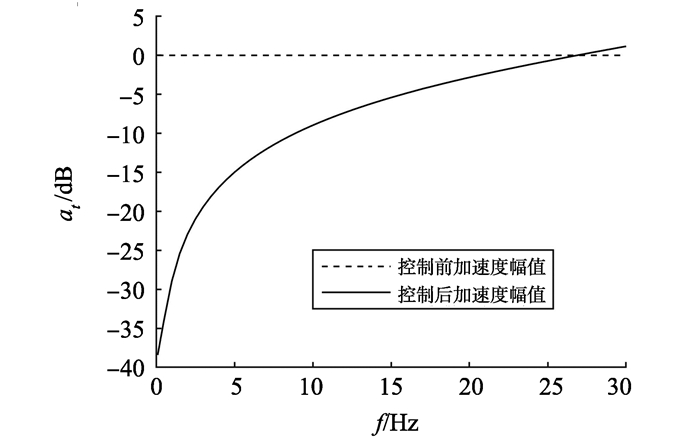
对系统施加频率0.1~30 Hz幅值为1的加速度扫频信号, 得到如图 8所示的主动控制下加速度传递率。从图 8中可以得出, 在主动控制作用下, 加速度传递率的衰减幅度为-38.4~2.9 dB。在0.1~10 Hz的频率范围内, 系统有较好的隔振性能, 加速度传递率降低约-40~-10 dB。随着加速度频率的提高, 系统在10~20 Hz的频率范围内加速度传递率降低约-10~-3 dB。通过以上数据可以得出仿真试验所设计的串级PID控制器对0.1~10 Hz频段的加速度扰动信号具有较好地控制效果。
|
图 8 主动控制下加速度传递率 Figure 8 Acceleration transfer rate under active control |
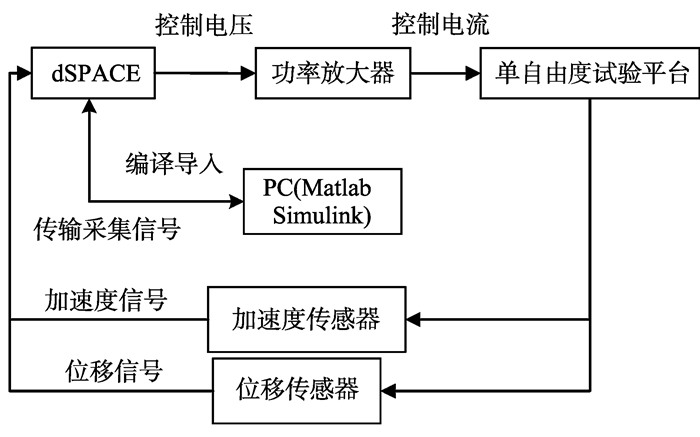
为验证串级PID应用在磁悬浮作动器低频振动主动控制的实际应用效果, 设计了单自由度主动控制试验系统。控制系统框图如图 9所示。系统由计算机(personal computer, PC)、dSPACE和单自由度主动控制试验平台组成。系统将Simulink建立的控制仿真模型编译成代码后导入到dSPACE中, 然后通过dSPACE的A/D模块采集传感器的电压信号, 基于采集的数据完成控制算法的计算并将控制电压传送给功率放大器, 功率放大器输出控制电流, 从而实现作动器的位置和加速度控制。
|
图 9 基于dSPACE的实时控制系统框图 Figure 9 Block diagram of time control system based on dSPACE |
控制系统试验设备和单自由度振动控制试验装置如图 10和11所示。该装置主要包括磁悬浮作动器、直线滚动单元(本研究中用小车代替)、加速度传感器、激光源、位移传感器、振动电机、功率放大器、恒流电压源和dSPACE实时仿真系统。

|
图 10 控制系统试验设备 Figure 10 Control system experimental equipment |

|
图 11 单自由度振动控制试验装置 Figure 11 Experimental device for vibration control of singledegree of freedom |
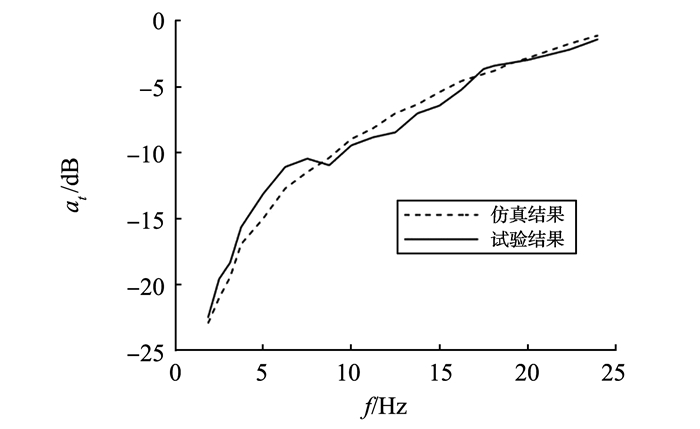
试验时, 通过调节振动电机输入电压改变振动电机产生扰动加速度的频率和幅值, 数据采集仪采集加速度信号, 并利用其自带的分析软件获得主动控制前后的振动加速度信号。将试验测得主动控制下的1~25 Hz频段和仿真试验对比的结果如图 12所示。在1~20 Hz频率范围内, 试验测得的加速度传递率随频率的变化范围趋势和仿真结果一致。不同频率处的加速度传递率和仿真数据基本相同。
|
图 12 试验和仿真的加速度传递率结果对比 Figure 12 Comparison of experimental and simulated results ofacceleration transfer rate |
各频率的振动加速度衰减数据见表 1。表中f代表频率, a1代表控制前加速度, a2代表控制后加速度, Δa表示加速度衰减。在1~25 Hz频段, 应用串级PID控制方法对振动电机产生的振动进行了有效衰减, 加速度衰减幅度最高为-22.5 dB, 随着频率增加, 衰减幅度减小。在1~25 Hz频段衰减幅度为-22.5~-2.2 dB, 和仿真试验的结果基本一致。
| 表 1 振动加速度衰减结果 Table 1 Vibration acceleration attenuation result |
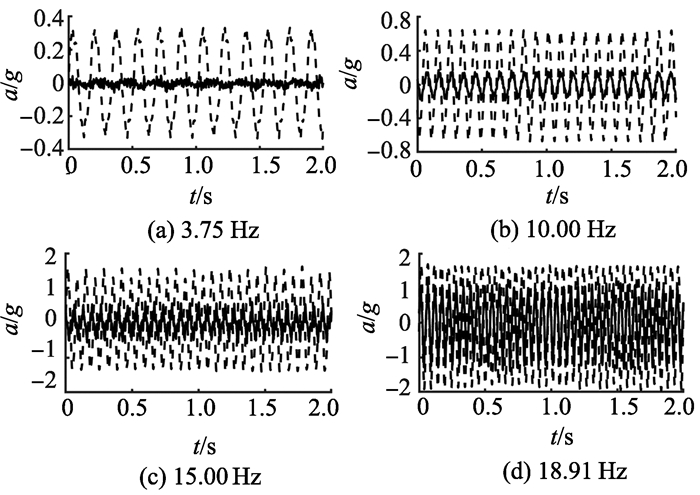
由于篇幅限制, 选取四组频率差值约为5 Hz的控制前后的加速度时域数据, 如图 13所示。当频率为3.75、10.00、15.00和18.91 Hz时, 在控制后振动加速度明显衰减。振动电机的单频振动频率为1~25 Hz时, 采用串级PID控制方法对磁悬浮作动器的加速度水平进行衰减, 衰减幅度为-22.5~-2.2 dB。结果表明:应用串级PID控制方法实现了有效的振动控制。
|
图 13 试验的加速度控制效果 Figure 13 The effect of acceleration control in the experiment 注:虚线、实线分别表示控制前和控制后加速度; g为重力加速度 |
本研究提出了一种基于洛伦兹力原理的磁悬浮作动器的串级PID控制研究方法, 该方法通过减小副回路闭环系统的相位滞后和等效时间常数, 提高了系统稳定性和响应速度, 通过副回路控制器增益增加串级控制系统有阻尼频率, 缩短系统的调节时间, 提高系统控制质量。通过仿真和试验研究, 采用串级PID控制方法, 当控制对象的频率范围为1~25 Hz时, 衰减幅度为-22.5~-2.2 dB, 实现了有效的振动控制。
在主动隔振控制方面, 串级PID控制方法设计简单、结构灵活、鲁棒性较强, 但依赖对象模型确定, 当对象模型和参数不确定时, 控制效果不明显。在实际工程中, 即使确定数学模型, 环境、材料等改变也会给物理参数带来影响, 进而导致设备传递函数发生变化, 加之各种扰动的作用, 控制特性变化很大。而近年来随着神经网络的发展, 给PID控制器的设计提供了新思路, 神经网络具有逼近任意的非线性函数的表达能力, 能够有效处理常规PID控制器在控制中的三个参数的调整问题, 即利用神经网络的自学习、自适应能力来改善串级PID控制, 来进一步优化主动隔振系统的性能。
| [1] | WU Qianqian, YUE Honghao, LIU Rongqiang, et al. Parametric design and multiobjective optimization of maglev actuators for active vibration isolation system[J]. Advances in Mechanical Engineering, 2015, 6(8): 215358-215358 |
| [2] | LI Weipeng, HUANG Hai, ZHOU Xubin, et al. Design and experiments of an active isolator for satellite micro-vibration[J]. Chinese Journal of Aeronautics, 2014, 27(6): 1461-1468 DOI:10.1016/j.cja.2014.10.012 |
| [3] | EDBERG D, BOUCHER R, NURRE G, et al. Performance assessment of the STABLE microgravity vibration isolation flight demonstration[C]//Structures, Structural Dynamics, and Materials Conference. Boston, America: AIAA, 1997: 7-10. http://www.researchgate.net/publication/268463833_Performance_assessment_of_the_STABLE_Microgravity_Vibration_Isolation_Flight_Demonstration |
| [4] | WOODARD S, HOUSNER J. Nonlinear behavior of a passive zero spring-rate suspension system[J]. Journal of Guidance Control and Dynamics, 1991, 14(1): 84-89 DOI:10.2514/3.20608 |
| [5] | 王佳. 高微重力平台主动振动隔离系统控制器设计与仿真试验[D]. 北京: 中国科学院研究生院, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2055045 |
| [6] |
李宗峰, 任维佳. 空间微重力主动隔振技术研究[J].
载人航天, 2010, 16(3): 24-32 LI Zongfeng, REN Weijia. Study on the space microgravity active vibration isolation techniques[J]. Manned Spaceflight, 2010, 16(3): 24-32 DOI:10.3969/j.issn.1674-5825.2010.03.005 |
| [7] | YANG Bongjun, CALISE A, CRAIG J, et al. Adaptive control for a microgravity vibration isolation system[C]//Navigation, and Control Conference and Exhitbt. San Francisco, USA: AIAA Guidance, 2005: 1-19. http://www.researchgate.net/publication/24372046_Adaptive_Control_for_Microgravity_Vibration_Isolation_System |
| [8] |
赵伟. 航天器微振动环境分析与测量技术发展[J].
航天器环境工程, 2006, 23(4): 210-214 ZHAO Wei. Analysis on micro-vibration environment of spacecraft and measurement technology[J]. Spacecraft Environment Engineering, 2006, 23(4): 210-214 DOI:10.3969/j.issn.1673-1379.2006.04.005 |
| [9] | CARRELLA A, BRENNAN M, WATERS T. Static analysis of a quasi-zero-stiffness vibration isolator[J]. Journal of Sound and Vibration, 2007, 301: 678-689 DOI:10.1016/j.jsv.2006.10.011 |
| [10] |
安峰岩, 孙红灵, 肖椽生, 等. 基于磁悬浮作动器的自适应有源振动控制研究[J].
声学学报, 2010, 35(2): 146-153 AN Fengyan, SUN Hongling, XIAO Chuansheng, et al. Research on adaptive active vibration control using maglev actuator[J]. Journal of Acoustics, 2010, 35(2): 146-153 |
| [11] | HU Yefa, CHEN Changhao, WU Huachun, et al. Study on structural optimization design and cascade PID control of maglev actuator for active vibration isolation system[J]. Journal of Vibration & Control, 2017, 24(10): 1829-1847 |
| [12] | KIM Y, WHORTON M. Equations of motion for the g-LIMIT microgravity vibration isolation system[R]. Alabama, USA: Marshall Space Flight Center, 2001. https://www.researchgate.net/publication/24296806_Equations_of_Motion_for_the_g-LIMIT_Microgravity_Vibration_Isolation_System |
| [13] | 段小帅. 磁悬浮隔振器的动态建模与自收敛控制[D]. 合肥: 中国科学技术大学, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D075400 |
| [14] |
宋春生. 柔性浮筏系统的磁悬浮主动隔振理论与控制技术研究[D]. 武汉: 武汉理工大学, 2011.
SONG Chunsheng. Study on theory and control technology of magnetic suspension active vibration isolation for flexible floating raft system[D]. Wuhan: Wuhan University of Technology, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1948884 |
| [15] | HE Wei, DAVID A, YIN Zhao, et al. Neural network control of a robotic manipulator with input deadzone and output constraint[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2016, 46(6): 759-770 |
| [16] | WHORTON M. Robust control for microgravity vibration isolation with parametric uncertainty[C]//American Control Conference: vol. 1. Montréal, Canada: IEEE, 2002: 256-261. https://ieeexplore.ieee.org/document/1024813/ |
| [17] |
文增红. 基于BP神经网络PID的控制系统研究[J].
电脑知识与技术, 2013(28): 6375-6377 WEN Zenghong. The control system researching based on BP neural network PID[J]. Computer Knowledge and Technology, 2013(28): 6375-6377 |
| [18] |
陈波. 基于神经网络PID控制的两轮自平衡小车研究[D]. 成都: 西南交通大学, 2014.
CHEN Bo. The research of two-wheeled self-balanced vehicle based on PID neural network[D]. Chengdu: Southwest Jiao Tong University, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2577849 |



