2. 西安交通大学机械结构强度与振动国家重点试验室, 陕西 西安 710049
2. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi′an Jiaotong University, Xi′an 710049, Shaanxi, China
随着科技的发展, 越来越多的人力劳动被机械替代, 机械自动化程度越来越高, 在工业生产线上, 人们设计出多种多样的机械臂以满足不同的工业需求。然而这类结构包含的时变参数和弹性振动的复杂耦合特性导致柔性机械臂易产生大幅值、慢衰减的变频振动或者多频振动, 严重影响系统定位精度和运动稳定性。
含变质量参数、变阻尼参数、变刚度参数的结构动力响应问题很早就引起了国内外研究者的注意[1-2], 尤其是变质量系统的动力学建模问题, 研究人员发展了多种有效的研究方法。陈占清等[3-4]在变质量刚性质点系动力学理论基础上, 考虑结构变形, 建立了变质量挠性体的动力学一般方程, 然后以固体燃料运载火箭这类变质量系统为对象, 采用连续介质力学中的平衡理论和分析力学中的变分原理建立了这类挠性体的动力学方程。张耀良等[5]研究了变质量非完整、非保守系统中守恒量存在的必要条件, 建立了系统的Hamilton正则方程的守恒定理, 该建模方法具有广泛的应用价值。朱岩等[6]采用改进的多尺度方法对变质量振动系统进行近似求解, 通过数值仿真发现幅值变化系数的不同只影响系统振幅, 而不改变系统振动响应的周期。M. Kaliyoncu[7]分析了含变质量的关节机械臂结构的运动规律, 研究了关节运动和质量变化对系统的影响。S. Nhleko[8]对变质量时变系统的参数取值范围进行了细致的划分, 研究了变质量系统自由振动的响应规律, 讨论了时变质量引起的附加阻尼特性, 并给出了振动稳定的临界阻尼条件。随着车辆的普及, 人们对交通工具的舒适度要求越来越越高, 在座椅结构设计中必须考虑不同的坐姿与质量对结构的影响, I. Maciejewski等[9]分析了质量变化载荷下, 主动悬架式座椅的微振动抑制问题。L. Cveticanin[10-11]对带有变质量的振子系统和转子系统进行了一系列研究, 开展了变质量振子和变质量转子的模态分析、稳定性分析以及非线性动力学分析。J. A. Richards[12]和W. T. Van Horssen等[13-15]则重点分析了质量周期变化的有阻尼单自由度系统的稳定性。以上研究中关于变质量系统动力学问题, 对象以单自由度系统或者少自由度系统为主, 而随着工业化程度的提高, 结构更加复杂化、精细化、模块化, 因此有必要开展复杂连续变质量结构的动力学分析。对于多自由度系统, 往往难以得到解析解, 随着计算机的发展, 数值方法拥有了更广阔的使用空间。王宇楠等[16]提出了适用于变质量系统的自适应Newmark法, 分析了质量变化对系统动特性的影响。ZHAO Rui等[17]基于Meshchersky基本方程, 推导了变质量系统的Hamilton′s定律, 并建立了新型有限元公式, 对于质量变化系统和移动质量系统, 计算精度高, 收敛快。F.Mazenc等[18]针对含时滞的线性时变系统的稳定性问题, 提出了缩减模型方法, 该方法对慢变系统和快变系统都有良好的适应性。杜妍辰等[19]对变质量碰撞振动系统进行求解分析, 采用渐近法对变质量振动方程进行近似解析求解, 发现变质量会使系统响应产生一定的突变。于开平[20]针对以大型运载火箭为代表的变质量航天器结构, 提出了变质量系统的变作用哈密顿原理, 用变质量系统哈密顿原理建立了线性变质量柔性结构的有限元动力学方程, 该方法算法稳定, 具有普遍的适用性。
在变质量结构或者变刚度结构振动测试试验中, 很难设计具有稳定可控时变参数的试件, 并且在振动信号中既含变频信号, 也有多频信号, 测量难度大, 可操作性低。相对于数值分析, 试验研究发展较慢。J. Flores[21]以单自由度振子为试验对象开展了变质量时变系统的初步研究。舒俊成[22]采用光滑不连续振子建立变质量模型, 从试验和理论仿真两个角度分析了该类结构非线性动力学行为。T.Bartkowiak等[23]通过变质量单摆结构的数值分析和试验研究, 分析了质量变化对系统的影响。虽然目前开展了一些变质量系统相关的振动测试试验, 但这些试验多以单自由度系统为试验对象, 而随着工业自动化技术要求的提高, 迫切需要开展变质量弹性结构的振动测试。为进一步研究变质量作用下板梁弹性结构的振动特性, 本研究从理论上建立变质量-柔性结构的动力学模型, 分析该类变质量系统的动力学特性, 并设计相关的动力学测试试验, 通过控制水的流入流出实现系统质量的稳定变化, 根据数值仿真和试验测试总结了变质量系统的运动规律。
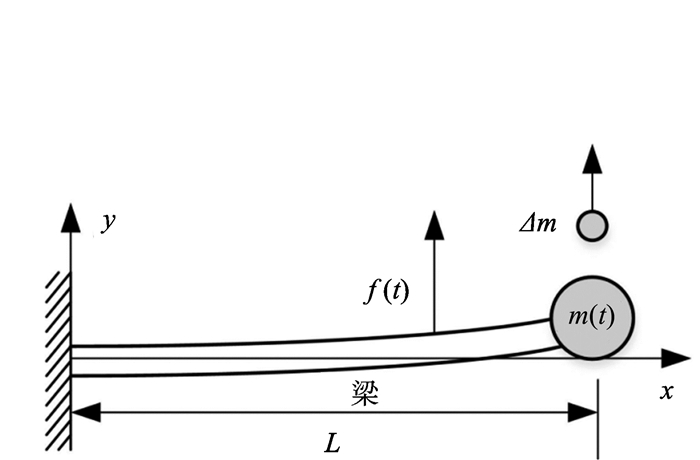
1 数学模型图 1所示为含变质量构件的柔性悬臂梁结构, 其中梁的长度为L, 受到外力f(t)的作用。梁末端附带一个集中质量, 该质量是时间的函数, 定义为m(t), Δm表示在t到t+Δt这段时间内流入或者流出的质量。对于柔性欧拉梁结构, 在研究中只考虑梁结构的弯曲振动w(x, t)即可满足计算要求。
|
图 1 附加变质量构件的梁结构 Figure 1 A flexible beam with a time varying mass |
对于图 1所示的含变质量构件的悬臂梁结构, 系统的势能T为梁结构的变形能, 计算式为
| $ T = \frac{1}{2}\int_0^L {EI\left( {\frac{{{\partial ^2}w}}{{\partial {x^2}}}} \right){\rm{d}}x} , $ | (1) |
式中:E为材料的弹性模量; I为梁横截面惯性矩。梁结构和末端质量的动能之和为系统的动能
| $ V = \frac{1}{2}\int_0^L {\rho A{{\left( {\frac{{\partial w}}{{\partial t}}} \right)}^2}{\rm{d}}x} + \frac{1}{2}m\left( t \right)\delta \left( {x - L} \right){\left( {\frac{{\partial w}}{{\partial t}}} \right)^2}, $ | (2) |
式中:ρ为梁的密度; A为梁的横截面积; δ(x-L)为集中质量的位置。对式(1)分部积分, 结合式(2), 令L=V-T, 根据Lagrange方程
| $ \frac{{\partial L}}{{\partial w}} - \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial \dot w}}} \right) = f, $ |
推导出含变质量构件的梁结构的运动方程
| $ EI\frac{{{\partial ^4}w}}{{\partial {x^4}}} + \rho A\ddot w + \delta \left( {x - L} \right)\frac{{{\rm{d}}\left( {m\dot w} \right)}}{{{\rm{d}}t}}。$ | (4) |
当系统末端质量不变时, d(m
| $ EI\frac{{{\partial ^4}w}}{{\partial {x^4}}} + \dot m\delta \left( {x - L} \right)\dot w + \left( {\rho A + m\delta \left( {x - L} \right)} \right)\ddot w = f\left( t \right)。$ | (4) |
在以往的研究中, 特别是工程分析中, 人们往往忽略附加阻尼的作用, 如果忽略质量变化引起的阻尼, 系统的运动方程变为
| $ EI\frac{{{\partial ^4}w}}{{\partial {x^4}}} + \left( {\rho A + m\delta \left( {x - L} \right)} \right)\ddot w = f\left( t \right)。$ | (5) |
对于图 1所示悬臂梁结构, 需要满足以下边界条件:
| $ w\left( t \right)\left| {_{x = 0}} \right. = 0, $ |
| $ \frac{{\partial w\left( t \right)}}{{\partial x}}\left| {_{x = 0}} \right. = 0, $ |
| $ \frac{{{\partial ^2}w\left( t \right)}}{{\partial {x^2}}}\left| {_{x = L}} \right. = 0, $ |
| $ EI\frac{{{\partial ^3}w\left( t \right)}}{{\partial {x^3}}} + \frac{{{\rm{d}}m\left( t \right)\dot w\left( t \right)}}{{{\rm{d}}t}}\left| {_{x = L}} \right. = 0。$ |
基于模态叠加方法, 方程(4)(5)的解可以表示为多阶模态函数组合的形式:
| $ w\left( {x,t} \right) = \sum\limits_{i = 1}^n {{\varphi _i}\left( {x,t} \right){\eta _i}\left( t \right)} = {\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\mathit{\boldsymbol{\eta }}, $ | (6) |
式中: φ=[φ1 φ2 … φn]T为模态函数; η=[η1 η2 … ηn]T为广义坐标。由于系统末端质量随时间变化, 因此振型函数应为空间和时间的函数:
| $ {\varphi _i}\left( {x,t} \right) = {C_i}\left( t \right)\left[ {\sin {\beta _i}x - \sinh {\beta _i}x + {r_i}\left( {\cos {\beta _i}x - \cosh {\beta _i}x} \right)} \right], $ | (7) |
式中:Ci(t)为振型函数系数; βi为特征频率; 参数ri=
| $ \begin{array}{*{20}{c}} {\int_0^L {\delta {\mathit{\boldsymbol{\eta }}^{\rm{T}}}\mathit{\boldsymbol{\varphi }} \cdot EI\frac{{{\partial ^4}{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\mathit{\boldsymbol{\eta }}}}{{\partial {x^4}}}{\rm{d}}x} + \delta {\mathit{\boldsymbol{\eta }}^{\rm{T}}}\mathit{\boldsymbol{\varphi }} \cdot \dot m\frac{{{\rm{d}}{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\mathit{\boldsymbol{\eta }}}}{{{\rm{d}}t}}\left| {_{x = L}} \right. +\\ \int_0^L {\delta {\mathit{\boldsymbol{\eta }}^{\rm{T}}}\mathit{\boldsymbol{\varphi }} \cdot \rho A\frac{{{{\rm{d}}^2}{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\mathit{\boldsymbol{\eta }}}}{{{\rm{d}}{t^2}}}{\rm{d}}x} + \delta {\mathit{\boldsymbol{\eta }}^{\rm{T}}}\mathit{\boldsymbol{\varphi }} \cdot m\frac{{{{\rm{d}}^2}{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\mathit{\boldsymbol{\eta }}}}{{{\rm{d}}{t^2}}}\left| {_{x = L}} \right. = }\\ {\delta {\mathit{\boldsymbol{\eta }}^{\rm{T}}}\mathit{\boldsymbol{\varphi }} \cdot f\left( t \right)\left| {_x} \right.,} \end{array} $ | (8) |
最终得到系统的运动方程
| $ \mathit{\boldsymbol{M\ddot \eta }} + \mathit{\boldsymbol{C\dot \eta }} + \mathit{\boldsymbol{K\eta }} = \mathit{\boldsymbol{F}}, $ | (9) |
式中:M、C、K和F分别为系统的质量矩阵、阻尼矩阵、刚度矩阵和载荷向量, 矩阵和向量中元素的具体表达式为:
| $ {M_{ij}} = \int_0^L {\rho A{\varphi _i}{\varphi _j}{\rm{d}}x} + m\left( t \right){\varphi _i}{\varphi _j}\left| {_{x = L}} \right., $ | (10) |
| $ {C_{ij}} = \int_0^L {2\rho A{{\dot \varphi }_i}{\varphi _j}{\rm{d}}x} + 2m\left( t \right){{\dot \varphi }_i}{\varphi _j}\left| {_{x = L}} \right. + \dot m\left( t \right){\varphi _i}{\varphi _j}\left| {_{x = L}} \right., $ | (11) |
| $ {K_{ij}} = \int_0^L {EI{{\varphi ''}_i}{{\varphi ''}_j}{\rm{d}}x} + \int_0^L {\rho A{{\ddot \varphi }_i}{\varphi _j}{\rm{d}}x} + \dot m\left( t \right){{\dot \varphi }_i}{\varphi _j}\left| {_{x = L}} \right. + m\left( t \right){{\ddot \varphi }_i}{\varphi _j}\left| {_{x = L}} \right., $ | (12) |
| $ {F_i} = {\varphi _i}f\left( t \right)\left| {_x} \right.。$ | (13) |
由式(10)~(13)可知, 由于振型函数φ(t)和质量函数m(t)具有时变性, 除了直接改变系统的总质量, 还会产生附加刚度(Kij中第二、三、四项)和附加阻尼(Cij)。对于弹性结构还应考虑结构阻尼, 本研究用比例阻尼近似, 前二阶模态阻尼比α和β分别取0.1%和0.025%。因此系统的完整动力学方程为
| $ \mathit{\boldsymbol{M\ddot \eta }} + \left( {\mathit{\boldsymbol{C}} + \alpha \mathit{\boldsymbol{M}} + \beta \mathit{\boldsymbol{K}}} \right)\mathit{\boldsymbol{\dot \eta }} + \mathit{\boldsymbol{K\eta }} = \mathit{\boldsymbol{F}}。$ | (14) |
为了研究质量变化引起的附加项
| $ \mathit{\boldsymbol{M\ddot \eta }} + \left( {\mathit{\boldsymbol{C'}} + \alpha \mathit{\boldsymbol{M}} + \beta \mathit{\boldsymbol{K'}}} \right)\mathit{\boldsymbol{\dot \eta }} + \mathit{\boldsymbol{K'\eta }} = \mathit{\boldsymbol{F}}, $ | (15) |
式中:C′和K′分别表示忽略质量变化引起的附加项
对于时变系统, 系统的质量、刚度和阻尼都可能是时变的, 因此在迭代计算中每一个步长都需要更新参数矩阵, 导致计算量剧增, 算法的改进是提高计算效率的一种有效措施。在动力学计算中, Newmark法以其稳定性和高效率应用非常普遍, 如著名的商业有限元软件Ansys, 在瞬态响应分析中便是采用Newmark法计算系统的动态响应, Newmark方法中积分参数的选择直接决定了计算精度和计算效率。
经典Newmark法的迭代计算公式为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}}\left( {k + 1} \right) = \mathit{\boldsymbol{\dot x}}\left( k \right) + h\left[ {\left( {1 - \gamma } \right)\mathit{\boldsymbol{\ddot x}}\left( k \right) + \gamma \mathit{\boldsymbol{\ddot x}}\left( {k + 1} \right)} \right]\\ \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{x}}\left( k \right) + h\mathit{\boldsymbol{x}}\left( k \right) + \frac{{{h^2}}}{2}\left[ {\left( {1 - 2\theta } \right)\mathit{\boldsymbol{\ddot x}}\left( k \right) + 2\theta \mathit{\boldsymbol{\ddot x}}\left( {k + 1} \right)} \right] \end{array} \right., $ |
式中: x(k+1)、
| $ h\left( t \right) = \frac{{2{\rm{ \mathsf{ π} }}}}{{\kappa {\omega _1}\left( t \right)}}, $ | (16) |
| $ \theta \left( t \right) = \frac{1}{{\mathit{\Gamma }\left( t \right)}} - \frac{1}{{\omega _1^2\left( t \right){h^2}\left( t \right)}} - \frac{{{\xi _1}}}{{{\omega _1}\left( t \right)h\left( t \right)}}, $ |
式中:κ为步长控制因子; ω1(t)为模态叠加法中采用的第一阶模态的振动角频率; ξ1为系统的第一阶模态阻尼比; h(t)为自适应步长。参数Γ(t)和Ω(t)根据系统第一阶振动的相位零误差条件[16]得到:
| $ \mathit{\Gamma }\left( t \right) = \frac{2}{{{\mathit{\Omega }^2}}}\left[ {\frac{{1 + \mathit{\Omega }{{\tan }^2}{\omega _1}h - \sqrt {1 + 2\mathit{\Omega }{{\tan }^2}{\omega _1}h - {\mathit{\Omega }^2}{{\tan }^2}{\omega _1}h} }}{{1 + {{\tan }^2}{\omega _1}h}}} \right], $ |
| $ \mathit{\Omega }\left( t \right) = 1 + \frac{{2{\xi _1}\left( t \right)}}{{{\omega _1}\left( t \right)h\left( t \right)}}。$ |
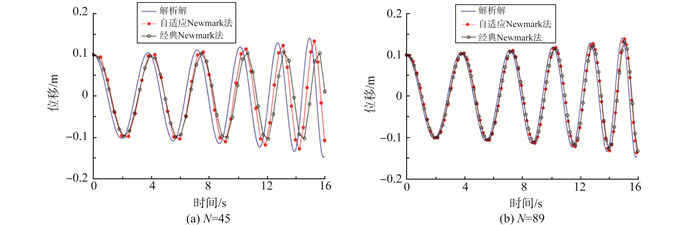
以文献[7]中的变质量系统为例, 采用自适应Newmark和经典Newmark法分别计算了的系统位移响应, 如图 2所示。根据式(16), κ决定了计算步长, 也就是决定了迭代次数N。当κ=4时, N=45;κ=8时, N=89。对比响应曲线可知, 自适应Newmark法得到的结果更接近精确值, 计算效率更高, 更适合时变参数系统的动力学响应求解。
|
图 2 变质量系统的位移响应 Figure 2 Displacement of a time varying mass system |
仿真计算中采用的梁结构几何参数与材料参数如表 1所示。末端时变质量按线性规律变化:
| $ m\left( t \right) = {m_0} + {R_{\rm{m}}}t, $ |
| 表 1 梁结构的参数 Table 1 Parameters of beam structure |
式中:Rm为质量变化率; m0为初始质量质量, 质量减少时m0=2.15 kg, 其中变质量构件为0.85 kg, 水的质量为1.3 kg; 质量增加时, m0=0.85 kg。
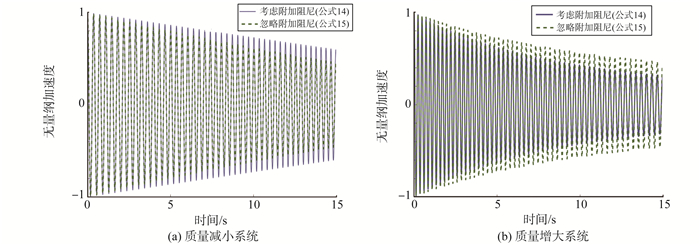
针对式(14)(15), 使用自适应Newmark法计算悬臂梁末端的加速度响应。仿真中质量减少系统和质量增大系统的质量变化率分别取-0.05 kg/s和0.05 kg/s, 响应曲线如图 3所示。由图 3可以看出, 非结构附加阻尼对系统振动有显著影响。当质量减少时, 系统的响应衰减减慢, 这是质量变化产生的负阻尼效应引起的; 当系统质量增大时, 系统的振动衰减加速, 这是质量变化产生的正阻尼效应引起的。因此在质量时变系统振动分析中, 必须考虑质量变化的附加阻尼效应, 尤其是质量减少系统。同时在计算中发现, 系统的振型变化较小, 因此振型函数对时间的一阶导数与二阶导数都比较小, 但是质量对时间的导数较大, 产生的附加作用更显著。
|
图 3 变质量时系统的响应曲线 Figure 3 Dynamic responses of time varying mass system |
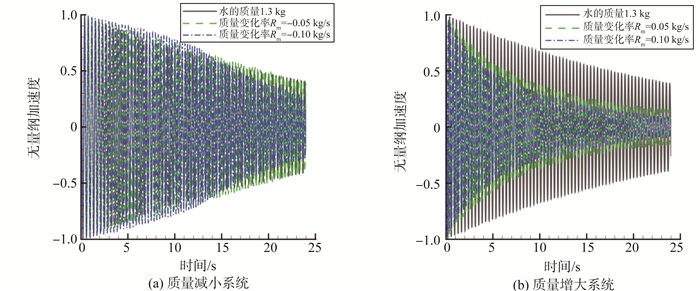
为定量分析附加阻尼的影响, 模拟了不同质量变化率时系统的响应, 使用自适应Newmark法计算得到的加速度曲线如图 4所示。从图 4(a)中可以看出, 末端质量减小越快, 系统的衰减越慢; 在0~13 s, Rm=-0.1 kg/s工况下系统的响应幅值明显大于Rm=-0.05 kg/s时, 原因是dm(t)/dt越大, 引起的非结构负阻尼越大。而水的初始质量为1.3 kg, 当Rm=-0.1 kg/s时, 有效的质量变化时间为0~13 s, 13 s后, 质量不再变化, 附加负阻尼消失, 阻尼变为无水时系统的阻尼, 因此衰减加速; 而Rm=-0.05 kg/s时, 负阻尼一直存在, 导致响应幅值超过Rm=-0.1 kg/s工况下。反之, 当末端质量增大时, 质量增加越快, 系统振动的衰减越快, 如图 4(b)所示。综上所示, 系统质量变化引起的附加阻尼效应对系统的影响非常显著, 尤其是分析质量减少系统的动力学响应时, 必须考虑质量减少引起的附加负阻尼的影响。
|
图 4 变质量时系统的响应曲线 Figure 4 Dynamic responses of time varying mass system |
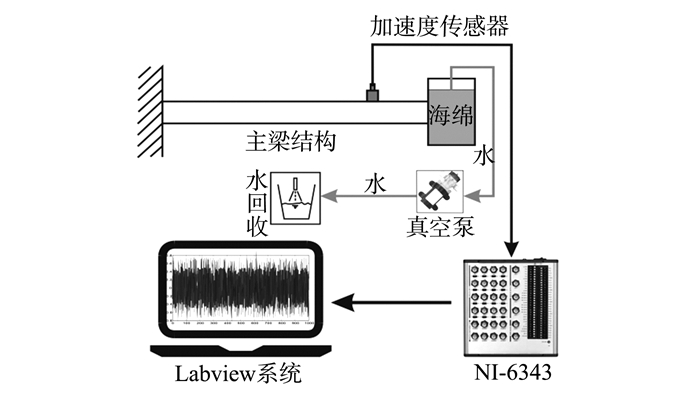
为了验证力学模型的正确性, 设计相关验证试验, 试验流程图和相应的测试平台分别如图 5、6所示。被测系统为铝合金悬臂梁和变质量附件组合结构, 通过连续改变水的质量研究质量变化对悬臂梁模态参数的影响, 为了减小水晃动对系统振动的影响, 在变质量构件处填塞了海绵。试验的关键技术为采用不同数量的真空泵实现不同的质量变化率。若使用一个真空泵时质量的变化率为Rm, 当使用2个时, 质量变化率为2Rm, 以此类推。加速度信号经过数据采集器, 在Labview中进行数据处理和信号分析。梁长宽高分别为550、50和5 mm, 弹性模量E=70 GPa, 泊松比为0.27, 密度为2 850 kg/m3。末端的质量变化率用水质量的平均变化率近似, 即dm/dt=(m2-m1)/T, m2和m1分别为两个时刻的质量, T为两个时刻的时间差。设备的具体型号为:PCB-352B10加速传感器、PCB-482C05信号调理仪、NI-6343数据采集卡以及Labview12系统。
|
图 5 试验流程图 Figure 5 Chart of experiment |
|
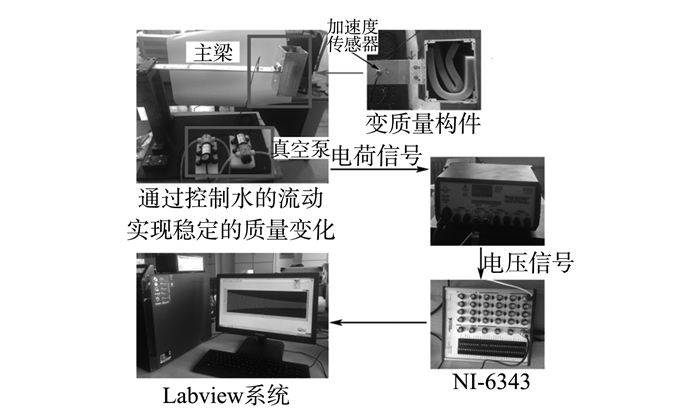
图 6 变质量时变系统动力学测试平台 Figure 6 Dynamic test platform of time varying mass system |
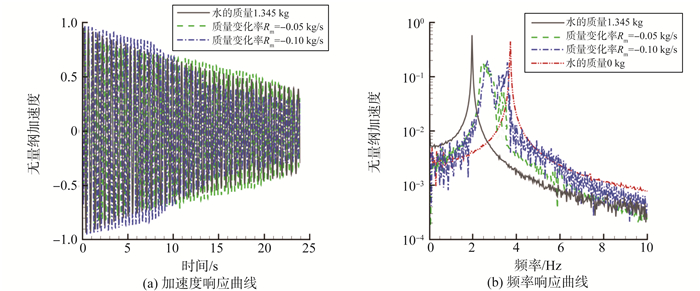
首先测量了质量减少工况时梁末端的加速度响应, 响应曲线如图 7所示。对比图 4(a)和图 7(a)可以发现试验结果和仿真结果吻合很好, 说明本研究提出的试验方法的可行性。试验中可以明显看出, 在质量减少的过程中, 系统的衰减减慢, 而且使用2个真空泵时, 系统的振动幅值在6~8 s甚至出现了一定的增大, 这说明非结构负阻尼在一定程度上超过了结构阻尼的影响。由于系统的质量随时间变化, 系统的振动频率也是变化的, 因此在频率响应曲线上, 频率是以一段连续的频率带的形式出现的, 而频率带的带宽可由系统质量的变化范围确定。
|
图 7 质量减少时梁末端的响应 Figure 7 Experimental results for decreasing mass system |
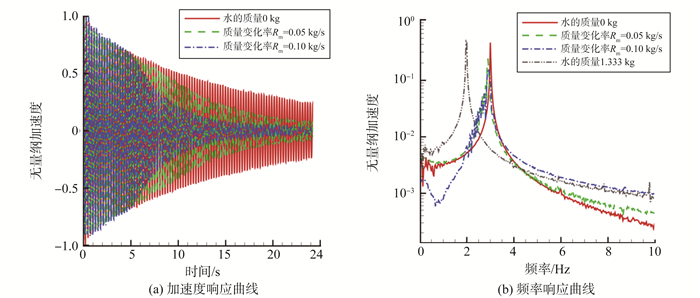
同样, 质量增加系统的试验数据如图 8所示。比较图 4(b)和图 8(a)可知, 试验结果与数值仿真结果基本一致:质量增大越快, 系统的衰减越快。在试验中也会发现, 相比较时不变系统, 时变系统的信号更加复杂, 也更容易受到干扰, 特别是在质量变化过程中, 一些噪声信号和水的晃动不可避免, 因此图 7、8中的系统响应曲线不如图 3、4中的光滑, 在以后的试验中, 应着重减少噪声影响, 提高测量精度。
|
图 8 质量增加时系统的响应曲线 Figure 8 Experimental results for increasing mass system |
仿真与试验结果表明, 时变系统的振动响应信号是典型的非平稳信号, 虽然通过傅里叶分析可以得到振动信号的频率成分和这些频率成分对应的幅值和相位, 但是无法反映这些频率成分对应的时间特性。如图 7(b)和图 8(b)中, 虽然能得到系统振动频率的变化范围, 但是无法确定该频率出现的时间和工况。这是由于傅里叶变换缺乏频率和时间的定位功能, 在分辨率上对非平稳信号分析具有一定的局限性[24]。而时频分析作为一种新兴的信号处理方法, 近年来在非线性动力学、电力系统分析、故障诊断和时变结构模态参数识别等领域得到了广泛应用[24-25]。借助时频分析技术, 能够得到任意时刻的瞬时频率及其振动能量, 并且能够进行时频滤波和时变信号的研究, 从而更加全面地分析时变系统的振动特性。
Choi-Williams时频分布(Choi-Williams distribution, CWD)是一种常用的Cohen类时频分布函数, 具有很好的时频聚集性[26], 凭借其优良的时变特性和较高的时频分辨率一直应用于非平稳信号的分析和处理领域, 该分布函数通过双线性组合表示:
| $ {\rm{C}}{{\rm{W}}_x}\left( {t,\omega } \right) = \sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} \int {\int_{ + \infty }^{ - \infty } {\frac{\sigma }{{\left| \tau \right|}}\exp \left( { - 2{\sigma ^2}{{\left( {s - t} \right)}^2}/{\tau ^2}} \right)x\left( {s + \frac{\tau }{2}} \right){x^ * }\left( {s + \frac{\tau }{2}} \right)\exp \left( { - {\rm{j}}2{\rm{ \mathsf{ π} }}\omega \tau } \right){\rm{d}}s{\rm{d}}\tau } ,} $ | (17) |
式中:x(s+τ/2)为时域测量信号; *表示复共轭函数; σ>0为一个尺度控制因子, 用来控制信号分析时的整体平滑度。
根据公式(17), 对图 7(a)中的加速度响应信号开展时频变换, 可以得到系统振动在时频域上的能量密度谱图, 如图 9所示。从图 9中可以直接获取系统的振动频率随时间的变化规律, 这是傅里叶变换无法得到的。对于质量减少的情况, 系统的振动频率从2.2 Hz增加到3.5 Hz附近, 频率变化范围与图 7(b)中频响曲线中的频率范围相对应, 这说明系统振动频率的变化范围可以通过系统质量的变化范围确定, 使用时频分析可以到得到系统频率变化的时间规律, 特别适用于非平稳信号处理。从图 9也可以看出系统的振幅的改变, 这与系统幅值的变化对应一致。

|
图 9 质量减少时系统的时频响应谱图 Figure 9 Time-frequency spectrum for increasing mass system |
类似的, 对图 8(a)中的加速度响应信号应用Choi-Williams时频变换, 可以得到质量增加系统的时频响应谱图, 不同条件下系统信号的时频谱图如图 10所示。由图 10可知, 系统的振动频率从3.5 Hz降低到2.2 Hz左右, 同时也可以解释系统的振动能量随时间的变化规律。综上所述, 采用时频分析技术分析变质量时变系统的非平稳信号, 可以更加全面准确的分析系统的振动特征。

|
图 10 质量增加时系统的时频响应谱图 Figure 10 Time-frequency spectrum for increasing mass system |
针对变质量作用下的机械臂结构建立系统的简化力学模型, 推导了变质量系统的运动方程, 使用自适应Newmark法计算了系统的响应, 并设计变质量-弹性结构振动测试试验, 从理论和试验两个方面开展了质量时变结构的动力学特性分析, 得到以下结论:
(1) 试验结果与数值仿真对应一致, 验证了本研究建模方法和试验设计的正确性。
(2) 使用自适应Newmark法求解时变参数系统的动力学响应, 收敛快, 精度高。
(3) 质量变化使得系统振动频率变化的同时, 会引起一个非结构阻尼, 该非结构阻尼与质量变化率成正比。当系统质量增加时, 会引起一个正阻尼; 当系统质量减少时, 引起一个负阻尼, 该非结构负阻尼会减慢系统振动的衰减, 当质量快速减少时, 附加负阻尼的作用可能会超过系统结构阻尼的作用, 引起系统振动幅值的增大。
(4) 使用时频分析技术, 可以给出系统的系统振动频率随时间的变化规律和系统振动能量的变化谱图, 使用简单, 准确率高, 是处理变质量系统响应信号的一种有效手段。
| [1] | 杨来伍, 梅凤翔. 变质量系统动力学[M]. 北京: 北京理工大学出版社, 1989. |
| [2] |
孙焕纯, 宋亚新, 张典仁. 变质量变阻尼变刚度结构系统的动力响应[J].
计算结构力学及其应用, 1996, 13(2): 127-137 SUN Huanchun, SONG Yaxin, ZHANG Dianya. A method for analyzing the dynamic response of a structural system with variable mass damping and stiffness[J]. Computational Structural Mechanics and Applications, 1996, 13(2): 127-137 |
| [3] |
陈占清, 缪协兴, 荆武兴. 变质量挠性体动力学普遍方程(1)[J].
湘潭大学自然科学学报, 2001, 23(4): 56-59 CHEN Zhanqing, MIAO Xiexing, JING Wuxing. Universal dynamic equations for flexiable body with variable mass(Ⅰ)[J]. Natural Science Journal of Xiangtan University, 2001, 23(4): 56-59 DOI:10.3969/j.issn.1000-5900.2001.04.012 |
| [4] |
缪协兴, 陈占清, 荆武兴. 变质量挠性体动力学普遍方程(二)[J].
哈尔滨工业大学学报, 2001, 33(6): 736-739 MIAO Xiexing, CHEN Zhanqing, JING Wuxing. Universal dynamic equations for flexiable body with variable mass(Ⅱ)[J]. Journal of Harbin Engineering University, 2001, 33(6): 736-739 DOI:10.3321/j.issn:0367-6234.2001.06.004 |
| [5] |
张耀良, 朱卫兵. 变质量非完整系统Hamilton正则方程的积分因子和守恒定理[J].
哈尔滨工程大学学报, 2002, 23(4): 118-121 ZHANG Yaoliang, ZHU Weibing. Integrating factors and conservation theorems for Hamilton's canonicals equations of motion of variable mass nonholonomic nonconservative dynamical systems[J]. Journal of Harbin Engineering University, 2002, 23(4): 118-121 DOI:10.3969/j.issn.1006-7043.2002.04.027 |
| [6] |
朱岩, 王树林. 一类变质量振动系统的近似求解[J].
振动与冲击, 2008, 27(11): 160-162, 167, 206 ZHU Yan, WANG Shulin. Analytical solution for vibration system with time varying mass[J]. Journal of vibration and shock, 2008, 27(11): 160-162, 167, 206 DOI:10.3969/j.issn.1000-3835.2008.11.037 |
| [7] | KALYONCU M, BOTSALI F M. Vibration analysis of an elastic robot manipulator with prismatic joint and a time-varying end mass[J]. Arabian Journal for Science and Engineering, 2004, 29(1): 27-38 |
| [8] | NHLEKO S. Free vibration states of an oscillator with a linear time-varying mass[J]. Journal of Vibration and Acoustics, 2009, 131(5): 051011-1-8 |
| [9] | MACIEJEWSKI I, MEYER L, KRZYZYNSKI T. The vibration damping effectiveness of an active seat suspension system and its robustness to varying mass loading[J]. Journal of Sound and Vibration, 2010, 329(19): 3898-3914 DOI:10.1016/j.jsv.2010.04.009 |
| [10] | CVETICANIN L. Van der Pol oscillator with time variable parameters[J]. Acta Mechanica, 2013, 224(5): 945 DOI:10.1007/s00707-012-0785-y |
| [11] | CVETICANIN L. Dynamics of bodies with time-variable mass[M]. Cham (ZG), Switzerland: Springer International Publishing, 2016. |
| [12] | RICHARDS J A. Analysis of periodically time-varying systems[M]. Springer-Verlag Berlin Heidelberg: Springer Science & Business Media, 2012. |
| [13] | VAN HORSSEN W T, PISCHANSKYY O V, DUBBELDAM J L A. On the forced vibrations of an oscillator with a periodically time-varying mass[J]. Journal of Sound and Vibration, 2010, 329(6): 721-732 DOI:10.1016/j.jsv.2009.10.001 |
| [14] | PISCHANSKYY O V, VAN HORSSEN W T. On the nonlinear dynamics of a single degree of freedom oscillator with a time-varying mass[J]. Journal of Sound and Vibration, 2012, 331(8): 1887-1897 DOI:10.1016/j.jsv.2011.12.009 |
| [15] | ABRAMIAN A K, VAN HORSSEN W T, VAKULENKO S A. Nonlinear vibrations of a beam with time-varying rigidity and mass[J]. Nonlinear Dynamics, 2013, 71(1-2): 291-312 DOI:10.1007/s11071-012-0661-2 |
| [16] |
王宇楠, 邢誉峰. 变质量梁的自适应Newmark法[J].
北京航空航天大学学报, 2014, 40(6): 829-833 WANG Yu'nan, XING Yufeng. Self-adaptive Newmark method of variable-mass beam dynamic system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(6): 829-833 |
| [17] | ZHAO Rui, YU Kaiping. Hamilton's law of variable mass system and time finite element formulations for time-varying structures based on the law[J]. International Journal for Numerical Methods in Engineering, 2014, 99(10): 711-736 DOI:10.1002/nme.v99.10 |
| [18] | MAZENC F, MALISOFF M, NICULESCU S I. Reduction model approach for linear time-varying systems with delays[J]. IEEE Transactions on Automatic Control, 2014, 59(8): 2068-2082 DOI:10.1109/TAC.2014.2320308 |
| [19] |
杜妍辰, 高雷, 周燕瑜, 等. 变质量振动系统的求解与分析[J].
上海理工大学学报, 2015, 5(5): 462-466 DU Yanchen, GAO Lei, ZHOU Yanyu, et al. Solution and analysis of vibration system with variable mass[J]. Journal of University of Shanghai for Science and Technology, 2015, 5(5): 462-466 |
| [20] | 于开平. 变质量航天器结构动响应分析[M]. 西安: 中国力学大会, 2013: 119-119. |
| [21] | FLORES J, SOLOVEY G, GILL S. Variable mass oscillator[J]. American Journal of Physics, 2003, 71(7): 721-725 DOI:10.1119/1.1571838 |
| [22] |
舒俊成. 变质量SD振子动力学分析与试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
SHU Juncheng. Dynamical analysis and experiment of variable mass SD oscillator[D]. Harbin: Harbin Institute of Technology, 2016. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D01099547 |
| [23] | BARTKOWIAK T, GRABSKI J K, KOŁODZIEJ J A. Numerical and experimental investigations of the dynamics of a variable mass pendulum[J]. Proceedings of the Institution of Mechanical Engineers:Part C: Journal of Mechanical Engineering Science, 2016, 230(12): 2124-2132 DOI:10.1177/0954406215590454 |
| [24] | 科恩L. 时-频分析: 理论与应用[M]. 白居宪, 译. 西安: 西安交通大学出版社, 1998. |
| [25] |
李小彭, 姚红良, 任朝晖, 等. 时频分析在质量慢变碰摩转子系统中的应用[J].
机械制造, 2005, 43(10): 20-22 LI Xiaopeng, YAO Hongliang, REN Chaohui, et al. Application of time frequency analysis for a slow-varying rotor system with rubbing fault[J]. Machinery, 2005, 43(10): 20-22 |
| [26] |
马驰骋, 张希农, 柳征勇, 等. 变质量贮箱类流固耦合系统的振动响应及时频特性分析[J].
振动与冲击, 2014, 33(21): 166-17 MA Chicheng, ZHANG Xinong, LIU Zhengyong, et al. Dynamic responses and time-frequency feature analysis for a fluid-structure coupling system with avariable mass tank[J]. Journal of Vibration and Shock, 2014, 33(21): 166-17 |



