混沌同步取得了很多成果[1-12], 而随着分数阶微积分的发展, 众多学者开始研究分数阶混沌系统的同步问题。例如:文献[13]研究了分数阶混沌系统的主动滑模控制, 给出了滑模切换函数的构造; 文献[14]研究了分数阶复杂网络系统的混合投影同步; 文献[15]研究了一类分数阶双曲混沌系统的自适应脉冲同步; 文献[16]研究了一类分数阶自适应滤波有限时间混沌同步。混沌同步及其应用越来越广泛应用于其它交叉学科, 20世纪90年代, 混沌理论应用于生物医学等交叉边缘学科, 极大推动了这些学科的发展, 如神经系统、心脑血管系统等生物医药学科, 一些心脑血管疾病的探索与诊治取得了很大进步, 血管痉挛是引起心脑血管疾病的主要原因, 血管一旦进入混沌状态会导致血管痉挛等心脑血管疾病的发生。因此了解冠状动脉系统的混沌同步显得尤为重要。文献[17]研究了肌型血管生物数学模型的自适应Backstepping控制设计问题, 给出了冠状动脉系统的生物数学模型。文献[18]研究了冠状动脉系统高阶滑模自适应混沌同步设计问题。上述研究考虑的都是整数阶冠状动脉系统, 而分数阶冠状动脉系统模型更接近于实际系统, 在上述研究的基础上, 本研究分析了一类分数阶冠状动脉系统的混沌同步问题, 基于Lyapunov稳定性理论给出了系统取得同步的3个充分性条件, 结果表明在适当的选取控制律下, 系统取得混沌同步。
1 系统描述及预备知识冠状动脉系统加上周期性刺激可化简为如下生物数学模型[18]:
| $ \left\{ \begin{array}{l} \dot x = - bx - cy\\ \dot y = - \lambda \left( {1 + b} \right)x - \lambda \left( {1 + c} \right)y + \lambda {x^3} + E\cos \omega t' \end{array} \right. $ | (1) |
式中:x为冠状动脉血管内径变化量; y为血管内壁的压力差; a, b, c, λ为常值参数; E cos (ωt)是冠状动脉受到的周期性刺激, 其中E为振幅, ω为角速度, t为时间。
定义1[19] Caputo分数阶导数定义为
| $ {}_c{\rm{D}}_{{t_0},t}^\alpha = {\rm{D}}_{{t_0},t}^{ - \left( {n - \alpha } \right)}\frac{{{{\rm{d}}^n}}}{{{\rm{d}}{t^n}}}x\left( t \right) = \frac{1}{{{\Gamma }\left( {n - \alpha } \right)}}\int_{{t_0}}^t {{{\left( {t - \tau } \right)}^{n - \alpha - 1}}{x^{\left( n \right)}}\left( \tau \right){\rm{d}}\tau } ,n - 1 < \alpha < n \in {{\bf{Z}}^ + }。$ |
定义2[20] 单参数Mittag-Leffler函数
| $ {E_\alpha }\left( z \right) = \sum\limits_{k = 1}^\infty {\frac{{{z^k}}}{{{\rm{\Gamma }}\left( {k\alpha + 1} \right)}}} ,\alpha > 0,z \in C。$ |
定义3[20] 双参数Mittag-Leffler函数
| $ {E_{\alpha ,\beta }}\left( z \right) = \sum\limits_{k = 1}^\infty {\frac{{{z^k}}}{{{\rm{\Gamma }}\left( {k\alpha + \beta } \right)}}} ,\alpha ,\beta > 0,有\;{E_\alpha }\left( z \right) = {E_{\alpha ,1}}\left( z \right),{E_{1,1}}\left( z \right) = {e^z}。$ |
引理1[20] 若α<2, β∈∀R, πα/2<ρ<min{π, πα}, 则存在实常数C满足
| $ \left| {{E_{\alpha ,\beta }}\left( z \right)} \right| \le \frac{C}{{1 + \left| z \right|}},\;\;\;\rho \le \left| {\arg \left( z \right)} \right| \le {\rm{ \mathsf{ π} }},\left| z \right| > 0。$ |
引理2[21] 若V(t)是[0, ∞)上的连续函数, 满足DtαV(t)≤-ηV(t), 则有:V(t)≤V(t0)Eα(-η(t-t0)α), 其中α∈(0, 1), η>0为常数。
2 控制方案一分数阶冠状动脉系统模型的驱动系统为
| $ \left\{ \begin{array}{l} {\rm{D}}_t^\alpha {x_1} = - b{x_1} - c{y_1}\\ {\rm{D}}_t^\alpha {y_1} = - \lambda \left( {1 + b} \right){x_1} - \lambda \left( {1 + c} \right){y_1} + \lambda x_1^3 + E\cos \omega t \end{array} \right., $ | (2) |
响应系统设计为
| $ \left\{ \begin{array}{l} {\rm{D}}_t^\alpha {x_2} = - b{x_2} - c{y_2}\\ {\rm{D}}_t^\alpha {y_2} = - \lambda \left( {1 + b} \right){x_2} - \lambda \left( {1 + c} \right){y_2} + \lambda x_2^3 + E\cos \omega t + u\left( t \right) \end{array} \right., $ | (3) |
定义系统误差
| $ {e_1} = {x_2} - {x_1},{e_2} = {y_2} - {y_1}, $ | (4) |
则得到误差系统方程为
| $ \left\{ \begin{array}{l} {\rm{D}}_t^\alpha {e_1} = - b{e_1} - c{e_2}\\ {\rm{D}}_t^\alpha {e_2} = - \lambda \left( {1 + b} \right){e_1} - \lambda \left( {1 + c} \right){e_2} + \lambda x_2^3 - \lambda x_1^3 + u\left( t \right) \end{array} \right.。$ | (5) |
定理1 设计u(t)=bεe1+cεe2+λ(1+b)e1+λ(1+c)e2-λ(x23-x13)-η sgn (s(t)), 其中η为大于0的常数, 则系统(2)与(3)是滑模混沌同步的。
证明 设计滑模面函数s(t)=Dtα-1e2(t)-εDtα-1e1(t), 其中ε为常数。当系统(5)在滑模面上运动时, 必然满足滑动模方程:s(t)=0,
| $ - b\varepsilon {e_1} - c\varepsilon {e_2} - \lambda \left( {1 + b} \right){e_1} - \lambda \left( {1 + c} \right){e_2} + \lambda \left( {x_2^3 - x_1^3} \right) + u\left( t \right) = 0, $ |
所以设计等效控制系统
| $ {u_{{\rm{eq}}}} = b\varepsilon {e_1} + c\varepsilon {e_2} + \lambda \left( {1 + b} \right){e_1} + \lambda \left( {1 + c} \right){e_{2 }} - \lambda \left( {x_2^3 - x_1^3} \right), $ |
设计切换控制系统
| $ \begin{array}{*{20}{c}} {{u_{{\rm{sw}}}} = - \eta {\mathop{\rm sgn}} \left( {s\left( t \right)} \right),}&{u\left( t \right) = {u_{{\rm{eq}}}} + {u_{{\rm{sw}}}}} \end{array}, $ |
构造Lyapunov函数
| $ V\left( t \right) = \frac{1}{2}{s^2}\left( t \right), $ |
求导得到:
| $ \begin{array}{l} \dot V\left( t \right) = s\dot s = s\left[ { - b\varepsilon {e_1} - c\varepsilon {e_2} - \lambda \left( {1 + b} \right){e_1} - \lambda \left( {1 + c} \right){e_2} + \lambda \left( {x_2^3 - x_1^3} \right) + u\left( t \right)} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\; - \eta s\left( t \right){\mathop{\rm sgn}} \left( {s\left( t \right)} \right) = - \eta \left| {s\left( t \right)} \right| < 0。\end{array} $ |
定理2 设计u(t)=λ(1+b)e1+λ(1+c)e2-λ(x23-x13)-be2+c sgn(e2)sgn(e1)e2, 则系统(2)与(3)是混沌同步的。
证明 构造Lyapunov函数
| $ V\left( t \right) = \left| {{e_1}\left( t \right)} \right| + \left| {{e_2}\left( t \right)} \right|, $ |
则有:
| $ \begin{array}{l} {\rm{D}}_t^\alpha V\left( t \right) = {\rm{D}}_t^\alpha \left[ {\left| {{e_1}\left( t \right)} \right| + \left| {{e_2}\left( t \right)} \right|} \right] = {\mathop{\rm sgn}} \left( {{e_1}\left( t \right)} \right){\rm{D}}_t^\alpha {e_1}\left( t \right) + \\{\mathop{\rm sgn}} \left( {{e_2}\left( t \right)} \right){\rm{D}}_t^\alpha {e_2}\left( t \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathop{\rm sgn}} \left( {{e_1}} \right)\left( { - b{e_1} - c{e_2}} \right) + {\mathop{\rm sgn}} \left( {{e_2}} \right)\left[ {1 - \lambda \left( {1 + b} \right){e_1} - \lambda \left( {1 + c} \right){e_2} +\\ \lambda \left( {x_2^3 - x_1^3} \right) + u} \right]。\end{array} $ |
由于e2(t)sgn(e2(t))=|e2(t)|, e2(t)≠0时, sgn(e2(t))sgn(e2(t))=1⇒DtαV(t)=-b(|e1|+|e2|)=-bV(t)。
根据引理2很容易得到:
| $ \mathit{V}\left( t \right) \le \mathit{V}\left( {{t_0}} \right){E_\alpha }\left( { - b{{\left( {t - {t_0}} \right)}^\alpha }} \right), $ |
| $ \mathit{V}\left( t \right) = \left| {{e_1}\left( t \right)} \right| + \left| {{e_2}\left( t \right)} \right|,V\left( {{t_0}} \right) = \left| {{e_1}\left( {{t_0}} \right)} \right| + \left| {{e_2}\left( {{t_0}} \right)} \right|。$ |
令z=-b(t-t0)α, |arg(z)|=π, 根据引理1, 存在常数C使得:
| $ \left\| {\mathit{V}\left( t \right)} \right\| \le \frac{{C\left\| {\mathit{V}\left( {{t_0}} \right)} \right\|}}{{1 + \left| { - b{{\left( {t - {t_0}} \right)}^\alpha }} \right|}} \Rightarrow t \to \infty ,\left\| {\mathit{V}\left( t \right)} \right\| \to 0 \Rightarrow \left\| {{e_i}\left( t \right)} \right\|\left( {i = 1,2} \right) \to 0。$ |
设计分数阶冠状动脉系统作为主系统
| $ \left\{ \begin{array}{l} {\rm{D}}_t^\alpha {x_1} = - b{x_1} - c{x_2}\\ {\rm{D}}_t^\alpha {x_2} = - \lambda \left( {1 + b} \right){x_1} - \lambda \left( {1 + c} \right){x_2} + \lambda x_1^3 + E\cos \omega t \end{array} \right., $ | (6) |
其从系统设计为
| $ \left\{ \begin{array}{l} {\rm{D}}_t^\alpha {y_1} = - b{y_1} - c{y_2}\\ {\rm{D}}_t^\alpha {y_2} = - \lambda \left( {1 + b} \right){y_1} - \lambda \left( {1 + c} \right){y_2} + \lambda y_1^3 + E\cos \omega t + \Delta g\left( {{y_1},{y_2}} \right) + d\left( t \right) + u\left( t \right) \end{array} \right.。$ | (7) |
假设1 存在正常数m, n>0, 使得|Δg(y1, y2)|<m, |d(t)|<n。
定义误差ei=yi-xi(i=1, 2), 则误差系统为
| $ \left\{ \begin{array}{l} {\rm{D}}_t^\alpha {e_1} = - b{e_1} - c{e_2}\\ {\rm{D}}_t^\alpha {e_2} = - \lambda \left( {1 + b} \right){e_1} - \lambda \left( {1 + c} \right){e_2} + \lambda y_1^3 - \lambda x_1^3 + \Delta g\left( {{y_1},{y_2}} \right) + d\left( t \right) + u\left( t \right) \end{array} \right.。$ | (8) |
针对误差系统(3)设计非奇异终端滑模面
| $ s\left( t \right) = {\rm{D}}_t^{2\alpha - 1}{e_1}\left( t \right) + \lambda \int_0^t {{{\left| {{\rm{D}}_t^{\alpha - 1}{e_2}\left( \tau \right)} \right|}^r}{\mathop{\rm sgn}} \left( {{\rm{D}}_t^{\alpha - 1}{e_2}\left( \tau \right)} \right){\rm{d}}\tau } 。$ | (9) |
定理3 误差系统(8)在非奇异滑模面(9)上, 系统(8)的轨迹在有限时间内到达平衡点。
证明 误差系统满足滑模面方程
| $ {s_i}\left( t \right) = 0,{{\dot s}_i}\left( t \right) = 0, $ |
于是有
| $ {\rm{D}}_t^{2\alpha }{e_1}\left( t \right) = {\rm{D}}_t^\alpha {e_2}\left( t \right) = - \lambda {\left| {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right|^r}{\mathop{\rm sgn}} \left( {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right)。$ |
选取Lyapunov函数
| $ V\left( t \right) = \frac{1}{2}{\left( {D_t^{\alpha - 1}{e_2}\left( t \right)} \right)^2}, $ |
则
| $ \dot V = {\rm{D}}_t^{\alpha - 1}{e_2} \cdot {\rm{D}}_t^\alpha {e_2} = - \lambda {\left| {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right|^r} \cdot {\mathop{\rm sgn}} \left( {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right){\rm{D}}_t^{\alpha - 1}{e_2} =\\ - \lambda {\left| {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right|^{r + 1}} < 0。$ |
设计新型双幂次趋近律来设计控制律
| $ \begin{array}{l} u\left( t \right) = \lambda \left( {1 + b} \right){e_1} + \lambda \left( {1 + c} \right){e_2} - \lambda y_1^3 + \lambda x_1^3 - \left( {m + n} \right){\mathop{\rm sgn}} \left( s \right) - \\ \;\;\;\;\;\;\;\;\;\lambda {\left| {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right|^r} \cdot {\mathop{\rm sgn}} \left( {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right) - \left( {{k_1}{{\left| s \right|}^\gamma } + {k_2}{{\left| s \right|}^\mu }} \right){\mathop{\rm sgn}} \left( s \right), \end{array} $ | (10) |
式中:k1>0, k2>0, γ>1, 0<μ<1。
定理4 在控制器(10)的作用下, 误差系统(8)的状态轨迹能达到滑模面。
证明 选择Lyapunov函数V(t)=
| $ \begin{array}{l} \dot V = s\left[ {{\rm{D}}_t^\alpha {e_2}\left( t \right) + \lambda {{\left| {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right|}^r}{\mathop{\rm sgn}} \left( {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right)} \right] = \\ \;\;\;\;\;\;s\left[ { - \lambda \left( {1 + b} \right){e_1} - \lambda \left( {1 + c} \right){e_2} + \lambda y_1^3 - \lambda x_1^3 + \Delta g\left( {{y_1},{y_2}} \right) + } \right.\\ \;\;\;\;\;\;\left. {d\left( t \right) + u\left( t \right) + \lambda {{\left| {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right|}^r}{\mathop{\rm sgn}} \left( {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right)} \right], \end{array} $ |
由假设条件1可得:
| $ \begin{array}{l} \dot V \le s\left( {\Delta g\left( {{y_1},{y_2}} \right) + d\left( t \right)} \right) - \left( {m + n} \right)\left| {{s_1}} \right| - \left( {{k_1}{{\left| s \right|}^{\gamma + 1}} + {k_2}{{\left| s \right|}^{\mu + 1}}} \right) \le \\ \;\;\;\;\;\; - \left( {{k_1}{{\left| s \right|}^{\gamma + 1}} + {k_2}{{\left| s \right|}^{\mu + 1}}} \right) < 0。\end{array} $ |
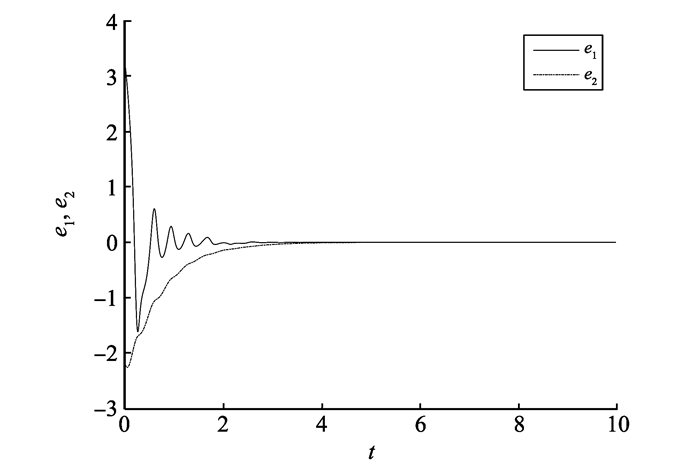
以分数阶冠状动脉系统(2)(3)为例, 当α=0.93, b=0.15, c=-1.7, λ=-0.65, E=0.3, ω=1时系统呈现混沌态, 系统的初始状态设置为:(x1(0), x2(0))=(-2.2, 1.1), (y1(0), y2(0))=(1, -1.1), 选取定理1中的滑模控制器, 定理1中系统的误差响应曲线如图 1所示, 方案一采用滑模控制能够消除系统的不确定性和非线性, 从而达到良好的控制效果, 当系统取得混沌同步时, 就会避免出现冠状动脉血管痉挛现象, 从而能够避免出现冠心病等心脑血管疾病的发生。
|
图 1 定理1中的系统误差曲线 Figure 1 The system curvers of theorem 1 |
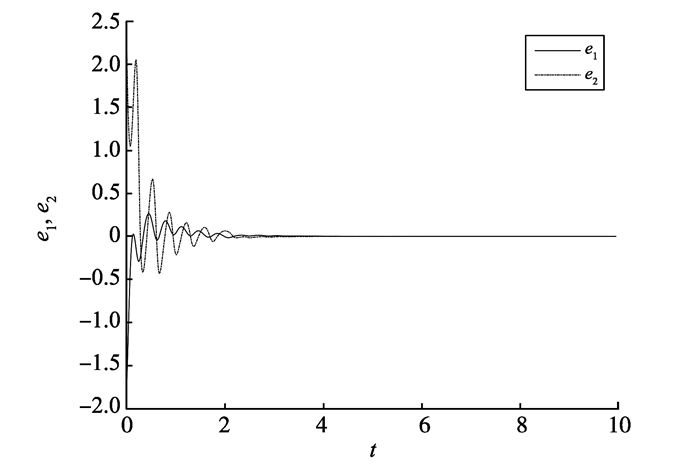
选取系统初始状态(x1(0), x2(0))=(0.7, -1.5), (y1(0), y2(0))=(-1, 0.7), 以及定理2中的控制器, 定理2中的系统误差曲线如图 2所示。
|
图 2 定理2中的系统误差曲线 Figure 2 The system curvers of theorem 2 |
方案二采用的Lyapunov函数相对简略, 在控制器的选取上也显得干练, 最终能实现混沌同步, 与第一种方法相比, 该种方法的控制效果可能会显得稍差一些, 表现在取得同步的时间会稍长一些。从医学角度讲就是由冠状动脉血管痉挛到正常的持续时间较长, 病人需要忍受更长时间的心绞疼等病痛的折磨。
控制方案三中以系统(6)(7)为例, Δg=-0.05sin y1, d(t)=0.2cos(t), (x1(0), x2(0))=(0.1, 0.2), (y1(0), y2(0))=(0.5, -0.6), r=1.5, λ=6, k1=10, k2=4, γ=2, μ=0.5, α=0.93, 设计非奇异终端滑模面
| $ s\left( t \right) = {\rm{D}}_t^{2\alpha - 1}{e_1}\left( t \right) + \lambda \int_0^t {{{\left| {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right|}^r}{\mathop{\rm sgn}} \left( {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right){\rm{d}}\tau } , $ |
用双幂次趋近律
| $ \begin{array}{l} u\left( t \right) = \lambda \left( {1 + b} \right){e_1} + \lambda \left( {1 + b} \right){e_2} - \lambda y_1^3 + \lambda x_1^3 - \left( {m + n} \right){\mathop{\rm sgn}} \left( s \right) - \\ \;\;\;\;\;\;\;\;\;\lambda {\left| {{\rm{D}}_t^{2\alpha - 1}{e_2}\left( t \right)} \right|^r} \cdot {\mathop{\rm sgn}} \left( {{\rm{D}}_t^{\alpha - 1}{e_2}\left( t \right)} \right) - \left( {{k_1}{{\left| s \right|}^\gamma } + {k_2}{{\left| s \right|}^\mu }} \right){\mathop{\rm sgn}} \left( s \right), \end{array} $ |
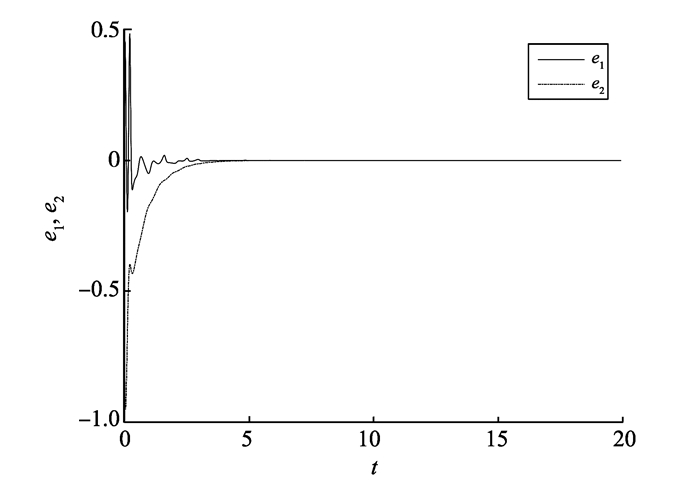
该趋近律收敛速度较快, 其系统的误差曲线如图 3所示。
|
图 3 系统的误差曲线 Figure 3 The errors of systems |
方案三采用的是滑模控制且选取的是双幂次滑模趋近律, 能够避免出现高频抖震和震颤, 当系统取得混沌同步时表现为血管内壁承受的压力趋于平稳和正常水平, 不会出现突然流速急剧加快的情形, 从医学上讲就会避免出现心悸和心绞疼等现象的发生, 且系统从混沌到同步的时间较短, 从医学上讲病人承受的冠状动脉血管痉挛的时间较短, 很快趋于正常水平, 能够为病人减轻痛苦, 这在临床疗效上是可取的。
6 结语利用滑模同步控制研究方法, 本研究分析了一类分数阶冠状动脉系统的混沌同步问题, 给出了系统取得同步的三个充分性条件, 结论表明在适当的选取控制律下, 系统取得混沌同步。如何将该结论在医学中加以推广和应用以及考虑冠状动脉系统的有限时间滑模同步问题是下一步亟需解决的课题。
| [1] | YASSEN M T. Controlling chaos and synchronization for new chaotic system using linear feedback control[J]. Chaos, Solition & Fractals, 2005, 26(3): 913-920 |
| [2] | CHEN M, CHEN W. Robust adaptive neural network synchronization controller design for a class of time delay uncertain chaotic systems[J]. Chaos, Solition & Fractals, 2009, 41(5): 2716-2724 |
| [3] | PECORA L M, CAROLL T L. Synchronization in chaotic systems[J]. Physics Review Letters, 1990, 64(8): 821-824 DOI:10.1103/PhysRevLett.64.821 |
| [4] | WU X J, LU H T. Adaptive generalized function projective lag synchronization of different chaotic systems with fully uncertain parameters[J]. Chaos, Solition & Fractals, 2011, 44(10): 820-810 |
| [5] | SALARIEH H, ALASTY A. Adaptive synchronization of two chaotic systems with stochastic unknown parameters[J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(2): 508-519 DOI:10.1016/j.cnsns.2007.09.002 |
| [6] | SUN Y P, LI J M, WANG J A, et al. Generalized projective synchronization of chaotic systems via adaptive learing control[J]. Chinese Physics B, 2010, 19(2): 502-505 |
| [7] | YANG L, YANG J. Robust finite-time convergence of chaotic systems via adaptive terminal sliding mode scheme[J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(6): 2405-2413 DOI:10.1016/j.cnsns.2010.09.022 |
| [8] | AGHABABA M P, AKBARI M E. A chattering-free robust adaptive sliding mode controller for synchronization of two different chaotic systems with unknown uncertainties and external disturbances[J]. Applied Mathematics and Computation, 2012, 218(9): 5757-5768 DOI:10.1016/j.amc.2011.11.080 |
| [9] | AGHABABA M P, HEYDARI A. Chaos synchronization between two different chaotic systems with uncertainties, external disturbances, unknown parameters and input nonlinearities[J]. Applied Mathematical Modlling, 2012, 36(4): 1639-1652 DOI:10.1016/j.apm.2011.09.023 |
| [10] | LIU P, LIU S. Robust adaptive full state hybrid synchronization of chaotic complex systems with unkown parameters and external disturbances[J]. Nonlinear Dynamics, 2012, 70(1): 585-599 |
| [11] |
毛北行. 两类分数阶系统的观测器同步[J].
吉林大学学报(理学版), 2017, 55(1): 139-144 MAO Beixing. Observer synchronization of two kinds of fractional-order systems[J]. Journal of Jiling University (Science Edition), 2017, 55(1): 139-144 |
| [12] |
毛北行, 李巧利. 一类分数阶Genesio-Tesi系统分的滑模混沌同步[J].
中山大学学报(自然科学版), 2017, 56(2): 76-79 MAO Beixing, LI Qiaoli. Sliding mode chaos synchronization of a class of fractional-order Genesio-Tesi systems[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2017, 56(2): 76-79 |
| [13] |
孙宁, 张化光, 王智良. 不确定分数阶混沌系统的滑模投影同步[J].
浙江大学学报(工学版), 2010, 44(7): 1288-1291 SUN Ning, ZHANG Huaguang, WANG Zhiliang. Projective synchronization of uncertain fractional order chaotic system using sliding mod econtroller[J]. Journal of Zhejiang University(Engineering Science), 2010, 44(7): 1288-1291 DOI:10.3785/j.issn.1008-973X.2010.07.010 |
| [14] |
仲启龙, 邵永辉, 郑永爱. 分数阶混沌系统的主动滑模同步[J].
动力学与控制学报, 2015, 13(1): 18-22 ZHONG Qilong, SHAO Yonghui, ZHENG Yongai. Synchronization of the fractional order chaotic systems based on TS models[J]. Journal of Dynanics and Control, 2015, 13(1): 18-22 |
| [15] | XI Huiling, YU Simin, ZHANG Ruixia, et al. Adaptive impulsive synchronization for a class of fractional-order chaotic and hyperchaotic systems[J]. Optik Optics, 2014(125): 2036-2040 |
| [16] | TRAN Xuan Toa, KANG Hee Jun. Robust adaptive chatter-free finite-time control method for chaos control and (anti-)synchronization of uncertain (hyper)chaotic systems[J]. Nolinear Dynamics, 2015(80): 637-651 |
| [17] |
贡崇颖, 李医民, 孙曦浩. 肌型血管生物数学模型的自适应Backstepping控制设计[J].
生物数学学报, 2007, 22(3): 503-508 GONG Chongying, LI Yimin, SUN Xihao. Adaptive Backstepping control of the biomathematical model of muscular blood vessel[J]. Journal of Biomathematics, 2007, 22(3): 503-508 DOI:10.3969/j.issn.1001-9626.2007.03.016 |
| [18] |
赵占山, 张静, 丁刚, 等. 冠状动脉系统高阶滑模自适应混沌同步设计[J].
物理学报, 2015, 64(21): 5081-5088 ZHAO Zhanshan, ZHANG Jing, DING Gang, et al. Self-adaptive slding mode chaos synchronization of high-order coronary artery systems[J]. Acta Phyis, 2015, 64(21): 5081-5088 |
| [19] | POD LUBN Y. Fractional differential equation[M]. San Diego, CA, USA: Academic Press, 1999. |
| [20] | HILFER R. Applications of fractional calculus in physics[M]. Singapore: World Scientific York, 2000. |
| [21] | SRIVASTAVA H, OWA S. Univalent functions, fractional calculus and their applications[M]. New Jersey, USA: Prentice hall, 1989. |



