滑模同步日益成为研究的热点[1-11], 传统的滑模控制方法包括主动滑模控制[12]、自适应滑模控制[13]、终端滑模控制[14-15]。文献[16]利用比例积分追踪制导控制, 得到精确的追踪制导方法, 提出新的滑模控制方法, 即积分滑模方法; 文献[17]利用比例积分滑模方法研究新混沌系统的滑模控制问题, 提出比例积分滑模方法, 而该方面的研究还不是很多; 文献[18]提出“混沌纠缠”, 它是产生混沌的新方法, 由两个稳定的子系统通过增加纠缠项构造新混沌。该方面的研究引起控制界的密切关注[19], 而利用比例积分滑模控制研究纠缠系统混沌同步问题几乎没有该方面的报道。在上述研究的基础上, 研究新纠缠混沌系统的滑模和比例积分滑模同步问题, 设计滑模面和控制器, 给出系统取得同步的两个充分性条件。
1 系统描述考虑两个线性子系统:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = a{x_1} + b{y_1}\\ {{\dot y}_1} = b{x_1} + c{y_1} \end{array} \right., $ | (1) |
| $ {\dot z_1} = - m{z_1}, $ | (2) |
其中:(x1, y1, z1)是状态变量。当a<0, c<0, m>0两个子系统是稳定的, 通过正弦函数纠缠式(1)(2), 得到如下系统[19]
| $ \left\{ \begin{array}{l} {{\dot x}_1}{\rm{ = }}a{x_1} + b{y_1} + l\sin {y_1}\\ {{\dot y}_1} = - b{x_1} + c{y_1} + l\sin {z_1}\\ {{\dot z}_1} = - m{z_1} + l\sin {x_1} \end{array} \right., $ | (3) |
其中:a、b、c、m、l是纠缠系数;sin x1、sin y1、sin z1是纠缠函数。当a=-1, b=10, c=-1, m=3, l=18时系统(3)出现混沌吸引子, 其轨相图见图 1。
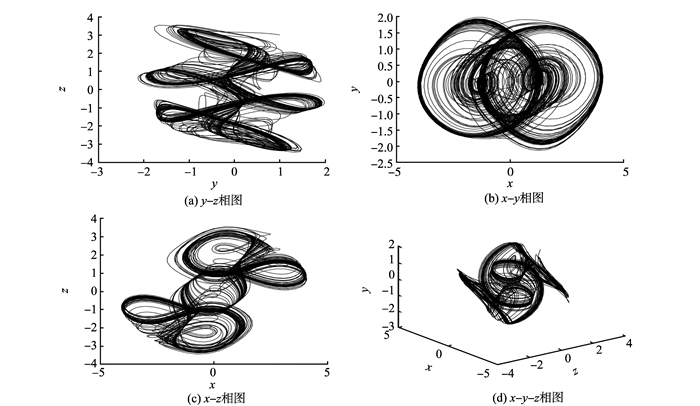
|
图 1 系统吸引子相图 Figure 1 System attractor of phase diagram |
以系统(3)作为驱动系统, 设计响应系统为
| $ \left\{ \begin{array}{l} {{\dot x}_2}{\rm{ = }}a{x_2} + b{y_2} + l\sin {y_2}\\ {{\dot y}_2} = - b{x_2} + c{y_2} + l\sin {z_2} + u\left( t \right)\\ {{\dot z}_2} = - m{z_2} + l\sin {x_2}, \end{array} \right., $ | (4) |
定义误差e1=x2-x1, e2=y2-y1, e3=z2-z1, 式(4)与式(3)相减得到
| $ \left\{ \begin{array}{l} {{\dot e}_1} = a{e_1} + b{e_2} + l\left( {\sin {y_2} - \sin {y_1}} \right)\\ {{\dot e}_2} = - b{e_1} + c{e_2} + l\left( {\sin {z_2} - \sin {z_1}} \right) + u\left( t \right)\\ {{\dot e}_3} = - m{e_3} + l\left( {\sin {x_2} - \sin {x_1}} \right) \end{array} \right.。$ | (5) |
假设1 |ae1|<|be2|。
假设2 |l(sin x2-sin x1)|<|me3|。
假设3 |be1|<|ke2|。
引理1[20] (Barbalat引理) 若函数f(t)在[0, +∞)上一致连续, 并且广义积分∫0+∞f(t)dt存在, 则有
定理1 在假设1、2条件下, 设计滑模函数s(t)=e1+e2+e3, 控制器u(t)=(b-a)e1-(b+c)e2+me3-
证明 当系统在滑模面上运动时s=0,
当不在滑模面上运动时, 构造Lyapunov函数
| $ \begin{array}{l} \dot V = s\dot s = s\left[ {{{\dot e}_1} + {{\dot e}_2} + {{\dot e}_3}} \right]\\ \;\;\; = s\left\{ {\left( {a - b} \right){e_1} + \left( {b + c} \right){e_2} - m{e_3} + l\left[( {\sin {z_2} - \sin {z_1} ) +\\ \left( {\sin {y_2} - \sin {y_1}} \right) + \left( {\sin {x_2} - \sin {x_1}} \right)} \right] + u} \right\}\\ \;\;\; \le l\left| s \right|\sum\limits_{i = 1}^3 {\left| {{e_i}} \right| - } l\sum\limits_{i = 1}^3 {\left| {{e_i}} \right|s \cdot {\mathop{\rm sgn}} \;s - \eta s \cdot {\mathop{\rm sgn}} \;s。} \end{array} $ |
根据符号函数的性质s·sgn s=|s|, 不难得到由于
以上述系统(3)作为驱动系统, 响应系统设计为式(4), 则误差系统为式(5)。选取比例积分滑模函数
| $ s\left( t \right) = {e_2}\left( t \right) + \int_0^t {\left[ {k{e_2}\left( \tau \right) + b{e_1}\left( \tau \right) - l\left( {\sin {z_2}\left( \tau \right) - \sin {z_1}\left( \tau \right)} \right)} \right]d\tau , } $ |
其中:k为可以选定的正常数, 从而有
| $ \left\{ \begin{array}{l} {{\dot e}_1} = a{e_1} + b{e_2} + l\left( {\sin {y_2} - \sin {y_1}} \right)\\ {{\dot e}_2} = - b{e_1} + k{e_2} + l\left( {\sin {z_2} - \sin {z_1}} \right)\\ {{\dot e}_3} = - m{e_3} + l\left( {\sin {x_2} - \sin {x_1}} \right) \end{array} \right.。$ | (6) |
定理2 在假设2、3下, 选取s(t)=e2(t)+∫0t[ke2(τ)+be1(τ)-l(sin z2(τ)-sin z1(τ))]dτ, 控制器u(t)=-(k+c)e2(t)-ηsgn(s(t)), 则纠缠混沌系统的主从系统(3)与(4)是比例积分滑模同步的。
证明 在滑模面上运动时, 根据理想滑模方程(6)有
不在滑模面上运动时, 选取Lyapunov函数V(t)=
| $ \begin{array}{l} \dot V\left( t \right){\rm{ = }}s\dot s = s\left[ {{{\dot e}_2}\left( t \right) + k{e_2}\left( t \right) + b{e_1}\left( t \right) - l\left( {\sin {z_2}\left( t \right) - \sin {z_1}\left( t \right)} \right)} \right]\\ \;\;\;\;\;\;\; = s\left[ { - b{e_1} + c{e_2} + l\left( {\sin {z_2} - \sin {z_1}} \right) + u\left( t \right) +\\ k{e_2}\left( t \right) + b{e_1}\left( t \right) - l\left( {\sin {z_2}\left( t \right) - \sin {z_1}\left( t \right)} \right) + u\left( t \right)} \right]\\ \;\;\;\;\;\;\; = - \eta s \cdot {\mathop{\rm sgn}} \left( s \right) = - \eta \left| {s\left( t \right)} \right| < 0, \end{array} $ |
由于
无妨利用MATLAB/simulink进行数值仿真, 系统参数a=-1, b=10, c=-1, m=3, l=18, 系统初始值设置为(x1(0), y1(0), z1(0))=(2, 1, 3), (x2(0), y2(0), z2(0))=(1, 2, 2), 定理1中选取滑模面s(t)=e1+e2+e3, 控制器u(t)=(b-a)e1-(b+c)e2+me3-
| $ s\left( t \right) = {e_2}\left( t \right) + \int_0^t {\left[ {k{e_2}\left( \tau \right) + b{e_1}\left( \tau \right) - l\left( {\sin {z_2}\left( \tau \right) - \sin {z_1}\left( \tau \right)} \right)} \right]} {\rm{d}}\tau 。$ |
定理1、2中的系统误差曲线见图 2、3, 从图 2、3中可以看出, 初始时刻系统误差曲线相距甚远, 随时间推移, 系统误差渐趋一致, 另外定理1与定理2比较, 定理1中的切换面简单, 是一种线性的滑模面, 而定理2中的滑模面是一种非线性曲面, 定理2中的控制器比定理1更简单, 从而能够利用很小的控制输入实现对系统进行同步控制, 从而便于实现。另外从图 2、3取得同步的所需时间上面也能看到, 定理1中当t>0.27 s以后系统取得同步, 定理2中当t>0.20 s以后系统取得同步, 显然定理2中达到同步时间更短。
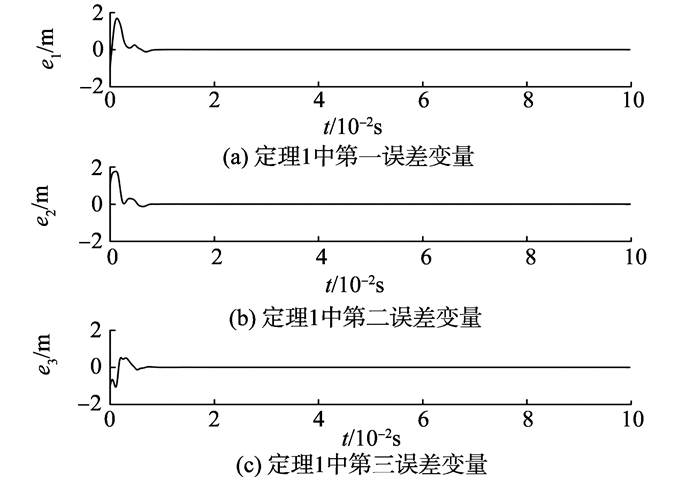
|
图 2 定理1中的系统误差曲线 Figure 2 The system errors of theorem 1 |

|
图 3 定理2中的系统误差曲线 Figure 3 The system errors of theorem 2 |
基于滑模及比例积分滑模控制方法研究纠缠混沌系统的滑模同步问题, 设计滑模面和控制器, 给出系统取得同步的两个充分性条件, 研究结果表明:一定条件下纠缠混沌系统的主从系统是滑模同步与比例积分滑模同步的, 并给出严格的数学推理和证明过程, 最后数值算例验证了该方法的可行性与有效性。
| [1] |
毛北行, 王东晓. 分数阶多涡卷系统滑模控制混沌同步[J].
山东大学学报(工学版), 2017, 47(3): 79-83 MAO Beixing, WANG Dongxiao. Sliding mode chaos synchronization control of a class of fractional-order multi-scroll systems[J]. Journal of Shandong University(Engineering Science), 2017, 47(3): 79-83 |
| [2] |
毛北行, 李巧利. 分数阶参数不确定系统的异结构混沌同步[J].
中国海洋大学学报(自然科学版), 2017, 47(7): 149-152 MAO Beixing, LI Qiaoli. Chaos synchronization betweendifferen fractional-order systems with uncertain parameters[J]. Periodical of Ocean University of China, 2017, 47(7): 149-152 |
| [3] |
毛北行, 孟晓玲. 具有死区输入的分数阶多涡卷混沌系统的有限时间同步[J].
浙江大学学报(理学版), 2017, 44(3): 302-306 MAO Beixing, MENG Xiaoling. Finite-time synchronization of fractional-order multi-scroll systems with dead-zone input[J]. Journal of Zhejiang University(Science Edition), 2017, 44(3): 302-306 |
| [4] | AHMAD W, ELKHAZALI R. Fractional-order dynamical models of love[J]. Chaos Soliton Fract, 2007, 33(4): 1367-1375 DOI:10.1016/j.chaos.2006.01.098 |
| [5] |
刘恒, 余海军, 向伟. 带有未知扰动的多涡卷混沌系统修正函数时滞投影同步[J].
物理学报, 2012, 61(18): 5031-5036 LIU Heng, YU Haijun, XIANG Wei. Modified function projective lag synchronization for multi-scroll chaotic system with unknown disturbances[J]. Acta Physica Sinica, 2012, 61(18): 5031-5036 |
| [6] |
毛北行. 两类分数阶系统的观测器同步[J].
吉林大学学报(理学版), 2017, 55(1): 139-144 MAO Beixing. Observer synchronization of two kinds of fractional-order systems[J]. Journal of Jilin university(Science Edition), 2017, 55(1): 139-144 |
| [7] | MOHAMMAD P A. Robust finite-time stabilization of fractional-order chaotic susyems based on fractional Lyapunov stability theory[J]. Journal of Computation and Nonlinear Dynamics, 2012, 32(7): 1011-1015 |
| [8] | MILAD Mohadeszadeh, HADI Delavari. Synchronization of fractional order hyper-chaotic systems based on a new adaptive sliding mode control[J]. International Journal Dynam Control, 2015, 10(7): 435-446 |
| [9] |
毛北行, 程春蕊. 分数阶Victor-Carmen混沌系统的自适应滑模控制[J].
山东大学学报(工学版), 2017, 47(4): 31-36 MAO Beixing, CHENG Chunrui. Self-adaptive sliding mode control of fractional-order Victor-Carmen chaotic systems[J]. Journal of Shandong University(Engineering Science), 2017, 47(4): 31-36 |
| [10] | BHAT S P, BERNATEIN D S. Geometric homogeneity with applications to finite-time stability[J]. Mathematics of Control Signals and Systems, 2005, 17(2): 101-127 DOI:10.1007/s00498-005-0151-x |
| [11] | MOHAMMAD P A, SOHRAB K, GHASSEM A. Finite-time synchronization of two different chaotic systems with unknown parameters via sliding mode technique[J]. Applied Mathematical Modelling, 2011, 35(6): 3080-3091 DOI:10.1016/j.apm.2010.12.020 |
| [12] |
仲启龙, 邵永辉, 郑永爱. 分数阶混沌系统的主动滑模同步[J].
动力学与控制学报, 2015, 13(1): 18-22 ZHONG Qilong, SHAO Yonghui, ZHENG Yongai. Forwardly sliding mode synchronization of the fractional order chaotic systems[J]. Journal of Dynamics and Control, 2015, 13(1): 18-22 |
| [13] |
张燕兰. 分数阶Rayleigh-Duffling-like系统的自适应追踪广义投影同步[J].
动力学与控制学报, 2014, 12(4): 348-352 ZHANG Yanlan. Adaptive tracking generalized projective synchronization of fractional Rayleigh-Duffling-like system[J]. Journal of Dynamics and Control, 2014, 12(4): 348-352 |
| [14] |
徐瑞萍, 高明美. 自适应终端滑模控制不确定混沌系统的同步[J].
控制工程, 2016, 23(5): 715-719 XU Ruiping, GAO Mingmei. Synchronization of chaotic susyems with uncertainty using adaptive terminal sliding mode controller[J]. Control Engineering of China, 2016, 23(5): 715-719 |
| [15] |
马珍珍, 肖剑, 杨叶红. 一类具有二次项的新分数阶Mavpd混沌系统[J].
武汉大学学报(工学版), 2014, 47(2): 276-285 MA Zhenzhen, XIAO Jian, YANG Yehong. A type of fractional-order chaotic systems with quadratic term[J]. Engineering Journal of Wuhan University, 2014, 47(2): 276-285 |
| [16] |
侯瑞茵, 李俨, 侯明善. 比例积分追踪制导方法研究[J].
西北工业大学学报, 2014, 32(2): 303-308 HOU Ruiyin, LI Yan, HOU Mingshan. A proportional plus integral pursuit guidance law[J]. Journal of Northwestern Polytechnical University, 2014, 32(2): 303-308 DOI:10.3969/j.issn.1000-2758.2014.02.027 |
| [17] |
徐瑞萍, 高明美, 刘振. 一个系混沌系统的滑模控制[J].
青岛大学学报(自然科学版), 2012, 25(3): 26-29 XU Ruiping, GAO Mingmei, LIU Zhen. Sliding mode control of a new chaos system[J]. Journal of Qingdao University(Natural Science Edition), 2012, 25(3): 26-29 DOI:10.3969/j.issn.1006-1037.2012.08.007 |
| [18] | ZHANG H T, LIU X Z. Chaos entanglement:a new approach to generate chaos[J]. International Journal of Bifurcation and Chaos, 2013, 23(5): 1330-1411 |
| [19] |
杨敏, 俞建宁, 张建刚, 等. 一个新构造混沌纠缠系统的动力学分析[J].
山东理工大学学报(自然科学版), 2014, 28(10): 16-23 YANG Min, YU Jianning, ZHANG Jiangang, et al. Dynamical analysis of a new chaos entanglement system[J]. Journal of Shandong University of Technology(Natural Science Edition), 2014, 28(10): 16-23 |
| [20] | 梅生伟, 申铁龙, 刘志康. 现代鲁棒控制理论与应用[M]. 北京清华大学出版社, 2003. |



