近几年, 人们常听“刷脸”一词, 如:刷脸签到、刷脸取款、刷脸开锁等, 曾经的“刷指纹”时代已被“刷脸”时代替代。其实, 无论是“刷脸”还是“刷指纹”, 都是图像识别在实际生活中的一种应用, 是从图像中提取特征, 通过分类器进行分类并进行匹配。然而, 面部识别技术却要远远复杂于指纹识别技术, 面部图像往往会受平移、旋转或光照变化的影响, 这给特征提取带来了诸多困难。
特征提取是图像分类[1-2]、识别[3-4]、语义检测[5-6]等任务的一个关键环节, 分类器的推广性能严重依赖于图像特征的质量。目前, 大多数的特征提取方法只考虑了图像的判别信息, 如主成分分析(principal component analysis, PCA)[7-8]、线性判别分析(linear discriminant analysis, LDA)[9-10]等, 并没有考虑图像在某些变换下的不变性, 尤其是在平移、旋转和光照下的不变性。也有一些方法考虑了图像在平移、旋转和光照下的不变性, 如尺度不变特征变换(scale-invariant feature transform, SIFT)[11]、方向梯度直方图(histogram of oriented gradient, HOG)[12]、invariant scattering convolution network[13]等, 但无法提取图像的判别信息。2013年, 文献[14]提出了一种将PDEs应用于计算机视觉的方法, 并已成功地用于对象检测、彩色图像转灰度以及去马赛克等任务。2015年, 文献[15]提出了一种为视觉分析设计PDEs的方法。2017年, 文献[16]提出了一种采用PDEs提取图像特征的方法, 所提方法不仅考虑了图像的判别信息, 还考虑了图像在平移和旋转下的不变性, 同时通过压缩函数的作用对光照具有鲁棒性。但不足之处是文献[16]中没有考虑PDEs的进化次数和压缩函数的压缩速度对特征质量的影响。
本研究在文献[16]的基础上, 着重研究了PDEs的进化次数和压缩函数的压缩速度对图像特征质量的影响。通过大量的试验验证: (1) PDEs本身具有降噪(遮挡)功能、对光照具有鲁棒性且可提取图像的判别信息; (2) PDEs的进化次数以及压缩函数的压缩速度与所提特征的质量密切相关。进化次数过多或压缩速度过快都将严重影响特征的质量。
1 相关工作根据偏微分方程理论, 基本微分不变量(见表 1, 本研究只使用直到二阶的基本微分不变量)的线性组合仍具有平移和旋转不变性。此外, 在基本微分不变量的基础上作用一个形如g(x)=x/(1+|x|)的压缩映射(即g(invi(u))), 仍是基本微分不变量。
| 表 1 直到二阶的基本微分不变量 Table 1 Rotational invariants up to second order |
表 1中的u是输入图像的进化特征矩阵, ▽u是u的梯度, Hu是u的Hessian阵, tr Hu表示矩阵Hu的迹。
给定c类图像数据集{(Im, hm)}m=1M ∈Rd1×d2×Rc, 其中Im是输入图像, hm是Im的标签向量, 若Im属于第i类, 则hmi=1;否则hmi=0。记H=[h1, …, hM]∈Rc×M。基于PDEs的图像特征学习模型[16]可表示为
| $ \begin{array}{l} \mathop {\min }\limits_{\mathit{\boldsymbol{W}},\left\{ {{a_i}\left( t \right)} \right\}} \frac{1}{M}\left\| {\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{W}} \cdot \mathit{\boldsymbol{U}}\left| {_{t = T}} \right.} \right\|_F^2 + \lambda \left\| \mathit{\boldsymbol{W}} \right\|_F^2\\ \;\;{\rm{s}}.{\rm{t}}.\frac{{\partial {\mathit{\boldsymbol{u}}_m}}}{{\partial t}} = \sum\limits_{i = 0}^5 {{a_i}\left( {x,y,t} \right)g\left( {{\rm{in}}{{\rm{v}}_i}\left( {{\mathit{\boldsymbol{u}}_m}\left( {x,y,t} \right)} \right)} \right)} ,\left( {x,y,t} \right) \in \mathit{\Omega } \times \left[ {0,T} \right],\\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{u}}_m}\left( {x,y,t} \right) = 0,\left( {x,y,t} \right) \in \partial \mathit{\Omega } \times \left[ {0,T} \right],\\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{u}}_m}\left| {_{t = 0}} \right.\left( {x,y,t} \right) = {\mathit{\boldsymbol{I}}_m},\left( {x,y} \right) \in \mathit{\Omega }, \end{array} $ | (1) |
其中:(x, y)∈Ω是空间变量, t∈[0, T]是时间变量, ∂Ω是Ω的边界, W=Rc×d1d2是权矩阵, U|t=T=[vec(u1|t=T), …, vec(uM|t=T)]∈Rd1d2×M, vec A表示矩阵A的向量化, {aj(x, y, t)}j=05是控制参数, g(x)=x/(1+|x|)是压缩函数。
引理1[16] 若PDEs (1)是平移不变的, 则参数{aj(x, y, t)}j=05与空间变量(x, y)无关。
引理2[16] 若F(u, x, y, t)是基本微分不变量的函数, 则u(t)通过PDEs的进化后仍保持平移旋转不变。
由引理1和引理2, 为了保持进化后的平移和旋转不变性, 模型(1)可表示为:
| $ \begin{array}{l} \mathop {\min }\limits_{\mathit{\boldsymbol{W}},\left\{ {{a_i}\left( t \right)} \right\}} \frac{1}{M}\left\| {\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{W}} \cdot \mathit{\boldsymbol{U}}\left| {_{t = T}} \right.} \right\|_F^2 + \lambda \left\| \mathit{\boldsymbol{W}} \right\|_F^2\\ \;\;{\rm{s}}.{\rm{t}}.\frac{{\partial {\mathit{\boldsymbol{u}}_m}}}{{\partial t}} = \sum\limits_{i = 0}^5 {{a_i}\left( t \right)g\left( {{\rm{in}}{{\rm{v}}_i}\left( {{\mathit{\boldsymbol{u}}_m}\left( t \right)} \right)} \right)} ,\left( {x,y,t} \right) \in \mathit{\boldsymbol{Q}},\\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{u}}_m}\left( {x,y,t} \right) = 0,\left( {x,y,t} \right) \in \mathit{\Gamma },\\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{u}}_m}\left| {_{t = 0}} \right.\left( {x,y,t} \right) = {\mathit{\boldsymbol{I}}_m},\left( {x,y} \right) \in \mathit{\Omega }, \end{array} $ | (2) |
为了便于求解, 利用差分法离散模型(2)。利用中心差分
| $ \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial x}} = \frac{{\mathit{\boldsymbol{u}}\left( {x + 1,y} \right) - \mathit{\boldsymbol{u}}\left( {x - 1,y} \right)}}{2}, $ |
| $ \frac{{{\partial ^2}\mathit{\boldsymbol{u}}}}{{\partial {x^2}}} = \mathit{\boldsymbol{u}}\left( {x + 1,y} \right) - \mathit{\boldsymbol{u}}\left( {x - 1,y} \right) - 2\mathit{\boldsymbol{u}}\left( {x,y} \right), $ |
| $ \frac{{{\partial ^2}\mathit{\boldsymbol{u}}}}{{\partial x\partial y}} = \left( {\mathit{\boldsymbol{u}}\left( {x + 1,y} \right) - \mathit{\boldsymbol{u}}\left( {x - 1,y} \right)} \right) + \left( {\mathit{\boldsymbol{u}}\left( {x,y + 1} \right) - \mathit{\boldsymbol{u}}\left( {x,y - 1} \right)} \right), $ |
离散空间导数, 利用前向差分
| $ \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} = \frac{{\mathit{\boldsymbol{u}}\left( {t + \Delta t} \right) - \mathit{\boldsymbol{u}}\left( t \right)}}{{\Delta t}}, $ |
离散时间导数。记离散的时间变量为ti=i·Δt, i=0, …, N, 其中:Δt为离散步长, N为进化次数。再记umn=um(x, y, tn), ain=ai(tn), 则模型(2)的PDEs约束可转化为进化公式
| $ \mathit{\boldsymbol{u}}_m^0 = {\mathit{\boldsymbol{I}}_m},\mathit{\boldsymbol{u}}_m^{n + 1} = \mathit{\boldsymbol{u}}_m^n + \Delta t\sum\limits_{i = 0}^5 {a_i^ng\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)} \right)} \in {{\bf{R}}^{{d_1} \times {d_2}}},\;\;\;n = 0,1, \cdots ,N - 1,m = 1, \cdots ,M。$ | (3) |
进而, 模型(2)可表示为
| $ \begin{array}{l} \mathop {\min }\limits_{\mathit{\boldsymbol{W}},\mathit{\boldsymbol{A}}} \mathit{\boldsymbol{E}}\left( {\mathit{\boldsymbol{W}},\mathit{\boldsymbol{A}}} \right) = {M^{ - 1}}\left\| {\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{U}}^N}} \right\|_F^2 + \lambda \left\| \mathit{\boldsymbol{W}} \right\|_F^2\\ {\rm{s}}.{\rm{t}}{\rm{.}}\;\mathit{\boldsymbol{u}}_m^0 = {\mathit{\boldsymbol{I}}_m},\mathit{\boldsymbol{u}}_m^{n + 1} = \mathit{\boldsymbol{u}}_m^n + \Delta t\sum\limits_{i = 0}^5 {a_i^ng\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)} \right)} \in {{\bf{R}}^{{d_1} \times {d_2}}},\;\;\;n = 0,1, \cdots ,N - 1,m = 1, \cdots ,M, \end{array} $ | (4) |
式中:A=[ain]N×6, UN=[vec(u1N, …, vec(uMN)]∈Rd1d2×M。从公式(3)和模型(4)可以看出, 分类的准确性严重依赖于N次进化后的图像特征矩阵u1N, …, uMN, 而这些特征矩阵又依赖于参数矩阵A。
关于矩阵A是如何进化的、进化次数N如何选取以及压缩函数的压缩速度对特征矩阵的影响, 文献[16]没有加以考虑。基于此, 第2节给出矩阵A的进化迭代算法, 第3节通过大量的试验讨论PDEs的进化次数N以及压缩函数的压缩速度对图像特征矩阵质量的影响。
2 矩阵A的进化迭代算法下面利用梯度下降法进化迭代矩阵A。记Un=[vec(u1n), …, vec(uMn)]∈Rd1d2×M(n=0, 1, …, N-1)由式(3)和链式法则可得
| $ \begin{array}{l} {\rm{vec}}\left( {\frac{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}}}{{\partial a_i^n}}} \right) = \frac{{\partial {\rm{vec}}\left( {\mathit{\boldsymbol{u}}_m^{n + 1}} \right)}}{{\partial a_i^n}} = \Delta t \cdot {\rm{vec}}\left( {g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)} \right)} \right) \in {{\bf{R}}^{{d_1}{d_2}}},\\ \frac{{\partial {\mathit{\boldsymbol{U}}^{n + 1}}}}{{\partial a_i^n}} = \Delta t\left[ {{\rm{vec}}\left( {g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_1^n} \right)} \right)} \right), \cdots ,{\rm{vec}}\left( {g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_M^n} \right)} \right)} \right)} \right] = \Delta t\mathit{\boldsymbol{B}}_i^n \in {{\bf{R}}^{{d_1}{d_2} \times M}},\\ \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial a_i^n}} = \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^{n + 1}}}} \cdot \frac{{\partial {\mathit{\boldsymbol{U}}^{n + 1}}}}{{\partial a_i^n}} = \left\langle {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^{n + 1}}}},\frac{{\partial {\mathit{\boldsymbol{U}}^{n + 1}}}}{{\partial a_i^n}}} \right\rangle = \Delta t{\rm{tr}}\left[ {{{\left( {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^{n + 1}}}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{B}}_i^n} \right],\\ \;\;\;i = 0, \cdots ,5,n = 0, \cdots ,N - 1, \end{array} $ | (5) |
其中Bin=[vec(g(invi(u1n))), …, vec(g(invi(uMn)))]∈Rd1d2×M。
下面计算 ∂E/∂Un∈Rd1d2×M, n=0, …, N。
当n=N时, 由于
| $ \begin{array}{l} \;\;\;\;\mathit{\boldsymbol{E}} = {M^{ - 1}}{\rm{tr}}\left( {{{\left( {\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{U}}^N}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{U}}^N}} \right)} \right) + \lambda \left\| \mathit{\boldsymbol{W}} \right\|_F^2 = \\ {M^{ - 1}}\left( {\left\| {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{U}}^N}} \right\|_F^2 - 2\left\langle {{\mathit{\boldsymbol{U}}^N},{\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{H}}} \right\rangle + \left\| \mathit{\boldsymbol{H}} \right\|_F^2} \right) + \lambda \left\| \mathit{\boldsymbol{W}} \right\|_\mathit{\boldsymbol{F}}^2, \end{array} $ |
所以
| $ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^N}}} = 2{M^{ - 1}}\left( {{\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{U}}^N} - {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{H}}} \right) = 2{M^{ - 1}}{\mathit{\boldsymbol{W}}^{\rm{T}}}\left( {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{U}}^N} - \mathit{\boldsymbol{H}}} \right) \in {{\bf{R}}^{{d_1}{d_2} \times M}}。\end{array} $ | (6) |
当n≤N-1时, 根据链式法则, 位于点(p, q)处的偏导数为:
| $ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^n}}\left( {p,q} \right) = \left( {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}}} \cdot \frac{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}}}{{\partial \mathit{\boldsymbol{u}}_m^n}}} \right)\left( {p,q} \right) = \left[ {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}}} \cdot \left( {1 + \Delta t\sum\limits_{i = 0}^5 {a_i^n\frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n}}} } \right)} \right]\left( {p,q} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}}}\left( {p,q} \right) + \Delta t\sum\limits_{i = 0}^5 {a_i^n\left[ {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}}} \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)} \right)}}{{\partial u_m^n}}} \right]} \left( {p,q} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}}}\left( {p,q} \right) + \Delta t\sum\limits_{i = 0}^5 {a_i^n\left[ {\sum\limits_r {\sum\limits_s {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}}}\left( {r,s} \right)} } \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)} \right)\left( {r,s} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n}}} \right]} \left( {p,q} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}}}\left( {p,q} \right) + \Delta t\sum\limits_{i = 0}^5 {a_i^n\left[ {\sum\limits_r {\sum\limits_s {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}\left( {r,s} \right)}}} } \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)} \right)\left( {r,s} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n\left( {p,q} \right)}}} \right]} , \end{array} $ |
其中
| $ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^n}}\left( {p,q} \right) = \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}}}\left( {p,q} \right) + \Delta t\sum\limits_{i = 0}^5 {a_i^n\left[ {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}\left( {p + 1,q} \right)}} \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)\left( {p + 1,q} \right)} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n\left( {p,q} \right)}} + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}\left( {p - 1,q} \right)}} \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)\left( {p - 1,q} \right)} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n\left( {p,q} \right)}} + \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}\left( {p,q + 1} \right)}} \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)\left( {p,q + 1} \right)} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n\left( {p,q} \right)}} + \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}\left( {p,q - 1} \right)}} \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)\left( {p,q - 1} \right)} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n\left( {p,q} \right)}} + \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}\left( {p,q} \right)}} \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)\left( {p,q} \right)} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n\left( {p,q} \right)}}} \right]。\end{array} $ |
记
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{Z}}\left( {i,m,n} \right)\left( {p,q} \right) = \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}\left( {p + 1,q} \right)}} \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)\left( {p + 1,q} \right)} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n\left( {p,q} \right)}} + \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}\left( {p - 1,q} \right)}} \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)\left( {p - 1,q} \right)} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n\left( {p,q} \right)}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}\left( {p,q + 1} \right)}} \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)\left( {p,q - 1} \right)} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n\left( {p,q} \right)}} + \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}\left( {p,q - 1} \right)}} \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)\left( {p,q - 1} \right)} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n\left( {p,q} \right)}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}\left( {p - 1,q} \right)}} \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)\left( {p - 1,q} \right)} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n\left( {p,q} \right)}} + \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{u}}_m^{n + 1}\left( {p,q} \right)}} \cdot \frac{{\partial g\left( {{\rm{in}}{{\rm{v}}_i}\left( {\mathit{\boldsymbol{u}}_m^n} \right)\left( {p,q} \right)} \right)}}{{\partial \mathit{\boldsymbol{u}}_m^n\left( {p,q} \right)}},\\ \mathit{\boldsymbol{Z}}\left( {i,m,n} \right) = \left[ {\mathit{\boldsymbol{Z}}\left( {i,m,n} \right)\left( {p,q} \right)} \right] \in {{\bf{R}}^{{d_1} \times {d_2}}}。\end{array} \right. $ |
则
再记
| $ \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^n}}} = \left[ {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\rm{vec}}\left( {\mathit{\boldsymbol{u}}_1^n} \right)}}, \cdots ,\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\rm{vec}}\left( {\mathit{\boldsymbol{u}}_M^n} \right)}}} \right] = \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^{n + 1}}}} + \Delta t\sum\limits_{i = 0}^5 {a_i^n\mathit{\boldsymbol{C}}_i^n} \in {{\bf{R}}^{{d_1}{d_2} \times M}},\;\;\;n = 0, \cdots ,N - 1。$ | (7) |
综合(6)和(7)式, 可得递推公式:
| $ \left\{ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^N}}} = 2{M^{ - 1}}\left( {{\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{U}}^N} - {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{H}}} \right) = 2{M^{ - 1}}{\mathit{\boldsymbol{W}}^{\rm{T}}}\left( {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{U}}^N} - \mathit{\boldsymbol{H}}} \right),\\ \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^{N - 1}}}} = \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^N}}} + \Delta t\sum\limits_{i = 0}^5 {a_i^{N - 1}\mathit{\boldsymbol{C}}_i^{N - 1}} = 2{M^{ - 1}}{\mathit{\boldsymbol{W}}^{\rm{T}}}\left( {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{U}}^N} - \mathit{\boldsymbol{H}}} \right) + \Delta t\sum\limits_{i = 0}^5 {a_i^{N - 1}\mathit{\boldsymbol{C}}_i^{N - 1}} ,\\ \cdots \cdots ,\\ \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^0}}} = \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^1}}} + \Delta t\sum\limits_{i = 0}^5 {a_i^0\mathit{\boldsymbol{C}}_i^0} 。\end{array} \right. $ | (8) |
综合(5)和(8)式, 可得递推公式:
| $ \left\{ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial a_i^{N - 1}}} = \Delta t\;{\rm{tr}}\left[ {{{\left( {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^N}}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{B}}_i^{N - 1}} \right] = \left( {2\Delta t{M^{ - 1}}} \right){\rm{tr}}\left[ {\left( {{{\left( {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{U}}^N} - \mathit{\boldsymbol{H}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{WB}}_i^{N - 1}} \right.} \right],\\ \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial a_i^{N - 2}}} = \Delta t\;{\rm{tr}}\left[ {{{\left( {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^{N - 1}}}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{B}}_i^{N - 2}} \right] = \Delta t\;{\rm{tr}}\left[ {{{\left( {2{M^{ - 1}}{\mathit{\boldsymbol{W}}^{\rm{T}}}\left( {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{U}}^N} - \mathit{\boldsymbol{H}}} \right) + \Delta t\sum\limits_{i = 0}^5 {a_i^{N - 1}\mathit{\boldsymbol{C}}_i^{N - 1}} } \right)}^{\rm{T}}}\mathit{\boldsymbol{B}}_i^{N - 2}} \right],\\ \cdots ,\\ \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial a_i^0}} = \Delta t\;{\rm{tr}}\left[ {{{\left( {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial {\mathit{\boldsymbol{U}}^1}}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{B}}_i^0} \right],\;\;\;\;i = 0, \cdots ,5。\end{array} \right. $ | (9) |
利用梯度下降法, 可得矩阵A的进化迭代公式:
| $ {\left( {a_i^{n + 1}} \right)^{k + 1}} = {\left( {a_i^n} \right)^k} - \eta {\left( {\frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial a_i^n}}} \right)^k},i = 0, \cdots ,5,n = 0, \cdots ,N - 1, $ | (10) |
其中η>0是步长。下面给出具体算法。
算法1 (矩阵A的进化迭代算法)
(1) 初始化。设k=0, ε>0, ρ=0.95, N=5, η=1, Δt=0.5。在[-1, 1]中均匀采样得矩阵Ak∈RN×6。
(2) 利用式(3)计算(Un)k, n=0, 1, …, N-1, 其中A=Ak。
(3) 利用模型(4)计算Wk, 其中UN=(UN)k。
(4) 计算Ek=M-1‖H-Wk(UN)k‖F2+λ‖Wk‖F2。
(5) 利用式(8), 计算
(6) 利用式(9), 计算
(7) 更新迭代步长η←ρη。
(8) 利用式(10)更新Ak至Ak+1。
(9) 利用式(3)更新(Un)k至(Un)k+1, 其中A=Ak+1。
(10)利用模型(4)计算Wk+1, 其中UN=(UN)k+1。
(11)计算Ek+1=M-1‖H-Wk+1(UN)k+1‖F2+λ‖Wk+1‖F2。
(12)若‖Ek+1-Ek‖F2<ε, 停止迭代, 置A*←Ak+1, W*←Wk+1; 否则, 置k←k+1, 转(5)。
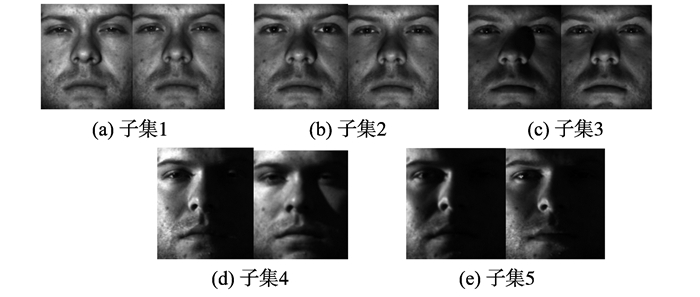
3 进化次数和压缩速度对图像特征质量的影响为了测试PDEs的进化次数和压缩函数的压缩速度对图像特征质量的影响, 本研究选用Extended YaleB数据集[17]和PIE数据集[18]进行了大量的试验。Extended YaleB数据集包含38个人在不同光照不同角度(12°, 25°, 50°, 77°, 90°)下的2 414个正面照片, 每人64张, 根据光照情况分成了5个子集。PIE数据集包含68人在13个不同姿态、43种光照条件和4种不同表情下的41 368张正面照, 每个图像尺寸为64×64。图 1显示了Extended YaleB数据集中第1人的各子集中的2个样本, 图像尺寸为48×42。
|
图 1 Extended YaleB数据集中第1人5个子集中的样本图像 Figure 1 Sample images of five subsets for the first man on Extended YaleB dataset |
为了更好地说明进化次数N对特征质量的影响, 以下试验不使用压缩函数(取g(x)=x)。
3.1.1 Extended YaleB上的试验与结果分析取Extended YaleB数据集中第2人的10个图片进行试验。试验结果见图 2, 其中第1行为原始图像, 注意观察第3, 6, 9张图片的进化结果。第2行至第11行依次是第1张图片至第10张图片的进化结果, 每行从左到右分别是N=0至N=10。从图 2中可以看出:(1)随着进化次数的增加, 图像的像素差越来越小, 且图像越来越白, 这说明通过PDEs的进化, 可以减轻光照对图像特征的影响, 同时也降低了遮挡的干扰; (2)从第3张图片的进化过程可以看出, 原始图片一片漆黑, N=3, 4, 5, 6时隐约可以看到鼻子的轮廓, 之后随着进化次数的增加, 鼻子特征越来越弱; (3)从第6张图片的进化过程可以看出, 原始图像只能看到右眼角, 随着PDEs的逐次进化, 面部特征越来越明显, N=4, 5, 6时最为清晰, 之后越来越弱; (4)从第9张图片的进化过程可以看出, 原始图像一片漆黑, 进化1~3次时可隐约看到面部特征, 进化2次特征最为清晰, 之后面部特征消失。由此可以说明PDEs的进化次数不易过多。通过观察图 2, 发现迭代次数选取4, 5, 6较为合适。

|
图 2 进化次数对特征提取的影响(Extended YaleB) Figure 2 The effect of evolution times for feature extraction (Extended YaleB) |
选取PIE数据集中第22人的10个图片进行试验。试验结果见图 3, 其中第1行为原始图片, 10张图片的光照都比较暗, 注意观察第1, 2, 3, 10张图片的进化结果。第2行至第11行依次是第1张至第10张图片的进化结果, 每行从左到右分别是N=0至N=10。

|
图 3 进化次数对特征提取的影响(PIE) Figure 3 The effect of evolution times for feature extraction (PIE) |
从图 3中可以看出:(1)图片的像素差随着进化次数的增加而逐渐变小且图片越来越白, 尤其是进化次数N=6, 7, 8, 9, 10时, 人脸特征几乎全部丢失; (2)从第1张和第3张图片的进化过程可以看出, 原始图片很难分辨出五官, 但当N=1时, 五官轮廓开始变得清晰, N=2时面部特征就变得完全清晰, N=3时特征又几乎全部消失; (3)总体说来, 进化1~2次, 图片特征最为明显; (4)第4张和第9张图片进化1~5次后人脸特征较为清晰, 而第8张图片进化1~3次人脸特征较为清晰, 当N=4时面部特征已模糊。
综上所述, PDEs的进化次数会随着数据集的不同而变化, 但总体说来, 不超过5次的进化最为合适。
3.2 压缩函数及压缩速度对特征质量的影响3.1节的试验结果表明, PDEs本身对光暗具有鲁棒性且具有压缩效果。再加入压缩函数, 等同于进行二次压缩, 其目的是加快图像特征的提取速度。本研究只比较进化至5次的结果。为了说明压缩函数和压缩速度的影响, 因此选用5个压缩速度不同的压缩函数:
| $ {g_2}\left( x \right) = \frac{x}{{1 + 1/2\left| x \right|}},{g_3}\left( x \right) = \frac{x}{{1 + \left| x \right|}},{g_4}\left( x \right) = \frac{x}{{1 + 3\left| x \right|}},{g_5}\left( x \right) = \frac{x}{{1 + 5\left| x \right|}},{g_6}\left( x \right) = \frac{x}{{1 + {6^{\left| x \right|}}}}, $ |
并与无压缩函数(g1(x)=x)进行比较。为了方便比较, 选用了Extended YaleB数据集中第1人的第55张图片和第51张图片, 以及PIE数据集中第22人的第4张图片进行试验, 3张图片的光照都比较暗。试验结果见图 4~6, 其中箭头左侧为原图, 箭头右侧第一列至第六列分别对应N=0至N=5, 第1行至第6行分别对应g1(x)至g6(x)。为了检验压缩速度的影响, 将灰度图像的像素值进行了标准化, 其中0代表白色, 1代表黑色。经计算, 从g2(x)到g6(x)的压缩速度依次增加:
| $ {g_2}\left( x \right):\left[ {0,1} \right] \to \left[ {0,\frac{2}{3}} \right] \to \left[ {0,\frac{1}{2}} \right] \to \left[ {0,\frac{2}{5}} \right] \to \cdots , $ |
| $ {g_3}\left( x \right):\left[ {0,1} \right] \to \left[ {0,\frac{1}{2}} \right] \to \left[ {0,\frac{1}{3}} \right] \to \left[ {0,\frac{1}{4}} \right] \to \cdots , $ |
| $ {g_4}\left( x \right):\left[ {0,1} \right] \to \left[ {0,\frac{1}{4}} \right] \to \left[ {0,\frac{1}{7}} \right] \to \left[ {0,\frac{1}{{10}}} \right] \to \cdots , $ |
| $ {g_5}\left( x \right):\left[ {0,1} \right] \to \left[ {0,\frac{1}{6}} \right] \to \left[ {0,\frac{1}{{11}}} \right] \to \left[ {0,\frac{1}{{16}}} \right] \to \cdots , $ |
| $ {g_6}\left( x \right):\left[ {0,1} \right] \to \left[ {0,\frac{1}{{1 + e}}} \right] \to \left[ {0,\frac{1}{{\left( {1 + {{\rm{e}}^{ - e}}} \right)\left( {1 + e} \right)}}} \right] \to \cdots 。$ |

|
图 4 Extended YaleB数据集中第1人第55张图片的试验结果 Figure 4 The experimental results on the 55th image of the first man in Extended YaleB |

|
图 5 Extended YaleB数据集中第1人第51张图片的试验结果 Figure 5 The experimental results on the 51th image of the first man in Extended YaleB |

|
图 6 PIE数据集中第22人第4张图片的试验结果 Figure 6 The experimental results on the 4th image of the 22th man in PIE |
图 4和图 5分别是Extended YaleB数据集中第1人的第55张图片和第51张图片的试验结果, 图 6是PIE数据集中第22人的第4张图片的试验结果。从图 4和图 5中可以看出:(1)不使用压缩函数或者使用压缩速度慢的压缩函数(如g2(x)), 提取的特征效果最好; (2)随着压缩速度的增加, 图像特征丢失的速度越快。从图 6中可以看出:使用压缩函数和不使用压缩函数提取的特征效果相差极小, 压缩函数几乎不发挥作用。因此, 利用PDEs进行图像特征提取时, 最好不用压缩函数或选用速度较慢的压缩函数。
4 结论本研究主要研究了PDEs的进化次数以及压缩函数和压缩速度对图像特征质量的影响。通过在Extended YaleB数据集和PIE数据集上的大量试验表明, 不超过5次的进化次数, 以及不使用压缩函数或使用速度较慢的压缩函数可以更好地提取图像的特征。这为以后研究面向图像的分类、识别、检索等问题提供了一个新的预处理方法, 尤其是对噪声(遮挡)较重、光线较暗的图像更为合适。
| [1] | GAUDIOSO M, GORGONE E, LABBE M, et al. Lagrangian relaxation for SVM feature selection[J]. Computers and Operations Research, 2017, 87: 137-145 DOI:10.1016/j.cor.2017.06.001 |
| [2] | YUAN Youli, ZHANG Min, LUO Pengfei, et al. SVM-based detection in visible light communications[J]. Optik, 2017, 151: 55-64 DOI:10.1016/j.ijleo.2017.08.089 |
| [3] | AFFONSO C, ROSSI A L, VIEIRA F H, et al. Deep learning for biological image classification[J]. Expert Systems with Applications, 2017, 85: 114-122 DOI:10.1016/j.eswa.2017.05.039 |
| [4] | YANG Meng, CHANG Heyou, LUO Weixin, et al. Fisher discrimination dictionary pair learning for image classification[J]. Neurocomputing, 2017, 269: 13-20 DOI:10.1016/j.neucom.2016.08.146 |
| [5] | LI Haojie, LIU Lijuan, SUN Fuming, et al. Multi-level feature representations for video semantic concept detection[J]. Neurocomputing, 2016, 172: 64-70 DOI:10.1016/j.neucom.2014.09.096 |
| [6] | LU Bo, WANG Guoren, YUAN Ye, et al. Semantic concept detection for video based on extreme learning machine[J]. Neurocomputing, 2013, 102: 176-183 DOI:10.1016/j.neucom.2012.02.043 |
| [7] | HUANG Sheng, YANG Dan, GE Yongxin, et al. Combined supervised information with PCA via discriminative component selection[J]. Information Processing Letters, 2015, 115: 812-816 DOI:10.1016/j.ipl.2015.06.010 |
| [8] |
崔燕, 范丽亚. 高维数据正定核与不定核的KPCA变换阵比较[J].
山东大学学报(工学版), 2011, 41(1): 17-24 CUI Yan, FAN Liya. Comparison of KPCA transformation matrices with definite and indefinite kernels for high-dimensional data[J]. Journal of Shandong university(Engineering science), 2011, 41(1): 17-24 |
| [9] | GYAMFI K S, BRUSEY J, HUNT A, et al. Linear classifier design under heteroscedasticity in linear discriminant analysis[J]. Expert Systems with Applications, 2017, 79: 44-52 DOI:10.1016/j.eswa.2017.02.039 |
| [10] |
杨静, 范丽亚. 基于模糊隶属度的加权广义不定核判别分析[J].
山东大学学报(工学版), 2012, 42(3): 31-38 YANG Jing, FAN Liya. Weighted generalize indefinite kernel discriminant analysis based on fuzzy membership[J]. Journal of Shandong university(Engineering science), 2012, 42(3): 31-38 |
| [11] | LENC L, KRAL P. Automatic face recognition system based on the SIFT features[J]. Computers and Electrical Engineering, 2015, 46: 256-272 DOI:10.1016/j.compeleceng.2015.01.014 |
| [12] | ALILOU V K, YAGHMAEE F. Non-texture image inpainting using histogram of oriented gradients[J]. Journal of Visual Communication & Image Representation, 2017, 48: 43-53 |
| [13] | BRUNA J, MALLAT S. Invariant scattering convolution networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(8): 1872-1886 DOI:10.1109/TPAMI.2012.230 |
| [14] | LIU Risheng, LIN Zhouchen, ZHANG Wei, et al. Toward designing intelligent PDEs for computer vision: an optimal control approach[J]. Image and Vision Computing, 2013, 31(1): 43-56 DOI:10.1016/j.imavis.2012.09.004 |
| [15] | LIU Risheng, ZHONG Guangyu, ZHOU Pan, et al. Learning to Diffuse: A new perspective to design PDEs for visual analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(12): 2457-2471 DOI:10.1109/TPAMI.2016.2522415 |
| [16] | FANG Cong, ZHAO Zhenyu, ZHOU Pan, et al. Feature learning via partial differential equation with applications to face recognition[J]. Pattern Recognition, 2017, 69: 14-25 DOI:10.1016/j.patcog.2017.03.034 |
| [17] | GEORGHIADES A, BELHUMEUR P, KRIEGMAN D. From few to many: illuminationcone models for face recognition under variable lighting and pose[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(6): 643-660 DOI:10.1109/34.927464 |
| [18] | SAUL L K, WEINBERGER K Q, HAM J H, et al. Spectral methods for dimensionality reduction[J]. Semisupervised Learning, 2006: 293-308 |




