2. 山东电力工程咨询院有限公司, 山东 济南 250013
2. Shandong Electric Power Engineering Consulting Institute, Ltd., Jinan 250013, Shandong, China
在直流特高压输电工程中, 接地极引线发挥重要作用, 在单极大地运行方式下, 它将直流电流引入大地, 把大地作为廉价和低损耗回路。在工程具体实施过程中, 为节省输电线路对土地资源的占用, 在换流站附近, 往往因地制宜的使接地极引线线路与直流输电线路同塔共架。与常规分别单独架设的直流输电线路和接地极引线线路相比, 共塔段的杆塔更高, 杆塔遭受雷击的概率明显提高。从输电线路绝缘配合与防雷接地的角度来看, 同塔共架段线路的主要特点如下:
(1) 接地极引线招弧角间隙面临更为频繁的雷电过电压冲击。接地极线路正常运行时引线电压很低, 一般不足10 kV, 绝缘要求很容易满足[1]。威胁接地极线路绝缘安全的主要因素是来自雷击后的续流, 也就是雷电引发招弧角间隙放电, 且在接地极线路直流续流的作用下, 可能建立稳定的电弧, 导致接地故障发生[2-3]。
(2) 直流输电线路反击耐雷水平明显提升。类似于同塔混压线路中低电压等级线路对高电压等级线路形成差绝缘保护, 使高电压等级线路难以发生闪络。接地极线路的存在, 对其上方直流线路的反击耐雷水平也会产生影响。
为定量分析上述特征, 建立符合实际的仿真模型是非常有必要的。文献[4]开展招弧角的燃弧试验, 研究电压等级±800 kV、输送容量5 000 MW某特高压直流线路接地极线路的绝缘配合, 分析电弧拉伸效应和接地极线路参数对招弧角保护性能的影响。文献[5]总结开放空间电弧研究的现状, 文献[6]分析天广直流、兴安直流接地极线路招弧角的运行情况。目前的研究主要集中在常规接地极线路招弧角运行情况分析、防雷性能及绝缘配合优化等领域, 对同塔共架的相关研究较为缺乏。
电弧的仿真模型常用于输电线路单相接地故障分析, 为减小潜供电流、优化整定重合闸时间及完善保护策略等提供计算依据[7], 但电弧模型在招弧角间隙仿真应用方面的研究较为缺乏。为验证模型对本研究的适用性, 首先利用ATP-EMTP建立文献[4]试验用的电路仿真模型, 然后对试验数据与仿真结果进行对比分析。随后建立具有频率特性的输电线路模型, 仿真研究共塔段杆塔遭受雷击后的响应。
1 招弧角电弧模型及试验验证 1.1 招弧角的放电过程招弧角由击穿放电到建立电弧可分为以下两个阶段。
第一阶段:雷电过电压使招弧角间隙击穿。仿真时, 招弧角放电采用压控开关模型。招弧角间隙取40 cm时, 其50%雷电冲击放电电压U50%=213 kV[4]。
第二阶段:充足的续流电流流过放电间隙, 建立持续的电弧。
1.2 改进的Mayr模型的数学表达及试验验证目前常用的电弧仿真模型有压控开关模型、Cassie模型、Mayr模型、Schwarz模型及控制论模型等。压控开关模型用简单的压控开关代替电弧, 对本研究来说过于简化, 无法模拟电弧的非线性电阻。Cassie电弧模型适用于小电阻大电流的电弧仿真。Mayr、Schwarz和控制论3种模型大同小异, 数学模型相对简单, 非常适合小电流电弧的仿真。由于Mayr模型能直接设置弧长, 直观反映招弧角间隙的电弧长度, 本研究采用Mayr电弧模型[1]。
根据能量平衡的原理, 经典Mayr电弧模型可演绎为[7]
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}g}}{{{\rm{d}}t}} = \frac{1}{T}\left( {G - g} \right)\\ T = \frac{{\alpha I}}{L}\\ G = \frac{{\left| i \right|}}{{VL}} \end{array} \right., $ | (1) |
式中:G为稳态电弧电导, S; g为电弧瞬时电导, S; T为电弧时间常数, s; I为电弧伏安特性曲线中的峰值电流, A, 可近似采用直接短路时的短路电流; L为电弧长度, m, 文献[8]认为电弧长度可近似为常数, L取间隙长度; α为常数, 一般取2.85×10-5; i为电弧瞬时电流, A; V为单位长度的静态电弧压降, 电弧压降V=15 kV/cm; 电弧电阻初始值取100 MΩ[7-9]。
在进行ATP-EMTP仿真时, 首先使仿真电路短路得到电流I, 然后把I代入式(1)计算T, 此后在每一个时步计算时修正动态电阻, 并以控制时变电阻的形式送入仿真电路中, 并采用欧拉法求解微分方程[9]
| $ g\left( {t + Vt} \right) = \frac{{Vt}}{T}\left( {G - g\left( t \right)} \right) + g\left( t \right)。$ | (2) |
为使数值计算更加稳定, 利用exp(x)展开为泰勒级数
| $ \exp \left( x \right) = 1 + x + \frac{{{x^2}}}{{2!}} + \frac{{{x^3}}}{{3!}} + \cdots , $ | (3) |
取展开式前两项把式(2)变形为
| $ g\left( {t + Vt} \right) = g\left( t \right) + \left[ {G - g\left( t \right)} \right] \cdot \left( {1 - \exp \left( { - \frac{{Vt}}{T}} \right)} \right)。$ | (4) |
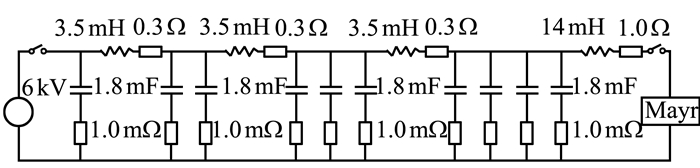
利用ATP-EMTP建立方波电流发生器及电弧放电模型, 仿真模型及元件参数见图 1。仿真模型元件参数均与文献[4]相同, 其中招弧角间隙长度为40 cm。
|
图 1 采用ATP-EMTP建立的仿真验证模型 Figure 1 Simulation verification model based on ATP-EMTP |
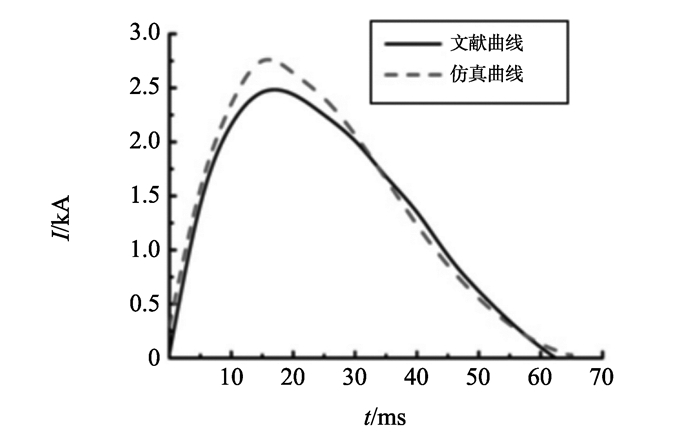
根据仿真数据与文献[4]试验数据绘制招弧角间隙的电弧电流曲线, 详见图 2。
|
图 2 仿真曲线与文献曲线对比 Figure 2 Comparison of simulation curve and document curve |
由图 2可见, 波峰段仿真电流比试验数据增大8.7%, 其余段两者基本吻合, 电流波脉宽也十分接近, 出现这种现象的原因:
(1) 在初始燃烧阶段, 电弧形态相对稳定, 电弧长度约等于间隙长度; 在电弧熄灭阶段, 方波电流发生器输出的电流逐渐减小, 电弧电阻显著增加, 电弧长度的影响愈发微弱。因此在上升和下降阶段, 两条曲线基本吻合。
(2) 在持续燃烧阶段, 电弧电流逐步达到最大值, 电弧电磁力的影响加强, 试验电弧变长。仿真模型的电弧长度仍然为间隙长度, 致使仿真电弧的电阻小于试验电弧, 仿真电流大于文献[4]电流。
尽管仿真计算和试验实测值存在一定偏差, 但本研究重点为雷电冲击时招弧角是否建弧, 而建弧阶段两条曲线吻合程度很高, 因此Mayr电弧仿真模型适用于本研究。
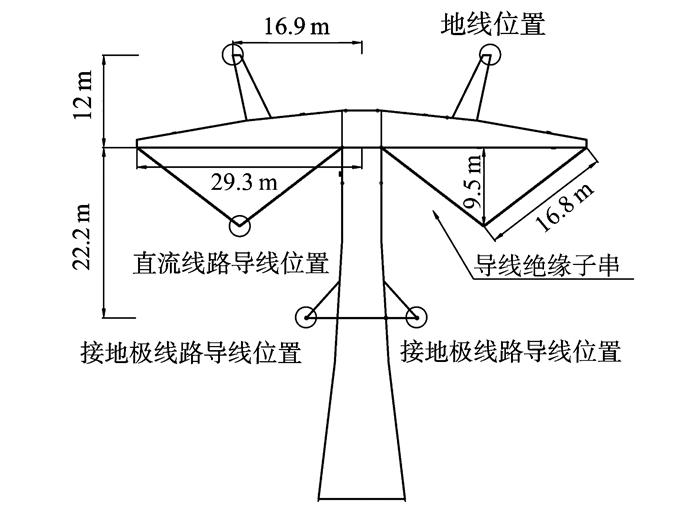
2 同塔共架线路仿真模型的建立 2.1 计算条件本研究以±1 100 kV直流线路与接地极线路共塔为例, 直流线路额定电压±1 110 kV, 额定电流5 455 A, 接地极线路全长80 km, 其中共塔段40 km, 接地极线路单独架设段40 km, 雷击发生在共塔段中部, 工频接地电阻取500 Ω, 直流线路导线采用8分裂JL1/G3A-1250/70, 接地极线路采用2分裂JLRX1/F1B-500/65碳纤维复合芯导线, 输电线路铁塔尺寸见图 3。
|
图 3 塔头示意图 Figure 3 Schematic diagram of tower head |
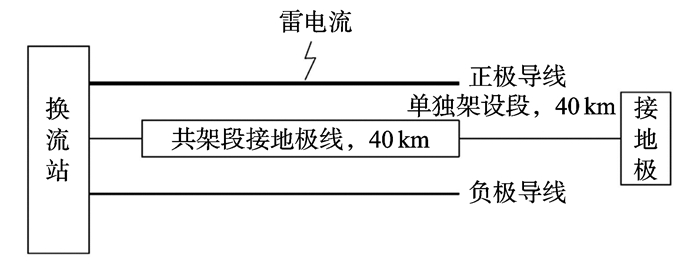
接地极线路输送电流取决于系统运行方式, 在单极大地运行方式下, 入地电流为系统的额定电流, 取5 455 A。接地极线路导线布置在杆塔两侧, 流过每侧导线的电流为总入地电流的一半[1]。接地极线路单根导线电阻0.046 67 Ω/km, 接地极接地电阻0.25 Ω。为便于研究, 规定雷击点发生在T0塔, 远离T0方向的塔号分别记为B1(F1)、B2(F2)至Bn(Fn), 接地极线路示意图见图 4。
|
图 4 接地极线路示意图 Figure 4 Schematic diagram of grounding electrode line system |
输电线路采用具有频率特性的模型[10-12], 同塔共架段采用6相电线, 接地极线路单独架设段采用3相电线。雷电流采用负极性双指数波雷电流模型[13]
| $ I = {I_m}\left( {\exp \left( { - \alpha t} \right) - \exp \left( { - \beta t} \right)} \right), $ | (5) |
式中:Im为雷电类幅值, A; α、β分别为波头、波尾时间, s。
IEEE推荐了1.2/50 μs为标准雷电过电压的波形。从各国所测得雷电流波形来看, 基本上相差不大, 波长大致在40 s左右, 波头长度大致在1~4 μs左右。根据我国的实际测量数据, 在输电线路的防雷保护设计中, 雷电流的波头长度一般取2.6 μs。本研究α取2.6 μs, β取50 μs, 考虑雷电通道波阻抗Z0的影响, 直击杆塔时, Z0取300 Ω[14]。
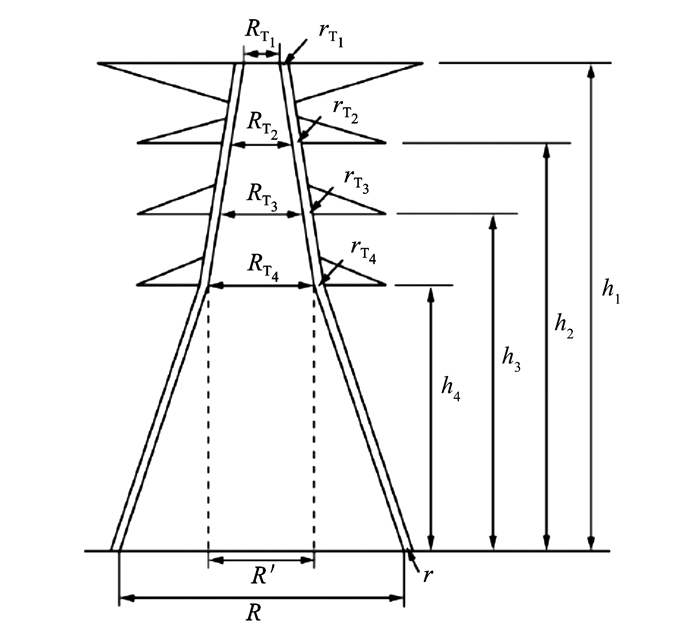
由于共塔段线路杆塔较高, 用传统的集中参数模型计算杆塔的波阻抗, 并用来评估线路的耐雷性能将带来较大的误差。采用IEEE推荐的方法, 把杆塔构件细分为横担、主材、辅材, 见图 5。并根据杆塔的实际几何尺寸计算其波阻抗[15-17]。
|
图 5 杆塔组件尺寸参数 Figure 5 Size parameters of tower components |
主材部分波阻抗按下式计算。
| $ {Z_{{{\rm{T}}_k}}} = 60\left( {\ln \frac{{2\sqrt 2 {h_k}}}{{{r_{ek}}}} - 2} \right),k = 1,2,3, $ | (6) |
其中: rek=21/8(rTk1/3r2/3)1/4(RTk1/3R2/3)3/4, 式中hk、rTk、RTk, r和R分别为图 5所示的相应部分的宽度, m。
实际测量得到增加了杆塔辅材后多导体系统的波阻抗减少10%左右, 那么辅材的波阻抗
| $ {Z_{{{\rm{L}}_k}}} = 9{Z_{{{\rm{T}}_k}}}, $ | (7) |
横担部分的波阻抗
| $ {Z_{{{\rm{A}}_k}}} = 60\left( {\ln \frac{{2{h_k}}}{{{r_{{{\rm{A}}_k}}}}}} \right), $ | (8) |
式中:hk为第k部分横担的对地高度, m; rAk为第k部分横担的等值半径, m, 可取杆塔与塔身联结处横担宽度的0.25倍。
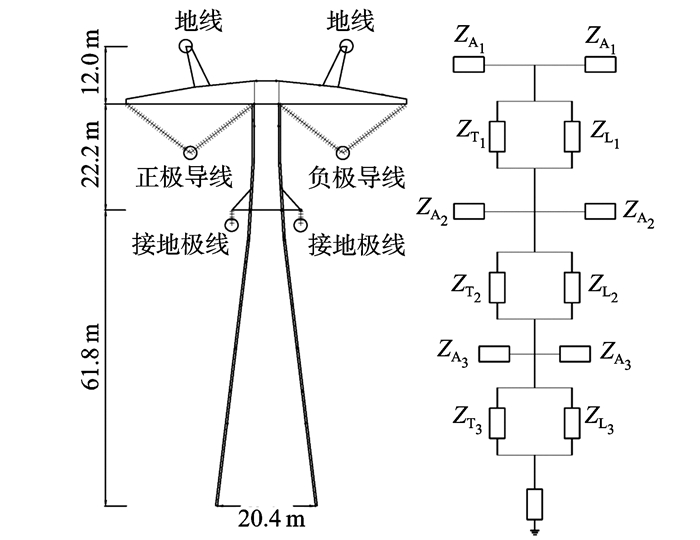
根据共塔段杆塔组件尺寸, 分别计算各段的波阻抗, 见图 6及表 1。
|
图 6 杆塔多波阻抗模型 Figure 6 Muti-wave-impendance model of tower |
| 表 1 杆塔波阻抗取值 Table 1 Wave-impendance of tower |
塔头空气间隙约9.5 m, 是典型的长空气间隙, 先导发展是长空气间隙的特有现象, 本研究采用国际大电网组织(CIGRE)推荐的先导模型进行仿真。
先导发展法的核心思想是:当线路绝缘子上电压出现的时间达到流注发展时间ts时, 先导开始发展, 其速度随施加的瞬时电压与剩余间隙长度而变。当流注占满整个间隙长度时, 间隙即闪络。当先导发生过程中施加电压下降, 先导未达到部分的平均电场降到E0以下时, 判断先导发展终止[11-13]。
| $ \left\{ \begin{array}{l} \frac{1}{{{t_{\rm{s}}}}} = 1.25 \times \frac{E}{{{E_0}}} - 0.95,\\ \frac{{{\rm{d}}L}}{{{\rm{d}}t}} = k \cdot u\left( t \right) \cdot \left[ {\frac{{u\left( t \right)}}{{d - L}} - {E_0}} \right] \end{array} \right., $ | (9) |
式中:ts为先导开始时间, us; E为最大有效场强, kV/m; E0为试验获取的最小击穿场强, kV/m; L为先导发展的长度, m; u(t)为间隙上的电压, kV; d为空气间隙长度, m; k为常数。
本研究采用负极性雷电流, 雷电击中杆塔时, 流入杆塔的电流为负极性, 导线相对于塔顶为正极性, 因此U50%取绝缘子串或空气间隙的正极性50%冲击电压。根据国际大电网组织(CIGRE)的推荐, 雷击杆塔时参数取值为[10-13]:对于空气间隙, E0取600, k取0.8, 对于盘形绝缘子串, E0取520, k取1.2。
2.4 冲击接地电阻模型由于雷电流幅值大、波形变化快, 因此需充分考虑接地电阻暂态特性和大电流冲击特性的影响。大电流流入接地电极使电极周围土壤电离, 接地电阻低于工频值, 且接地电阻越高, 降低效应表现越明显, 利用国际电工委员会(IEC)推荐的公式计算[18-19]。
| $ \left\{ \begin{array}{l} R = \frac{{{R_0}}}{{\sqrt {1 + \frac{I}{{{I_g}}}} }}\\ {I_g} = \frac{{2{\rm{ \mathsf{ π} }}{r^2}}}{\rho }{E_c}\\ {R_0} = \frac{\rho }{{2{\rm{ \mathsf{ π} }}r}} \end{array} \right., $ | (10) |
式中:I为流过塔脚电阻的雷电流, A; Ig为对应土壤电离梯度Ec的临界电流, A; R0为工频接地电阻, Ω; ρ为土壤电阻率, Ω·m。
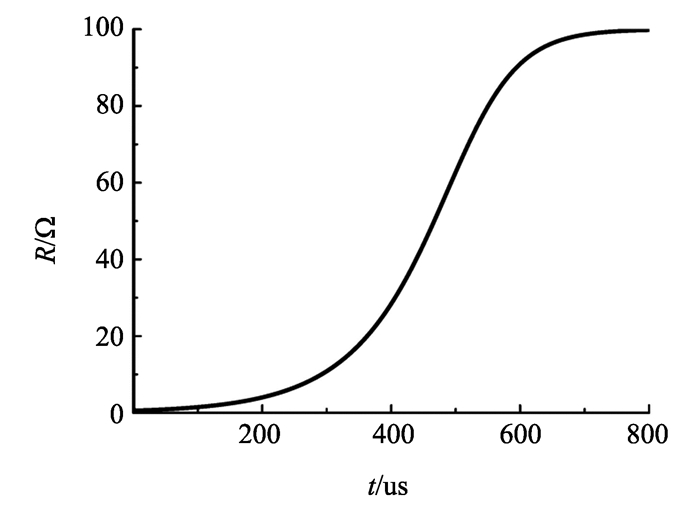
以工频接地电阻100 Ω, 土壤电阻率500 Ωm, 100 kA雷电流击中杆塔为例, 冲击接地电阻的变化见图 7。
|
图 7 冲击接地电阻随时间的变化曲线 Figure 7 Curve of the impact grounding resistance with time |
由图 7可见, 在入地雷电流的冲击下, 接地电阻迅速降低, 随着雷电波过程逐步趋向结束, 接地电阻也逐步上升至工频值。
3 仿真模型在实际工程中的应用在输电线路实际运行中, 由于接地极线路绝缘配置较为薄弱, 雷击产生的过电压很容易使接地极线路招弧角间隙击穿[13], 本研究以雷击杆塔为例进行仿真研究。
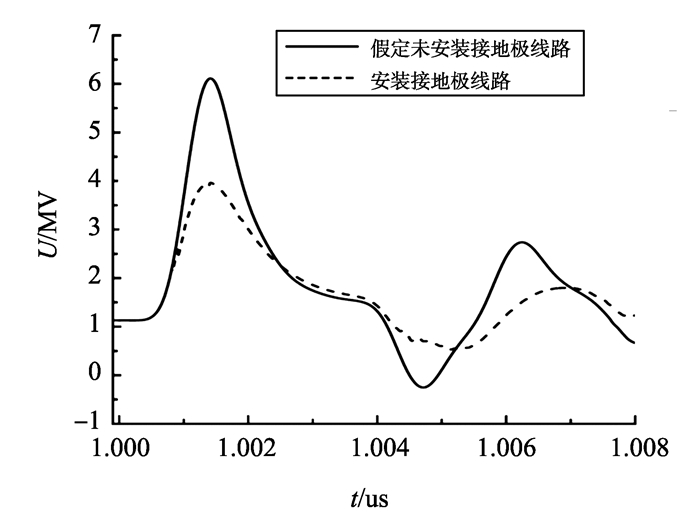
3.1 接地极线路对直流线路反击耐雷水平的影响雷击杆塔时, 雷击点附近多基杆塔的招弧角间隙击穿, 这样接地极线路起到两根类似耦合地线的作用, 一方面增加避雷线与直流导线间的耦合作用, 降低空气间隙及绝缘子串承受的冲击电压, 另一方面通过招弧角放电使雷电流分流[20], 降低杆塔电位。为研究接地极线路对直流线路反击耐雷水平的影响, 本研究分别以幅值为100 kA和210 kA的雷电流击中杆塔, 导线与杆塔间的空气间隙承受的过电压波形见图 8、9。
|
图 8 100 kA雷电流击中杆塔, 空气间隙承受的过电压 Figure 8 Overvoltage on air gap caused by 100 kA lightning current |
|
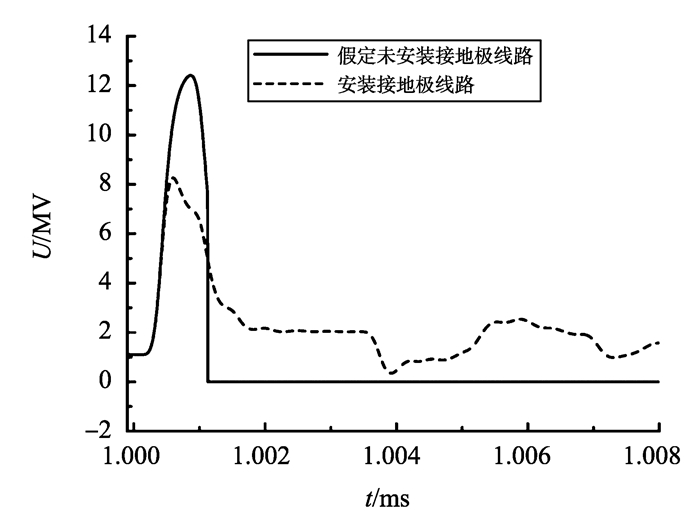
图 9 210 kA雷电流击中杆塔, 空气间隙承受的过电压 Figure 9 Overvoltage on air gap caused by 210 kAlightning current |
绝缘子串两端承受的过电压, 为横担电位与导线耦合电位、感应电位之差。波形总体上可以认为是双指数波叠加阻尼振荡, 曲线在振荡中逐渐衰减, 最后趋向于零。波形的双指数成分是由雷电流波形确定的, 而振荡是因为雷电流通道波阻抗与杆塔波阻抗不同, 电磁波多次折反射形成的。
由图 8可知, 在t=1 ms时刻, 100 kA雷电流击中杆塔, 安装接地极线路可使过电压由6.235 MV降低至3.890 MV, 降幅达2.345 MV。由图 9可知, 在t=1 ms时刻, 210 kA雷电流击中杆塔, 在假定未安装接地极线路的情况下, 空气间隙承受的电压幅值为12.5 MV, 且经过约1.1 μs的先导发展, 空气间隙击穿。在安装接地极线路的情况下, 空气间隙承受的电压幅值降低至8.1 MV, 空气间隙未被击穿。
经计算, 在不安装接地极线路的情况下, 直流线路反击耐雷水平为207 kA, 在架设接地极线路的情况下, 直流线路的反击耐雷水平提高到302 kA。结果表明, 接地极线路使直流线路的反击耐雷水平提高45.9%。
3.2 杆塔遭受雷击后的招弧角放电由于雷击产生的过电压很容易使接地极线路招弧角间隙击穿, 且高幅值雷电流出现的概率较低。本研究取具有一定代表意义的出现概率为50%的雷电流进行研究。我国一般地区雷击输电线路杆塔雷电流幅值概率分布
| $ {P_{\left( {{I_0} \ge {i_0}} \right)}} = {10^{ - \frac{{{i_0}}}{{88}}}}。$ | (11) |
经计算出现概率为50%的雷电流幅值为26 kA。雷电击中T0塔, 大部分雷电流从杆塔流入大地, 少部分雷电流沿地线向两侧传播, 每经过1基杆塔, 沿地线继续行进的雷电流幅值显著减小, 在招弧角两端产生的过电压幅值也逐步降低。幅值为26 kA的雷电流击中T0塔顶后, B5~T0塔招弧角承受的电压见图 10。

|
图 10 26 kA雷电流击中杆塔, 招弧角承受的过电压 Figure 10 Overvoltage on arcing horns caused by26 kA lightning current |
由图 10可知: T0、B1、B2、B3的招弧角两端电压超过雷电冲击的U50%=287 kV(间隙为60 cm)[4]。实际上招弧角放电后使接地极线路具有一定分流作用, 进一步降低其下一基杆塔的招弧角过电压幅值。经仿真, 雷击点T0及其附近B2、B1、T0、F1、F2共计5基塔的招弧角间隙被击穿, 而最终能否建立持续电弧, 还要看招弧角间隙长度和接地极线路的续流电流的大小。
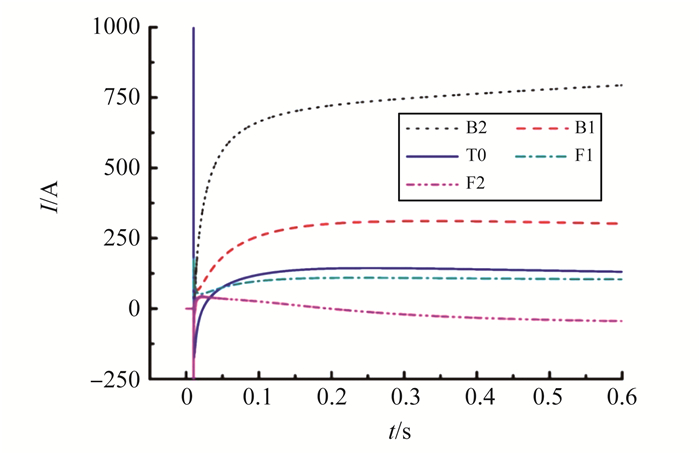
3.3 单极大地运行方式下招弧角建弧情况仿真在单极大地运行方式下, 流过每侧接地极线路的电流高达2 727.5 A, 这有助于放电的招弧角间隙建立持续的电弧, 雷击点附近招弧角击穿及建弧情况见图 11。
|
图 11 26 kA雷击杆塔引发的招弧角放电 Figure 11 Arcing horns discharge caused by 26 kAlightning current hit tower |
由图 11可知:自换流站至接地极的方向(B2塔至F2塔), 流过招弧角电弧的电流逐渐减小, 除F2塔续流电流过小不足以建立电弧外, 其余各塔均建立较为持续的电弧。经仿真, 在共塔段的末端, 接地极线路上流过的电流减小为1 362 A, 这说明共计1 365 A的电流经招弧角电弧流入大地。
4 结论本研究利用ATP-EMTP建立模型, 分析改进的Mayr电弧模型对本研究的适用性, 随后建立直流线路与接地极线路共塔共架线路的仿真模型, 分析杆塔遭受雷击后的直流线路耐雷水平和接地极线路招弧角放电情况, 主要结论如下:
(1) 雷击杆塔时, 由于接地极线路起到的差绝缘保护作用, 使直流线路的反击耐雷水平提高约45.9%。
(2) 单极大地运行情况下, 雷击点附近多基杆塔的招弧角间隙建立持续电弧, 引起接地极线路多点接地故障。
(3) 研究成果可为共塔段的直流线路防雷防护和接地极线路的故障保护设计提供理论依据。
| [1] | 赵婉君. 高压直流输电工程技术[M]. 北京: 中国电力出版社, 2011. |
| [2] |
王敩青, 杨跃光, 苏国磊, 等. 直流运行方式对接地极线路耐雷性能影响分析[J].
电瓷避雷器, 2015(4): 82-86 WANG Xiaoqing, YANG Yueguang, SU Guolei, et al. Analysis on influence of different operation mode of HVDC system on the lightning protection performance of grounding electrode line[J]. Insulators and Surge Arresters, 2015(4): 82-86 |
| [3] |
刘更生, 郑扬亮, 冉学彬. 天广直流马窝侧接地极线路招弧角运行分析[J].
电网技术, 2007, 31(Suppl.2): 37-39 LIU Gengsheng, ZHENG Yangliang, RAN Xuebin. Analysis on operational experience of grounding electrode line of mawo side in Tian-Guang HVDC transmission line with arcing horn[J]. Power System Technology, 2007, 31(Suppl.2): 37-39 |
| [4] |
李健, 李显东, 李化, 等. 特高压直流接地极线路招弧角绝缘配合试验研究[J].
高电压技术, 2016, 42(11): 3481-3487 LI Jian, LI Xiandong, LI Hua, et al. Experimental research on insulation coordination of arcing horns on UHVDC earthing lines[J]. High Voltage Engineering, 2016, 42(11): 3481-3487 |
| [5] |
张冯硕, 李健, 吴高波, 等. 直流接地极招弧角熄弧特性研究[J].
高压电器, 2016(3): 105-110 ZHANG Fengshuo, LI Jian, WU Gaobo, et al. Study on arc-extinguishing characteristics of arcing horns on DC grounding line[J]. High Voltage Apparatus, 2016(3): 105-110 |
| [6] |
郑扬亮, 冉学彬, 刘更生. 直流输电接地极线路招弧角有关问题的分析[J].
高电压技术, 2008, 34(7): 1513-1516 ZHENG Yangliang, RAN Xuebin, LIU Gengsheng. Analysis on the problems of arcing horn on grounding electrode line of HVDC system[J]. High Voltage Engineering, 2008, 34(7): 1513-1516 |
| [7] |
颜湘莲, 陈维江, 李志兵, 等. 输电线路潜供电弧自熄特性仿真[J].
高电压技术, 2012, 38(10): 2735-2741 YAN Xianglian, CHEN Weijiang, LI Zhibing, et al. Simulation for self-extinction behavior of secondary arc in transmission lines[J]. High Voltage Technology, 2012, 38(10): 2735-2741 |
| [8] | JOHNS A T, AGGARWAL R K, SONG Y H. Improved techniques for modelling fault arcs an faulted EHV transmission systems[J]. Iee Proceedings Generation Transmission & Distribution, 1994, 141(2): 148-154 |
| [9] | 李云阁. 电力系统电磁暂态计算与EMTP应用[M]. 北京: 中国水利水电出版社, 2012. |
| [10] |
叶会生, 何俊佳, 李化, 等. 雷击高压直流线路杆塔时的过电压和闪络仿真研究[J].
电网技术, 2005, 29(21): 35-39 YE Huisheng, HE Junjia, LI Hua, et al. Simulation of overvoltage and flashover caused by lightning stroke at towers of HVDC transmission line[J]. Power System Technology, 2005, 29(21): 35-39 |
| [11] | TANIGUCHI S, TSUBOI T, OKABE S, et al. Method of calculating the lightning outage rate of large-sized transmission lines[J]. IEEE Transactions on Dielectrics & Electrical Insulation, 2010, 17(4): 1276-1283 |
| [12] | YONGXIA H, LICHENG L. Influence of modeling methods on the calculated lightning surge overvoltages at a UHVDC converter station due to backflashover[J]. IEEE Transactions on Power Delivery, 2012, 27(3): 1090-1095 DOI:10.1109/TPWRD.2012.2190306 |
| [13] | TANIGUCHI S, OKABE S, ASKAWA A, et al. Flashover characteristics of long air gaps with negative switching impulses[J]. Dielectrics & Electrical Insulation IEEE Transactions on, 2008, 15(2): 399-406 |
| [14] | 中华人民共和国住房和城乡建设部. 交流电气装置的过电压保护和绝缘配合设计规范: GB/T 50064—1997[S]. 北京: 中国计划出版社, 2014. |
| [15] |
陈水明, 谢海滨, 屠幼萍, 等. ±500 kV直流极线与接地极线同塔架设时的感应过电压[J].
高电压技术, 2012, 38(5): 1186-1191 CHEN Shuiming, XIE Haibin, TU Youping, et al. Induced overvoltage while ±500kV pole line and neutral line using common-towe[J]. High Voltage Engineering, 2012, 38(5): 1186-1191 |
| [16] |
范冕, 万磊, 戴敏, 等. 不同串型设计条件下的特高压交流同塔双回线路雷电性能[J].
高电压技术, 2014, 40(12): 3902-3910 FAN Mian, WAN Lei, DAI Min, et al. Lightning performance of UHVAC double-circuit transmission lines on the same tower under different design conditions of insulator string[J]. High Voltage Engineering, 2014, 40(12): 3902-3910 |
| [17] |
王东举, 周浩, 陈稼苗, 等. 特高杆塔的多波阻抗模型设计及雷击暂态特性分析[J].
电网技术, 2007, 31(23): 11-16 WANG Dongju, ZHOU Hao, CHEN Jiamiao, et al. Design of multi-surge impedance model for ultra-high transmission tower and analysis on its transient characteristic caused by lightning stroke[J]. Power System Technology, 2007, 31(23): 11-16 |
| [18] |
张婷, 洪心, 冉洪伟, 等. 空气间隙放电对于直流输电线路耐雷性能的影响[J].
中国电力, 2016, 49(6): 107-111 ZHANG Ting, HONG Xin, RAN Hongwei, et al. Research on influence of air gap discharge on HVDC lines lightning performance[J]. Electric Power, 2016, 49(6): 107-111 |
| [19] | SHU Y B, YI H U. Research and application of the key technologies of UHV AC transmission line[J]. Proceedings of the Csee, 2007, 27(36): 1-7 |
| [20] |
葛罗, 文习山. 雷电绕击下线路避雷器的仿真计算研究[J].
电瓷避雷器, 2015, 138(3): 105-109 GE Luo, WEN Xishan. Simulation study of line arrester under lightning shielding failure[J]. Insulators and Surge Arresters, 2015, 138(3): 105-109 |




