2. 东北林业大学数学系,黑龙江 哈尔滨 150001
2. Department of Mathematics, Northeast Forestry University, Harbin 150001, Heilongjiang, China
图像增强是有目的性地突出和加强原图像中的目标区域,抑制不感兴趣的特征,增强图像的辨识度和改善图像的视觉效果。图像增强允许增强后的图像与原图不一致,其最终目的是有利于图像的进一步分析和处理。
林火遥感图像经常会由于自然因素以及设备原因造成采集到的图像对比度过低,影响进一步对图像处理的效果。为了提高林火遥感图像的清晰度并突出火场区域的边缘信息,本研究提出一种具有时滞的六维前馈神经网络模型来达到图像增强的目的。这种算法借助动力学性质,能达到很好的信号放大效果,因此,图像增强效果明显,可以起到提高图像清晰度和对比度的作用。
1 前馈神经网络模型的动力系统性质分析基于文献[1]和[2]的开创性研究工作,神经网络的理论和应用得到了广泛推广。由于神经元之间的信号交换和传输的速度限制,时间滞后在神经网络中是不可避免的。因此,时间延迟的问题在数学模型中被提出来并被受到重视。在这些模型中,不同类型的动力学行为,包括稳定性、混沌、分支(Hopf分支、全局Hopf分支、Pitchfork-Hopf分支和Hopf-Zero分支)等问题得到了深入研究[3-6]。
2004年,文献[7]首先提出一种带有离散时滞和分布时滞的二维神经网络模型
| $ \left\{ \begin{array}{l} {{\dot x}_1} = - \mu {x_1}\left( t \right) + {a_{11}}{f_{11}}\left( {\int_{ - \infty }^t {F\left( {t - s} \right){x_1}\left( {s - \tau } \right){\rm{d}}s} } \right) + {a_{12}}{f_{12}}\left( {{x_2}\left( {t - \tau } \right)} \right)\\ {{\dot x}_2} = - \mu {x_2}\left( t \right) + {a_{22}}{f_{22}}\left( {\int_{ - \infty }^t {F\left( {t - s} \right){x_2}\left( {s - \tau } \right){\rm{d}}s} } \right) + {a_{21}}{f_{21}}\left( {{x_1}\left( {t - \tau } \right)} \right) \end{array} \right., $ |
式中μ为耦合系数。如果在网络中的两个神经元对于相同的输出表现出相同的线性行为,则此方程可以改写为一个带有时滞的四维神经网络模型[8]
| $ \left\{ \begin{array}{l} {{\dot x}_1} = - {x_1}\left( t \right) + af\left( {{x_2}\left( t \right)} \right) + bf\left( {{x_3}\left( {t - \tau } \right)} \right)\\ {{\dot x}_2} = - \gamma {x_2}\left( t \right) + {x_1}\left( {t - \tau } \right)\\ {{\dot x}_3} = - {x_3}\left( t \right) + af\left( {{x_4}\left( t \right)} \right) + bf\left( {{x_1}\left( {t - \tau } \right)} \right)\\ {{\dot x}_4} = - \gamma {x_4}\left( t \right) + {x_3}\left( {t - \tau } \right) \end{array} \right.。$ |
本研究构建出一个具有时滞六维前馈神经网络模型
| $ \left\{ \begin{array}{l} {{\dot x}_1} = - {x_1}\left( t \right) + af\left( {{x_2}\left( t \right)} \right) + bf\left( {{x_1}\left( {t - \tau } \right)} \right)\\ {{\dot x}_2} = - \gamma {x_2}\left( t \right) + {x_1}\left( {t - \tau } \right)\\ {{\dot x}_3} = - {x_3}\left( t \right) + af\left( {{x_4}\left( t \right)} \right) + bf\left( {{x_1}\left( {t - \tau } \right)} \right)\\ {{\dot x}_4} = - \gamma {x_4}\left( t \right) + {x_3}\left( {t - \tau } \right)\\ {{\dot x}_5} = - {x_5}\left( t \right) + af\left( {{x_6}\left( t \right)} \right) + bf\left( {{x_3}\left( {t - \tau } \right)} \right)\\ {{\dot x}_6} = - \gamma {x_6}\left( t \right) + {x_5}\left( {t - \tau } \right) \end{array} \right., $ |
式中:γ、a和b为耦合系数; τ为时滞,τ≥0。假设输出函数为双曲正切函数f(x)=tanh x;变量xi(i=1, 2, …, 6)分别表示神经元的各个状态。
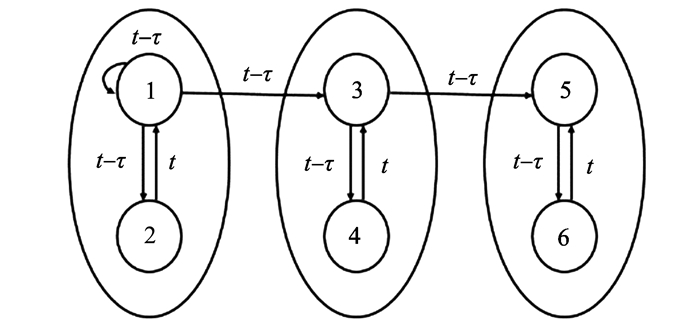
本研究在六维前馈神经网络模型中发现了很多以往的前馈网中没有发现的特性。具体模型的示意图如图 1所示。
|
图 1 六维前馈神经网络模型 Figure 1 Six dimensional feedforward neural network |
本研究首先将对所构建的前馈神经网络的动态特性进行分析。这里利用泛函微分方程理论对Pitchfork分支和1:1共振分支进行分析[9-12]。
(1) 余维一简单或双零的分支分析
零特征值的存在性使系统具有零奇异性(稳态分支,Bogdanov-Takens分支等)。幂零分支已被广泛研究。如果一个系统在临界点的特征矩阵具有单零或双零特征值,则幂零奇异可能发生。本研究主要讨论在具有时滞的前馈神经网络中的这种奇异性分支的产生。显然,(0, 0, 0, 0, 0, 0)为本研究所提出的方程的平衡点,对此方程在原点线性化方程为:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = - {x_1}\left( t \right) + a{x_2}\left( t \right) + b{x_1}\left( {t - \tau } \right)\\ {{\dot x}_2} = - \gamma {x_2}\left( t \right) + {x_1}\left( {t - \tau } \right)\\ {{\dot x}_3} = - {x_3}\left( t \right) + a{x_4}\left( t \right) + b{x_1}\left( {t - \tau } \right)\\ {{\dot x}_4} = - \gamma {x_4}\left( t \right) + {x_3}\left( {t - \tau } \right)\\ {{\dot x}_5} = - {x_5}\left( t \right) + a{x_6}\left( t \right) + b{x_3}\left( {t - \tau } \right)\\ {{\dot x}_6} = - \gamma {x_6}\left( t \right) + {x_5}\left( {t - \tau } \right) \end{array} \right., $ |
式中的τ为分支参数。此方程相应的特征方程为
| $ \Delta = {\Delta _1}\Delta _2^2 = 0, $ |
式中: Δ1=λ2+(γ+1)λ+γ-bλe-λτ-(γb+a)e-λτ,Δ2=λ2+(γ+1)λ+γ-aλ-λτ。
假定
条件1:γ=γb+a,a>0,0 < b < 1,
条件2:γ=a,-2 < b < 0,
则有如下定理。
定理1 如果条件1和条件2成立,则有:
(a) 如果条件1成立,则Δ=0的根λ=0重数为1,在原点线性化方程在平凡解处经历余维一的简单零分支。
(b) 如果条件2成立,则Δ=0的根λ=0重数为2。在原点线性化方程在平凡解处经历余维一的双零Pitchfork分支。
证明 假设在条件1和条件2下,Δ=0的所有根,除了λ=0具有负实部。λ=0作为Δ1=0或Δ2=0的根意味着γ=γb+a或者γ=a。横截条件成立如:
| $ \frac{{{\rm{d}}{\Delta _1}\left( \lambda \right)}}{{{\rm{d}}\lambda }}\left| {_{\lambda = 0}} \right. = 1 + \left( {a + b} \right)\tau ,\frac{{{\rm{d}}{\Delta _2}\left( \lambda \right)}}{{{\rm{d}}\lambda }}\left| {_{\lambda = 0}} \right. = 1 + a\tau 。$ |
由于f(x)=tanh x,本研究所构建的方程是对称的,因此,分支的类型是Pitchfork分支。
(2) 1:1共振Hopf分支分析
当线性系统的特征方程具有两对纯虚根时,如果其比值不是有理数则称为非共振,否则称为共振。最重要的共振是1:1非半单共振情形。本研究考虑每个节点具有相同的动力学性质的六维的前馈神经网络模型的1:1非半单共振Hopf分支,分析了神经元之间的耦合线性链的时间演化,每一个神经元被在其链中的前任动态驱动。研究发现,某些神经元可能会表现出强迫振子行为。该系统的这一特性可以检测和放大特定频率的信号[13]。文献[14]构造了非线性前馈网耦合振子模式,利用该振子固有的Hopf分支点附近的非线性响应,可以实现对频带宽度小信号的显著的放大作用。本研究结果与其提出的非线性耦合振子的前馈模式网络的试验研究结果相类似。
假设
条件3:0 < b < 1, a < 0,|γb+a| < γ < |a|。
定理2 如果条件3成立。在τ∈[0, τ0)时零解是渐近稳定。当τ=τj(j=0, 1, …)时零解经历Hopf分支。式中: ω=
证明 考虑Δ1=0,当τ=0时,Δ1=0的根为
| $ {\lambda _{1,2}} = \frac{{ - \left( {1 - b + \gamma } \right) \pm \sqrt {{{\left( {1 - b + \gamma } \right)}^2} - 4\left( {\gamma \left( {1 - b} \right) - a} \right)} }}{2} $ |
具有负实部。如果iω(ω>0)是Δ1=0根,将iω带入Δ1=0可得:
| $ - {\omega ^2} + {\rm{i}}\omega \left( {1 + \gamma } \right) + \gamma - {\rm{i}}\omega b{{\rm{e}}^{ - {\rm{i}}\mu \tau }} - \left( {\gamma b + a} \right){{\rm{e}}^{ - {\rm{i}}\mu \tau }} = 0, $ |
这意味着ω是不存在的。同理,考虑Δ2=0。当τ=0时,Δ2=0的根也具有负实部。接下来,令iω(ω>0)为Δ2=0的根,将iω带入Δ2=0可得:
| $ - {\omega ^2} + {\rm{i}}\omega \left( {1 + \gamma } \right) + \gamma - a{{\rm{e}}^{ - {\rm{i}}\mu \tau }} = 0, $ |
因此,
| $ \begin{array}{*{20}{c}} {\tau = \tau _j^ \pm \left( {j = 0,1, \cdots } \right):{{\left( {\frac{{{\rm{d}}{\mathop{\rm Re}\nolimits} \lambda \left( \tau \right)}}{{{\rm{d}}\tau }}} \right)}^{ - 1}}\left| {\tau = {\tau _j} = \left( {2\omega _ + ^4 - 2\omega \left( { - {\omega ^2} + {b^2} - {a^2}} \right)} \right)} \right./}\\ {{{\left( {4{\omega ^6} + \left( {{\omega ^2} - {\omega ^2}\left( {{\omega ^2} + {b^2} - {a^2}} \right)} \right)} \right)}^2} > 0,} \end{array} $ |
成立。
应用上述结论与泛函微分方程的分支定理,得到所构建的方程解的存在性和稳定性的结论:
如果条件3成立,当τ∈[0, τ0),零解渐进稳定。零解在τ=τj(j=0, 1, …)处经历Hopf分支。
考虑所构建的方程的1:1共振Hopf分支的产生条件。选取参数τ=τj(j=0, 1, …)做变换t→t/τ,此时构建的系统方程变为:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = - \tau {x_1}\left( t \right) + \tau a\tanh {x_2}\left( t \right) + \tau b\tanh \left[ {{x_3}\left( {t - 1} \right)} \right]\\ {{\dot x}_2} = - \tau \gamma {x_2}\left( t \right) + \tau {x_1}\left( {t - 1} \right)\\ {{\dot x}_3} = - \tau {x_3}\left( t \right) + \tau a\tanh {x_4}\left( t \right) + \tau b\tanh \left[ {{x_1}\left( {t - 1} \right)} \right]\\ {{\dot x}_4} = - \tau \gamma {x_4}\left( t \right) + \tau {x_3}\left( {t - 1} \right)\\ {{\dot x}_5} = - \tau {x_5}\left( t \right) + \tau a\tanh {x_6}\left( t \right) + \tau b\tanh \left[ {{x_3}\left( {t - 1} \right)} \right]\\ {{\dot x}_6} = - \tau \gamma {x_6}\left( t \right) + \tau {x_5}\left( {t - 1} \right) \end{array} \right., $ |
式中t和t-1分别为函数xi(i=0, 1, …)的自变量。选择相空间C=C([-1, 0], R6),对于任何Ø∈C,定义‖Ø‖=sup-1≤θ≤0 |Ø(θ)|,然后,则相空间C是具有上确界范数,从[-1, 0]到R6连续函数的Banach空间。对于Ø∈C,定义:
| $ {L_{0\emptyset }} = \int\limits_{ - 1}^0 {{\rm{d}}\eta \left( \theta \right)\emptyset \left( \theta \right)} , $ |
式中,η:[-1, 0]→R6×R1(R6和R1分别表示六维空间和一维空间)是分量有界变差的矩阵值函数,其定义为
| $ \eta \left( \theta \right) = \tau \mathit{\boldsymbol{A}}\delta \left( \theta \right) - \tau \mathit{\boldsymbol{B}}\delta \left( {\theta + 1} \right), $ |
式中,
| $ \delta \left( \theta \right) = \left\{ \begin{array}{l} 0,\theta \ne 0\\ 1,\theta = 0 \end{array} \right., $ |
| $ \mathit{\boldsymbol{A}} = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} { - 1}&a&0\\ 0&{ - \gamma }&0\\ 0&0&{ - 1} \end{array}}&{\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ a&0&0 \end{array}}\\ {\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ 0&0&0 \end{array}}&{\begin{array}{*{20}{c}} { - \gamma }&0&0\\ 0&{ - 1}&a\\ 0&0&{ - \gamma } \end{array}} \end{array}} \right), $ |
| $ \mathit{\boldsymbol{B = }}\left( {\begin{array}{*{20}{c}} b&0&0&0&0&0\\ 1&0&0&0&0&0\\ b&0&0&0&0&0\\ 0&0&1&0&0&0\\ 0&0&b&0&0&0\\ 0&0&0&0&1&0 \end{array}} \right)。$ |
线性方程可以写成:
| $ \dot X\left( t \right) = {L_0}{X_t}, $ |
| $ {X_t} = X\left( {t + \theta } \right), $ |
式中-1≤θ≤0。在C*×C(*表示共轭)上的双线性形式为
| $ \left\langle {\psi ,\varphi } \right\rangle = \psi \left( 0 \right)\varphi \left( 0 \right) - \int_{ - 1}^0 {\int_{\xi = 0}^\theta {\psi \left( {\xi - \theta } \right){\rm{d}}\eta \left( \theta \right)\varphi \left( \xi \right){\rm{d}}\xi } } , $ |
式中:
在条件3下,方程Δ1=0的根有负实部,因此,对于所有τ≥0方程:
在τ=τj(j=0, 1, …),由于x1和x2趋近于0,因此,方程:
由于B是幂零矩阵,且L_0的特征值是二重的,则当τ=τ_j(j=0, 1, …)时1:1共振Hopf分支发生。
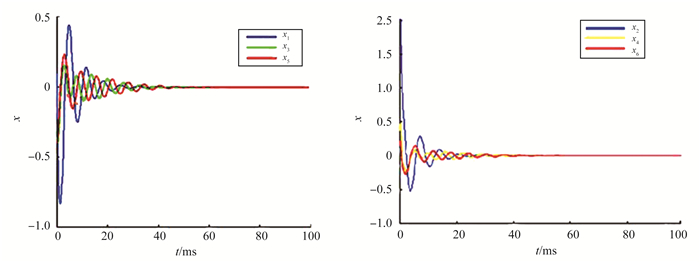
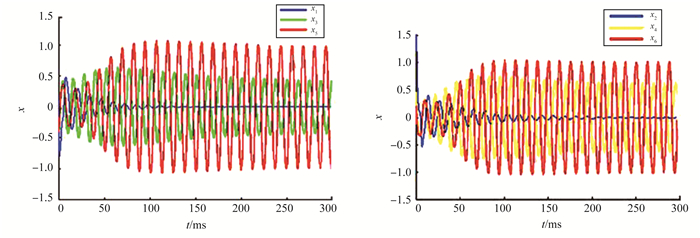
下面通过仿真试验分别给出振子1、3、5和振子2、4、6的振波图。其中,参数选择为γ=1.3,a=-1.6,b=0.25。如图 2所示,τ=1.5时振子1、3、5和振子2、4、6的振荡都是稳定的。在图 3中,当τ=4.5时,振子1和2仍然稳定,但振子3, 4, 5, 6开始不稳定,并出现周期解。通过上面的分析,振子5和振子6出现周期解的特征完全符合文献[14]中的结论,即具有周期解的模型可能具有图像增强作用。由此可得结论:当取值满足1:1共振发生时,本研究所构建的方程可以实现小信号增强,此动力学性质可用于图像增强。
|
图 2 当γ=1.3, a=-1.6, b=0.25, τ=1.5时各振子波形图 Figure 2 Waveform of each oscillator when γ=1.3, a=-1.6, b=0.25, τ=1.5 |
|
图 3 当γ=1.3, a=-1.6, b=0.25, τ=4.5时各振子波形图 Figure 3 Waveform of each oscillator when γ=1.3, a=-1.6, b=0.25, τ=4.5 |
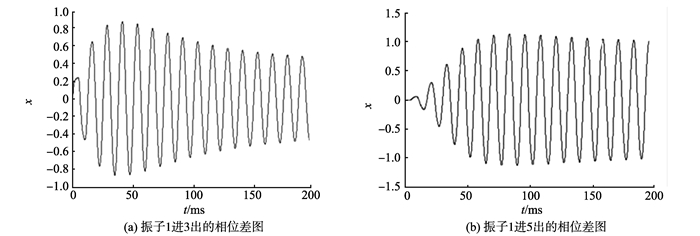
本研究利用相位差观察振幅的变化分析前馈神经网络模型在图像增强中的作用。由图 4可得出,振子3和振子5具有明显的增强作用,且相位差越高的时间点,增强效果越好。可见参数的选取对最终结果有非常重要的影响。因此,在图像增强处理试验中进行参数取值时,尽量取到相位差最高点对应的tspan值。为了验证模型在相位差最高点的图像增强效果,选取的灰度低对比度林火遥感图像的像素大小为572×336,仿真验证当γ=1.3, a=-1.6,b=0.25,τ=4.5时,将振子3和振子5分别作为模型输出时的效果。通过上面的理论分析可知,相位差图中最高的峰值点对应的tspan有最好的增强效果。这里按照图 4的相位差图为将振子3作为输出的模型分别取tspan=28.1和tspan=41.2;为振子5作为输出的模型取tspan=58.5和tspan=71.1。通过图 5的仿真效果可以验证,模型在tspan取相位差中最高点的增强效果最好。从图像增强后的视觉效果对比中可知,将振子5作为输出的模型的图像增强更突出。
|
图 4 相位差图 Figure 4 Phase difference diagram |

|
图 5 振子5作为输出的模型增强效果对比 Figure 5 Comparison of the model enhancement effect of oscillator 5 as output |
本研究分别利用低对比度的灰度和彩色林火遥感图像进行图像增强仿真试验,并与灰度变换增强和传统直方图均衡化函数增强方法进行效果对比。
试验的具体流程为:首先,将输入图像均一化处理,其中用x=1代表白色,x=0代表黑色,其他的灰度级别在[0, 1]之间变化,因此,振子1、2、3、…、6的最大值为1;然后将待处理的图像作为初值输入给振子1,初值的形式为(xij, 0, 0, 0, 0, 0),其中,xij表示输入图像的各像素点;最后,经过模型的迭代运算,在第5个振子输出结果图像。
3.1 灰度图像增强方法仿真效果比较图像增强包括提高图像的清晰度和对比度。提高对比度可以使灰度图像中黑白两极分化更加明显。对比度越高图像的细节表现得越好,高对比度图像非常有利用图像的分割处理。林火遥感图像一般会包含很多噪声,因此,在进一步处理之前往往需要先对其进行滤波处理。但是滤波处理又会造成图像对比度低,边缘模糊的问题。针对这一问题,本研究选取经过滤波处理后的灰度林火遥感图像进行增强处理,并与灰度变换增强和传统直方图均衡化函数增强方法进行效果比较。具体效果如图 6所示。

|
图 6 各增强方法效果对比 Figure 6 Contrast of the enhancement methods |
灰度变换增强方法和传统直方图均衡化方法的增强效果并不理想。灰度变换增强方法只能通过整体地对图像的灰度值进行变换来达到增强的效果,并不能真正地实现对比度增强,尤其会削弱一部分目标对象的边缘。利用直方图均衡化函数的增强方法虽然可以使图像变清晰,但是图像对比度并不高,图像边缘仍不够明显。低维前馈神经网络算法虽然在计算量上比六维的前馈神经网络要少,但增强效果确远远不如六维前馈神经网络的增强效果。经过与一些经典的图像增强算法相比,可知利用本研究提出的图像增强算法处理后,图像的对比度显著提高,林火区域轮廓清晰。
为了进一步更客观地分析图像的增强效果,本研究利用图像均值、标准差和图像信息熵的值进行评价[15-17]。
图像均值可以评价图像的整体亮度。图像的均值变大,说明增强后的图像整体变亮,反之说明图像稍暗。计算公式为
| $ {\rm{mean}} = \frac{1}{m}\sum\limits_i {ip\left( i \right)} . $ |
图像对比度可以通过图像的标准差来衡量。图像标准差越大,则说明图像对比度越高,目标对象的轮廓越清晰。图像的标准差计算方法为:对于向量xi,其中i=1, 2, …, n,标准差
| $ s = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{x}}} \right)}^2}} } , $ |
式中,x=
香农信息理论中,图像的信息熵表征图像的灰度分布的聚集特性,单位为比特/像素,代表图像信息源的平均信息量。图像的信息熵越大,说明该图像信息量越多,其计算式为
| $ I = - \sum\limits_{i = 0}^{255} {p\left( i \right) * \ln p\left( i \right)} , $ |
式中:p(i)表示灰度级i的像素概率,一般取大于0的数值。当p(i)=0,则按p(i)*lnp(i)=0计算。
由表 1可知,利用本研究增强算法处理后的图像均值和标准差最大。均值大说明增强后的图像亮度大,增强效果最显著。标准差最大,则说明对比度最高。信息熵代表着图像的信息含量。从表 1可以看出,利用本研究算法处理的图像信息熵值最小。信息熵低主要是本算法增强了图像对比度和亮度,减少了边缘以外的一些不必要的信息。所以,无论从主观评价还是客观的数据分析上,本研究提出的基于具有时滞的六维前馈神经网络模型的图像增强算法对低对比度灰度林火遥感图像的增强处理非常有效。
| 表 1 灰度图像增强效果定量分析表 Table 1 Quantitative analysis table of gray image enhancement effect |
下面进一步验证本研究提出的增强算法对彩色图像增强的有效性。本研究同样选取像素大小为756×756的低对比度RGB彩色林火遥感图像作为原图像。为了达到更好的彩色图像增强效果,本研究首先将仿真图像从RGB模型转换为HSV模型,经过模型处理后再将结果图像转换为RGB模型。HSV模型是一种主观模型,在HSV模型下进行彩色图像的增强,可以使彩色图像在亮度明暗的调节上效果更加显著。
将图像从RGB模型转换为HSV模型表示为
| $ \left\{ \begin{array}{l} V = \left( {R + G + B} \right)/3\\ S = 1 - \frac{3}{{\left( {R + G + B} \right)}}\left[ {\min \left( {R,G,B} \right)} \right]\\ H = {\cos ^{ - 1}}\left( {\frac{{\left[ {\left( {R - G} \right) + \left( {R - B} \right)} \right]/2}}{{{{\left( {R - G} \right)}^2}\left( {R - B} \right){{\left( {R - G} \right)}^{\frac{1}{2}}}}}} \right)/360 \end{array} \right.。$ |
如图 7所示,通过仿真效果可以看出,利用本研究增强算法处理后的彩色图像更加清晰,对比度也显著提高,整个图像的视觉效果明显优于另外两种方法。下面本研究再利用HSV直方图对各增强后的图像进行增强效果分析。

|
图 7 几种增强方法效果对比 Figure 7 Contrast of the enhancement methods |
下面利用公式计算增强后的彩色图像均值、标准差及信息熵来进行的客观分析。
由表 2可知,利用本研究增强算法处理后的彩色图像均值最大,均值大说明增强后的图像亮度大,增强效果最显著。标准差也比较大,说明对比度也较高。从数据整体上分析,各数据分布比较合理。因此,本研究提出的基于具有时滞的六维前馈神经网络模型的图像增强算法对低对比度彩色林火遥感图像的增强处理也非常有效。
| 表 2 彩色图像增强效果定量分析表 Table 2 Quantitative analysis table for color image enhancement effect |
因为彩色图像比灰度图像包含更多的数据信息,为了更好地评价彩色图像的增强效果,本研究利用颜色矩进一步进行客观分析[18]。
颜色的分布可以通过颜色矩来描述。低阶矩上主要是颜色的分布信息,因此,图像的颜色分布通常用一阶矩、二阶矩和三阶矩来表达。其中,每个颜色分量平均强度可以用一阶来表示;二阶矩表示待测区域的颜色方差,即不均匀性;三阶矩表示颜色分量的偏斜度,即颜色的不对称性。一阶矩、二阶矩和三阶矩的定义分别为
| $ \left\{ \begin{array}{l} {\mu _i} = \frac{1}{N}\sum\limits_{j = 1}^N {{I_{ij}}} \\ {\sigma _i} = {\left[ {\frac{1}{N}\sum\limits_{j = 1}^N {{{\left( {{I_{ij}} - \mu } \right)}^2}} } \right]^{\frac{1}{2}}}\\ {\zeta _i} = {\left[ {\frac{1}{N}\sum\limits_{j = 1}^N {{{\left( {{I_{ij}} - \mu } \right)}^3}} } \right]^{\frac{1}{3}}} \end{array} \right., $ |
式中:第j个像素的第i个颜色分量用Iij表示;N是像素数量。
由表 3可知,根据颜色特征值分析,通过Histeq函数和Imadjust函数增强的彩色图像的一阶矩值虽然比低对比度图像的一阶矩值高,但是与本研究增强算法处理后的图像的一阶矩值相比还是低很多。一阶矩的值代表图像的整体亮度,可见本研究增强算法的亮度提升最大,效果最突出。颜色二阶矩值代表各颜色分量的分布是否均匀。从计算结果来看,本研究算法的值也较高。颜色三阶矩值代表各颜色分量的颜色偏斜度,从表中的值可以看出,本研究算法的各颜色分量的值偏斜方向与原低对比度彩色图像相比差异最大。因此可以证明,本研究增强算法对低对比度彩色图像的增强效果优于其他几种增强算法。
| 表 3 彩色图像颜色矩分析表 Table 3 Color moment analysis table of color image |
综上所述,利用具有时滞的六维前馈神经网络模型的图像增强算法无论是对灰度图像还是彩色图像都能达到非常好的图像增强效果,即使对如遥感图像这类纹理复杂图像的增强效果也非常显著,且效果优于文中提到的其他几种的增强方法。
| [1] | COHENM A, GROSSBERG S. Absolute stability of global pattern formation and parallel memory storage by competitive neural networks[J]. IEEE Transactions on Systems Man & Cybernetics, 1983, 13(5): 815-826 |
| [2] | HOPFIELDJ J. Neurons with graded response have collective computational properties like those of two-state neurons[J]. Proceedings of the National Academy of Sciences of the United States of America, 1984, 81(10): 3088-92 DOI:10.1073/pnas.81.10.3088 |
| [3] | SONG Y, WEI J. Local hopf bifurcation and global periodic solutions in a delayed predator-prey system[J]. Journal of Mathematical Analysis & Applications, 2005, 301(1): 1-21 |
| [4] | LI L, YUAN Y. Dynamics in three cells with multiple time delays[J]. Nonlinear Analysis Real World Applications, 2008, 9(3): 725-746 DOI:10.1016/j.nonrwa.2006.12.015 |
| [5] | WANG H, JIANG W. Hopf-pitchfork bifurcation in van der pol's oscillator with nonlinear delayed feedback[J]. Journal of Mathematical Analysis & Applications, 2010, 368(1): 9-18 |
| [6] | JIANGW, NIU B. On the coexistence of periodic or quasi-periodic oscillations near a hopf-pitchfork bifurcation in NFDE[J]. Communications in Nonlinear Science & Numerical Simulation, 2013, 18(3): 464-477 |
| [7] | RUANS G, FILFIL R S. Dynamics of a two-neuron system with discrete and distributed delays[J]. Physica D Nonlinear Phenomena, 2004, 191(3-4): 323-342 DOI:10.1016/j.physd.2003.12.004 |
| [8] | WANG H, WANG J. Hopf-pitchfork bifurcation in a two-neuron system with discrete and distributed delays[J]. Mathematical Methods in the Applied Sciences, 2015, 38(18): 4967-4981 DOI:10.1002/mma.3418 |
| [9] | PAN Y, YU H. Biomimetic hybrid feedback feedforward neural-network learning control[J]. IEEE Transactions on Neural Networks & Learning Systems, 2017(99): 1-7 |
| [10] | HU J Y, ZHANG J S, ZHANG C X, et al. A new deep neural network based on a stack of single-hidden-layer feedforward neural networks with randomly fixed hidden neurons[J]. Neurocomputing, 2016, 171(C): 63-72 |
| [11] | PAYAL A, RAI C S, REDDY B V R. Analysis of some feedforward artificial neural network training algorithms for developing localization framework in wireless sensor networks[J]. Wireless Personal Communications, 2014, 82(4): 1-18 |
| [12] | MASULLI P, VILLAA E P. Dynamics of evolving feed-forward neural networks and their topological invariants[M]. Barcelona, Spain: Springer International Publishing, 2016: 25-46. |
| [13] | WANG P, LU J H, ZHANG Y H. Global relative input-output sensitivities of the feed-forward loops in genetic networks[J]. Neurocomputing, 2012, 78(1): 155-165 DOI:10.1016/j.neucom.2011.05.034 |
| [14] | MCCULLENN J, MULLIN T, GOLUBITSKY M. Sensitive signal detection using a feed-forward oscillator network[J]. Physical Review Letters, 2007, 98(25): 254101 DOI:10.1103/PhysRevLett.98.254101 |
| [15] |
褚江, 陈强, 杨曦晨. 全参考图像质量评价综述[J].
计算机应用研究, 2014, 31(1): 13-22 CHU Jiang, CHEN Qiang, YANG Xichen. A review of all reference image quality evaluation[J]. Computer Application Research, 2014, 31(1): 13-22 DOI:10.3969/j.issn.1001-3695.2014.01.003 |
| [16] |
王哲远, 李元祥, 郁文贤. SAR图像质量评价综述[J].
遥感信息, 2016, 31(5): 1-10 WANG Zheyuan, LI Yuanxiang, YU Wenxian. SAR image quality assessment overview[J]. Remote Sensing Information, 2016, 31(5): 1-10 DOI:10.3969/j.issn.1000-3177.2016.05.001 |
| [17] |
王志明. 无参考图像质量评价综述[J].
自动化学报, 2015, 41(6): 1062-1079 WANG Zhiming. Overview of no reference image quality assessment[J]. Automation Journal, 2015, 41(6): 1062-1079 |
| [18] |
李俊峰. 基于RGB色彩空间自然场景统计的无参考图像质量评价[J].
自动化学报, 2015, 41(9): 1601-1615 LI Junfeng. No reference image quality assessment based on RGB color space natural scene statistics[J]. Automation Journal, 2015, 41(9): 1601-1615 |




