2. 贵州省公共大数据重点实验室, 贵州 贵阳 550025
2. Guizhou Provincial Key Laboratory of Public Big Data, Guiyang 550025, Guizhou, China
随着互联网的快速发展, 网络上产生了大量的短文本, 如新闻网站的标题、腾讯空间的说说、新浪微博、百度知识问答、商品评论等。短文本理解, 尤其是短文本主题发现对于获取用户观点、监测突发性事件等具有重要作用。然而, 发现短文本的主题信息是不容易的。直接用传统的主题模型处理短文本效果不佳, 主要原因是短文本字数有严格限制(140字符以内), 使短文本存在特征稀疏的特点。除此之外, 短文本还具有书写随意、噪音大等特点, 这些特点都严重干扰了短文本的主题发现过程。
近年来, 短文本理解受到了广泛关注。针对短文本的特征稀疏问题, 许多研究者利用聚合方法与知识库方法丰富短文本的表示。聚合方法是指将字数较少的短文本聚合起来形成伪长文本用于短文本分析。Weng等[1]将每个推特用户发送的推特信息聚合为一篇长文本, 然后利用传统的潜在狄利克雷分配(latent dirichlet allocation, LDA)模型[2]发现推文主题。Hong和Davison[3]利用被聚合的推特信息提出了多种方法训练标准主题模型, 并且比较这些方法的性能和有效性。基于知识库的方法利用大量的外部资源丰富短文本的内容。Gabrilovich[4]借助Wikipedia增加短文本的语义特征, 丰富短文本语料库。Hotho等[5]将Wordnet加入短文本聚类过程中。Phan等[6-7]构建了包含Wikipedia知识库的短文本分类器框架。Hu等[8]将来自原始文本的内部语义信息与来自Wikipedia和WordNet的外部概念相结合改善短文本的聚类性能。Sahami等[9]通过使用搜索引擎丰富短文本的信息, 引入基于网页的核函数衡量短文本片段之间的相似度。
除上述两类方法外, 近些年提出了一些新的方法。Yan等[10]提出了biterm topic model(BTM), 该模型直接对语料库中的共现词建模, 从而发现短文本的主题。Yin和Wang[11]将整个短文本语料库视为一个主题分布, 提出了利用吉布斯采样的狄利克雷多项混合(gibbs sampling for dirichlet multinomial mixture, GSDMM)模型, 极大地提高了短文本的聚类效果。Seifzadeh等[12]使用统计语义学进行短文本主题挖掘。Wang[13]等将深度表示学习与半监督相结合进行短文本理解。
利用长文本的主题知识提高短文本主题发现效果的一个相关领域是迁移学习[14]。迁移学习主要研究如何将相关领域的辅助信息迁移到目标领域中, 从而帮助目标领域的学习和研究。Jin等[15]提出了二元潜在狄利克雷分配(dual latent dirichlet allocation, DLDA)主题模型, 该模型将长文本与短文本相结合, 联合学习长文本辅助主题和短文本目标主题。然而, DLDA模型忽略了长短文本数据源不相同的问题, 使用了相同的主题分配先验参数。
为了更加有效地挖掘短文本主题, 本研究提出了从长文本迁移主题知识用于短文本主题发现的思想, 该思想的提出主要有以下两个原因:第一, 与短文本相比, 长文本具有非常丰富的词语信息, 并且以LDA模型为代表的传统主题模型在挖掘和理解以新闻为代表的长文本主题方面已经收到了良好的效果。第二, 实际生活中很方便收集与短文本主题相关的长文本信息, 例如, 新浪微博上讨论的一些热门话题通常也会出现在新浪推送的新闻中; 网页的搜索片段一般都与某些网站的内容相关联。基于以上思想, 本研究提出了基于狄利克雷多项回归(dirichlet-multinomial regression, DMR)模型[16]的二元狄利克雷多项回归(dual dirichlet-multinomial regression, DDMR)模型, 其中DMR模型是基于LDA的一个先进的主题模型。DDMR模型与DLDA模型迁移长文本主题知识的方法不同, DLDA模型认为长短文本拥有各自的主题空间与主题对词语的分配比例, 短文本集中的词语既可以通过短文本集的主题-词语分布生成, 也可以通过长文本集的主题-词语分布生成。DDMR模型假设长文本集与短文本集共享相同的主题空间以及主题对词语的分配比例, 短文本集中词语通过两者共同的主题-词语分布生成, 使短文本可以借助长文本中大量与自身主题相关的词语改善短文本的主题发现效果。考虑到长短文本具有不同的数据来源, 采用DMR方法产生长短文本各自的主题分配狄利克雷先验参数。
1 二元狄利克雷多项回归模型 1.1 符号与术语w是文本的基本单元, 是词汇表{1, 2, …, V}中的一项。一篇文本d由N个词组成, 表示为d=[w1 w2 … wN], 其中wn是该序列中的第n个词。一个类型标识因子x用于区分文章的长短类型, 其中x∈{0, 1}, x=1时为长文本, x=0时为短文本; 对于文本类型向量, 长文本类型向量为xL=[1 0]T, 短文本类型向量为xS=[1 0]T。一个数据集D由两部分组成, 第一部分是由ML篇文章组成的长文本集DL, dl为DL中第l篇长文本, l∈{1, 2, …, ML}; 第二部分是由MS篇文章组成的短文本集DS, ds为DS中第s篇短文本, s∈{1, 2, …, MS}。
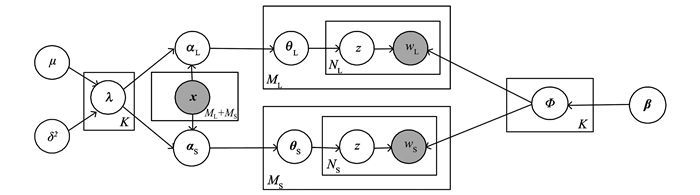
1.2 DDMR模型DDMR模型是一个概率生成模型, 其基本思想是:(1)长短文本具有相同的主题-词语分布, 即共享相同的主题空间和主题对词语的分配比例; (2)每一篇文本, 不论是长文本还是短文本, 能够用一个主题分布表示。其中, DMR对主题分布的狄利克雷先验参数建模, 使得两类文本具有不同的先验参数, 从而产生不同的主题分配。DDMR的生成模型如图 1所示。
|
图 1 DDMR模型的图形化表示 Figure 1 Graphical representation of DDMR model |
对于数据集中的ML+MS篇文本, DDMR模型假设如下的生成过程:
(1) 对于主题k∈{1, …, K}
① 选择λk~N(μ, δ2I); ②选择ϕk~Dirichlet(β); ③计算αLk=exp(xLTλk)与αSk=exp(xLTλk)。
(2) 对于任意一篇文本dj
① 选择T~Poisson (ζ)。②选择θn~Dirichlet(αL), 其中, dj∈DL; 选择θn~Dirichlet(αS), 其中, dj∈DS。③对于文本中dj的每一个词语wi, 选择主题zi~Multinomial(θn); 选择词语wi~Multinomial(wi|zi, ϕ)。
其中:N是均值μ, 协方差矩阵为δ2I的二维高斯分布; 对于每一个主题k, λk是向量, 其维度与文本类型向量xL和xS相同; Dirichlet(·)是狄利克雷分布; αL和αS分别为长文本集和短文本集的狄利克雷分布的主题先验参数, αL的每一个元素为αLk, αS的每一元素为αSk; Multinomial(·)为多项分布, θn为多项分布的参数, 表示文本dj的主题分布; β是狄利克雷分布的词语先验参数, 该向量的每一个元素值均为β; ϕk表示主题为k的词语的分布。
根据模型的生成过程, 可以写出所有已知变量和隐藏变量的联合分布。每一篇长文本dl的联合分布
| $ \begin{gathered} p\left( {\mathit{\boldsymbol{\lambda }}, {\mathit{\boldsymbol{x}}_{\text{L}}}, {\mathit{\boldsymbol{\alpha }}_{\text{L}}}, {\mathit{\boldsymbol{\theta }}_n}, \mathit{\boldsymbol{z}}, {\mathit{\boldsymbol{d}}_l}, \boldsymbol{\mathit{\phi}} |\mathit{\boldsymbol{\mu }}, {\sigma ^2}, \mathit{\boldsymbol{\beta }}} \right) = p\left( {\mathit{\boldsymbol{\lambda }}|\mu, {\sigma ^2}} \right)p\left( {{\mathit{\boldsymbol{\alpha }}_{\text{L}}}|\mathit{\boldsymbol{\lambda }}, {\mathit{\boldsymbol{x}}_{\text{L}}}} \right)p\left( {{\mathit{\boldsymbol{\theta }}_n}|{\mathit{\boldsymbol{\alpha }}_{\text{L}}}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\prod\limits_{i = 1}^{\left| {{\mathit{\boldsymbol{d}}_l}} \right|} {P\left( {{z_i}|{\mathit{\boldsymbol{\theta }}_n}} \right)p\left( {{w_i}|{z_i}, \boldsymbol{\mathit{\phi}} } \right)p\left( {\boldsymbol{\mathit{\phi}} |\mathit{\boldsymbol{\beta }}} \right)} 。\\ \end{gathered} $ |
每一篇短文本ds的联合分布
| $ \begin{array}{l} p\left( {\mathit{\boldsymbol{\lambda }}, {\mathit{\boldsymbol{x}}_{\rm{S}}}, {\mathit{\boldsymbol{\alpha }}_{\rm{S}}}, {\mathit{\boldsymbol{\theta }}_n}, \mathit{\boldsymbol{z}}, {\mathit{\boldsymbol{d}}_s}, \boldsymbol{\mathit{\phi}} |\mathit{\boldsymbol{\mu }}, {\sigma ^2}, \mathit{\boldsymbol{\beta }}} \right) = p\left( {\mathit{\boldsymbol{\lambda }}|\mu, {\sigma ^2}} \right)p\left( {{\mathit{\boldsymbol{\alpha }}_{\rm{S}}}|\mathit{\boldsymbol{\lambda }}, {\mathit{\boldsymbol{x}}_{\rm{S}}}} \right)p\left( {{\mathit{\boldsymbol{\theta }}_n}|{\mathit{\boldsymbol{\alpha }}_{\rm{S}}}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\prod\limits_{i = 1}^{\left| {{\mathit{\boldsymbol{d}}_s}} \right|} {P\left( {{z_i}|{\mathit{\boldsymbol{\theta }}_n}} \right)p\left( {{w_i}|{z_i}, \boldsymbol{\mathit{\phi}} } \right)p\left( {\boldsymbol{\mathit{\phi}} |\mathit{\boldsymbol{\beta }}} \right)} 。\end{array} $ |
需要注意的是, λ是元素值为λk的矩阵, 其中k∈{1, 2, …, K}。在给定参数μ和δ2的前提下, p(λ|μ, δ2)为一个定值, 在首次初始化时为高斯分布的采样值。在实际的算法操作中, λ根据当前的主题分配不断更新, 从而使得p(αS|λ, xS)不断更新, 在这一点上, DDMR优于DLDA模型。DLDA模型的先验参数α是提前给定的, 在实际算法操作中也是不更新的。p(θn|α)和p(ϕ|β)是狄利克雷分布, p(zi|θn)p(wi|zi, ϕ)表示给定主题分布θn和主题-词语分布ϕ的条件下选定一个词的概率。
2 算法对于DDMR模型, 利用随机期望最大化(stochastic expectation maximization, SEM)算法[17]推断长文本与短文本潜在的主题结构。SEM算法如下:
(1) E-步。在给定可观测词语和特征的条件下, 使用Gibbs方法从当前的先验分布中采样主题的分配值。Gibbs采样公式见2.1节。
(2) M-步。在给定主题分配的前提下, 使用有限内存BFGS(limited-memory BFGS, L-BFGS)方法[18]优化参数λ。关于λ的似然函数与梯度见2.2节。
当算法趋于收敛状态之后, 估计多项分布的参数θ和ϕ见2.3节。
2.1 Gibbs采样公式(1) 对于每个词语wi∈dl∈DL, 选择一个主题z的公式为
| $ p\left( {{z_i} = z|{\mathit{\boldsymbol{z}}_{-i}}, {\mathit{\boldsymbol{d}}_l}, \mu, {\sigma ^2}, \mathit{\boldsymbol{\lambda }}, {\mathit{\boldsymbol{x}}_{\rm{L}}}, \mathit{\boldsymbol{\beta }}} \right) \propto \frac{{\exp \left( {\mathit{\boldsymbol{x}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_z}} \right) + {n_{l, z}}-1}}{{\sum\limits_{k = 1}^K {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right) + {n_{l, k}}-1} }} \cdot \frac{{{n_{z, i}} + {\beta _t} - 1}}{{\sum\limits_{t = 1}^V {{n_{z, t}} + {\beta _t} - 1} }}, $ | (1) |
式中: z∈{1, 2, …, K}; z-i为当前文本中除去词语wi后剩余词语的主题集合; nl, z为长文本dl中主题为z的词语的个数; nz, i是长短文本混合集中主题为z的词语wi的个数。
(2) 对于每个词语wi∈ds∈DS, 选择一个主题z的公式为
| $ p\left( {{z_i} = z|{\mathit{\boldsymbol{z}}_{-i}}, {\mathit{\boldsymbol{d}}_s}, \mu, {\sigma ^2}, \mathit{\boldsymbol{\lambda }}, {\mathit{\boldsymbol{x}}_{\rm{S}}}, \mathit{\boldsymbol{\beta }}} \right) \propto \frac{{\exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_z}} \right) + {n_{s, z}}-1}}{{\sum\limits_{k = 1}^K {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right) + {n_{s, k}}-1} }} \cdot \frac{{{n_{z, i}} + {\beta _t} - 1}}{{\sum\limits_{t = 1}^V {{n_{z, t}} + {\beta _t} - 1} }}, $ | (2) |
式中ns, z是长文本ds中主题为z的词语的个数。
2.2 优化参数λ(1) 参数λ的对数似然函数
| $ \begin{array}{l} \log P\left( {\mathit{\boldsymbol{z}}, \mathit{\boldsymbol{\lambda }}} \right) = \sum\limits_l {\left( {\log \boldsymbol{\mathit{\Gamma}} \left( {\sum\limits_k {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right)} } \right)-\log \boldsymbol{\mathit{\Gamma}} \left( {\sum\limits_k {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right) + {n_l}} } \right)\\ + \sum\limits_k {\left( {\log \boldsymbol{\mathit{\Gamma}} \left( {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right) + {n_{l, k}}} \right)-\log \boldsymbol{\mathit{\Gamma}} \left( {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right)} \right)} \right)} } \right)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_s {\left( {\log \boldsymbol{\mathit{\Gamma}} \left( {\sum\limits_k {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right)} } \right)-\log \boldsymbol{\mathit{\Gamma}} \left( {\sum\limits_k {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{L}}{\mathit{\boldsymbol{\lambda }}_k}} \right) + {n_s}} } \right) + } \right.} \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_k {\left( {\log \boldsymbol{\mathit{\Gamma}} \left( {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right) + {n_{s, k}}} \right) - \log \boldsymbol{\mathit{\Gamma}} \left( {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right)} \right)} \right)} } \right) -\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \sum\limits_k {\sum\limits_f {\left( {\frac{1}{2}\log \left( {2\pi {\sigma ^2}} \right) + \frac{{\lambda _{fk}^2}}{{2{\sigma ^2}}}} \right), } } \end{array} $ | (3) |
式中: nl是长文本dl中词语的个数; nl, k为长文本dl中主题为k的词语的个数; λfk是主题为k时向量λk中的元素, λfk∈{λLk, λSk}, 其中λLk表示主题为k且为长文本类型, λSk表示主题为k且为短文本类型, 当λfk为λLk时, a=1, b=0, λfk为为λSk时, a=0, b=1; Ψ(·)为digamma函数。
(2) 参数λ的梯度函数
| $ \begin{array}{l} \frac{{\partial \log P\left( {\mathit{\boldsymbol{z}}, \mathit{\boldsymbol{\lambda }}} \right)}}{{\partial {\lambda _{fk}}}} = \sum\limits_l {a \cdot \exp \left( {\mathit{\boldsymbol{x}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right)} \mathit{\Psi} \left( {\sum\limits_k {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right)}-\\ \;\;\;\;\;\;\;\;\;\;\;\mathit{\Psi} \left( {\sum\limits_k {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right) + {n_l}} } \right) + } \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\mathit{\Psi} \left( {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right) + {n_{j, k}}} \right)-\mathit{\Psi} \left( {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right)} \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_s {b \cdot \exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right) \cdot \mathit{\Psi} \left( {\sum\limits_k {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right)}-\\ \;\;\;\;\;\;\;\;\;\;\;\mathit{\Psi} \left( {\sum\limits_k {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right) + {n_s}} } \right) + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\left. {\mathit{\Psi} \left( {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right) + {n_{s, k}}} \right) - \mathit{\Psi} \left( {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right)} \right)} \right) - \frac{{{\lambda _{fk}}}}{{{\sigma ^2}}}。\end{array} $ | (4) |
(1) 主题-词语分布
| $ {\boldsymbol{\mathit{\phi}} _{k, t}} = \frac{{{n_{k, t}} + {\beta _t}}}{{\sum\limits_{v = 1}^V {{n_{k, v}} + {\beta _v}} }}, $ | (5) |
式中nk, t为长短文本混合集中主题为k的词语t的个数。
(2) 文本-主题分布
| $ {\theta _{s, k}} = \frac{{\exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_k}} \right) + {n_{s, k}}}}{{\sum\limits_{z = 1}^K {\exp \left( {\mathit{\boldsymbol{x}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_z}} \right) + {n_{s, z}}} }}\prod\limits_k {\frac{1}{{\sqrt {2\pi } {\sigma ^2}}}} \exp \left( {\frac{{\lambda _{{\rm{S}}k}^2}}{{2{\sigma ^2}}}} \right), $ | (6) |
式中: ns, k是文本ds中主题为k的词语的个数, 其中文本ds的主题为{θs, 1, θs, 2, …, θs, K}中最大值对应的主题k的值。
3 试验结果及分析 3.1 试验数据集本研究采用两个真实的文本语料库生成试验所用的数据集。第一个语料库为Reuters-25178, 该语料库包含25 178篇文章, 共135个主题, 每篇文章至少属于一个主题。选择主题分别为“grain”“money-fx”“trade”和“interest”的文章形成Reuters-25178语料库的子集。第一个试验数据集, 即Reuter_k4数据集来源于这个子集。Reuter_k4数据集由短文本和长文本两部分组成。随机地从上述子集中选择1 800篇新闻文本并提取这些文本的标题作为Reuter_k4数据集的短文本集, 同时提取这些文本的正文作为Reuter_k4数据集的长文本集。
第二个语料库是文献[19]中提出的AMiner-Paper。该语料库包含2 092 356篇研究型论文, 分为“graphical image”“computer network”和“database”三个研究领域。第二个试验的数据集称为AMPaper_k3, 从AMiner-Paper语料库的3个主题下选择11 450篇文章的标题作为AMPaper_k3的短文本集, 同时将摘要部分作为AMPaper_k3的长文本集。
对两个数据集进行预处理。两个数据集总结如表 1所示。
| 表 1 数据集介绍 Table 1 Description of datasets |
本研究中采用归一化互信息(normalized mutual information, NMI)作为主题聚类性能的评估标准[20]。对于给定的数据集, 共有I条数据, 算法得到的聚类结果为X=(x1, x2, …, xI), 标准的类别标签为Y=(y1, y2, …, yI), 则NMI的计算方法为
| $ {\rm{NMI}}\left( {X, Y} \right) = 2\frac{{\sum\limits_i {\sum\limits_j {\frac{{\left| {{x_i} \cap {y_j}} \right|}}{N}\log \frac{{N\left| {{x_i} \cap {y_j}} \right|}}{{\left| {{x_i}} \right|\left| {{y_j}} \right|}}} } }}{{-\left( {\sum\limits_i {\frac{{\left| {{x_i}} \right|}}{N}\log \frac{{\left| {{x_j}} \right|}}{N}} + \sum\limits_j {\frac{{\left| {{y_j}} \right|}}{N}\log \frac{{\left| {{y_j}} \right|}}{N}} } \right)}}。$ |
NMI为0~1, NMI越高说明聚类效果越好。
3.3 试验设置DDMR模型需要初始化两个参数。对于所有的数据集, 设置β=0.01, δ=0.5。λ是一个矩阵, 通过高斯函数初始化。设置每次试验的迭代次数为2 000, 且每一次迭代都优化λ。根据式(6), 选取短文本ds的主题分布θs, k中最大概率对应的主题为该短文本的主题。针对每次试验, 运行程序10次。对10次NMI得分取平均值作为最终的试验结果。将DDMR模型与下列3个模型进行比较:(1)LDA_S:基线方法。不使用辅助长文本数据集, 直接利用短文本学习LDA主题模型。(2)LDA_LS。首先使用辅助长文本学习LDA模型, 其次在短文本上进行推理。(3)DLDA。一个先进的主题模型, 该模型通过从辅助长文本数据上迁移知识来帮助短文本聚类。
对于所有的对比试验, 设置α向量中每个元素值为0.5, β=0.01。
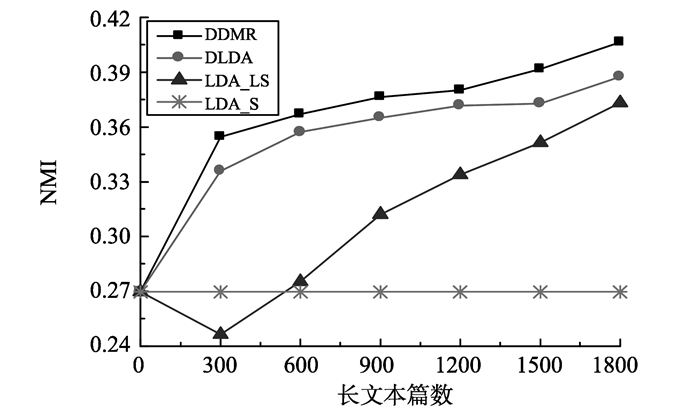
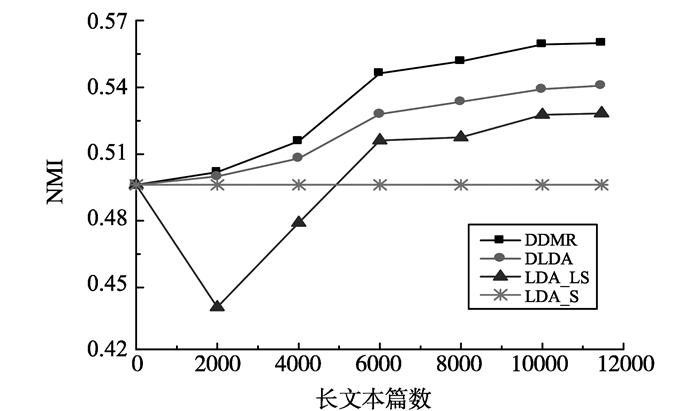
3.4 试验结果与分析 3.4.1 辅助长文本数量图 2、3分别展示了针对Reuter_k4数据集和AMPaper_k3数据集的试验结果。通过改变辅助长文本的数量, 比较DDMR模型、DLDA模型、LDA_LS模型以及LDA_S模型的聚类效果。该试验中, Reuter_k4数据集的主题数目是4, AMPaper_k3数据集的主题数目为3。
|
图 2 Reuter_k4数据集各模型的聚类效果 Figure 2 Clustering effect of all models on the Reuter_k4 |
|
图 3 AMPaper_k3数据集各模型的聚类效果 Figure 3 Clustering effect of all models on the AMPaper_k3 |
由图 2、3可知:当长文本数量为0时, 所有的模型降为仅使用短文本集的LDA模型, 由于短文本的特征稀疏问题, 所有模型都得到了较差的性能。当长文本数量增加时, DDMR和DLDA的NMI值逐渐增加, 其中DDMR比DLDA效果更好, 说明本研究提出的长文本和短文本从带有相关但不相同先验参数的主题分布中产生的思想是有用的。与DDMR和DLDA直接利用长短混合文本学习模型参数θ和ϕ相比, LDA_LS首先利用长文本学习模型参数, 其次利用这些参数推断短文本的主题结构。当使用少量的长文本时, LDA_LS由于训练长文本数据集不足, 估算的参数无法准确推断短文本的主题, 因而得到了比LDA更差的主题发现效果。随着长文本数量的增加, LDA_LS模型逐渐学习到相对准确的主题参数, 主题发现效果得到较大提升。因此, 利用从长文本发现的高质量主题知识能够改善短文本中词语的理解。显然, 加入任何数量的长文本, DDMR模型相比其他模型实现了更好的主题发现效果。
3.4.2 判别词判别词是能够明显区别类别的词语。根据式(5), 选择各主题下概率最大的前10个词语作为模型发现的判别词。表 2、3分别列出了Reuter_k4和AMPaper_k3数据集各主题下的10个判别词。
| 表 2 Reuter_k4数据集DDMR和LDA_S模型发现的判别词 Table 2 Discriminative terms for the DDMR and LDA_S model on the Reuter_k4 dataset |
| 表 3 AMPaper_k3数据集DDMR和LDA_S模型发现的判别词 Table 3 Discriminative terms for the DDMR and LDA S model on the AMPaper_k3 dataset |
由表 2、3可知, DDMR模型可以捕获与主题相关的关键性词语, 而LDA_S的捕获能力稍弱。例如:对于Reuter_k4数据集的主题“grain”, DDMR的判别词大都为与谷物相关度较高的词汇, 例如:“wheat”“crop”和“agricultur”等, 而LDA_S的判别词中包含有“reserv”和“tender”这些主题相关度相对较低的词汇。对于AMPaper_k3数据集的主题“graphic image”, DDMR可以发现“interact”“video”等有意义的词汇, 而LDA_S不能发现这些词汇。
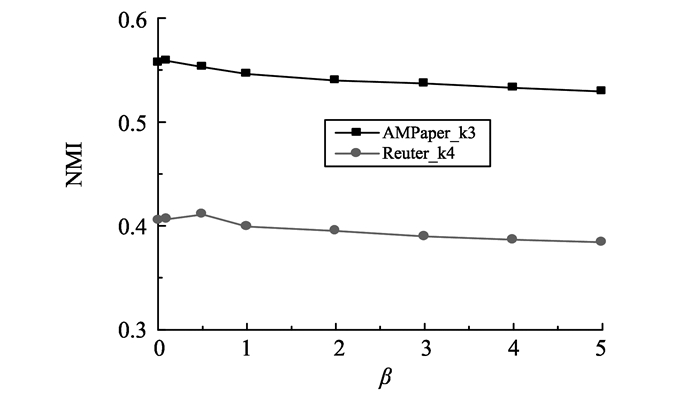
3.4.3 超参数β和δ图 4、5分别展示了超参数β和δ对DDMR模型聚类效果的影响。在DDMR的生成模型中, β是长短文本的连接点, 表明长短文本共享相同的主题和词语信息, 是长文本辅助短文本的基础。试验中, β取值为0.01、0.1、0.5、1、2、3、4和5。δ作为高斯分布的参数之一, 当δ设置不同的初始值, 通过高斯分布随机采样, 得到不同的λ, 进而影响狄利克雷多项分布的参数α向量中的每一项, 最终影响模型对主题的选择倾向。设置δ取值为0.01、0.1、0.5和1。对于所有的试验, 设置μ=0, Reuter_k4数据集的主题数目为4, AMPaper_k3数据集的主题数目为3。
|
图 4 β对DDMR模型聚类效果的影响 Figure 4 The influence of β on clustering effect of DDMR model |
|
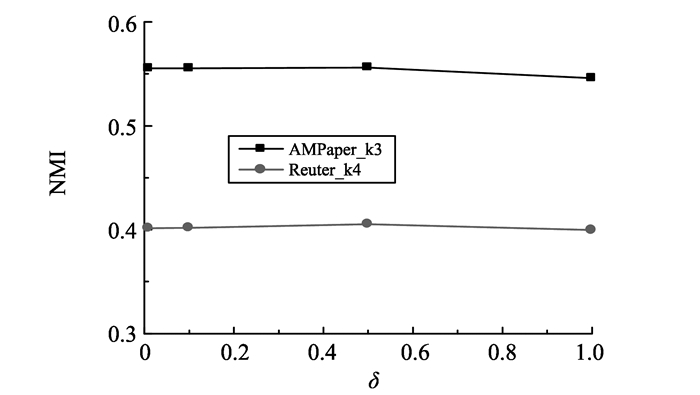
图 5 δ对DDMR模型聚类效果的影响 Figure 5 The influence of δ on clustering effect of DDMR model |
从图 4可知, 当β变化时, 对于不同的数据集, DDMR模型可以实现较为稳定的聚类性能, β对于试验效果影响不大。当β < 0.5时, DDMR模型展现出相对较好的聚类性能。因此, 试验设置β为0.01。由图 5可知, 对于两个数据集, 当δ取不同的初始值时, DDMR模型的聚类效果是稳定的。δ仅会影响模型对主题的首次选择, 而不会影响选择过程, 原因是除了初始输入之外, DDMR模型使用SEM方法交替采样主题分配与参数λ优化。试验结果的稳定性表明δ的选择是健壮的。因此, 设置δ为0.5。
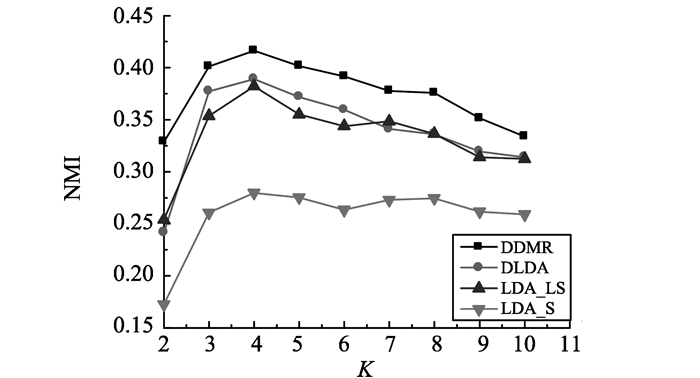
3.4.4 主题数量K传统的LDA主题模型假设主题数量提前已知。然而, 现实生活中给定大量的文章, 用户很难推断真实的主题数量。针对Reuter_k4数据集, 讨论当K取不同的值时, DDMR模型的聚类性能, 设置K=2~10。在所有的试验设置中, 辅助长文本的数量为1 800篇。分别讨论DDMR、DLDA、LDA_LS、LDA_S的聚类性能。试验结果如图 6所示。由图 6可知, K设置为真实的类数量时, 即K=4, 所有的模型实现了最好的聚类性能。当K小于真实的类数量时, LDA_S、LDA_LS、DLDA明显比DDMR模型差。当K大于真实的类数量时, 所有模型的NMI具有缓慢下降的趋势, 但DDMR实现了最好的聚类效果。因此, 当真实的类数量未知时, 轻微地放大或缩小主题数量的真实值的做法是可行的。
|
图 6 K对各模型聚类效果的影响 Figure 6 The influence of K on clustering effect of all models |
DDMR模型假设长文本与短文本的主题是相关的, 本试验讨论长文本集对DDMR的聚类效果的影响。使用3个额外的数据集, 分别为Reuter_r1, Reuter_r2, 和Reuter_r3。这3个数据集的短文本部分, 使用与Reuter_k4数据集相同的短文本集。对于长文本部分, 在不限制与短文本主题相关的前提下, 从Reuters-25178语料库中随机选择任意文本的正文部分形成一个背景数据集。选择长文本分两个步骤:(1)从与短文本主题相关的长文本中随机选择相关长文本; (2)从背景数据集中随机选择无关长文本。Reuter_r1、Reuter_r2和Reuter_r3数据集的相关长文本数量和无关长文本数量之和为1 800篇。将相关长文本数量除以长文本的总篇数得到相关度比例。设置3个数据集的相关度比例为0.3、0.6和1。在以下的试验中, 设置K=4、β=0.01、δ=0.5。针对这3个数据集, 通过变化加入数据集中的长文本的数量, 讨论长文本集对DDMR模型进行短文本主题发现造成的影响。试验结果如图 7所示。
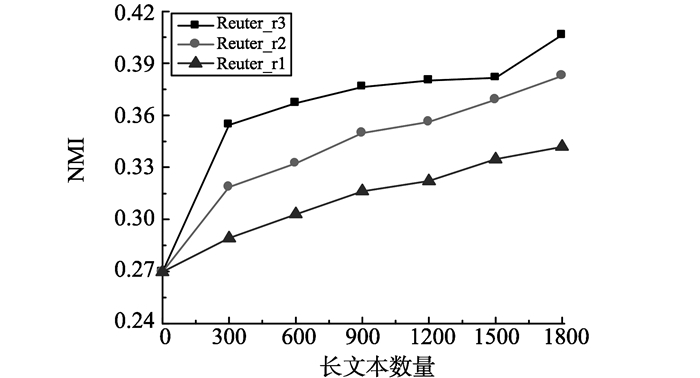
|
图 7 长文本集对DDMR模型聚类效果的影响 Figure 7 The influence of long text set on clustering effect ofDDMR model |
从图 7可知, 使用不同相关度的数据集后, 当文章数量不为0时, DDMR模型的NMI不断增长。因此, 可以得出结论:长文本与短文本的相关度越高, 短文本的聚类性能越好, 即改善长文本的质量有助于加强短文本的聚类效果。对于同一个数据集, 增加长文本的数量, 短文本的聚类效果也会提高。因此, 当长文本有一定数量的噪声数据时, 增加长文本的数量是改善短文本主题发现的有效方法。
4 结语本研究提出了一个用于短文本理解的DDMR主题模型, 试验通过对长文本数量和相关度的讨论, 证明加入主题相关的辅助长文本能够提高短文本的主题发现效果。该模型的不足之处在于主题数量必须提前已知。在实际生活中, 给定大量的短文本, 用户很难准确估计主题的数量。因此, 在主题数量未知的情况下, 使用长文本辅助短文本进行短文本理解是未来的研究方向。
| [1] | WENG J, LIM E P, JIANG J, et al. Twitter Rank: finding topic-sensitive influential twitterers[C]//Proceedings of the third ACM International Conference on Web Search and Data Mining. New York, USA: ACM, 2010: 261-270. https://dl.acm.org/citation.cfm?id=1718520 |
| [2] | BLEI D M, NG A Y, JORDAN M I. Latent dirichlet allocation[J]. Journal of Machine Learning Research, 2003, 3: 993-1022 |
| [3] | HONG L, DAVISON B D. Empirical study of topic modeling in Twitter[C]//Proceedings of the first Workshop on Social Media Analytics. New York, USA: ACM, 2010: 80-88. https://dl.acm.org/citation.cfm?doid=1964858.1964870 |
| [4] | GABRILOVICH E. Feature generation for textual information retrieval using world knowledge[J]. ACM, 2007, 41(2): 123-123 |
| [5] | HOTHO A, STAAB S, STUMME G. Ontologies improve text document clustering[C]//Proceedings of the third IEEE International Conference on Data Mining. Washington, D C, USA: IEEE Computer Society, 2003: 541-544. https://ieeexplore.ieee.org/document/1250972/ |
| [6] | PHAN X H, NGUYEN C T, LE DT, et al. A hidden topic-based framework toward building applications with short web documents[J]. IEEE Transactions on Knowledge & Data Engineering, 2011, 23(7): 961-976 |
| [7] | PHAN X H, NGUYEN L M, HORIGUCHI S. Learning to classify short and sparse text & web with hidden topics from large-scale data collections[C]//Proceedings of the 17th International Conference on World Wide Web. New York, USA: ACM, 2008: 91-100. |
| [8] | HU X, SUN N, ZHANG C, et al. Exploiting internal and external semantics for the clustering of short texts using world knowledge[C]//Proceedings of the 18th ACM Conference on Information and Knowledge Management. New York, USA: ACM, 2009: 919-928. https://dl.acm.org/citation.cfm?doid=1645953.1646071 |
| [9] | SAHAMI M, HEILMAN T D. A web-based kernel function for measuring the similarity of short text snippets[C]//Proceedings of the 15th International Conference on World Wide Web. New York, USA: ACM, 2006: 377-386. https://www.semanticscholar.org/paper/A-web-based-kernel-function-for-measuring-the-of-Sahami-Heilman/3a472b537a04ec7d477d441c96841d7da56e6a9a |
| [10] | YAN X, GUO J, LAN Y, et al. A biterm topic model for short texts[C]//Proceedings of the 22nd International Conference on World Wide Web. New York, USA: ACM, 2013: 1445-1456. |
| [11] | YIN J, WANG J. A dirichlet multinomial mixture model-based approach for short text clustering [C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2014: 233-242. https://dl.acm.org/citation.cfm?doid=2623330.2623715 |
| [12] | SEIFZADEH S, FARAHAT A K, KAMEL M S, et al. Short-textclustering using statistical semantics[C]//Proceedings of the 24th International Conference on World Wide Web. New York, USA: ACM, 2015: 805-810. |
| [13] | WANG Z, MI H, ITTYCHERIAH A. Semi-supervised clustering for short text via deep representation learning[C]//Proceedings of the 20th SIGNLL Conference on Computational Natural Language Learning. Stroudsburg, USA: ACL, 2016: 31-39. |
| [14] | RAINA R, NG A Y, KOLLER D. Constructing informative priors using transfer learning[C]//Proceedings of the 23rd International Conference on Machine learning. New York, USA: ACM, 2006: 713-720. |
| [15] | JIN O, LIU N N, ZHAO K, et al. Transferring topical knowledge from auxiliary long texts for short text clustering[C]//Proceedings of the 20th ACM International Conference on Information and Knowledge management. New York, USA: ACM, 2011: 775-784. https://dl.acm.org/citation.cfm?doid=2063576.2063689 |
| [16] | MIMNO D, MCCALLUM A. Topic models conditioned on arbitrary features with dirichlet-multinomial regression[C]//Proceedings of the 24th Conference on Uncertainty in Artificial Intelligence. Corvallis, Oregon, USA: AUAI Press, 2012: 411-418. |
| [17] | CELEUX G, DIEBOLT J. The SEM algorithm: a probabilistic teacher algorithm derived from the EM algorithm for the mixture problem[J]. Computationalstatistics Quarter, 1985(2): 73-82 |
| [18] | LIU D C, NOCEDAL J. On the limited memory BFGS method for large scale optimization[J]. Mathematical Programming, 1989, 45(3): 503-528 |
| [19] | TANG J, ZHANG J, YAO L, et al. ArnetMiner: extraction and mining of academic social networks[C]//Proceedings of the 14th ACM SIGKDD International Conference on Knowledge discovery and Data Mining. New York, USA: ACM, 2008: 990-998. |
| [20] | ZHONG S. Semi-supervised model-based document clustering: a comparative study[J]. Machine Learning, 2006, 65(1): 3-29 DOI:10.1007/s10994-006-6540-7 |




