2. 河北经贸大学信息技术学院, 河北 石家庄 050061;
3. 深圳大学计算机与软件学院, 广东 深圳 518060
2. College of Information & Technology, Hebei University of Economics and Business, Shijiazhuang 050061, Hebei, China;
3. College of Computer Science & Software Engineering, Shenzhen University, Shenzhen 518060, Guangdong, China
TIRKEL A Z等人[1]提出了数字水印的概念。孙圣和等人[2]也指出, 数字水印技术是通过在数字产品中嵌入秘密信息来保护数字产品的版权、证明产品的真实可靠性、跟踪盗版行为或提供产品的附加信息。研究人员已经提出了大量的数字水印算法[3-7]。向数字产品中加入水印, 会改变数字产品, 温泉等人[8]提出了零水印技术, 不修改数字产品, 而利用数字产品特征来构造水印(零水印)。
零水印技术是当前的研究热点之一, 已经出现了大量针对视频[9-10]、音频[11-12]、文本[13-14]、图像[15-18]等数字产品的零水印算法。文献[8]利用高阶累积量提取的图像特征来构造零水印, 但计算时间较长。文献[19]利用哈希值作为原始医疗图像的特征来构造零水印。文献[20]利用离散小波变换(DWT)和矩阵范数计算抗打印扫描攻击的不变特征值构造零水印。文献[21]将BP神经网络应用于零水印的构造中。文献[22]将宿主图像分成4*4的子块, 奇异值分解每一子块, 利用U分量相邻系数大小关系保持不变的特征构造水印。但是文献[8]和文献[19-22]提出的算法, 只构造了鲁棒水印, 没有构造半脆弱水印来对待检测图像进行篡改检测。肖振久等人[23]利用超混沌技术, 构造了医学图像篡改定位零水印, 但还需要提高算法抵抗噪声攻击的能力。
零水印质量需要提取原始图像的关键特征来保障, 且零水印算法应具有较强的抗攻击能力, 考虑到这一点, 本研究设计的算法中采用了DWT、SVD和DCNN。与空域算法相比, 变换域算法中水印鲁棒性更强。DWT克服了离散傅里叶变换(discrete fourier transform, DFT)固定分辨率的缺点, 也克服了离散余弦变换(discrete cosine transform, DCT)纯粹将空域变换到频率域和重构图像时容易出现马赛克现象的缺点。SVD可以表示图像内在的代数特征, 稳定性非常好。DCNN通过卷积能够获取图像的关键特征。
1 算法相关技术介绍 1.1 奇异值分解设矩阵Am×n∈Crm×n (r>0), 其中m≥n, 则A的奇异值分解式[2]为:
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{US}}{\mathit{\boldsymbol{V}}^{\rm{T}}} = \sum\limits_{i = 1}^n {{\sigma _i}{u_i}v_i^{\rm{T}}} , $ | (1) |
式中: U、V为正交矩阵; S为非对角线元素都为0的矩阵; σi=
卷积神经网络(CNN)由LECUN Y等人[24]提出, 是一种多层前馈网络。当网络有多个卷积层、下采样层时, 就构成了深度卷积神经网络(DCNN), DCNN一般由输入层、多个卷积层(C层)和下采样层(S层)、输出层构成。
DCNN的训练分为2个阶段:前向传播阶段和反向传播阶段。
(1) 前向传播阶段。指由输入层向输出层的传播过程。在输入层输入样本, 经过若干个卷积神经网络层, 最后在输出层采用全连接输出特征图, 将输出的特征图与期望的标签特征图比较, 得到误差值, 如果误差值在设定的允许误差范围内, 则训练结束, 否则进入反向传播阶段。
单层卷积神经网络的训练由卷积、非线性变换和下采样3个阶段完成。卷积和非线性阶段:输入卷积层的每个特征图与卷积核进行卷积, 即采用局部权值共享方式连接, 并加上偏置项, 再经过非线性阶段(此阶段使用激活函数)。下采样阶段:对非线性阶段输入的特征图进行平均池化、最大池化或窗移等操作。
(2) 反向传播阶段。将误差值采用梯度下降的方式逐层向前传递, 权值更新式(2)为:
| $ \begin{array}{*{20}{c}} {\omega {'}_{ji}^l = \omega _{ji}^l - \alpha \frac{{\partial E}}{{\partial \omega _{ji}^l}} = \omega _{ji}^l + \Delta \omega _{ji}^l,}\\ {b{'}_j^l = b_j^l - \alpha \frac{{\partial E}}{{\partial b_j^l}} = b_j^l + \Delta b_j^l,} \end{array} $ | (2) |
式中:ωjil和ω′jil分别是更新前后的权重; E是误差值; α表示学习率; bjl和b′jl分别是更新前后的偏置。
2 基于SVD和DCNN的彩色图像多功能零水印算法算法分为构造零水印图像算法和提取零水印图像算法。
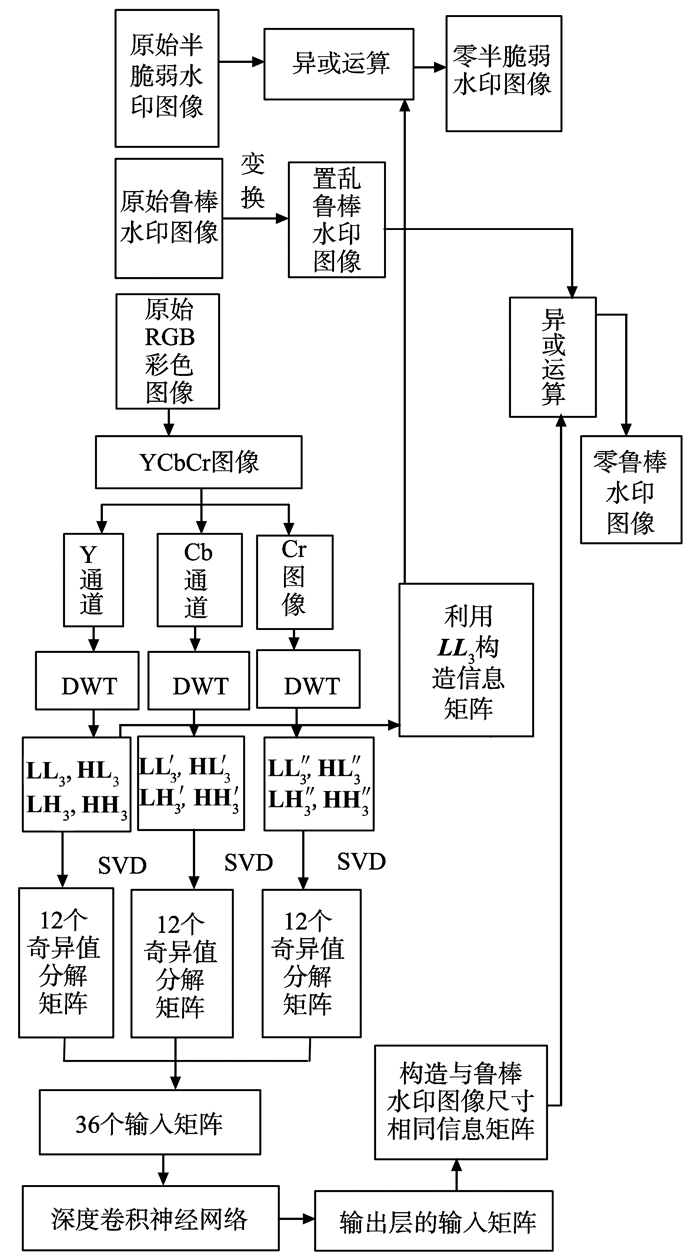
2.1 构造零水印算法构造零水印图像过程如图 1所示。
|
图 1 基于SVD和DCNN的彩色图像多功能构造零水印图像算法框图 Figure 1 The block diagram of multipurpose zero watermarking construction algorithm for color imagebased on SVD and DCNN |
(1) 对原始彩色图像进行转换。读出原始图像, 将其转换为RCbCr图像, 并分解出Y、Cb、Cr通道。
(2) 读出鲁棒水印图像, 并利用Arnold变换进行置乱。
(3) 读出半脆弱水印图像。
(4) 对原始图像的Y、Cb、Cr通道分别进行三尺度的“db1”离散小波变换, 并进行奇异值分解。Y、Cb、Cr通道小波变换后第三层的子带小波系数矩阵分别为LL3, HL3, LH3, HH3; LL′3, HL′3, LH′3, HH′3和LL″3, HL″3, LH″3, HH″3。对这12个矩阵进行奇异值分解, 共得到36个二维矩阵。
(5) 构造DCNN的输入矩阵和输出标签矩阵。将步骤(4)中得到的36个矩阵转换成尺度为偶数的方阵。将Y、Cb、Cr通道中得到的方阵尺度最大值赋值给m, 创建m×m×36的特征矩阵X, 其每个面为Xn(n=1, 2, …, 36), 分别将步骤(4)中得到的36个矩阵, 赋值给Xn, 就得到了输入特征矩阵。将X1的前36列, 每列之和除以X1元素总个数, 可得尺寸为1×36的输出标签矩阵T。
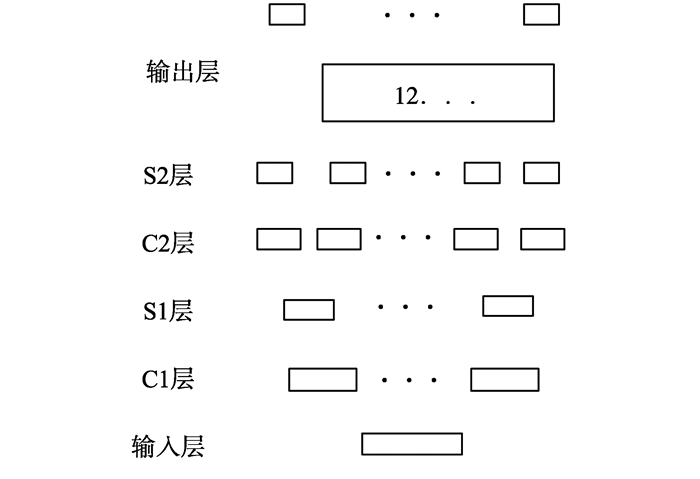
(6) 建立的DCNN如图 2所示。
|
图 2 深度卷积神经网络结构示意图 Figure 2 Structural diagram of DCNN |
图 2的DCNN由输入层、卷积层1(C1层)、下采样层1(S1层)、卷积层2(C2层)、下采样层2(S2层)、输出层组成。卷积层所用卷积核的尺寸都为5×5, C1层和C2层分别输出18个和36个矩阵; S1层和S2层分别将C1层和C2层传递的矩阵尺寸降为原来的1/4。
(7) 对DCNN进行训练。训练分正向阶段和反向阶段。
① 正向阶段
(a) 输入层。输入X为一个大小为m×m的36个特征图, 即为m×m×36的矩阵。
(b) 卷积层(C1层和C2层)。对卷积层(l层)的第j个输出特征图, 计算公式[25]为
| $ Y_j^l = \sigma \left( {\sum\limits_{i \in M_j^l} {X_j^{l - 1} * K_{ji}^l} + b_j^l} \right), $ | (3) |
式中:Mjl表示输入特征图的索引集合; Kjil为大小为5×5的卷积核; “*”代表卷积操作; σ为sigmoid函数。C1层和C2层分别输出18个(m-4)×(m-4)×36和36个
(c) 下采样层(S1层和S2层)。计算下采样层第j个输出特征图[25]
| $ Y_j^l = \beta _j^l{\rm{down}}\left( {Y_j^{l - 1}} \right) + b_j^l, $ | (4) |
式中:βjl为常数权重[0.25, 0.25, 0.25, 0.25], down(·)表示下采样。通过窗移, 得到下采样层的输出特征图。S1层和S2层分别得到18个
(d) 输出层。将S2层的输出转换成一维矩阵, 作为输出层的输入矩阵, 输出层的第j个单元输出
② 反向传播训练
(a) 输出层的误差传递。设输出层为L层, 输出层(全连接)的梯度
| $ \frac{{\partial {E^n}}}{{\partial {\omega _{kj}}}} = - \delta _k^Ly_j^{\left( {L - 1} \right)}, $ | (5) |
式中:ωkj为(L-1)层j单元与L层k单元的连接权重; δkL=(ok-tk)ok(1-ok), 为L层第k个单元的灵敏度; ok为L层第k个单元的输出; tk为L层第k个单元的期望输出。输出层的权重更新为
| $ \Delta {\omega _{kj}} = \alpha \delta _k^Ly_j^{\left( {L - 1} \right)} = \alpha \left( {{o_k} - {t_k}} \right){o_k}\left( {1 - {o_k}} \right)y_j^{\left( {L - 1} \right)}, $ | (6) |
式中:α为学习率; yj(L-1)为(L-1)层第j个单元的输出, 也是L层第j个单元对应的输入。
(b) 采样层误差传递。S2层的误差传递:S2层的后一层是全连接层, 其梯度计算式为
| $ \frac{{\partial {E^n}}}{{\partial {\omega _{ji}}}} = \delta _j^{\left( {L - 1} \right)}y_i^{\left( {L - 2} \right)}, $ | (7) |
式中:δj(L-1)为(L-1)层第j个单元的灵敏度。
(c) S1层的误差传递。S1层的后一层为卷积层(C2层), 其权重βj和偏置bj的梯度计算式
| $ \frac{{\partial {E^n}}}{{\partial {\beta _j}}} = \sum\limits_{u,v} {{{\left( {\delta _j^{\left( {L - 3} \right)}d_j^{\left( {L - 3} \right)}} \right)}_{uv}}} ,\frac{{\partial {E^n}}}{{\partial {b_j}}} = \sum\limits_{u,v} {{{\left( {\delta _j^{\left( {L - 3} \right)}} \right)}_{uv}}} , $ | (8) |
式中:δj(L-3)为灵敏度, dj(L-3)为C1层输出特征图下采样后得到的特征图。δj(L-3)和dj(L-3)的计算式[25]分别为
| $ \begin{array}{*{20}{c}} {\delta _j^{\left( {L - 3} \right)} = \sigma '\left( {x_j^{\left( {L - 3} \right)}} \right)。}\\ {{\rm{conv2}}\left( {\delta _j^{\left( {L - 2} \right)},{\rm{rot180}}\left( {k_j^{\left( {L - 2} \right)}} \right),{\rm{'full'}}} \right),} \end{array} $ | (9) |
式中:“
| $ d_j^{\left( {L - 3} \right)} = {\rm{down}}\left( {y_j^{\left( {L - 4} \right)}} \right)。$ | (10) |
本算法中, 采样层的连接权重和偏置都采用常数, 不需要调整, 只是向其上层传递误差。
(d) 卷积层的误差传递。卷积层l的δjl计算式[25]为
| $ \delta _j^l = \beta _j^{\left( {l + 1} \right)}\left( {\sigma '\left( {{\rm{net}}_j^l} \right) \cdot {\rm{up}}\left( {\delta _j^{\left( {l + 1} \right)}} \right)} \right), $ | (11) |
式中:βj(l+1)为下采样因子, 是常数; σ′(netjl)表示卷积层l的激活值netjl求导; up(·)表示上采样。
卷积层l的kjil和βjl梯度计算式[25]为
| $ \frac{{\partial {E^n}}}{{\partial k_{ji}^l}} = \sum\limits_{u,v} {{{\left( {\delta _j^l} \right)}_{uv}}{{\left( {p_i^{\left( {l - 1} \right)}} \right)}_{uv}}} ,\frac{{\partial {E^n}}}{{\partial b_j^l}} = \sum\limits_{u,v} {{{\left( {\delta _j^l} \right)}_{uv}}} 。$ | (12) |
式中:pi(l-1)表示净激活neti(l-1)在卷积时与kjil元素相乘的图像块。
(8) 获取用于构造零鲁棒水印图像的信息矩阵。取出S2层输出的矩阵F, 取F中每一个100行j列(j=1, 2, …, 36)为一组, 记作第i组, 计算其平均值。创建大小为36×36的矩阵G, 如果F第50行j列的元素大于第i组元素平均值, 则G的[i, j]元素为1, 否则为0, 得到的G为用于构造零鲁棒水印的信息矩阵。
(9) 构造零鲁棒水印图像。将步骤(8)获得的G和原始鲁棒水印进行异或运算, 则产生零鲁棒水印图像。
(10)获取用于构造半脆弱水印图像的信息矩阵。当LL3(i, j)≥LL3((i+1), j)≥LL3((i+2), j)时, 信息矩阵的元素为1, 否则为0, 形成与半脆弱水印尺寸相等的信息矩阵。
(11)构造零半脆弱水印图像。将信息矩阵和原始半脆弱水印进行异或运算, 产生零半脆弱水印图像。
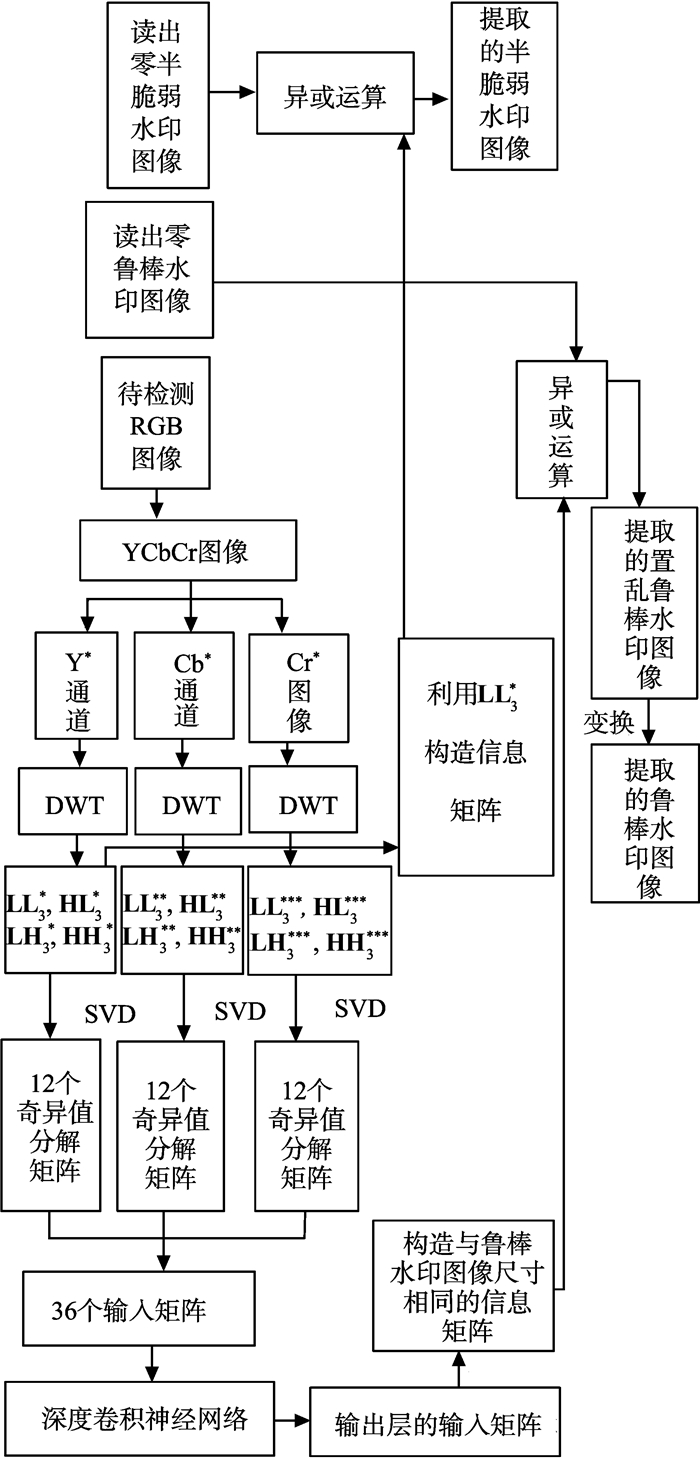
2.2 提取零水印算法提取零水印图像的过程如图 3所示。
|
图 3 基于SVD和DCNN的彩色图像多功能提取零水印图像算法框图 Figure 3 The block diagram of multipurpose zero watermarking extraction algorithm for color image based on SVD and DCNN |
提取步骤如下:
(1) 读出零鲁棒水印图像。
(2) 读出零半脆弱水印图像。
(3) 读出待检测图像, 转换成YCbCr图像, 并分解出Y*、Cb*、Cr*通道。
(4) 对待检测图像的Y*、Cb*、Cr*通道分别进行三尺度的“db1”离散小波变换, 并进行奇异值分解。过程同2.1步骤(4)。
(5) 构造DCNN的输入矩阵和输出标签矩阵。过程同2.1步骤(5)。
(6) 建立如图 2所示的DCNN。
(7) 对DCNN进行训练。训练过程同2.1步骤(7)。
(8) 构造用于提取鲁棒水印图像的信息矩阵。过程同2.1步骤(8)。
(9) 提取鲁棒水印图像。将2.2步骤(8)获取的信息矩阵和零鲁棒水印进行异或运算, 提取出置乱的鲁棒水印图像, 利用Arnold变换进行反置乱, 则得到提取的鲁棒水印图像。
(10)构造用于提取半脆弱水印图像的信息矩阵。过程同2.1步骤(10)。
(11)提取半脆弱水印图像。将2.2步骤(10)得到的信息矩阵和零半脆弱水印进行异或运算, 则得到提取的半脆弱水印图像。
3 仿真试验与分析 3.1 仿真试验算法采用MATLAB仿真实现。原始图像为512×512×3的RGB彩色图像, 鲁棒水印和半脆弱水印都采用自制的像素灰度值只有0和255的图像, 大小分别为36×36和64×64, 鲁棒水印置乱次数为30次。所采用的原始图像和水印图像如图 4所示。

|
图 4 原始图像和水印图像 Figure 4 Original image and watermarking image |
构造的零鲁棒水印图像和零半脆弱水印图像如图 5所示。

|
图 5 零鲁棒水印图像和零半脆弱水印图像 Figure 5 Zero robust watermarking image and zero semi-fragilewatermarking image |
提取的水印图像与原始水印图像相似度用归一化互相关(normalised cross-correlation, NC)表示, 不相似度用篡改评估函数(tamper assessment function, TAF)表示。原始图像未受攻击时, 提取的水印图像和半脆弱水印图像篡改定位图如图 6所示。提取的鲁棒水印图像和半脆弱水印图像的NC都为1, 提取的半脆弱水印图像的TAF=0。

|
图 6 提取的水印图像和篡改定位图 Figure 6 Extracted watermarking image and extracted watermarkingtamper location image |
本研究对原始图像进行了剪切、拼贴、压缩、滤波、噪声、旋转等攻击试验。拼贴攻击分两种, 拼贴1攻击是指从图像本身裁剪一部分进行拼贴攻击, 拼贴2攻击是从其它图像裁剪一部分进行的拼贴攻击。图 7为受到拼贴1攻击后的图像、提取出的水印图像及半脆弱水印图像篡改定位图, 拼贴比例为待检测图像的3.891 4%。

|
图 7 拼贴1攻击后的图像、提取出的水印图像和篡改定位图 Figure 7 Image after the first collage attacks, watermarking imageand tamper location image |
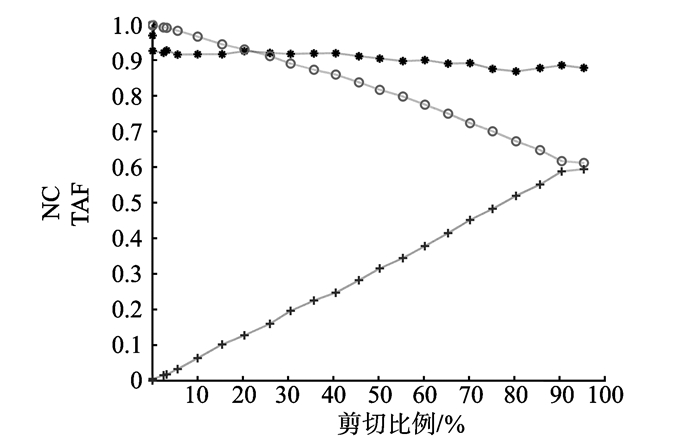
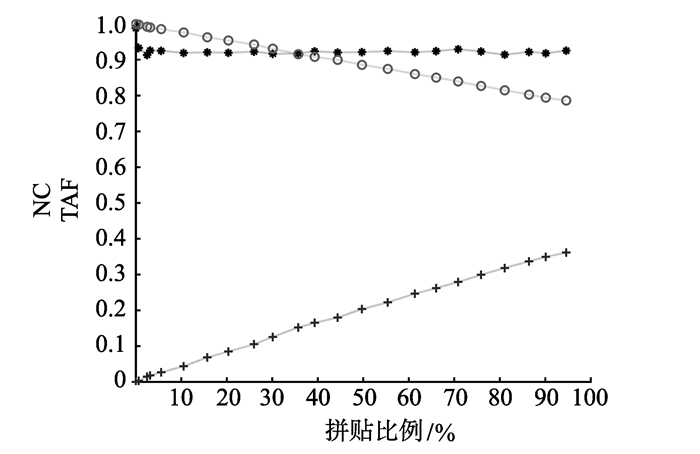
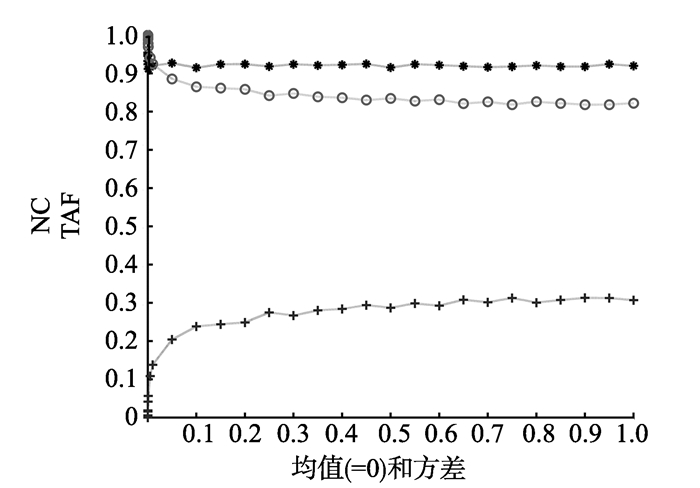
剪切、拼贴1、拼贴2、压缩、中值滤波、高斯噪声、椒盐噪声、旋转等常见攻击试验的结果如图 8~15所示。图中“


|
图 8 剪切攻击试验结果 Figure 8 Experimental results of cropping attacks |
|
图 9 拼贴1攻击试验结果 Figure 9 Experimental results of the first collage attacks |
|
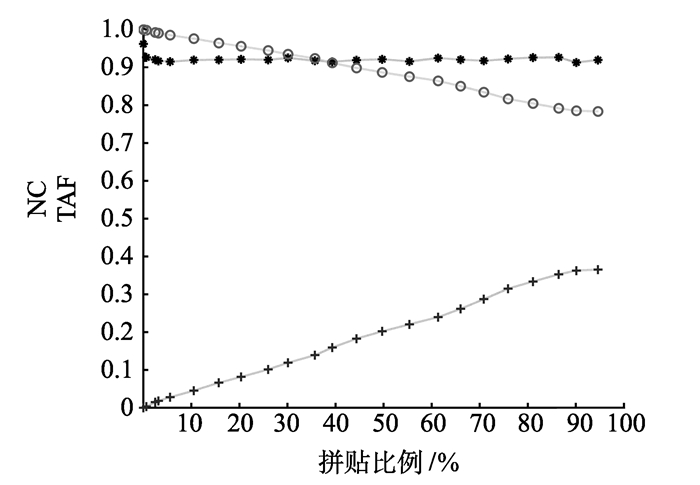
图 10 拼贴2攻击试验结果 Figure 10 Experimental results of the second collage attacks |
|
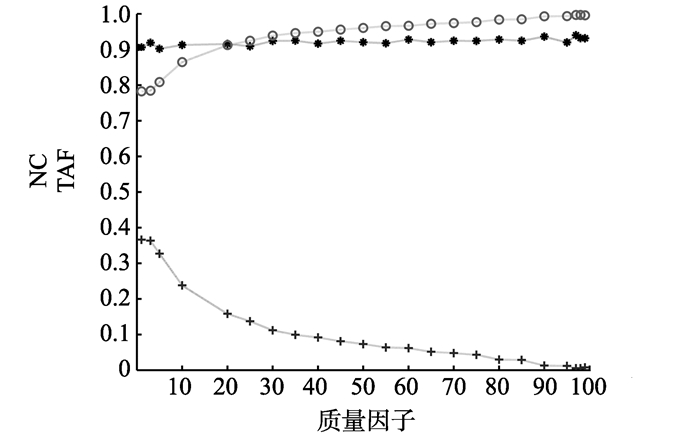
图 11 JPEG压缩攻击试验结果 Figure 11 Experimental results of the JPEG compressing attacks |
|
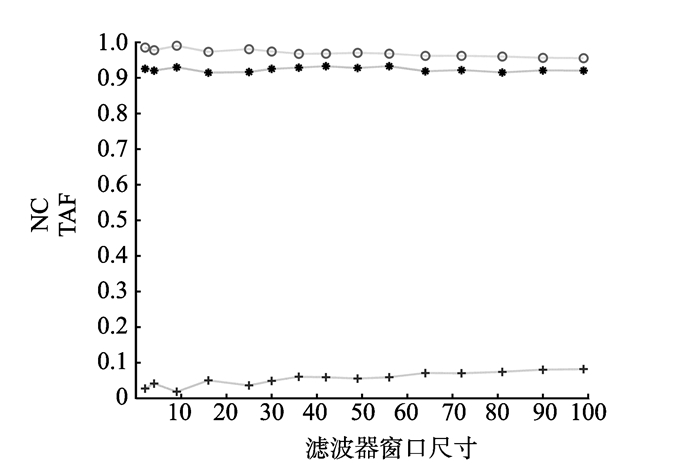
图 12 中值滤波攻击试验结果 Figure 12 Experimental results of the median filtering attacks |
|
图 13 高斯噪声攻击试验结果 Figure 13 Experimental results of the gaussian noise attacks |
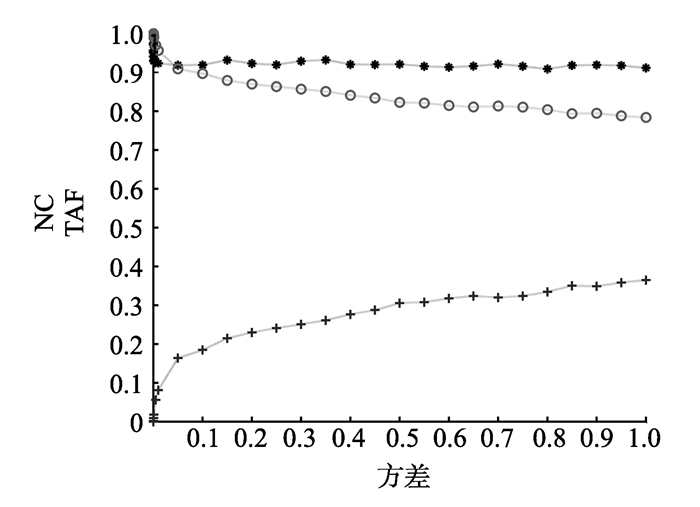
|
图 14 椒盐噪声攻击试验结果 Figure 14 Experimental results of the salt & pepper noise attacks |
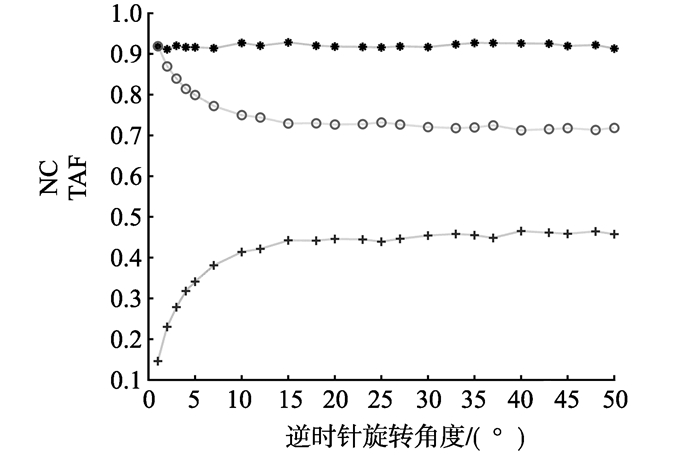
|
图 15 旋转攻击试验结果 Figure 15 Experimental results of the rotating attacks |
文献[21]提出了利用三层BP神经网络的数字图像零水印算法。所提出的算法使用的原始图像是512×512的Lena灰度图像, 算法中只嵌入了一种自制的32×32的二值水印图像。将二维水印图像进行混沌置乱, 再转换成一维数据。将宿主图像分成互不重叠的3*3子块, 根据密钥, 从宿主图像随机提取N个子块, 记录每个子块中心点像素值和平均像素, 建立N个子块到其平均像素的BP神经网络, 根据每个子块中心点像素值和BP神经网络输出之间的关系获取二值序列, 将此二值序列和混沌置乱后的一维水印数据进行异或运算得到构造出的二值零水印。受到攻击后, 本研究算法和文献[21]算法提取的水印图像的NC如表 1所示。
| 表 1 文献[21]和本研究算法水印NC比较 Table 1 Comparison of NC values of extracted watermarking images between the 21st reference and the diagram of this research |
由表 1可知, 在受到中值滤波、高斯噪声、质量因子为50的JPEG压缩后, 本研究算法提取出的鲁棒水印NC都大于文献[21]算法提取出的水印NC。在受到表 1所示的各种攻击后, 除椒盐噪声攻击, 本研究算法提取出的半脆弱水印NC都大于文献[21]算法提取出的水印NC。从整体看, 在受到表 1所示的各种攻击后, 本研究算法提取的鲁棒水印和半脆弱水印结合, 抵抗攻击的能力几乎都强于文献[21]算法的抗攻击能力。
文献[23]提出一种基于超混沌的医学图像篡改定位零水印算法。算法所用的原始图像是256×256的CT图像, 水印图像为256×256的二值图像。将原始图像最低有效位置零, 将原始图像分成不重叠的子块, 计算每个子块的平均值。根据子块每个像素值和子块平均值间的关系构成特征矩阵, 将特征矩阵进行Arnold置乱, 与超混沌加密的二值水印进行异或运算, 从而构造零水印。受到攻击后, 本研究算法和文献[23]算法提取的水印图像的NC如表 2所示。
| 表 2 文献[23]和本研究算法提取的水印图像NC比较 Table 2 Comparison of NC values of extracted watermarking image between the 23rd reference and the diagram of this research |
由表 2可知, 在受到表中的高斯噪声、椒盐噪声攻击时, 本研究算法提取的鲁棒水印和半脆弱水印NC都大于文献[23]算法提取的水印NC。在受到表 2中的剪切攻击后, 本研究算法提取的鲁棒水印和半脆弱水印NC略低于文献[23]算法提取的水印NC。
综合表 1、2中的试验结果, 与文献[21, 23]算法相比, 本研究算法抵抗各种攻击能力大多优于文献[21, 23]算法。
3.3 试验结果及分析试验结果可以看出, 本算法在原始图像未受攻击时, 提取的鲁棒和半脆弱水印图像的NC都能达到1;当受到攻击时, 鲁棒水印对剪切等攻击都有很好的抵抗能力。特别是由于采用了深度卷积网络, 能够构造体现原始图像关键特征的零鲁棒水印图像, 当攻击强度大时, 鲁棒水印图像的相似度NC还能达到90%以上, 能够很好地对原始图像进行版权保护。半脆弱水印对这些攻击能够较好地定位, 也能对原始图像进行版权保护。不足之处是, 在受到强度不太大的攻击时, 提取鲁棒水印的NC有时不能达到98%以上。但是, 鲁棒水印的这一不足, 可以由半脆弱水印来补充, 因为在攻击强度小时, 提取的半脆弱图像一般能保持98%以上的NC, 所以两种水印互补, 使得本算法的综合性能较好。
4 结论本研究提出一种基于SVD和DCNN的彩色图像多功能零水印算法。试验结果表明, 该算法在受到常见攻击后, 有较好的抗攻击能力, 半脆弱水印在原始图像受到剪切等攻击时定位良好, 特别是由于采用了DCNN, 鲁棒水印对强度大的攻击的抵抗能力优于一般算法。算法可以用于医学图像、毕业证、身份证等证书图像的保护中, 有较好的应用前景。
| [1] | TIRKEL A Z, RANKIN G A, SCHYNDEL R G, et al. Electronic watermark[C]//Digital Image Computing, Technology and Applications(DICTA), 1993. Sidney, Australia: Australian Pattern Recognition Society, 1993: 666-673. https://www.researchgate.net/publication/274958522_Electronic_Watermark |
| [2] | 孙圣和, 陆哲明, 牛夏牧, 等. 数字水印技术及应用[M]. 北京: 科学出版社, 2004. |
| [3] | AMIT M, NEELESH M. Adaptive lossless medical image watermarking algorithm based on DCT & DWT[J]. Procedia Computer Science, 2016, 78: 88-94 DOI:10.1016/j.procs.2016.02.015 |
| [4] |
张君捧, 张庆范, 杨红娟. 基于块特征和混沌序列的图像篡改检测与恢复[J].
山东大学学报(工学版), 2014, 44(6): 63-69 ZHANG Junpeng, ZHANG Qingfan, YANG Hongjuan. Images tamper detection and recovery based on block features and chaotic sequence[J]. Journal of Shandong University(Engineering Science), 2014, 44(6): 63-69 DOI:10.6040/j.issn.1672-3961.0.2014.098 |
| [5] |
王向阳, 杨红颖, 牛盼盼, 等. 基于四元数指数矩的鲁棒彩色图像水印算法[J].
计算机研究与发展, 2016, 53(3): 651-665 WANG Xiangyang, YANG Hongying, NIU Panpan, et al. Quaternion exponent moments based robust color image watermarking[J]. Journal of Computer Research and Development, 2016, 53(3): 651-665 DOI:10.7544/issn1000-1239.2016.20148177 |
| [6] | NGUYEN T S, CHANG C C, YANG X Q. A reversible image authentication scheme based on fragile watermarking in discrete wavelet transform domain[J]. International Journal of Electronics and Communications(AEU), 2016, 70(8): 1055-1061 DOI:10.1016/j.aeue.2016.05.003 |
| [7] | AMINI M, AHMAD M O, SWAMY M N S. Digital watermark extraction in wavelet domain using hidden Markov model[J]. Multimedia Tools and Applications, 2017, 76(3): 3731-3749 DOI:10.1007/s11042-016-3975-0 |
| [8] |
温泉, 孙锬锋, 王树勋. 零水印的概念与应用[J].
电子学报, 2003, 31(2): 214-216 WEN Quan, SUN Tanfeng, WANG Shuxun. Concept and application of zero-watermark[J]. Acta Electronica Sinica, 2003, 31(2): 214-216 |
| [9] | ZHOU Z Y. Digital video zero-watermarking algorithm based on contourlet transform[J]. Microcomputer Information, 2010, 26(35): 82-84 |
| [10] | CHEN X S, BU G L, LI H T, et al. A video zero-watermark algorithm based on the contourlet transform[C]//The 3rd International Conference on Multimedia Technology(ICMT), 2013. Paris, France: Atlantis Press, 2013: 216-223. https://www.researchgate.net/publication/266649111_A_Video_Zero-watermark_Algorithm_Based_on_the_Contourlet_Transform |
| [11] | CAI Y M, GUO W Q, DING H Y. An audio blind watermarking scheme based on DWT-SVD[J]. Journal of Software, 2013, 8(7): 1801-1808 |
| [12] | LEI M, YANG Y, LIU X M, et al. Audio zero-watermark scheme based on discrete cosine transform-discrete wavelet transform-singular value decomposition[J]. China Communications, 2016, 13(7): 117-121 DOI:10.1109/CC.2016.7559083 |
| [13] | ZHU P, XIANG G L, SONG W N, et al. A text zero-watermarking algorithm based on Chinese phonetic alphabets[J]. Wuhan University Journal of Natural Sciences, 2016, 21(4): 277-282 DOI:10.1007/s11859-016-1171-8 |
| [14] | JALIL Z, MIRZA A M, SABIR M. Content based zero-watermarking algorithm for authentication of text documents[J]. International Journal of Computer Science and Information Security, 2010, 7(2): 248-255 |
| [15] | KIM H D. CRT-based color image zero-watermarking on the DCT domain[J]. International Journal of Contents, 2015, 11(3): 39-46 DOI:10.5392/IJoC.2015.11.3.039 |
| [16] | SINGH A, RAGHUVANSHI N, DUTTA M K, et al. An SVD based zero watermarking scheme for authentication of medical images for tele-medicine applications[C]//The 39th International Conference on Telecommunications and Signal Processing(TSP), 2016. Vienna, Austria: IEEE, 2016: 511-514. http://ieeexplore.ieee.org/abstract/document/7760932/ |
| [17] | LE H D, XU X Y, WANG Q, et al. Zero-watermarking for face image protection in database[J]. Journal of Internet Technology, 2016, 17(1): 129-135 |
| [18] | VELLAISAMY S, RAMESH V. Inversion attack resilient zero-watermarking scheme for medical image authentication[J]. IET Image Processing, 2014, 8(12): 718-727 DOI:10.1049/iet-ipr.2013.0558 |
| [19] | HAN B R, LI J B, LI Y J. Zero-watermarking algorithm for medical volume data based on difference hashing[J]. International Journal of Computers Communications & Control, 2015, 10(2): 188-199 |
| [20] | LI D, LIU Z, CUI L H. A zero-watermark scheme for identification photos based on QR code and visual cryptography[J]. International Journal of Security and Its Applications, 2016, 10(1): 203-214 DOI:10.14257/ijsia |
| [21] |
倪顾伟. 基于神经网络的数字水印算法的研究与实现[D]. 南京: 南京理工大学, 2012.
NI Guwei. Research and implementation of digital watermarking algorithm based on neural network[D]. Nanjing: Nanjing University of Science and Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10288-1012320029.htm |
| [22] |
王雯霞. 一种基于奇异值分解的图像零水印新算法[J].
计算机时代, 2010(4): 8-10 WANG Wenxia. A new image zero-watermarking algorithm based on SVD[J]. Computer Era, 2010(4): 8-10 |
| [23] |
肖振久, 李南, 王永滨, 等. 基于超混沌的医学图像篡改定位零水印算法[J].
计算机工程与应用, 2017, 53(7): 115-120 XIAO Zhenjiu, LI Nan, WANG Yongbin, et al. Zero watermarking scheme for medical image temper location based on hyper-chaos encryption[J]. Computer Engineering and Applications, 2017, 53(7): 115-120 DOI:10.3778/j.issn.1002-8331.1510-0128 |
| [24] | LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324 DOI:10.1109/5.726791 |
| [25] | 谢剑斌, 兴军亮, 张立宁, 等. 视觉机器学习20讲[M]. 北京: 清华大学出版社, 2015. |




