2. 数字福建环境监测物联网实验室, 福建 福州 350117
2. Digit Fujian Internet-of-Things Laboratory of Environmental Monitoring, Fujian Normal University, Fuzhou 350117, Fujian, China
聚类分析作为数据挖掘的一种重要方法, 目的是将给定数据划分成多个子集(每个子集为一个簇), 使得簇内对象彼此相似, 与其他簇对象不相似[1]。目前聚类分析已广泛应用在Web搜索、图像处理、模式识别、医疗数据分析等众多领域。
传统的聚类算法可分为层次聚类、划分聚类、基于密度和网格聚类、其他聚类算法[2-5], 其中划分算法通过预先给定聚类数目和簇类代表点, 经反复迭代使目标函数收敛获得聚类划分[2]。传统聚类算法能较好处理常规数据(例如球形数据)。然而随着信息社会的发展, 数据越来越复杂, 例如医疗诊断数据, 不同簇之间样本数量和密度有较大差异, 这是典型的非均匀数据(通常也是类不平衡数据)。目前, 类不平衡数据的聚类分析是数据挖掘领域中的一个热点问题[6-7]。
K-means[8]是一种经典的聚类算法, 研究者将其引入到不平衡数据的聚类分析中, 但K-means算法在对类不平衡数据进行聚类时更倾向于形成大小相同的簇[9], 此为K-means算法的“均匀效应(uniform effect)[9]”。针对该问题研究者提出了多种方法, 可分为以下三类:聚类结果的评价[10]、数据预处理[11-12]、多代表点[13]。由于“均匀效应”的产生与K-means目标函数相关, 上述方法虽从不同角度给出了“均匀效应”的解决方法, 但并没直接从K-means目标函数角度解决“均匀效应”。
K-means目标函数为误差平方和, 误差平方和在形式上与方差相似, 而方差是度量数据离散程度的一种方式。K-means通过最小误差平方和, 使得簇中数据更紧凑, 同时使得簇中数据离散程度更低。变异系数作为数据离散程度的一种有效度量方式, 本研究提出以变异系数度量非均匀数据离散程度, 并以改进的变异系数为基础, 提出非均匀数据的相异度度量公式, 最后给出不同于K-means的划分型目标函数, 新的聚类算法为非均匀数据的变异系数聚类CVCN。
1 K-means聚类算法及“均匀效应”令给定的数据集DB={x1, x2, …, xi, …, xN}, 其中N为数据样本点数目; xi=[xi1 xi2 … xij … xiD]为一个D维的数据向量, 表示数据集DB的第i(i=1, 2, …, N)个样本点; xij为xi的第j维属性(j=1, 2, …, D)。典型硬聚类算法将DB划分成K个簇的集合C={c1, c2, …, ck, …, cK}, ck为DB的第k(k=1, 2, …, K)个簇, 且任意两个簇的交集为空集; μk=[μk1 μk2 … μkj … μkD]为一个D维向量, 表示第k簇的算术平均值, μkj为第k簇第j维的算术平均值。
经典K-means算法是一种划分型算法, 多以簇中数据的均值μk作为簇的代表, 通过度量样本与簇代表点μk的相异度定义目标函数
| $ \begin{array}{l} J\left( C \right) = \sum\limits_{k = 1}^K {\sum\limits_{{\mathit{\boldsymbol{x}}_i} \in {C_k}} {{{({\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{\mu }}_k})}^2}} }, \\ \;\;\;\;\;\;{\mathit{\boldsymbol{\mu }}_k} = \frac{1}{{\left| {{c_k}} \right|}}\sum\limits_{{\mathit{\boldsymbol{x}}_i} \in {C_k}} {{\mathit{\boldsymbol{x}}_i}} 。\end{array} $ |
由于K-means算法目标函数的优化是NP问题[14], 因此常用EM算法[15-16]进行优化。其算法简要过程为:首先给定初始簇数目、簇均值, 然后通过度量样本与不同簇原型点的距离, 将距离最小者划分到对应簇; 根据新划分的簇计算簇原型点; 算法迭代进行, 直到满足停止条件, 使得簇中样本与原型点距离的平方误差和取得局部最优值, 从而满足簇中数据更紧凑、簇间数据更分离的聚类划分目的。从数据分布角度, 簇中数据越紧凑, 表明簇中数据的离散程度越低。
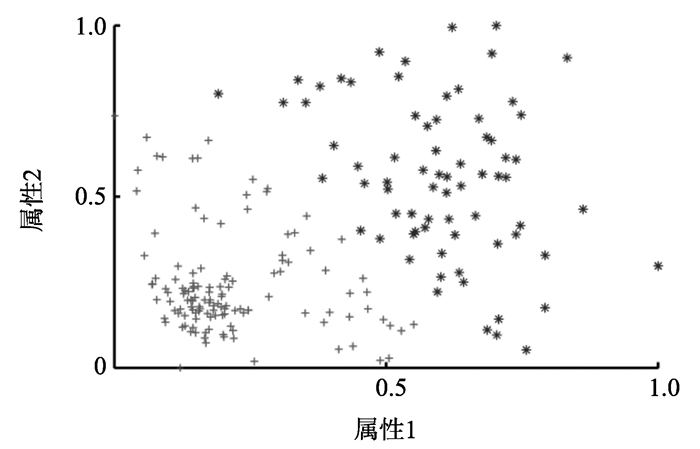
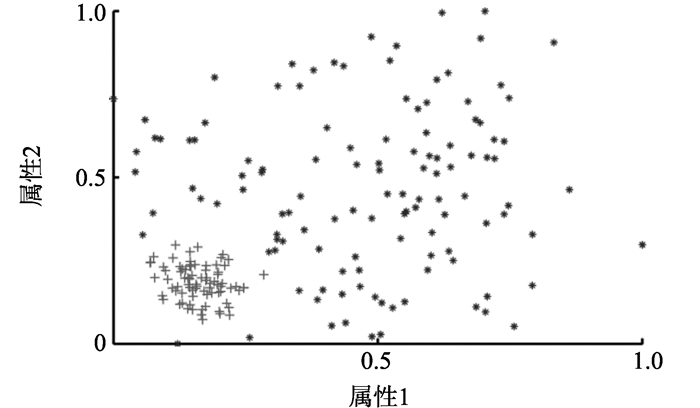
K-means型划分算法因算法结构简单、易实现且在常规数据集上有较高的时间效率和聚类精度等特点, 被广泛应用[17]。但不同数据集的特点不同, 如图 1中数据(进行了归一化处理)不同簇之间样本数目和密度有较大差异, 这是一种典型的非均匀数据。图 2为经典K-means算法对图 1数据聚类的结果, 图中两个簇的大小近似相同, 为K-means算法的“均匀效应”[9]。
|
图 1 一个二维非均匀数据的例子 Figure 1 An example of a two dimensional |
针对此问题, 研究者提出了不同方案, 可分为以下三类:(1)聚类结果评价, 文献[10]对外部准则进行标准化处理(即对外部准则公式进行相应标准化), 从而使其能反映聚类结果中“均匀效应”现象, 进而更准确度量聚类结果; (2)数据预处理, 在类不平衡数据处理中, 欠采样和过采样是两种应用较广泛的方法, 文献[11-12]分别将这两种方法引入到非均匀数据的预处理中, 通过将预处理后的数据与K-means结合给出聚类划分; (3)多代表点方法, 文献[13]提出用多个代表点表示类不平衡数据中的一个簇, 即对一个簇用多个划分子集表示, 最后将划分子集凝聚为簇。K-means目标函数为误差平方和, 图 1中, 类不平衡数据中主类为数据分布较分散的簇, 样本较少的类分布较集中, 这使得K-means算法度量样本与簇代表点之间相异度时, 多数类边缘样本更易被划入少数类中(如图 2所示), 少数类“吸收”主类样本产生“均匀效应”。
“均匀效应”与K-means目标函数相关, 而目标函数的优化在数据分布上体现数据离散程度的优化, 本研究从数据离散程度度量出发, 尝试用其他方式度量非均匀数据的离散程度, 以此角度解决“均匀效应”问题。
2 CVCN聚类算法 2.1 基于变异系数的相异度度量在统计学中, 均值、方差、标准差、变异系数均是度量样本变异程度(离散程度)的指标, 其中变异系数为标准差与均值的比值。通过引入均值, 消除度量数据离散程度时受不同水平均值影响[18], 定义式[19]
| $ {\rm{CV}} = \frac{\sigma }{\mu } = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{\mu }}_k})}^2}} } /\mu, $ | (1) |
式中:σ为总体样本(population)的标准差; μ为总体样本的均值; n为样本数量。因为非均匀数据不同簇之间的均值水平不同, 本研究以变异系数度量数据离散程度, 消除度量非均匀数据离散程度时受簇均值影响。同时本研究将变异系数引入到度量样本与簇相异度中, 提出一种非均匀数据的相异度度量公式
| $ {L_{\left( {{\mathit{\boldsymbol{x}}_i}, {c_k}} \right)}} = \sum\limits_{j = 1}^D {\frac{{{{\left( {{x_{ij}} - {\mu _{kj}}} \right)}^2}}}{{\mu _{kj}^2}}} ;{\rm{ }}{\mu _{kj}} = \frac{1}{{\left| {{c_k}} \right|}}\sum\limits_{{\mathit{\boldsymbol{x}}_i} \in {c_k}} {{x_{ij}}}, $ | (2) |
式(2)以簇中数据均值作为簇的代表, 分母为簇中数据均值。参考K-means目标函数, 本研究对式(1)进行平方处理, 且与式(2)相比式(1)并未引入n(即簇中数据数量|ck|), 本研究以此保留数据的不平衡状态。此外式(2)与Fisher准则[20]在函数形式和提出目的上是不同的。
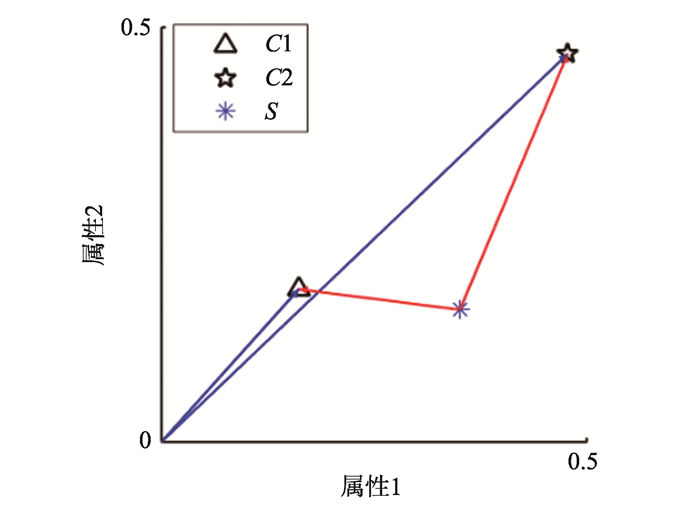
为了进一步解释本研究相异度公式度量样本点与不同簇之间的相异度, 本研究取图 1中点s进行说明, 并与传统基于欧氏距离的相异度度量公式进行了比较。图 3中蓝色向量为样本s与不同簇之间的欧氏距离, 红色向量为簇均值。
|
图 3 样本点s与不同簇的相异度 Figure 3 Dissimilarity between sample s and different clusters |
表 1为两种相异度公式的度量结果。经典K-means算法所用的基于欧氏距离相异度公式只需比较‖sc1‖2与‖sc2‖2, 表 1中‖sc1‖22<‖sc2‖22, 因此s将被划入第一个簇中; 根据本研究定义的相异度度量公式L(xi, ck), 由表 1可得L(s, c1)>L(s, c2), 则s将划入第二个簇中。而样本点s的类标签是第二簇, 说明式(1)能更准确地划分s点, 即该式能更好地刻画非均匀数据样本与簇的相异度。
| 表 1 样本s与不同簇(ck)的相异度度量结果 Table 1 Dissimilarity result between sample s and different clusters |
根据式(2)定义的相异度公式, 本研究以度量簇中样本整体相异度为基础, 给出非均匀数据的聚类优化目标函数如下:
| $ \begin{array}{l} \mathit{J}\left( C \right) = \sum\limits_{k = 1}^K {\sum\limits_{{\mathit{\boldsymbol{x}}_i} \in {c_k}} {\sum\limits_{j = 1}^D {\frac{{{{\left( {{x_{ij}} - {\mu _{kj}}} \right)}^2}}}{{\mu _{kj}^2}}, } } } \\ \;\;\;\;\;\;{\mu _{kj}} = \frac{1}{{\left| {{c_k}} \right|}}\sum\limits_{{\mathit{\boldsymbol{x}}_i} \in {c_k}} {{x_{ij}}} 。\\ \end{array} $ | (3) |
从优化角度分析, 划分型聚类算法是求解目标函数的最优值过程, 本研究以最小化式(3)为优化目标。由于式(3)定义在欧氏空间中, 而基于最小欧氏平方和的聚类是NP难问题[21], 此类问题较难求得最优值,
常通过优化算法获得局部最优值, 因此本研究采用迭代法求J的局部最优值。具体算法过程如下:
输入: 数据集DB, 簇数目K;
输出: 簇划分C。
(1) 初始化:随机生成初始簇代表点μkj, p=0;
(2) 更新C:利用式(2)度量样本与不同簇相异度, 将样本划入到相异度最小簇中;
(3) 更新μkj: if(μkj!=0)用式(3)更新μkj;
else: μkj=τ
(4) 迭代次数:p=p+1;
Until: ‖ μ(p)-μ(p-1)‖<ε
当簇代表点μ的两次迭代结果变化小于阈值ε时, 算法收敛获得局部最优解, 其中ε设为10-5; 当μkj=0时为了避免式(3)无意义, 将μkj设为极小值τ, 本研究τ取10-5。
2.3 算法分析从算法结构可知CVCN算法与K-means算法相似, 算法中每一步迭代过程的时间复杂度为O(KND), 假设算法迭代次数为P, 则CVCN算法时间复杂度为O(KNDP)。目标函数存在下限且算法每一次迭代过程中不提高函数值, 因此在有限迭代次后当目标函数不再改变时算法停止, 此时算法收敛局部最优值。
3 试验分析试验部分主要用来验证CVCN算法有效性。算法采用Java编写。试验平台如下:Core(TM)i5-3470 3.2 GHz CPU, 4 GB内存, 操作系统为Windows7。
3.1 试验设置试验选择了K-means、ESSC[22]、Verify2[23]3种算法进行对比。CVCN针对“均匀效应”定义了与经典划分型算法不同的离散程度度量方式, 为了检验新的离散程度度量方式在处理非均匀数据上效果, 本研究选择经典K-means。ESSC从簇内紧凑度和簇间分离性两个角度对数据进行聚类分析, 是K-means的一种代表性改进算法, 本研究选择ESSC, 验证此类K-means改进算法对非均匀数据的处理效果; 因为CVCN暂未考虑子空间问题, 为了试验公平性, ESSC未进行属性加权处理, 即wkj=1(k=1, 2, …, K; j=1, 2, …, D)。Verify2为文献[23]提出的一种将欠采样和谱聚类结合对类不平衡数据进行聚类分析的方法, 其中欠采样为类不平衡数据的一种代表性预处理方法。非均匀数据不同簇之间密度不同, 因密度算法对参数敏感, 本研究未将密度算法引入对比算法中。
合成数据能够从簇的数目、大小等控制数据集的簇结构, 便于分析算法的性能以及算法与簇结构之间的关系, 本研究首先在多个合成数据上进行测试, 然后在4个真实数据上试验。由于各数据集已知类标签, 本研究选择两个外部评价指标Macro-F1[24]和NMI[25]来评估新的算法聚类的性能, 两个指标的值越大表明聚类的效果越好。F(classk)第k个类的F-Measure, 计算公式为
| $ F\left( {{\rm{clas}}{{\rm{s}}_k}} \right) = \left( {\frac{{2 \times R\left( {{\rm{clas}}{{\rm{s}}_k}, {c_i}} \right) \times P\left( {{\rm{clas}}{{\rm{s}}_k}, {c_i}} \right)}}{{R\left( {{\rm{clas}}{{\rm{s}}_k}, {c_i}} \right) + P\left( {{\rm{clas}}{{\rm{s}}_k}, {c_i}} \right)}}} \right), $ |
式中:P(classk, ci)和R(classk, ci)分别表示数据集中真实的类classk与聚类结果中簇ci相比较的准确率和召回率; classk表示数据集中第k个真实的类; nk表示classk包含的样本点数。Macro-F1为所有类F-Measure和的算术平均值, 即
NMI即标准化互信息量(normalized mutual information)。其计算公式为
| $ {\rm{NMI}} = \frac{{\sum\limits_{i = 1}^R {\sum\limits_{j = 1}^K {{n_{ij}}{\rm{ln}}((N \times {n_{ij}})/({n_i} \times {n_j}))} } }}{{\sqrt {\sum\limits_{i = 1}^R {{n_i}{\rm{ln}}({n_i} \times N)} \times \sum\limits_{j = 1}^K {{n_j}{\rm{ln}}({n_i} \times N)} } }}, $ |
式中:nij表示真实数据集中类i与聚类结果中簇j相一致的样本点数目; ni表示属于类i的样本点数目; nj表示属于簇j的样本点数目; R表示真实类别数。
3.2 合成数据试验结果试验中利用Matlab合成DS1、DS2、DS3并进行了归一化处理,参数情况如表 2所示, 分布情况如图 1、4、5所示。本研究用标准差σ度量数据的分布情况, 计算公式为:
| $ \sigma = \sum\limits_{j = 1}^D {\sqrt {\frac{{\sum\limits_{{\mathit{\boldsymbol{x}}_i} \in {c_k}} {{{\left( {{x_{ij}} - {v_{kj}}} \right)}^2}} }}{{\left| {{c_k}} \right|}}} }, \left( {k = 1, 2, \cdots, K} \right)。$ |
| 表 2 合成数据集参数 Table 2 Parameters of synthetic datasets |
|
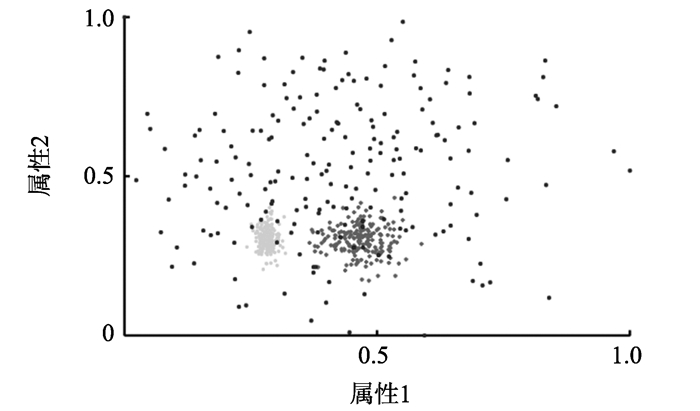
图 4 合成数据DS2 Figure 4 Synthetic data DS2 |
|
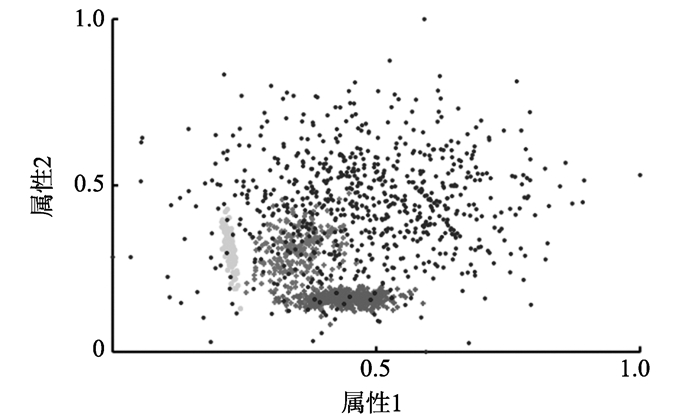
图 5 合成数据DS3 Figure 5 Synthetic data DS3 |
DS1有两个簇且簇中样本较小, 通过DS1测试CVCN算法在此类典型非均匀数据上表现; DS2为3个簇非均匀数据, 本研究通过DS2验证CVCN算法在簇样本数相同但有较大密度差异的此类数据上的表现; DS3为有4个簇的非均匀数据, 且此数据样本点数量较大, 通过DS3验证在多个交叠簇的非平衡数据上CVCN算法的表现。
根据上节分析, 这3种算法都是求局部最优解, 由于从不同的初始簇代表点出发导致的聚类结果不同, 因此试验中每个数据独立运行100次, 结果以“平均值±方差”形式表示。因为K-means、ESSC每次运行都需要选择初始簇代表点, 试验中2种算法运行时均采用相同的初始簇代表点。试验结果如表 3所示。对ESSC算法, 本研究选择了原文中一组参数, 因为ESSC对参数的要求使得其对不同数据的适应性降低, 同时ESSC是一种K-means型算法[26], 其相异度的度量方式依然是传统的欧氏距离, 表 3中ESSC在非均匀数据上聚类精度不高。表 3中CVCN算法在DS1、DS2、DS3的聚类精度与K-means、Verify2、ESSC相比有较大提升, 验证了合成数据集所设想的试验目的, 同时也表明本研究提出的相异度度量公式能较好地度量合成数据样本与簇之间相异度, 获得较高精度的簇划分。其中DS3是较复杂的数据, 其数据交叠严重且样本数量与DS1、DS2相比较大, CVCN算法在DS3上的试验结果明显优于对比算法。
| 表 3 合成数据集不同算法聚类结果 Table 3 Clustering results of different algorithms for synthetic datasets |
图 6显示了3种算法在合成数据上的运行时间。由于Verify2在算法设计中对主类样本进行多次欠采样并与谱聚类结合, 试验运行表明其耗时较长, 本研究未在图 6中给出。CVCN和K-means有相同的时间复杂度且两种算法初始条件相同, 图 6中K-means算法的运行时间较CVCN算法短, 表明K-means算法迭代次数比CVCN少, 即K-means算法受“均匀效应”影响会更快收敛形成大小相同簇, 而CVCN算法在本研究提出的相异度公式下, 以迭代次数增加为代价获得较高精度的簇划分。

|
图 6 合成数据不同算法运行时间对比 Figure 6 Comparison of the running time of different algorithms for synthetic data |
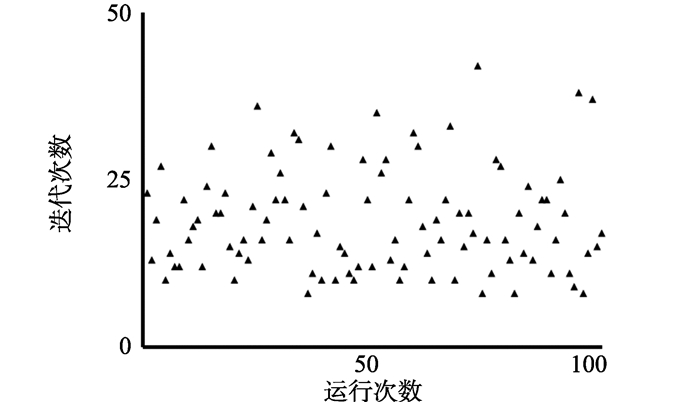
图 7为CVCN算法在合成数据集DS3上100次独立运行的迭代次数情况。可以看出CVCN算法在DS3上每次运行的迭代步骤是有限的, 从试验角度验证了算法在合成数据集上是收敛的。
|
图 7 DS3每次运行迭代次数 Figure 7 Iterations of DS3 every time |
真实数据来自聚类分析常用UCI Machine Learning epository(http://Archive.ics.uci.edu/ml/datasets.html)数据集。本研究选用了其中与生命科学相关(Life Science)的4个真实数据, 分别是Parkinsons、BreastCancer、ILPD、LSVT, 相关信息如表 4所示。
| 表 4 生命科学(life science)数据集相关信息 Table 4 Parameters of life science datasets |
其中Parkinsons为帕金森患者及正常患者语音数据, 患病者为主类; BreastCancer为疾病数据挖掘领域中常用的数据, 其中乳腺癌复发样本为少数类; ILPD为肝病数据, 其中患病样本为主类; LSVT为语言康复训练数据, 正确样本为主类。4个数据不同簇之间样本个数有较大差异, 是典型非均匀数据。CVCN及对比算法试验结果如表 5所示。
| 表 5 真实数据集不同算法聚类运行结果 Table 5 Clustering results of different algorithms of real datasets |
标准差可以从统计角度反映数据分布, 表 4中LSVT两个簇之间的标准差有较大差异, 而Parkinsons、BreastCancer、ILPD不同簇之间标准差差异较小。表 5中CVCN在LSVT上的聚类精度明显优于对比算法, 而在Parkinsons、BreastCancer、ILPD数据上CVCN优势不是很明显。综合CVCN在合成数据和真实数据上的试验结果, CVCN算法对簇大小和簇密度有较大差异的非均匀数据处理能力较强, 能一定程度解决“均匀效应”问题。
4 结论非均匀数据作为现实生活中一种常见的数据集, 簇的大小和密度存在较大差异, 变异系数可以较好地区分数据簇的上述差异。因此, CVCN算法提出以变异系数度量非均匀数据的离散程度, 并给出了一种非均匀数据的相似度度量方式, 进而给出了本研究的聚类目标函数。在部分实际数据集上的表现验证了本研究提出算法的有效性, 同时也表明算法有一定实用性。相较于当前非均匀数据的聚类算法, 本研究从非均匀数据离散程度直接切入是一种较为直接方法。
下一步的工作可分为两方面:一方面, 现实生活中存在类属型和混合属性的非均匀数据, 下一步尝试对这两类数据非均匀数据进行聚类分析; 另一方面, 目前高维数据的聚类分析是数据挖掘的一类难点问题, 非均匀数据中存在较多高维数据, 下一步对高维非均匀数据进行聚类分析。
| [1] | 韩家炜, 坎伯, 裴健. 数据挖掘: 概念与技术[M]. 3版. 范明, 孟小峰, 译. 北京: 机械工业出版社, 2012. |
| [2] | BERKHIN P. A survey of clustering data mining techniques[J]. Grouping Multidimensional Data, 2002, 43(1): 25-71 |
| [3] |
孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J].
软件学报, 2008, 19(1): 48-61 SUN Jigui, LIU Jie, ZHAO Lianyu. Clustering algorithms research[J]. Journal of Software, 2008, 19(1): 48-61 |
| [4] | JAIN A K, MURTY M N, FLYNN P J. Data clustering: a review[J]. Acm Computing Surveys, 1999, 31(3): 264-323 DOI:10.1145/331499.331504 |
| [5] | AGGARWAL C C, REDDY C K. Data clustering: algorithms and applications[M]. Boca Raton: CRC press, 2013. |
| [6] | HE H, GARCIA E A. Learning from imbalanced data[J]. IEEE Transactions on Knowledge & Data Engineering, 2009, 21(9): 1263-1284 |
| [7] | KRAWCZYK B. Learning from imbalanced data: open challenges and future directions[J]. Progress in Artificial Intelligence, 2016, 5(4): 1-12 |
| [8] | HARTIGAN J A, WONG M A. Algorithm as 136: a K-means clustering algorithm[J]. Journal of the Royal Statistical Society Series C:Applied Statistics, 1979, 28(1): 100-108 |
| [9] | XIONG H, WU J, CHEN J. K-means clustering versus validation measures: a data-distribution perspective[J]. IEEE Transactions on Systems, Man, and Cybernetics: Part B: Cybernetics, 2009, 39(2): 318-331 DOI:10.1109/TSMCB.2008.2004559 |
| [10] | WU J, XIONG H, CHEN J. Adapting the right measures for K-means clustering[C]//Proceedings of the the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris, France: ACM, 2009: 877-886. |
| [11] | KUMAR C N S, RAO K N, GOVARDHAN A. An empirical comparative study of novel clustering algorithms for class imbalance learning[C]//Proceedings of the Second International Conference on Computer and Communication Technologies(IC3T). Hyderabad, India: Springer India, 2016: 181-191. |
| [12] | KUMAR N S, RAO K N, GOVARDHAN A, et al. Undersampled K-means approach for handling imbalanced distributed data[J]. Progress in Artificial Intelligence, 2014, 3(1): 29-38 DOI:10.1007/s13748-014-0045-6 |
| [13] | LIANG J, BAI L, DANG C, et al. The K-means-type algorithms versus imbalanced data distributions[J]. IEEE Transactions on Fuzzy Systems, 2012, 20(4): 728-745 DOI:10.1109/TFUZZ.2011.2182354 |
| [14] | MAHAJAN M, NIMBHORKAR P, VARADARAJAN K. The planar K-means problem is NP-hard[J]. Theoretical Computer Science, 2009, 442(8): 274-285 |
| [15] | XU L, JORDAN M I. On convergence properties of the EM algorithm for Gaussian mixtures[J]. Neural Computation, 1996, 8(1): 129-151 DOI:10.1162/neco.1996.8.1.129 |
| [16] | MCLACHLAN G J, KRISHNAN T. The EM Algorithm and Extensions, Second Edition[M]. New York: [s. n. ], 2007. |
| [17] | JAIN A K. Data clustering: 50 years beyond K-means[J]. Pattern Recognition Letters, 2010, 31(8): 651-666 DOI:10.1016/j.patrec.2009.09.011 |
| [18] | BROWN C E. Applied multivariate statistics in geohydrology and related sciences[M]. Berlin: Springer, 1998. |
| [19] | EVERITT B. Cambridge dictionary of statistics[M]. Cambridge: Cambridge University Press, 2002. |
| [20] | 齐敏. 模式识别导论[M]. 北京: 清华大学出版社, 2009. |
| [21] | ALOISE D, DESHPANDE A, HANSEN P, et al. NP-hardness of Euclidean sum-of-squares clustering[J]. Machine Learning, 2009, 75(2): 245-248 DOI:10.1007/s10994-009-5103-0 |
| [22] | DENG Z H, CHOI K S, CHUNG F L, et al. Enhanced soft subspace clustering integrating within-cluster and between-cluster information[J]. Pattern Recognition, 2010, 43(3): 767-781 DOI:10.1016/j.patcog.2009.09.010 |
| [23] | LI X, CHEN Z, YANG F. Exploring of clustering algorithm on class-imbalanced data[C]//Proceedings of the 8th International Conference on Computer Science & Education (ICCSE). Columbo, Sri Lanka: IEEE, 2013: 89-93. |
| [24] | CHEN L, JIANG Q, WANG S. A probability model for projective clustering on high dimensional data[C]//Eighth IEEE International Conference on Data Mining. Pisa, Italy: IEEE Computer Society, 2008: 755-760. |
| [25] | STREHL A, GHOSH J. Cluster ensembles-a knowledge reuse framework for combining multiple partitions[J]. Journal of Machine Learning Research, 2002, 3(3): 583-617 |
| [26] | 陈黎飞, 吴涛. 数据挖掘中的特征约简[M]. 北京: 科学出版社, 2016. |