2. 电子科技大学计算机科学与工程学院, 四川 成都 610054
2. School of Computer Science and Engineering, University of Electronic Science and Technology of China, Chengdu 610054, Sichuan, China
压缩感知是一种新颖的信号处理理论, 在信号采样过程中直接丢弃掉不重要的信息成分, 仅仅对重要的信息分量进行采样, 这种方式能使压缩感知以远远低于Nyquist定理限定的采样频率对信号采样, 然后在解码端通过求解一个最优化问题将原始信号从少量的观测值中恢复出来[1-3]。压缩感知理论在无线传感器网络、超大带宽信号处理、雷达成像、遥感图像处理等等诸多领域内得到广泛的关注[4-5]。但是压缩感知重构算法存在计算量太大耗时较多、计算实时性太差的问题, 因此无法将压缩感知广泛应用[6-8]。如今, 并行计算的思想已经日趋成熟, 有多种实现并行计算的方式[9-10]。近年来兴起的图形处理器(graphics processing unit, GPU)采用简单控制逻辑, 大量晶体管用于算术逻辑计算, 在并行计算性能上带来很大的突破[11-15]。随着并行计算架构逐渐成熟, 科研人员将一些计算复杂度高、计算时间长的算法通过并行计算的方式进行加速[16-21]。文献[22]在对阈值迭代算法加速中, 通过对大规模向量相乘进行GPU加速, 将大部分的计算负担转移在支持集的选取中, 最后得到高达70倍的加速效果。文献[23]将压缩感知理论应用于超分辨率图像重构, 并采用GPU对其加速, 结果表明与串行计算相比得到100倍的加速效果。文献[24]采用GPU对压缩感知在高光谱图像中的应用进行加速, 利用模拟和真实数据进行试验, 揭示加速因子, 并在遥感高光谱数据压缩任务中取得良好加速效果。本研究针对CoSaMP在图像重构中计算时间过长的问题, 提出并行加速的方案, 并通过对图像重构进行测试试验, 试验结果与常规计算相比, 并行化方案得到50倍的加速效果, 极大的减少重构所需要的计算时间。
1 压缩感知压缩感知由3个部分组成:信号的稀疏表示、信号测量和信号重构。信号的重构是压缩感知的核心部分, 其作用是从测量数据中将原始信号恢复出来, 其原理为
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} x}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} \boldsymbol{\varPsi} a}}, $ | (1) |
式中: y为观测结果; Φ为测量矩阵; x为原始信号; Ψ为稀疏矩阵; a为稀疏信号。
由于该方程中未知数的数量要多于方程数量, 按照传统线性方程解法无法得到唯一解, 也就是说无法从该方程中精确的重构信号。但是由于信号x是稀疏的, 可以将上面的问题转换为求解l0范数的问题以较高的概率得到原始信号
| $ \mathit{\boldsymbol{a}} = {\rm{arg}}\;{\rm{min}}{\left\| \mathit{\boldsymbol{a}} \right\|_0}, \;\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\mathit{\boldsymbol{ \boldsymbol{\varPhi} \boldsymbol{\varPsi} a}} = \mathit{\boldsymbol{y}}, $ | (2) |
对式(2)进行求解, 研究人员提出两种解该方程的方法:基于求解最小l1范数的凸优化算法和基于求解最小l0范数的贪婪迭代算法。凸优化算法又包括基追踪匹配算法(basic pursuit, BP)、梯度投影算法(gradient projection for sparse, GP)等, 贪婪迭代算法包括匹配追踪算法(matching pursuit, MP)和在MP算法上改进得到的正交匹配追踪算法(orthogonal matching pursuit, OMP)、CoSaMP算法等等。由于CoSaMP算法相比其他算法具有鲁棒性好、计算相对简单而且计算精度相对高等特点, 选择该算法作为研究对象。
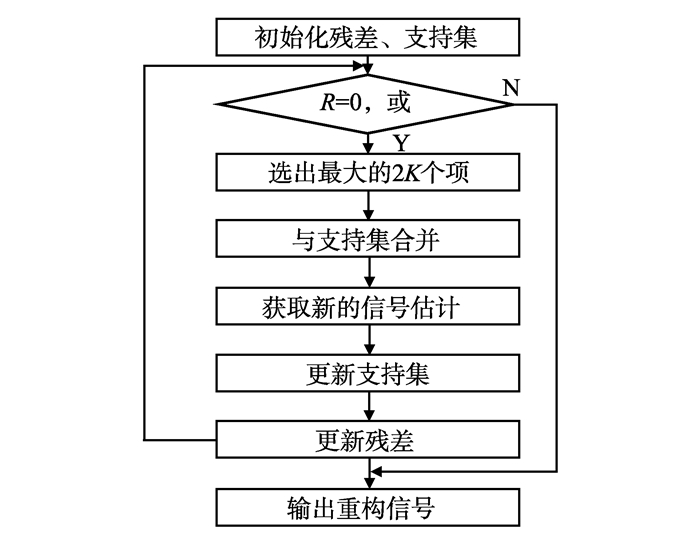
2 CoSaMP算法串行化实现为了验证CoSaMP算法的有效性, 本研究在图像重构过程中使用该算法做测试。对图像进行采样后再由重构算法处理, 通过对比原始图像和重构图像之间的性能来判断图像重构质量, 由此验证该算法的重构性能。在试验之前, 首先对该算法实现串行化, 再将测试用的图像读取到算法中进行处理。串行算法流程图见图 1。
|
图 1 CoSaMP算法流程图 Figure 1 Flowchart of the CoSaMP algorithm |
本试验的试验平台条件为主机采用Intel i5 5000处理器和4 GB内存容量, 测试用的图像为大小为512×512、1 024×1 024尺寸的灰度图像。由于CoSaMP算法的重构效果会受到信号长度N、测量维度M和稀疏度K较大的影响, 在该试验中, 选择多组不同参数作为对照组, 比较试验结果。
为了比较重构图像和原始图像之间的误差大小, 需要采用客观的数据来表示这个误差大小。本研究采用的是用峰值信噪比(peak signal noise ratio, PSNR)作为图像保真度系数, 其中
| $ {\rm{PSNR}} = 10{\rm{lg}}\frac{{{{255}^2}}}{{{\rm{MSE}}}}, $ | (3) |
式中:MSE为原始图像和遥感图像之间的均方误差。在试验过程中记录算法重构图像及其PSNR指数和算法执行的时间, 见表 1。
| 表 1 不同参数下重构算法的图像质量和时间 Table 1 Image quality and calculation time of the reconstruction algorithm at different parameters |
如图 2所示,随着测量度越高, 图像也更加的清晰, 稀疏度也会影响到图像最后的重构效果。同时从表 1中可以看出, 图像尺寸N和稀疏度K是影响算法执行时间的关键因素。随着图像尺寸或稀疏度的增加, 算法的执行时间也越来越高, 在尺寸为1 024×1 024, 稀疏度为0.1的时候, 重构时间为4 139 s。显而易见的是, 这种时间开销已经成为一个无法容忍的因素, 算法执行时间太长, 严重制约压缩感知技术的应用领域。因此, 为了压缩感知能更好的应用在各个行业中, 降低算法执行的时间开销迫在眉睫, 对算法的加速方案显得格外的重要。

|
图 2 重构图像与原始图像的对比 Figure 2 Comparison of the origin image with the reconstruction image |
在对CoSaMP算法进行GPU加速的时候, 首先要对串行化实现进行热点分析, 找出其中时间开销大并可以通过GPU进行加速的步骤, 找出制约算法性能的瓶颈。在使用时间库函数clock()计算出CoSaMP算法流程图中各个步骤的时间开销之后, 记录表明, 算法的主要时间开销在于最小二乘法计算过程中, 在以1 024×1 024图像做测试的时候, 这一个步骤的时间开销甚至达到整个重构过程的90%以上, 由于该部分的主要计算为矩阵操作, 而矩阵操作可以有效的通过并行化GPU对矩阵操作进行加速。
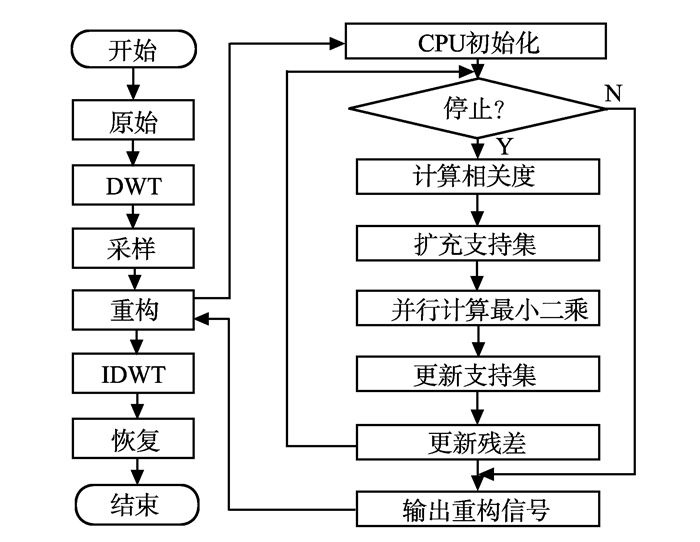
根据上面的分析, 该加速方案主要着重于将耗时多的矩阵操作从CPU端移植在GPU上进行计算, 在CUDA平台下编写矩阵操作的kernel函数代码实现加速,见图 3。
|
图 3 GPU并行化方案流程图 Figure 3 Flowchart of the parallel computing implement on GPU |
在加速过程中, CPU执行串行方案中的大部分代码, 当需要执行矩阵操作计算的时候, 调用矩阵加速代码, 将需要计算的数据从CPU发送到GPU端, 再执行kernel函数完成计算, 之后将计算结果从GPU端拷贝到CPU端完成加速。
为了检验该加速方案的有效性, 在实现加速方案代码后, 将代码在以下平台下作了试验测试:NVIDIA GTX 960, CUDA 8.0, Visual Studio 2013, Windows 7;本试验将采样率M/N设定为0.5, 根据图像尺寸和稀疏度大小, 采取了多个对照试验作比较, 并记录试验结果的重构质量和串行实现, GPU实现的时间, 用加速比来评价方案的加速效果。加速比
| $ {S_{\rm{p}}} = {t_{串行}}/{t_{并行}}, $ | (4) |
式中:t串行为串行方案的执行时间; t并行为并行加速方案的执行时间。
在试验过程中记录了重构算法执行的时间, 见表 2。
| 表 2 不同参数下的GPU并行方案的加速比 Table 2 Speed-up ratio of parallel computing on GPU at different parameters |
从表 2中可以看到, GPU加速方案在保证图像重构质量的情况下, 有效的加速算法的执行速度, 图像尺寸越大, 加速效果越好。与此同时, 试验结果也表明GPU加速方案的加速效果受到稀疏度K较大的影响, K越大, 加速效果越好。当图像尺寸达到2 048×2 048的时候, GPU加速方案对算法的加速比达到30倍, 将原来的重构时间从7 124 s下降到235 s, 取得不错的加速效果。
3.2 CoSaMP多线程加速方案针对CoSaMP重构算法在图像重构中的应用, 本研究提出使用CPU端的多线程技术, 对算法实现并行化加速。在图像重构过程中, 将整块的图像重构任务分割为n个不相关的计算任务, 在CPU上启动n个线程, 再将任务分配给n个线程分别实现重构计算, 每一个线程和其他的线程在计算过程中都保持独立性。利用CPU的多线程技术保持多个线程同时进行计算可以有效的提高算法的加速效果。
为了验证该方案的有效性, 针对CoSaMP算法在图像重构中在Intel(R) Xeon E5-2670的CPU硬件平台下进行试验, 通过对比单线程和多线程的执行速度来计算多线程加速方案的可行性。选取多个不同尺寸大小的图像, 测量比选定为0.5, 稀疏度为0.03, 进行多组对照试验并记录计算时间, 试验结果见表 3。
| 表 3 加速效果对比 Table 3 Comparison of the speed-up ratio |
由表 3可知, 多线程并行方案也有效的加速了算法的执行速度, 与串行方法相比, 加速的效果稳定的保持于6倍左右。在使用多线程进行加速时, 每个线程独立的负责一个任务计算, 由于在同一个时刻能稳定的保持一定数量的线程进行计算, 因此算法的加速保持稳定。
3.3 双重并行加速同时将CPU多线程技术和GPU加速两种并行化加速方案相结合提出新的加速方案——双重并行计算。在3.2节中提及到GPU和CPU之间的数据传输很大的影响到整体加速的效果, 当需要更高的加速效果的时候, 这种传输延迟已经成为制约加速效果的不可忽视的因素。同时在3.3节的多线程技术中说到, CPU的多线程机制有效的提供CPU的计算能力, 可以为开发者提供更多的线程保持同时计算。通常情况下, CUDA的编程模型为数据从CPU传输到GPU, 完成内核计算, 将计算结果从GPU传回到CPU端。这样, 在内核计算的时候, 便浪费了CPU和GPU的传输带宽; 同样在进行数据传输的时候, 也浪费了GPU的计算性能。在本方案中, 当一个线程在执行内核计算的时候, 其他线程可以完成数据的传输, 这样GPU总是能够保持内核计算和数据传输同时进行, 有效的提高计算性能。通过CPU端多线程并行和GPU的并行相结合的双重并行技术, 在保证CPU保持满载运算的同时, 可以有效的掩盖单线程GPU加速中CPU和GPU数据传输延迟造成的时间损耗。
在CPU+GPU异构计算平台下进行遥感图像重构试验。本试验选取硬件平台为CPU Intel i5-5 200U和NVIDIA GTX 960。选择多个不同尺寸的图像, 将采样率选定为M/N=0.5, 稀疏度K/N=0.03, 分别记录下每个试验中的该方案的执行时间, 分析该方案的加速效果。记录结果见表 4。
| 表 4 加速效果对比 Table 4 Comparison of speed-up ratio |
从表 4中可以看出, 本节并行加速的方案取得不错的加速效果。而且随着图像尺寸的增大, 加速的效果也得到明显的提升。在图像大小为2 048×2 048的时候, 与串行的重构算法相对比, 本节的加速效果达到54.68倍, 将重构时间从2 096 s下降到55 s, 可以满足人们对图像处理的实时要求。
4 结论(1) 将CoSaMP算法中计算比较耗时的矩阵操作部分移植到GPU异构计算平台上, 算法能够获得较好的加速效果。同时, 随着矩阵规模越大, GPU对算法的加速效果也越好。多线程对算法的加速效果比较平稳。
(2) GPU代码在执行过程中需要将数据从主机端和设备端之间拷贝, 当传输数据量较大的时候耗时较多, 会对加速效果有一定的影响。在主机端使用多线程技术, 以流水线的形式执行的时, 一个线程执行拷贝操作, 同时另一个线程执行核函数计算, 可以有效的掩盖数据传输带来的时延。
| [1] | DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306 DOI:10.1109/TIT.2006.871582 |
| [2] | LUSTING M, DONOHO D, PAULY J M. Sparse MRI: the application of compressed sensing for rapid MR imaging[J]. Magnetic Resonance in Medicine, 2007, 58(6): 1182-1195 DOI:10.1002/(ISSN)1522-2594 |
| [3] | FIGUEIREDO M A T, NOWAK R D, WRIGHT S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2008, 1(4): 586-597 |
| [4] | GHAHREMANI M, GHASSEMIAN H. Remote sensing image fusion using ripplet transform and compressed sensing[J]. IEEE Geoscience & Remote Sensing Letters, 2014, 12(3): 502-506 |
| [5] | WANG L, LU K, LIU P. Compressed sensing of a remote sensing image based on the priors of the reference image[J]. IEEE Geoscience & Remote Sensing Letters, 2015, 12(4): 736-740 |
| [6] | BLANCHARD J D, TANNER J. GPU accelerated greedy algorithms for compressed sensing[J]. Mathematical Programming Computation, 2013, 5(3): 267-304 DOI:10.1007/s12532-013-0056-5 |
| [7] | CHO M, MISHRA K V, XU W. Computable performance guarantees for compressed sensing matrices[J]. Eurasip Journal on Advances in Signal Processing, 2018, 2018(1): 16 DOI:10.1186/s13634-018-0535-y |
| [8] | KARAHANOGLU N B, ERDOGAN H. A*orthogonal matching pursuit: best-first search for compressed sensing signal recovery[J]. Digital Signal Processing, 2012, 22(4): 555-568 DOI:10.1016/j.dsp.2012.03.003 |
| [9] | ZHAO Y, YOSHIGOE K, BIAN J, et al. A distributed graph-parallel computing system with lightweight communication overhead[J]. IEEE Transactions on Big Data, 2017, 2(3): 204-218 |
| [10] | ASANOVIC K, BODIK R, DEMMEL J, et al. A view of the parallel computing landscape[J]. Communications of the Acm, 2009, 52(10): 56-67 DOI:10.1145/1562764 |
| [11] | GARLAND M, GRAND S L, NICKOLLS J, et al. Parallel computing experiences with CUDA[J]. Micro IEEE, 2008, 28(4): 13-27 DOI:10.1109/MM.2008.57 |
| [12] | SHI L, CHEN H, SUN J. VCUDA: GPU accelerated high performance computing in virtual machines[J]. IEEE Transactions on Computers, 2012, 61(6): 804-816 DOI:10.1109/TC.2011.112 |
| [13] | EGEL A, PATTELLI L, MAZZAMUTO G, et al. CELES: CUDA-accelerated simulation of electromagnetic scattering by large ensembles of spheres[J]. Journal of Quantitative Spectroscopy & Radiative Transfer, 2017, 199: 103-110 |
| [14] | JIANG H, GANESAN N. CUDAMPF: a multi-tiered parallel framework for accelerating protein sequence search in HMMER on CUDA-enabled GPU[J]. Bmc Bioinformatics, 2016, 17(1): 1-16 |
| [15] | GILBERT R, MIJAILOVICH S. Distributed multi-scale muscle simulation in a hybrid MPI-CUDA computational environment[J]. Simulation, 2016, 92(1): 19-31 DOI:10.1177/0037549715620299 |
| [16] | HANAPPE P, BEURIVÉ A, LAGUZET F, et al. Famous, faster: using parallel computing techniques to accelerate the FAMOUS/HadCM3 climate model with a focus on the radiative transfer algorithm[J]. Geoscientific Model Development Discussions, 2011, 4(3): 1273-1303 |
| [17] | MAROOSI A, MUNIYANDI R C, SUNDARARAJAN E, et al. Parallel and distributed computing models on a graphics processing unit to accelerate simulation of membrane systems[J]. Simulation Modelling Practice & Theory, 2014, 47(47): 60-78 |
| [18] | HUANG J W, ZHANG L Q, JIANG Z Y, et al. Heterogeneous parallel computing accelerated iterative subpixel digital image correlation[J]. Science China Technological Sciences, 2018, 61(1): 74-85 DOI:10.1007/s11431-017-9168-0 |
| [19] | ROMERO-LAORDEN D, VILLAZÓN-TERRAZAS J, MARTÍNEZ-GRAULLERA O, et al. Analysis of parallel computing strategies to accelerate ultrasound imaging processes[J]. IEEE Transactions on Parallel & Distributed Systems, 2016, 27(12): 3429-3440 |
| [20] | GUNARATHNE T, ZHANG B, WU T L, et al. Scalable parallel computing on clouds using Twister4Azure iterative MapReduce[J]. Future Generation Computer Systems, 2013, 29(4): 1035-1048 DOI:10.1016/j.future.2012.05.027 |
| [21] | LI S, FENG J. An optimized data processing model for computer big data platform based on parallel computing[J]. Boletin Tecnico/Technical Bulletin, 2017, 55(8): 318-324 |
| [22] | BLANCHARD J D, TANNER J. GPU accelerated greedy algorithms for compressed sensing[J]. Mathematical Programming Computation, 2013, 5(3): 267-304 DOI:10.1007/s12532-013-0056-5 |
| [23] | MOUSTAFA M, EBEID H M, HELMY A, et al. Rapid real-time generation of super-resolution hyperspectral images through compressive sensing and GPU[J]. International Journal of Remote Sensing, 2016, 37(18): 4201-4224 DOI:10.1080/01431161.2016.1209314 |
| [24] | BERNABÉ S, MARTÍN G, NASCIMENTO J M P, et al. Parallel hyperspectral coded aperture for compressive sensing on GPUs[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2016, 9(2): 932-944 |




