2. 中国民航大学天津市智能信号与图像处理重点实验室, 天津 300300
2. Tianjin Key Lab for Advanced Signal Processing, Civil Aviation University of China, Tianjin 300300, China
利用手指静脉特征进行身份识别是一种新兴的生物特征识别技术。手指静脉血管位于皮下, 无法表面成像。通常在透射模式下, 利用人体血管中脱氧血红蛋白对近红外光线的吸收特性, 通过图像传感器来获得血管网络图像[1]。因此, 手指静脉特征具有不易伪造、活体性强、友好便捷等突出优点。这些优势使手指静脉识别技术在生物特征识别领域得到了快速发展, 并逐步走向实际应用。
血管的网络结构是手指静脉特征的本质体现。因此, 提取图像的血管网络结构是实现手指静脉识别的关键。由于成像机制特殊, 手指静脉图像质量往往较差, 这为完整获取血管网络结构带来了很大困难。所以, 传统上大都以图像为基础, 借鉴其他生物特征(如指纹、人脸等)识别采用的特征分析和提取方法[2-6], 来解决手指静脉识别问题。
传统特征提取方法容易忽略图像特征的结构关系。图作为一种图像描述方式, 可以很好的描述图像区域之间的结构关系。本研究提出将图论和手指静脉识别结合在一起, 得到一个新的识别方法。构建手指静脉图像的加权图模型不仅能够描述全局的结构特征还能够通过边的权值来描述局部特征之间的关系。
图论最早的研究起源于瑞士数学家莱昂哈德欧拉, 他在1736年成功解决了哥尼斯堡七桥问题, 从而开创了图论, 在随后的200多年里, 图论逐渐发展, 由于其优异的特性, 如今已经广泛应用于运筹学、计算机科学等领域[7]。图论在图像聚类、模式识别方面都取得了较好的成绩。2003年, 罗斌等人[8]将图谱理论与图像聚类相结合, 实现了3D图像的聚类。2007年, 汤进等人[9]提出基于加权图谱特征的图像检索方法, 在不提高复杂度的前提下, 提高了基于内容的图像检索的精度。在2012年, Abusham和Bashir[10]将局部图结构(LGS)与人脸识别结合在一起, 减弱了光照对识别结果的影响。基于LGS, 董颂和杨巨成等人[11]在2015年提出基于多方向的加权局部图结构的手指静脉识别方法, 相比于传统方法, 该方法获得了更好的识别效果。因此将图论与手指静脉识别结合具有十分重要的研究价值。指静脉图像本身存在特殊性, 所以在确定图的顶点时既不能选取图像的像素点, 也不能采用细节点。因为图像中像素点过多, 会导致图的规模以及图的邻接矩阵维数过大, 静脉成像方法使得图像的细节点不稳定, 图像增强可能会产生虚假的细节点。顶点之间的连接关系构成加权图的边集。边集的选取和权值函数对加权图十分重要, 他们是对顶点之间某种关系的表达, 其中包括空间、颜色和纹理等关系, 边集和权值函数的选取不同, 图蕴含和表达的信息也是不同的。
本研究通过划分图块确定图的顶点, 划分图块不仅能对数据进行降维, 而且对图像平移的敏感性低, 提取的特征更加丰富。获得顶点集后, 构建三角剖分图, 然后根据权值函数对边赋权值, 获得加权图模型。
1 加权图对于手指静脉图像采用统一的图块划分方法, 获得的顶点集的空间分布是固定的, 只能通过边的权值来描述局部图像特征之间的关系。采用加权图更能够满足对于特征结构描述的需求。
加权图是由顶点集、边集和权值函数的三元关系集合组成的数据结构记为G(V, E, w), 其中V为顶点集, E为边集, w为权值函数[12]。设图G(V, E, w)的顶点集记为V={v1, v2, …, vn}, 其中n为顶点个数。图中任意一边记为(vi, vj)(i ≠ j), vi, vj为边连接的顶点。权值函数w对每一条边会赋一个非负实数wi, j, 当wi, j=wj, i时, 加权函数是对称的, 所得的加权图为无向图[12]。本研究采用的都是无向加权图。权值函数
| ${w_{i, j}} = {\rm{exp}}\left( {\left( { - \sum\limits_{l = 1}^m {{{\left( {{\mathit{\boldsymbol{\chi }}_i}\left( l \right) - {\mathit{\boldsymbol{\chi }}_j}\left( l \right)} \right)}^2}} } \right)/2{\sigma ^2}} \right), $ | (1) |
式中: χi、χj分别为顶点vi、vj的特征向量; m为特征的维数; σ为常数。关于顶点的特征描述在第2节中详细介绍。
1.1 顶点集的选取本研究采用均匀划分和滑窗划分两种图块划分方式, 如图 1所示。均匀划分是将图像均匀划分为一定大小的图块, 图块之间没有交叠部分; 滑窗划分是采用滑动窗口的方式划分图块, 图块之间存在交叠部分, 通过调节窗口滑动的步长, 可以调节交叠部分的大小。均匀划分是一种常用且高效的图块划分方式; 滑窗划分能够增加图块间的关联性, 进一步降低图块对平移的敏感度。

|
图 1 图块划分示意图 Figure 1 Rules of block division |
本研究依据三角剖分图确定边集, 将给定的顶点集连接成一个三角网。三角剖分图是一个较为简单、经典且鲁棒性较强的顶点连接方式, 其优点是单个顶点的变化主要影响局部的图结构, 对全局结构影响不大。由此可以确定式(1)中vi, vj之间的关系, 如图 2所示。

|
图 2 三角剖分图 Figure 2 Delaunay graph |
在本节中介绍了图的顶点与边集的选取方法, 构建加权图还需要确定边的权值, 由式(1)可知, 边的权值是由边所连接顶点的特征的相似度决定。因此还需要选取合适的顶点特征, 以及特征的提取方法。
2 特征提取采用方向可调滤波器(Steerable filter)提取图块的方向能量分布(oriented energy distribution, OED)作为顶点的特征。Steeral滤波器是图像处理的常用工具。方向可调滤波器是图像处理的常用工具, 1991年, Freeman和Aldson[13]首次通过一组具有不同方向的基础滤波器实现了一种方向可调的滤波器。在1996年, Simoncelli等人[14]利用希尔伯特变换对该方法进行了改进。
采用Steerable滤波器提取方向能量分布特征的原因为:首先, Steerable滤波器对图像中的曲线结构分析有着良好的性能。分析图块时, 主要考虑的是二值化图块中纹理曲线的结构特征, 并不考虑血管的粗细, 提取纹理的骨架也是为了消除血管粗细对特征的影响。其次, 图像进行二值化处理时, 当背景噪声过强, 在局部会出现点状虚假纹理。采用方向能量分布特征可以有效削弱这些影响, 方向能量分布特征对点状噪声纹理具有一定的鲁棒性。
特征提取步骤包括:首先将手指静脉图像进行二值化和细化处理, 其次将图像划分为图块, 最后利用Steerable滤波器对图块进行卷积, 获得图块的方向能量分布特征。
2.1 图像的二值化和细化方法提取方向能量特征需要对图像进行预处理, 包括二值化和细化, 对图像进行二值化能够消除大部分背景噪声对特征的影响, 对二值图像进行细化能够消除纹理粗细对特征的影响, 因为方向能量分布特征主要分析纹理曲线的分布和走向, 并不考虑纹理的粗细。二值化和细化过程包括:(1)利用去雾模型对图像进行复原, 去除图像中的散射现象[15]; (2)使用3尺度8通道的Gabor函数对图像进行滤波, 增强图像的血管区域[1, 16]; (3)采用多阈值算法对增强后的图像进行分割和二值化[17]; (4)对得到的二值图像进行细化处理, 采用文献[18]的细化算法。图像预处理各步骤的试验结果如图 3所示。

|
图 3 预处理结果 Figure 3 The preprocessing results |
Steerable滤波器的一般公式为:
| $ {h^\theta }\left( {x, y} \right) = \sum\limits_{j = 1}^N {{k_j}\left( \theta \right){f^{{\theta _j}}}\left( {x, y} \right)}, $ | (2) |
式中:k(θ)为内插函数; f(x, y)为任意滤波函数; θ为Steerable滤波器所在角度; θj为基础滤波器组中基础滤波器旋转的角度; N为基础滤波器的个数。方向能量分布特征为Steerable滤波器在0°~360°上滤波器响应的平方依序排列而得的向量, 方向能量在某一角度的计算公式为:
| $ E\left( \theta \right) = {\left( {{h^\theta }*{I_i}} \right)^2}, $ | (3) |
式中:hθ为Steerable滤波器; Ii是图像中第i个图块。将式(2)带入式(3)可得:
| $ E\left( \theta \right) = \left(\sum\limits_{j = 1}^N {\sum\limits_{x = 1}^X {\sum\limits_{y = 1}^Y {{{\left( {{k_j}\left( \theta \right)f{^{{\theta _j}}}\left( {x, y} \right){I_i}\left( {x, y} \right)} \right)}}} } }\right)^2, $ | (4) |
式中:X、Y为滤波器的尺寸, 与图块尺寸相同。式(4)能够计算单个方向上的纹理能量, 利用式(4)计算多个方向的纹理能量, 并合并为向量, 可得方向能量分布特征向量
| ${\mathit{\boldsymbol{\chi }}_i} = \left\{ {E\left( 1 \right), E\left( 2 \right), \cdots, E\left( \theta \right), \cdots, E\left( {360} \right)} \right\}。$ | (5) |
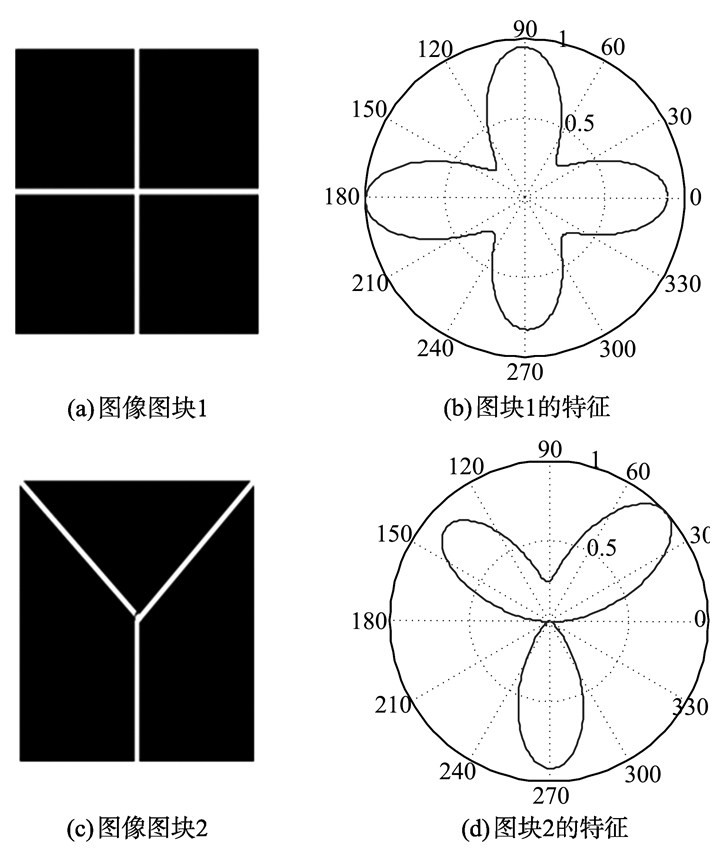
利用式(5)可计算图块的方向能量分布特征, 即顶点特征, 将不同顶点的特征向量带入式(1)就可以计算连接顶点的边的权值。图 4中给出了图块以及图块特征的示意图, 通过图 4可以看出方向能量分布特征能够较完整准确的描述图块中的纹理曲线结构。
|
图 4 不同图块的方向能量分布特征 Figure 4 The oriented energy distribution of different image blocks |
邻接矩阵表示图的各顶点之间关系的矩阵, 定义为AG是一个n×n的矩阵, n为顶点的数目, 其中它的行和列分别都表示图G的顶点, 当某两个顶点(vi, vj)之间有边连接, 则矩阵中对应的位置元素为1, 否则为0, 表示为:
| ${\mathit{\boldsymbol{A}}_G}\left( {i, j} \right) = \left\{ \begin{array}{l} 1, \;\;\;\;\;\;{\rm{if}}\left( {{v_i}, {v_j}} \right) \in E\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;{\rm{else}} \end{array} \right., $ | (6) |
将式(6)中“1”值改变为加权图中对应边的权值, 就可以得到加权图的邻接矩阵, 记为加权邻接矩阵Aw, 即:
| $ {\mathit{\boldsymbol{A}}_w}\left( {i, j} \right) = \left\{ {\begin{array}{*{20}{c}} {{w_{i, j}}, }&{{\rm{if}}\left( {{v_i}, {v_j}} \right) \in E}\\ {0, }&{{\rm{else}}} \end{array}} \right.。$ | (7) |
利用加权图的加权邻接矩阵, 可以将识别方法进一步简化, 将图的识别问题变为矩阵的相似性问题。本研究采用计算两个矩阵的相似度来判断两个图的相似性, 相似度
| $ S = \frac{{\sum\limits_p {\sum\limits_q {\left( {{A_{pq}} - \bar A} \right)\left( {{B_{pq}} - \bar B} \right)} } }}{{\sqrt {\left( {{{\sum\limits_p {\sum\limits_q {\left( {{A_{pq}} - \bar A} \right)} } }^2}} \right)\left( {\sum\limits_p {\sum\limits_q {{{\left( {{B_{pq}} - \bar B} \right)}^2}} } } \right)} }}, $ | (8) |
式中:p、q为矩阵的维数, p=q=n; A、B分别为矩阵A、B的均值。
4 试验及结果分析本研究试验分别是在两个图像库上进行的, 图库1为实验室采集的手指静脉图像库, 其中包含5 000张手指静脉图像, 共500类, 每一类包含10张图片, 将500类图片分为5组, 每组包含100类, 其采集图像与ROI图像如图 5所示; 另一个图像库是山东大学制作的公开手指静脉图像库, 库中一共有3 816张图像, 共有636类, 每类都有6张图片, 其采集图像和ROI图像如图 6所示。从该库中选取100类, 共600张图像, 并提取其ROI图像组成一个新的图像库记为图库2, 并用于试验测试。试验中, 采用留一法对所有图像都进行判别, 判别时将测试图像与所有训练图像进行相似度比对, 选取平均相似度最大的图像类别作为测试图像的类别。

|
图 5 图库1中原始指静脉图像及其ROI图像 Figure 5 Image of finger vein database 1 and its ROI image |

|
图 6 图库2中原始指静脉图像及其ROI图像 Figure 6 Image of finger vein database 2 and its ROI image |
在图库1的第一组图像中, 验证图块划分方式对于识别率的影响。选取图块的划分方式、图块的尺寸h以及滑窗划分图块的交叠部分尺寸k作为变量, 观察这些因素对识别结果的影响, 其中图块尺寸h和特征的刻画能力是一对相关联的因素。将试验分为两部分进行:(1)观察图块尺寸对识别结果的影响; (2)观察图块交叠尺寸对识别结果的影响。
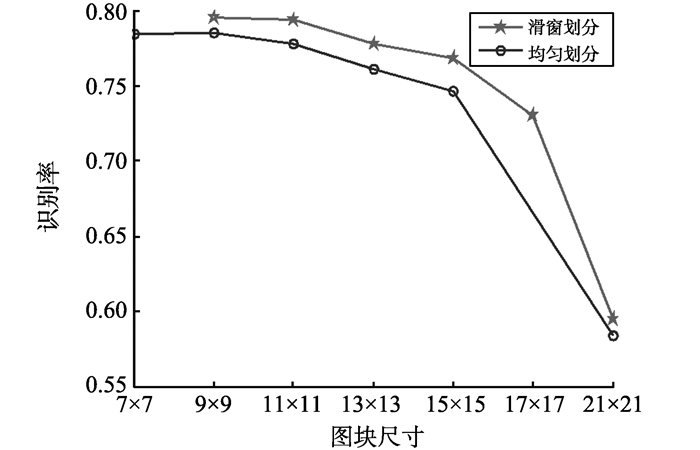
试验1中, 以图块尺寸h为变量, 观察均匀划分和滑窗划分方式下, 不同图块尺寸h对识别结果的影响, 其中图块尺寸h为奇数, 滑窗划分的交叠尺寸k=h/3, 试验结果如图 7所示。
|
图 7 两种图块划分方式在不同图块尺寸下的识别率 Figure 7 Recognition rate of two block divisions under different window sizes |
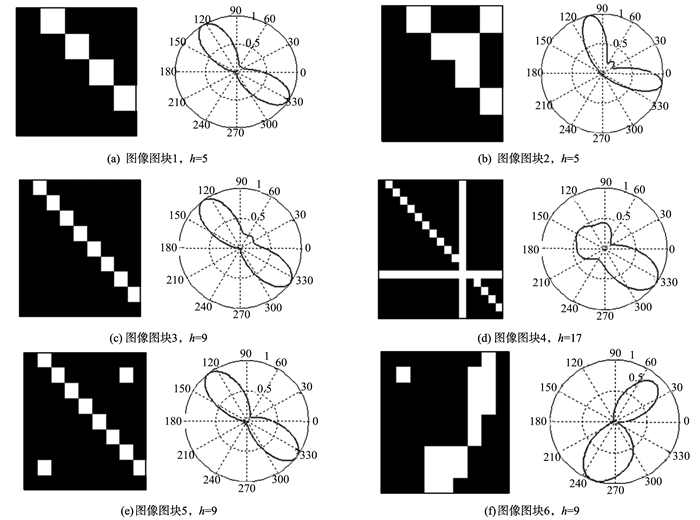
从图 7看出, 采用滑窗划分的方式, 可以获得更高的识别率; 随着图块尺寸减小, 识别率随之上升。图块之间存在重叠使得图块间的关联性得到了增强, 对于较小的位移有了更高的容忍度。结合不同尺寸的图块纹理以及图块特征进行分析, 如图 8所示, 可以发现当图块尺寸较小时, 图块的纹理相对单一, 图块之间的区分度较高, 这对识别是有利的, 如图 8(a)(d); 增大图块尺寸使得图块的纹理增多, 方向能量分布特征对纹理的刻画能力下降, 如图 8(c)(d), 影响图块特征区分度, 影响加权图对图像纹理的刻画。
|
图 8 不同尺寸图块的方向能量分布 Figure 8 Oriented energy distribution of blocks with different sizes |
通过观察图 8(a)(b)(c)发现, 随着图块尺寸减小, 图块中像素个数下降, 方向能量分布特征对不同尺寸图块中相似纹理的刻画存在局限性, 可能出错, 因此图块尺寸不应过小。从图 8(e)(f)可知, 图块的方向能量分布特征对边缘离散点状噪声的鲁棒性较强, 可以减弱二值化处理后残留的背景噪声对图识别性能的影响。
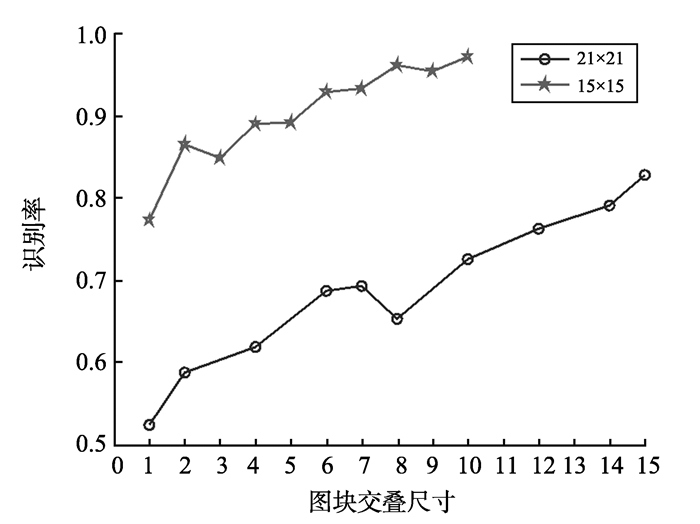
通过试验1可知, 通过滑窗划分构建加权图的顶点集, 能够提高加权图的识别性能。滑窗划分方式通过图块交叠来增加图块间的关联度, 用以提高特征描述的鲁棒性。滑窗划分中, 固定图块尺寸, 采用不同的图块交叠尺寸也会带来不同的图块划分结果, 因此试验2中主要讨论图块交叠尺寸对基于加权图的指静脉识别性能的影响, 分别通过识别精度和识别效率两方面进行分析, 结果如图 9、10所示。
|
图 9 滑窗划分方式在交叠大小不同时的识别率 Figure 9 Recognition rate of different overlap sizes |
|
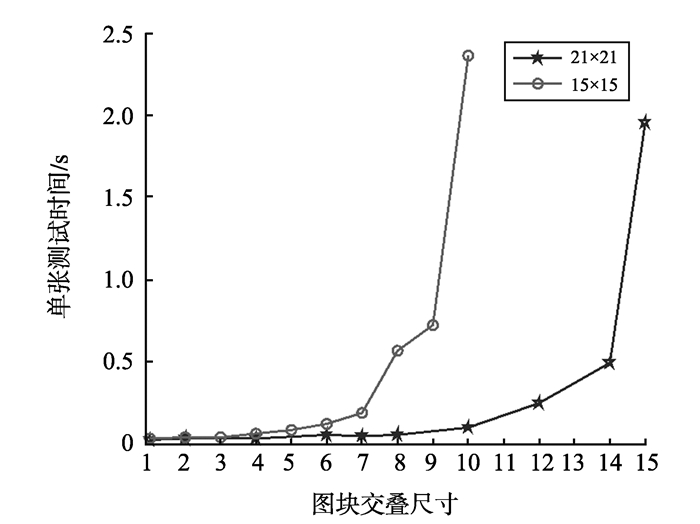
图 10 不同交叠尺寸下单张图像的测试时间 Figure 10 Single image test time of different overlap size |
从图 9、10可以看出, 随着滑窗的步长减小, 图块间的交叠尺寸增大, 识别率呈上升趋势; 与此同时, 单张图像的测试时间也随之上升, 当交叠部分超过图块尺寸的一半时, 测试时间急剧增加。增加图块的重叠部分, 效果近似于减小了图块的尺寸, 增加了加权图对局部特征的关注, 但是也增加了识别时的计算负担。通过观察图 9、10, 兼顾识别效率和识别精度, 图块的交叠尺寸应小于图块尺寸的一半, 因此本研究试验中图块交叠尺寸为图块尺寸的1/3。
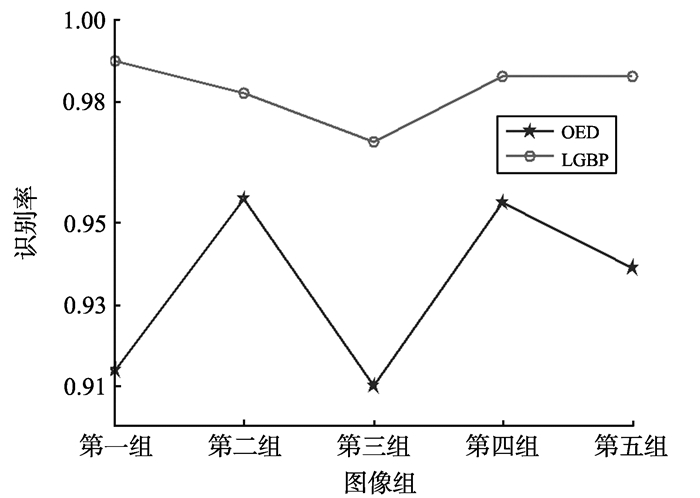
4.2 特征提取方法对识别率的影响特征提取是试验的关键部分之一, 不同的特征提取方法分析的局部特征不同。为了对比特征提取方法对识别率的影响, 选取LGBP特征[19]与方向能量分布特征作对比, 在图库1中进行试验, 对比试实验结果, 如图 11所示, 分别在图库1的5个图像组中对比两种不同特征提取方法的识别性能, 其中OED代表方向能量分布特征。
|
图 11 不同特征提取方法在图库上的识别率 Figure 11 Recognition rate of different feature extraction methods |
从图 11可以看出, 采用方向能量分布特征比LGBP特征在识别率上更具优势。因为LGBP仅描述中心像素与邻域像素之间的关系, 忽略了图块中纹理的结构关系, 而方向能量分布特征能够更好的刻画图块中的曲线结构, 包含着曲线的位置和走向等信息。
4.3 数据库识别结果为了验证本研究所提方法的普适性, 分别在图库1和图库2中进行对比试验。试验结果如表 1所示, 试验中对比两种图块划分方式在两个图库下的识别性能, 通过识别效率和识别精度进行评价。
| 表 1 不同数据库识别结果 Table 1 Recognition results of different databases |
由表 1可知, 本研究提出的方法在两个图库中都取得了较好的识别效果, 说明该方法具有一定的普适性。本研究方法在图库2中的识别率相对于图库1低, 分析原因为:图库2中每一个手指采集6张图片, 采集样本较少; 同类图像中存在较明显的姿态变化, 使得图像类内差异较大; 图像采集时存在漏光现象, 导致图像中光照不均匀, 影响图像的二值化结果的准确性。这说明本研究方向还需要进一步提高对光照和姿态变化的鲁棒性。
4.4 对比试验为了更好的评估本研究方法的性能, 将该方法与文献[20]提出的方法作对比。文献[20]将深度学习与手指静脉识别相结合, 利用神经网络对图像的血管区域进行分割, 根据分割结果进行识别。分别在两个数据库中试验这两种方法, 得到结果如表 2所示。
| 表 2 对比实验结果 Table 2 Compare experimental results |
从表 2可以看出, 对于两个数据库, 本研究方法在识别率上略低, 但是识别效率要远高于文献[20]中的方法。文献[20]中所采用的匹配方法具有精度高效率低的特点, 除此之外, 文献[20]对数据库具有较高的要求, 综合评价可得本研究方法具有较好的实用性。在后续工作中, 研究将致力于提高方法的识别精度。
5 结语本研究提出了一种基于加权图模型的手指静脉识别方法, 并对其进行详细说明。加权图通过对局部特征以及局部特征之间的关系, 来描述静脉血管网络结构。加权图能够较好的描述手指静脉网络结构, 试验证明该方法的有效性以及普适性。
但本研究仍存在一些问题:(1)本研究采用的图块划分方式, 没有参考图像的纹理分布, 这有可能造成了信息冗余和丢失; (2)本研究方法对图像的光照变化较为敏感; (3)式(1)存在参数σ, 需要进一步确定其对试验的影响, 并选取一个合适的值; (4)进一步提交识别精度。这些问题都需进一步研究。
| [1] | YANG Jinfeng, SHI Yihua. Finger-vein ROI localization and vein ridge enhancement[J]. Pattern Recognition Letters, 2012, 33(12): 1569-1579 DOI:10.1016/j.patrec.2012.04.018 |
| [2] | OJALA T, PIETIKAINEN M, HARWOOD D. A comparative study of texture measures with classification based on featured distributions[J]. Pattern recognition, 1996, 29(1): 51-59 DOI:10.1016/0031-3203(95)00067-4 |
| [3] | OJALA T, PIETIKAINEN M, MAENPAA T. Multi-resolution gray-scale and rotation invariant texture classification with local binary patterns[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2002, 24(7): 971-987 DOI:10.1109/TPAMI.2002.1017623 |
| [4] | ZHANG Lin, ZHANG Lei, ZHANG David, et al. Online finger-knuckle-print verification for personal authentication[J]. Pattern Recognition, 2010, 43(7): 2560-2571 DOI:10.1016/j.patcog.2010.01.020 |
| [5] | SUN Zhenan, TAN Tieniu. Ordinal measures for iris recognition[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2009, 31(12): 2211-2226 |
| [6] | CHAI Zhenhua, SUN Zhenan, VAZQUEZ H, et al. Gabor ordinal measures for face recognition[J]. IEEE Transactions on Information Forensics & Security, 2013, 9(1): 14-26 |
| [7] | WEST D. 图论导引[M]. 李建中, 骆吉洲, 译. 北京: 机械工业出版社, 2006. |
| [8] | LUO Bin, WILSON R, HANCOCK E. Spectral embedding of graphs[J]. Pattern Recognition, 2003, 36(10): 2213-2230 DOI:10.1016/S0031-3203(03)00084-0 |
| [9] |
汤进, 翟素兰, 罗斌. 基于加权关系图谱特征的图像检索[J].
计算机工程, 2007, 33(24): 19-21 TANG Jin, ZHAI Sulan, LUO Bin. Image retrieval based on graph spectra feature of attributed relational graph[J]. Computer Enginerring, 2007, 33(24): 19-21 |
| [10] | ABUSHAM E, BASHIR H. Face recognition using local graph structure (LGS)[J]. Lecture Notes in Computer Science, 2012, 6762: 169-175 |
| [11] | DONG Song, YANG Jucheng, CHEN Yarui, et al. Finger vein recognition based on multi-orientation weighted symmetric local graph structure[J]. Ksii Transactions on Internet & Information Systems, 2015, 9(10): 4126-4142 |
| [12] | UMEYAMA S. An eigendecomposition approach to weighted graph matching problems[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1988, 10(5): 695-703 |
| [13] | FREEMAN W, ADELSON E. The design and use of steerable filters[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1991, 13(9): 891-906 |
| [14] | SIMONCELLI E, FARID H. Steerable wedge filters for local orientation analysis[J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 1996, 5(9): 1377-82 DOI:10.1109/83.535851 |
| [15] | TAREL J, HAUTIERE N. Fast visibility restoration from a single color or gray level image[C]//Proceedings of International Conference on Computer Vision. Kyoto, Japan: IEEE, 2009: 2201-2208. |
| [16] | MOVELLAN J. Tutorial on Gabor filters[J]. Technical Report, 2002, 49: 1-23 |
| [17] | VLACHOS M, DERMATAS E. Vein segmentation in infrared images using compound enhancing and crisp clustering[M]. Heidelberg: Springer, 2008: 393-402. |
| [18] | YU Chengbo, QIN Huafeng, et al. Finger-vein image recognition combining modified Hausdorff distance with minutiae feature matching[J]. Interdisciplinary Sciences: Computational Life Sciences, 2009, 1(4): 280-289 DOI:10.1007/s12539-009-0046-5 |
| [19] |
张文超, 山世光, 张洪明, 等. 基于局部Gabor变化直方图序列的人脸描述与识别[J].
软件学报, 2006, 17(12): 2508-2517 ZHANG Wenchao, SHAN Shiguang, ZHANG Hongming, et al. Histogram sequence of local Gabor binary pattern for face description and identification[J]. Journal of Software, 2006, 17(12): 2508-2517 |
| [20] | QIN Huafeng, YACOUBI M. Deep representation-based feature extraction and recovering for finger-vein verification[J]. IEEE Transactions on Information Forensics & Security, 2017, 12(8): 1816-1829 |




