遥感图像的变化检测作为遥感图像分析中的一项重要应用, 广泛地应用于水资源环境监测、地理信息更新、城市规划等方面[1-2], 成为遥感图像处理领域中重要的研究内容。针对遥感图像的变化检测已经提出大量方法, 根据变化检测处理的基本单元级别可分为像元级[3-4]、特征级[5-6]和对象级[7]。基于多尺度分割技术的面向对象分析方法更符合图像中的实际地物分布, 能够充分利用地物的空间信息, 有效避免“椒盐效应”的产生, 受到学者们的青睐[8-9]。但现有的遥感图像变化检测方法存在许多问题, 不同时相的遥感图像因成像条件差异、水质变化以及植被物候变化等因素产生“伪变化信息”, 并且“同物异谱、同谱异物”现象也对水体周边环境变化检测造成干扰。本研究在光谱与纹理特征结合的基础上融合水体指数特征和植被指数特征创建针对水体周边环境变化检测的混合特征空间(spectrum texture ndwi savi, STWV), 针对混合特征空间中的遥感地物对象进行正反向异质性变化检测。首先采用超像素生成算法[10]处理两时相的叠加影像获取地物对象, 检查地物对象从时相1到时相2的Forward异质性, 再反向检测其从时相2到时相1的Backward异质性, 综合正反向的异质信息构建地物对象的正反向异质性, 然后使用最大数学期望(expectation maximization, EM)算法与贝叶斯最小错误率理论获取两时相的变化信息, 最后排除植被伪变化信息, 形成相对准确和鲁棒的变化检测结果。通过GF-1号PMS数据中石梁河水库周边环境的变化检测试验表明, 该方法能够有效区分水体周边环境中感兴趣的地物变化信息与不感兴趣的干扰信息、“伪变化信息”等, 从而提高水体周边环境的变化检测结果的精度。
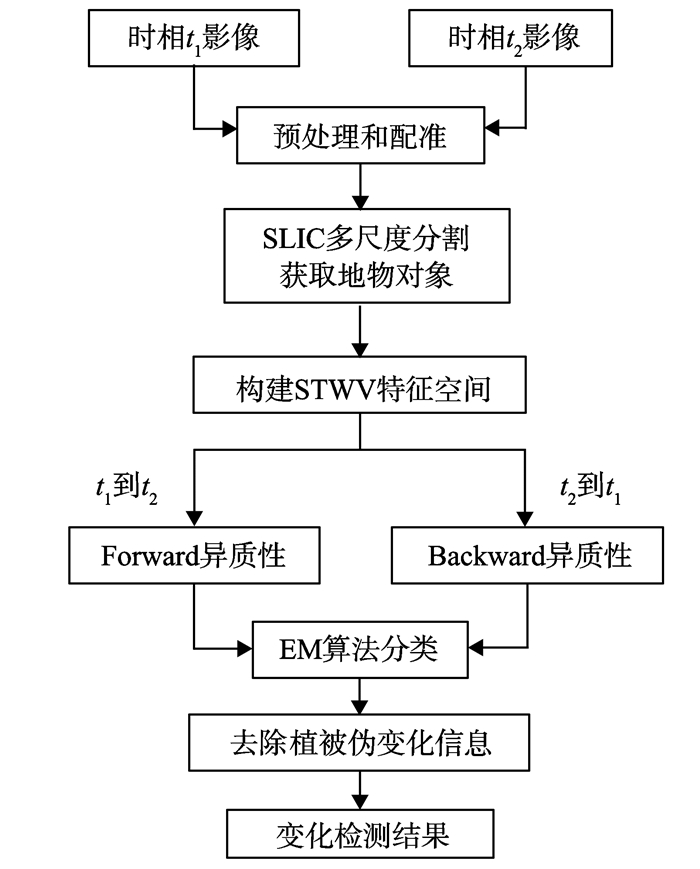
1 研究框架基于正反向异质性变化检测算法主要包括SLIC多尺度分割两时相叠加图像获取地物对象, 在混合特征空间中构建地物对象的正反向异质性, 通过EM算法对地物对象的异质信息进行分类和确定变化区域, 以及去除植被伪变化信息等步骤, 算法流程见图 1。
|
图 1 基于正反向异质性变化检测流程图 Figure 1 The flow chart of change detection based on Forward-Backward heterogenicity |
在面向对象的遥感图像变化检测方法中, 学者们通过多种图像分割算法获取地理对象, 如分形网络演化算法(fractal net evolution approach, FNEA)[11]、Mean-Shift分割算法[7]、分水岭分割算法[12]等。采用的简单线性迭代聚类算法SLIC是建立在K-means的思想基础上的多尺度分割算法, 能生成结构紧凑、色彩均匀的超像素, 在处理速度、物体轮廓保持以及分割效果等方面综合评价较高。
为获得两时相遥感图像中具有一致边界的地理对象, 通常将两时相遥感数据“叠合”为新图像, 然后对新图像进行多尺度分割。与传统的将两时相图像叠合为波段数两倍于原遥感图像的方案不同, 通过叠加的方式将两时相遥感图像中同一波段的数据等比例相加获得新的叠加图像, 叠加图像中包含了两时相遥感图像的地物分布信息, 然后通过SLIC算法对新图像进行多尺度分割, 再将分割结果套合在各时相遥感图像上以获取相应的地物对象。
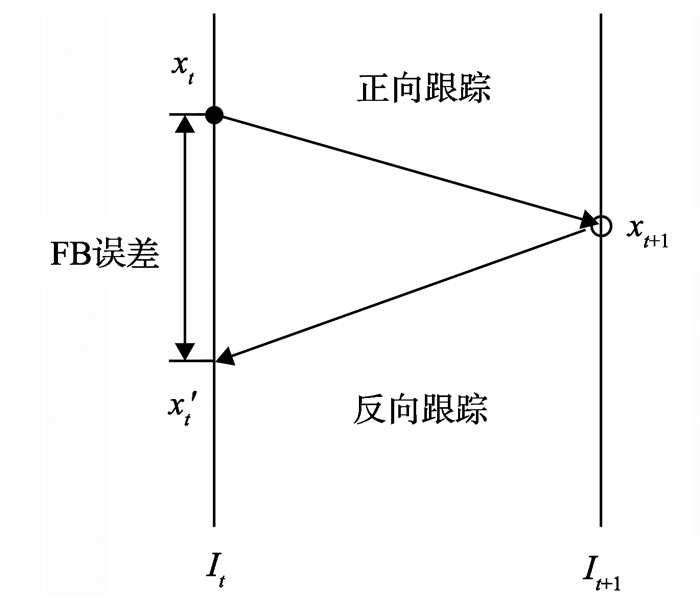
1.2 正反向异质性鲁棒的长时间单目标跟踪算法(tracking learning detection, TLD)[13]在其跟踪模块中使用中值光流法提出FB误差[14]的概念, 从t帧图像中前向跟踪一些点到t+1帧, 再反向跟踪回t帧, 然后计算反向跟踪回来的点与原始点位置之间的距离之差, 即认为目标跟踪的前向轨迹和后向轨迹应该是一致的, 如果两个轨迹存在误差, 记为FB误差。FB误差见图 2。
|
图 2 FB误差示意图 Figure 2 The sketch map of Forward-Backward Error |
TLD算法在跟踪器模块通过统计跟踪点的FB误差, 筛选出使跟踪器更稳定的特征点, 进而使得算法更稳定和鲁棒。在变化检测的应用场景中, 从时相1到时相2检测到的与反向检测到的变化信息应该是一致的, 区别只在于变化的方向是反向的, 但由于光照条件、传感器参数和太阳辐射角度等因素产生干扰信息的影响, 两时相图像的差异性并不都是变化信息。为减少遥感图像中的干扰信息和“伪变化信息”对水体周边环境变化检测造成的影响, 以地物对象的光谱、纹理、水体指数和植被指数等特征构造混合特征空间STWV。受TLD算法启发, 在混合特征空间中通过正向和反向计算两时相图像中地物对象的Forward异质性和Backward异质性来构建其FB异质性, 称之为正反向异质性, 然后利用正反向异质性进行变化检测。
1.2.1 混合特征空间在变化检测过程中只考虑地物对象的光谱特征这样的单一特征难以达到较高的精度, 融合多种特征构建更稳定和准确的变化检测模型是目前研究的热点方向。遥感图像变化检测的多特征融合方法通常考虑融合地物对象的光谱和纹理等特征[11], 对于变化检测中的干扰信息的处理有较好的效果。
在水体周边环境的变化检测问题中, 由于季节性的水质、植被等变化产生的“伪变化信息”等问题仍难以解决, 但这些“伪变化信息”的指数特征(水体指数、植被指数等)极为明显。基于局部二值模式(local binary pattern, LBP)[15]具有旋转不变性和灰度不变性等优点和归一化水体指数特征(normalized difference water index, NDWI)[16]在水体识别过程中具有的优秀表现以及土壤调节植被指数(soil-adjusted vegetation index, SAVI)[17]在植被类型识别中可以减小土壤背景影响的特点, 考虑融合地物对象的光谱特征、纹理特征LBP均匀模式和归一化水体指数NDWI、土壤调节植被指数SAVI来构建特征空间STWV。
1.2.2 Forward异质性从时相1到时相2图像通过距离相似度比较地物对象在混合特征空间中的特征相似度, 从而构建地物对象的Forward异质性。常用的距离相似度有绝对值距离、欧氏距离和卡方距离等, 其中绝对值距离和欧氏距离在多特征空间中各种特征信息为等权处理, 未能合理地体现出不同特征构造差异影像和表征变化信息的能力, 而卡方变换(chi square transformation, CST)可以根据两时相差值图像在不同特征上的方差, 综合考虑各种特征的权重值, 通过卡方变换构造的地物对象异质性更加客观和完整[18]。
为保证数据的一致性, 首先将混合多特征空间STWV中的各种特征归一化至[0, 1]范围内, 对于两时相遥感图像中的地物对象, 其内部像元的均值特征向量Vt={V1t, V2t, …, VQt}, t={1, 2}通过卡方变换计算第l个地物对象Forward异质性
| $ D_f^l = \sum\limits_{q = 1}^Q {\left( {\frac{{\mathit{\boldsymbol{V}}_q^2 - \mathit{\boldsymbol{V}}_q^1}}{{\sigma _q^{{\rm{diff}}}}}} \right)} , $ | (1) |
其中: σqdiff为两时相地物对象第q维特征差值的标准差, Q为特征维数值。
通过根据不同的地物对象作为样本计算特征差值的标准差可以反应图像中各地物对象在各维特征中的差异大小, 从而可以作为各维特征分布权重计算过程中的参考值。
1.2.3 Backward异质性Backward异质性是从时相2到时相1构建地物对象在混合特征空间中的异质性。分析地物对象的特征直方图可以发现, 尽管地物对象的内部像元特征分布不同, 但其表现特征却是一致的。考虑到计算Forward异质性时只考虑了地物对象的特征均值信息而未能考虑地物的特征分布信息, 可能导致漏检问题, 而地物对象的特征直方图不仅包含了地物的特征均值信息, 还包含了地物的特征分布信息[19], 因此考虑利用地物对象的特征直方图来构建其Backward异质性, 使得变化检测结果更为准确。
对数似然比统计量又称G统计量, 是一种非参数统计方法, 不需要对随机变量集合的分布情况预先作任何假设即可用于衡量两个随机变量集合之间的相似度, 使用G统计量衡量两时相地物对象在第q维特征上的直方图相似度(q=1, 2, …, Q), 计算式为
| $ \begin{array}{l} {G_q}\left( {{H_{t1}},{H_{t2}}} \right) = 2\left[ {\sum\limits_{{H_{t1}},{H_{t2}}} {\sum\limits_{i = 0}^{L - 1} {\left( {f_i^q\ln f_i^q} \right)} } - \sum\limits_{{H_{t1}},{H_{t2}}} {\left( {\sum\limits_{i = 0}^{L - 1} {f_i^q} } \right)\ln \left( {\sum\limits_{i = 0}^{L - 1} {f_i^q} } \right)} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\sum\limits_{i = 0}^{L - 1} {\left( {\sum\limits_{{H_{t1}},{H_{t2}}} {f_i^q} } \right)\ln \left( {\sum\limits_{{H_{t1}},{H_{t2}}} {f_i^q} } \right)} + \left( {\sum\limits_{{H_{t1}},{H_{t2}}} {\sum\limits_{i = 0}^{L - 1} {f_i^q} } } \right)\ln \left( {\sum\limits_{{H_{t1}},{H_{t2}}} {\sum\limits_{i = 0}^{L - 1} {f_i^q} } } \right)} \right], \end{array} $ | (2) |
其中:Ht1和Ht2为两时相遥感图像地物对象的特征直方图, fq为地物对象的第q维特征概率密度函数, L为该特征的量化等级。
对于单个地物对象来说, 其直方图累积概率值为1, 则有
| $ \sum\limits_{{H_{t1}},{H_{t2}}} {\left( {\sum\limits_{i = 0}^{L - 1} {{f^q}} } \right)\ln \left( {\sum\limits_{i = 0}^{L - 1} {{f^q}} } \right)} = 1\ln 1 + 1\ln 1 = 0, $ | (3) |
| $ \left( {\sum\limits_{{H_{t1}},{H_{t2}}} {\sum\limits_{i = 0}^{L - 1} {f_i^q} } } \right)\ln \left( {\sum\limits_{{H_{t1}},{H_{t2}}} {\sum\limits_{i = 0}^{L - 1} {f_i^q} } } \right) = 2\ln 2, $ | (4) |
则式(3)(4)化为
| $ {G_q}\left( {{H_{t1}},{H_{t2}}} \right) = 2\left\{ {\sum\limits_{{H_{t1}},{H_{t2}}} {\sum\limits_{i = 0}^{L - 1} {\left( {f_i^q\ln f_i^q} \right)} } - \sum\limits_{i = 0}^{L - 1} {\left( {\sum\limits_{{H_{t1}},{H_{t2}}} {f_i^q} } \right)\ln \left( {\sum\limits_{{H_{t1}},{H_{t2}}} {f_i^q} } \right)} + 2\ln 2} \right\}。$ | (5) |
为充分利用所有特征包含的信息, 在混合多特征空间STWV中计算第l个地物对象各特征维度的特征直方图相似度的加权平均值作为其Backward异质性
| $ D_b^l = \sum\limits_{q = 1}^Q {{\omega _q}{G_q}\left( {{H_{t1}},{H_{t2}}} \right)} , $ | (6) |
式中: ωq=E(q)/
在混合多特征空间STWV中计算得到第l个地物对象的Forward异质性Dfl和Backward异质性Dbl后, 即可得到该地物对象的正反向异质性Dfbl={Dfl, Dbl}。
1.3 变化信息检测 1.3.1 EM算法分类在使用SLIC算法多尺度分割两时相叠合影像获取遥感图像中的地物对象后, 计算地物对象的正反向异质性组合D={Dfb1, Dfb2, …, Dfbn}, 其中n为地物对象的个数。
在两时相遥感图像中, 发生变化的地物对象的异质性较大而未发生变化的地物对象异质性较小, 则D中的元素可分为变化和未变化两大类。假设D满足由两个高斯分量组成的混合高斯分布(gaussian mixture model, GMM), 其密度函数可表示为
| $ f\left( {D_{fb}^i} \right) = p\left( {D_{fb}^i\left| {{l_u}} \right.} \right)p\left( {{l_u}} \right) + p\left( {D_{fb}^i\left| {{l_c}} \right.} \right)p\left( {{l_c}} \right),i = 1,2, \cdots ,n, $ | (7) |
式中: lc和lu是变化类别和未变化类别标签, 记为l∈{lc, lu}; p(l)是l类元素在D中所占的比例, 满足p(lc)+p(lu)=1; p(Dfbi|l)为概率密度函数, 服从高斯分布
| $ p\left( {D_{fb}^i\left| l \right.} \right) = \frac{1}{{{\sigma _l}\sqrt {2{\rm{ \mathsf{ π} }}} }}\exp \left( { - \frac{{{{\left( {D_{fb}^i - {\mu _l}} \right)}^2}}}{{2\sigma _l^2}}} \right)。$ | (8) |
EM算法是一种求解概率模型参数的最大似然估计方法, 上述假设中的混合高斯分布模型的参数p(l)和均值μl、标准差σl可以用EM算法来估计[20]。
用K-means算法将D聚为两类, 进行迭代更新, 直至收敛。迭代模式为
| $ {p^{k + 1}}\left( l \right) = \frac{{\sum\limits_{i = 1}^n {{p^k}\left( {l\left| {D_{fb}^i} \right.} \right)} }}{n},\mu _l^{k + 1} = \frac{{\sum\limits_{i = 1}^n {D_{fb}^i{p^k}\left( {l\left| {D_{fb}^i} \right.} \right)} }}{{\sum\limits_{i = 1}^n {{p^k}\left( {l\left| {D_{fb}^i} \right.} \right)} }},\sigma _l^{k + 1} = \frac{{\sum\limits_{i = 1}^n {{p^k}\left( {l\left| {D_{fb}^i} \right.} \right)\left( {D_{fb}^i - \mu _l^k} \right){{\left( {\mathit{\boldsymbol{D}}_{fb}^i - \mu _l^k} \right)}^{\rm{T}}}} }}{{\sum\limits_{i = 1}^n {{p^k}\left( {l\left| {D_{fb}^i} \right.} \right)} }}。$ | (9) |
通过贝叶斯公式计算Dfbi属于类别l的后验概率
| $ p\left( {l\left| {D_{fb}^i} \right.} \right) = \frac{{p\left( {D_{fb}^i\left| l \right.} \right)p\left( l \right)}}{{p\left( {D_{fb}^i} \right)}}, $ | (10) |
根据最小错误率原则为Dfbi分配类别标签lc或lu, 获得对应地物对象的变化信息。
1.3.2 植被伪变化去除在水体周边环境的变化检测问题研究过程中, 只有地物类型发生变化的真实变化属于感兴趣的变化信息。由于季节、气候等原因, 同一植被覆盖区域(尤其是农田区域)在不同时相的植被特征可能发生改变, 产生“伪变化信息”, 属于不感兴趣的变化信息[21]。
基于植被覆盖度去除植被伪变化信息, 通过归一化植被指数计算不同时相像元的植被覆盖度, 然后估算变化类地物对象中植被像元的比例, 将两时相地物对象中植被像元比例都较高者, 认为该地物对象变化是因植被的季相变化引起的, 属于植被伪变化信息, 具体步骤如下:
(1) 计算像元i的植被覆盖度
| $ {F_c} = \left( {{N_{{\rm{DV}}{{\rm{I}}_i}}} - {N_{{\rm{DV}}{{\rm{I}}_{\min }}}}} \right)/\left( {{N_{{\rm{DV}}{{\rm{I}}_{\max }}}} - {N_{{\rm{DV}}{{\rm{I}}_{\min }}}}} \right), $ | (11) |
其中: NDVImin为遥感图像中像元的最小值, NDVImax为最大值。
(2) 计算变化对象中植被像元的比例
| $ {N_f} = \sum\limits_{x = 1}^n {\frac{{f\left( {{F_c}\left( x \right)} \right)}}{n}} , $ | (12) |
其中:
(3) 如果变化对象对应的两个时相的地物对象中, 植被像元的比例Nf都较高, 则认为该变化对象由植被物候变化而引起的伪变化。
2 试验结果与分析试验数据为中国卫星资源应用中心提供的石梁河水库周边区域(位于江苏省东北部)2015-04和2016-04的Level 1A级GF-1号PMS遥感图像, 包括空间分辨率为2 m的全色数据和8 m的多光谱数据, 经过ENVI5.1预处理和基于GS变换的图像融合重采样后, 融合图像(光谱范围是0.45~0.89 μm)的空间分辨率为2 m。水库周边环境复杂, 地物类型多样, 干扰信息以及“伪变化信息”等因素对变化检测结果影响较大, 本章选取3组该区域的数据进行试验来综合评价方法的有效性。
2.1 试验数据图 3中, 第一列试验数据是时相1即2015-04-18的图像, 第二列试验数据是时相2即2016-04-21的图像, 图 3(a)(b)图像的大小是1 166像素×881像素, 图 3(c)(d)图像的大小为747像素×564像素,图 3(c)(f)图像大小为597像素×452像素, 试验区域的变化信息主要包括水坝、房屋、水田等地物兴建和改造, 以及农田、森林等植被覆盖区域的物候变化和水质变化等“伪变化”。

|
图 3 3组不同区域的试验数据 Figure 3 Experimental data in three different regions |
试验数据中包含一些由于成像条件不同、光照变化等因素造成的干扰信息, 如图 4是试验数据1和试验数据3中干扰区域的局部放大图对比, 地物类型分别是裸地与建筑物。

|
图 4 试验区域的干扰信息 Figure 4 Interference information in the experimental area |
试验区域中的伪变化信息对水体周边环境变化检测结果影响巨大, 图 5是3组试验数据中典型的伪变化信息, 包括水坝区域的亮度伪变化、水质变化和植被物候变化等。

|
图 5 试验区域的伪变化信息 Figure 5 Pseudo change information in the experimental area |
试验数据1和数据2在包含水库边界人工水坝的修建和改造等变化信息的同时, 也包含因水位波动等原因导致的水田等区域的变化信息, 伪变化信息主要来源于水库水体本身水质变化与水坝区域的亮度变化; 数据3的主要变化信息是土地利用信息的改变, 包括房屋和水田的修建, 而植被的物候变化和水质变化是其主要的伪变化信息来源。
2.2.1 变化检测结果对比为验证本研究算法的有效性, 采用多种算法对试验数据进行变化检测:图 6~8是几种算法对3组试验数据分别进行多尺度分割和变化检测的定性结果对比[18-19], 图中白色区域表示变化区域, 黑色区域表示未变化区域。

|
图 6 数据1多尺度分割及变化检测结果 Figure 6 Multiscale segmentation and change detection results for data 1 |

|
图 7 数据2多尺度分割及变化检测结果 Figure 7 Multiscale segmentation and change detection results for data 2 |

|
图 8 数据3多尺度分割及变化检测结果 Figure 8 Multiscale segmentation and change detection results for data 3 |
从图 6~8可以看出, 叠加图像的SLIC多尺度分割结果比较均匀, 在地物特征分布较为均匀的区域(如水体, 植被等)能得到近乎正方形的地物对象, 而在处理地物分布复杂的区域时不会破坏图像中地物的边界信息, 地物对象不会过于破碎, 较符合真实的地物分布。
通过分析水体周边环境变化检测问题的特点, 有机结合光谱、纹理和指数特征构建混合特征空间, 几种变化检测算法对干扰信息的处理效果都较好。为了更好的对比几种变化检测算法在“伪变化”区域的处理情况, 图 6~8均以椭圆的形式圈出几块包含水质变化或植被物候变化等“伪变化信息”的区域检测结果。通过对比可以看出, 面向对象的变化矢量分析法、基于卡方变换的变化检测方法和基于直方图的变化检测方法的检测结果中容易包含更多的“伪变化信息”, 而本研究算法在“伪变化信息”的处理方面具有较好的效果, 说明几种算法对于水质变化和植被物候变化等“伪变化信息”的检测效果上不如本研究算法。
为更好的验证改进算法在水体周边环境变化检测中的鲁棒性和有效性, 下面对上述变化检测结果进行定量对比分析。
2.2.2 变化检测结果定量对比分析本节以像元数量误差准则来评价变化检测结果的精度, 其中虚检率为误检像元数占检测结果中变化像元总数的比例, 漏检率为漏检像元数占检测结果中未变化的像元总数的比例, 正确率为正确检测的像元数占图像中像元总数的比例, 2.2.1中4种变化检测方案试验结果的精度评定如表 1所示。
| 表 1 不同方法变化检测结果对比 Table 1 Comparison of different methods of change detection |
综合表 1和图 6~8变化检测的检测效果图可以发现, 几种算法处理结果的漏检情况都较少, 将漏检率控制在可接受范围内, 但在误检情况和误检率方面则表现各异:面向对象的变化矢量分析法能够利用多特征空间的各种特征信息, 检测出两时相图像中的大部分变化区域, 但其使用欧氏距离在多特征空间中将各特征信息为等权处理, 未能合理地体现出不同特征表征变化信息的能力, 误检的情况较为严重; 相较变化矢量分析法, 基于卡方变换的变化检测结果的误检情况大大减少; 基于直方图的变化检测结果存在较为严重的误检现象, 原因是两时相图像中的地物特征分布信息受“同物异谱”现象干扰更为严重, 从而影响变化检测结果。在几组数据的变化检测试验中, 基于正反向异质性的算法均取得较好的试验效果和较高的准确率, 同时将误检率控制在较低的范围内, 说明基于正反向异质性的算法对于水体周边环境的变化检测具有较好的检测能力。
3 结论通过对水体边界附近区域进行变化检测, 针对变化检测过程中受到干扰信息和“伪变化信息”影响等问题, 考虑到水体周边环境情况复杂, 水体边界易受人类活动、季节变化等因素的影响产生“伪变化信息”, 进而影响水体周边环境的变化检测, 提出基于正反向异质性的遥感图像变化检测方法。
针对不同时相的遥感图像因成像条件差异、水质变化以及植被物候变化等因素产生“伪变化信息”等问题, 并且考虑到“同物异谱、同谱异物”现象对变化检测结果的干扰, 在光谱与纹理特征的基础上融合水体指数特征和植被指数特征构建针对水体周边环境变化检测的混合特征空间STWV, 在混合特征空间中构建遥感图像地物对象的正反向异质性进行变化检测。首先采用超像素生成算法SLIC处理两时相的叠合影像获取地物对象, 检查地物对象从时相1到时相2的Forward异质性, 再反向检测其从时相2到时相1的Backward异质性, 然后综合正反向的异质信息构建地物对象的正反向异质性, 根据贝叶斯最小错误率理论使用EM算法提取两时相的变化对象, 最后排除植被伪变化信息得到较为准确和鲁棒的变化检测结果。试验结果表明, 该方法能够有效区分水体周边环境中感兴趣的地物变化信息与不感兴趣的干扰信息、“伪变化信息”等, 从而提高水体周边环境的变化检测结果的精度, 找到由于人类活动造成的湖库水域周边“非正常”土地利用变化, 检测精度达96%以上, 为开展基于GF-1水库周边变化检测数据挖掘工作做铺垫。
| [1] | WEN Dawei, HUANG Xin, ZHANG Liangpei, et al. A novel automatic change detection method for urban high-resolution remotely sensed imagery based on multiindex scene representation[J]. IEEE Transactions on Geoscience & Remote Sensing, 2015, 54(1): 609-625 |
| [2] |
佟国峰, 李勇, 丁伟利, 等. 遥感影像变化检测算法综述[J].
中国图象图形学报, 2015, 20(12): 1561-1571 TONG Guofeng, LI Yong, DING Weili, et al. Review of remote sensing image change detection[J]. Journal of Image & Graphics, 2015, 20(12): 1561-1571 DOI:10.11834/jig.20151201 |
| [3] |
辛芳芳, 焦李成, 王桂婷, 等. 基于小波域Fisher分类器的SAR图像变化检测[J].
红外与毫米波学报, 2011, 30(2): 173-178 XIN Fangfang, JIAO Licheng, WANG Guiting, et al. Change detection of SAR images based on wavelet domain Fisher classifier[J]. Journal of Infrared & Millimeter Waves, 2011, 30(2): 173-178 |
| [4] | KOMEIL R, ANUAR A, KARIM S, et al. A new approach for surface water change detection: Integration of pixel level image fusion and image classification techniques[J]. International Journal of Applied Earth Observation & Geoinformation, 2015, 34: 226-234 |
| [5] |
张永梅, 季艳, 马礼, 等. 遥感图像建筑物识别及变化检测方法[J].
电子学报, 2014, 42(4): 653-657 ZHANG Yongmei, JI Yan, MA Li, et al. A recniction and change detection method for building in remote sensing images[J]. Acta Eletronica Sinica, 2014, 42(4): 653-657 |
| [6] | CARLO M, FRANCESCA B, LORENZO B. Building change detection in multi-temporal very high resolution SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2664-2682 DOI:10.1109/TGRS.2014.2363548 |
| [7] |
佃袁勇, 方圣辉, 姚崇怀. 一种面向地理对象的遥感影像变化检测方法[J].
武汉大学学报:信息科学版, 2014, 39(8): 906-912 DIAN Yuanyong, FANG Shenghui, YAO Chonghuai. The geographic object-based method for change detection with remote sensing imagery[J]. Geomatics and Information Science of Wuhan University, 2014, 39(8): 906-912 |
| [8] |
陆苗, 梅洋, 赵勇, 等. 利用多尺度几何特征向量的变化检测方法[J].
武汉大学学报:信息科学版, 2015, 40(5): 623-627 LU Miao, MEI Yang, ZHAO Yong, et al. Change detection based on multi-scale geometric feature vector[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 623-627 |
| [9] | FENG Wengqing, SUI Haigang, TU Jihui. Object-oriented change detection for remote sensing images based on multi-scale fusion[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016, XLI-B7(10): 483-491 |
| [10] | RADHAKRISHNA A, APPU S, AURELIEN L, et al. SLIC superpixels compared to state-of-the-art superpixel methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274-2282 DOI:10.1109/TPAMI.2012.120 |
| [11] |
李亮, 舒宁, 王凯, 等. 融合多特征的遥感影像变化检测方法[J].
测绘学报, 2014, 43(9): 945-953 LI Liang, SHU Ning, WANG Kai, et al. Change detection method for remote sensing images based on multi-features fusion[J]. Acta Geodaetica Et Cartographica Sinica, 2014, 43(9): 945-953 |
| [12] | HU Zhongwen, ZOU Qiu, LI Qingquan. Watershed superpixel[C]//IEEE International Conference on Image Processing (ICIP). New York, USA: IEEE Press, 2015: 349-353. http://dx.doi.org/10.1109/ICIP.2015.7350818 |
| [13] | ZDENEK K, JIRI M, KRYSTIAN M. Tracking-learning-detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1409-1422 DOI:10.1109/TPAMI.2011.239 |
| [14] | ZDENEK K, KRYSTIAN M, JIRI M. Forward-backward error: automatic detection of tracking failures[C]//2010 International Conference on Pattern Recognition (ICPR). New York, USA: IEEE Press, 2010: 2756-2759. http://dl.acm.org/citation.cfm?id=1904935.1905750 |
| [15] | OJALA T, PIETIKAINEN M, MAENPAA T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2000, 24(7): 404-420 |
| [16] | MCFEETERS S K. The use of normalized difference water index(NDWI) in the delineation of open water features[J]. International Journal of Remote Sensing, 1996, 17(7): 1425-1432 DOI:10.1080/01431169608948714 |
| [17] | HUETE A R. A soil-adjusted vegetation index (SAVI)[J]. Remote Sensing of Environment, 1988, 25(3): 295-309 DOI:10.1016/0034-4257(88)90106-X |
| [18] |
贾永红, 谢志伟, 吕臻, 等. 一种新的遥感影像变化检测方法[J].
武汉大学学报:信息科学版, 2016, 41(8): 1001-1006 JIA Yonghong, XIE Zhiwei, LYU Zhen, et al. A new change detection method of remote sensing image[J]. Geomatics and Information Science of Wuhan University, 2016, 41(8): 1001-1006 |
| [19] |
李亮, 龚龑, 李雪, 等. 像斑直方图相似性测度的高分辨率遥感影像变化检测[J].
遥感学报, 2014, 18(1): 139-153 LI Liang, GONG Yan, LI Xue, et al. Change detection based on similarity measurement of object histogram using high-resolution remote sensing imagery[J]. Journal of Remote Sensing, 2014, 18(1): 139-153 |
| [20] | MELNYKOV V, IGOR M. Initializing the EM algorithm in Gaussian mixture models with an unknown number of components[J]. Computational Statistics & Data Analysis, 2012, 56(6): 1381-1395 |
| [21] |
黄春波, 佃袁勇, 周志翔, 等. 基于时间序列统计特性的森林变化监测[J].
遥感学报, 2015, 19(4): 657-668 HUANG Chunbo, DIAN Yuanyong, ZHOU Zhixiang, et al. Forest change detection based on time series images with statistical properties[J]. Joural of Remote Sensing, 2015, 19(4): 657-668 |



