2. 湖北省磁悬浮工程技术研究中心, 湖北 武汉 430070
2. Hubei Provincial Engineering Technology Research Center for Magnetic Suspension, Wuhan 430070, Hubei, China
磁悬浮转子是一种利用磁场力将转子悬浮于空中, 使得定子和转子间没有机械接触, 具有无磨损、不需润滑、无污染、能耗小以及使用寿命长等优点, 特别适用于高速、超高速以及真空等极端环境。但由于开环不稳定, 磁悬浮转子一般采用比例积分微分(proportion integration differentiation, PID)控制算法控制, 可以获得一定的性能。然而, 超高速磁悬浮转子一般要穿越一阶甚至二阶及以上的临界转速并稳定运转, 易造成共振, 且磁轴承定转子间的间隙较小[1], 为避免运转过程中发生动态干涉, 需对磁悬浮转子系统进行精确地控制, 常采用现代控制器(如H∞控制器)。控制器的设计是建立在系统模型的基础上的, 现代控制器的设计需要较精确的动力学模型[2]。然而, 传统的动力学模型较为简单, 忽略了转子间的接触效应, 而转子间配合的过盈量对系统的刚度有较大的影响, 影响系统的固有频率及模态振型等。因此, 为精确建立超高速磁悬浮转子的动力学模型, 进行过盈配合对转子动力学特性的研究尤为重要。
过盈配合属于高度非线性接触[3], ANSYS-workbench模态分析模块会自动忽略非线性接触行为, 故而直接求解会导致结果不准确。目前许多学者针对转子间的接触效应问题做了相关研究, 文献[4-6]针对转子组件是否存在预应力, 采用ANSYS软件对其模态进行了对比研究, 结果表明预应力对转子的固有频率及模态振型等有较大的影响, 且模态阶数越高, 影响越大; 文献[7-12]提出了利用三维接触单元对转子组件进行有限元模态分析, 并通过理论公式、等效静态分析以及模态试验等方式对仿真结果进行了验证, 结果表明考虑转子组件间的接触, 其仿真结果更准确; 文献[13]指出转子的总体刚度受其过盈配合的影响, 忽略接触效应会使得仿真结果不准确; 文献[14]中采用减小附加部件弹性模量的方式来模拟其过盈配合处, 根据经验选择相应的弹性模量, 使得其仿真结果更为准确; 文献[1]针对磁悬浮电机转子系统一体化建模的模态分析误差较大的问题, 提出了考虑转子组件间的非线性接触行为, 基于罚函数方法通过修正优化接触刚度因子实现对电机柔性转子系统模态的精确分析; 文献[15-16]研究了热配合转子的摩擦接触效应对其动力学特性的影响, 表明考虑摩擦接触的仿真分析结果更为准确, 并通过优化过盈配合处的杨氏模量, 设计了一种等效的直接模型, 通过试验证明了该等效模型能较为准确地获取热配合转子的相关动力学参数。但这些研究大多属于后期优化研究, 如何在设计阶段考虑转子间的接触效应, 建立转子精确的动力学模型还有待解决。虽然可以通过试验的方式获得转子相关的动力学特征, 精确其模型, 但试验加工成本较高, 易造成材料的浪费, 增加研制成本。
为此, 本研究采用有限元仿真软件workbench对磁悬浮转子进行带预应力的模态分析, 先采用静力分析模块求解出其由于过盈配合产生的静应力, 再将其作为预应力导入模态分析模块中, 来精确其求解结果。将过盈配合对转子动力学特性的影响看作是通过改变静应力进而影响其动力学特性。对比静应力的仿真值和理论计算值, 优化法向接触刚度因子(FKN), 确定最优的FKN值。通过不断地修正摩擦系数, 使其仿真结果与理论计算结果相当, 确保仿真结果准确可靠。改变磁悬浮转子配合的过盈量, 找出摩擦系数与过盈量的对应关系, 为同类转子的模态精确分析提供参考。
1 磁悬浮转子过盈配合理论分析磁悬浮转子的转速高、离心力大, 为保证能够安全稳定的运行, 其转子和转轴的联接方式为关键因素, 目前常采用过盈配合的联接方式。过盈量的选择对转子的性能有着至关重要的影响:过盈量过大, 装配困难, 会影响接触面的配合效果; 过盈量过小, 可能会使转子松脱, 使得转子运行不稳定。
当转子和转轴间存在过盈量时, 它们接触面就会产生静压力, 设轴的内表面半径为a, 配合面半径为b, 转子外表面半径为c, p为转轴和转子过盈配合面产生的静压力, E为弹性模量, v为泊松比, 转子的径向位移为δ1, 转轴的径向位移为δ2, 配合面的过盈量为Δ, 其装配结构简图如图 1所示。

|
图 1 转子装配结构简图 Figure 1 Structure of the rotor assembly |
| $ \left\{ \begin{array}{l} {\delta _1}{\rm{ = }}\frac{{{b^2}p}}{{E\left( {{c^2}- {b^2}} \right)}}\left[{\frac{{\left( {1 + v} \right){c^2}}}{r} + \left( {1-v} \right)r} \right]\\ {\delta _2} = \frac{{{b^2}p}}{{E\left( {{b^2} - {a^2}} \right)}}\left[{\frac{{\left( {1 + v} \right){a^2}}}{r} + \left( {1-v} \right)r} \right]\\ \Delta = {\delta _1}{|_{r = b}} + {\delta _2}{|_{r = b}} = \frac{{bp}}{E}\left( {\frac{{{c^2} + {b^2}}}{{{c^2} -{b^2}}} + \frac{{{b^2} + {a^2}}}{{{b^2} -{a^2}}}} \right) \end{array} \right.。$ | (1) |
磁悬浮转子以角速度ω旋转时, 由于转子的半径大于转轴的半径, 其离心力大于转轴的离心力, 故而转子内径的扩大变形比转轴外径扩大变形大, 且转速越高, 变形差值越大[20-21]。当离心力产生的变形差值等于转子和转轴间过盈量时, 转子和转轴将发生松脱现象。旋转时转子的径向位移为δ′1, 转轴的径向位移为δ′2, 配合面的过盈量减少量为Δ′, 则
| $ \begin{array}{l} {{\delta '}_1} = \frac{{\left( {3- 2v} \right)\left( {1 + v} \right)}}{{8E\left( {1- v} \right)}}\rho {\omega ^2}r \cdot \\ \;\;\;\;\;\;\;\left[{\left( {1-2v} \right)\left( {{c^2} + {b^2}} \right) + \frac{{{c^2}{b^2}}}{{{r^2}}}-\frac{{1-2v}}{{3 - 2v}}{r^2}} \right], \end{array} $ |
| $ \begin{array}{l} {{\delta '}_2} = \frac{{\left( {3- 2v} \right)\left( {1 + v} \right)}}{{8E\left( {1- v} \right)}}\rho {\omega ^2}r \cdot \\ \;\;\;\;\;\;\;\left[{\left( {1-2v} \right)\left( {{a^2} + {b^2}} \right) + \frac{{{a^2}{b^2}}}{{{r^2}}}-\frac{{1-2v}}{{3 - 2v}}{r^2}} \right], \end{array} $ |
| $ \Delta ' = {\delta '_1}{|_{r = b}}-{\delta '_2}{|_{r = b}} = \frac{{\left( {3-2v} \right)\left( {1 + v} \right)}}{{4E}}\rho {\omega ^2}b\left( {{c^2}-{a^2}} \right), $ |
则转子组件的动态过盈量
| $ {\Delta _1} = \Delta-\Delta ', $ |
式中ρ为材料的密度。本研究中转子和转轴的材料都选用45#钢, 其弹性模量为2.09 GPa, 泊松比为0.269, 密度为7 890 kg/m3。以转速60 000 r/min的磁悬浮转子为例进行研究, 带入方程可求出在该转速下, 为保证转子不松脱, 其最小静态过盈量Δ=0.025 98 mm。此外, 为保证磁悬浮转子能够稳定的运行, 其过盈配合的最大压力应不超过材料的屈服强度。由式(1)可得出:
| $ p = \frac{{E\Delta \left( {{c^2}-{b^2}} \right)\left( {{b^2}-{a^2}} \right)}}{{2{b^3}\left( {{c^2}-{a^2}} \right)}}。$ | (2) |
本研究中转轴为实心轴时, 即a=0, 应力与过盈量的关系为
| $ p = \frac{{E\Delta \left( {{c^2}-{b^2}} \right)}}{{2b{c^2}}}, $ |
则需要满足p≤σs, 求得Δ=0.104 04mm。故本研究以0.026 mm~0.104 mm范围内的过盈量进行研究分析。
2 磁悬浮转子有限元模型的建立磁悬浮转子基本构件如图 2、3所示, 转子和转轴的材料都为45#钢。

|
图 2 转轴结构图 Figure 2 Structure of the shaft |

|
图 3 转子结构图 Figure 3 Structure of the rotor |
转轴和转子的尺寸参数如表 1所示, 其中i表示过盈量, 过盈量不同时, 转子孔的直径也不同。
| 表 1 转轴和转子的尺寸参数 Table 1 Size of the shaft and rotor |
与一般的分析不同, 考虑接触效应的仿真分析过程中需创建接触对, 在选择接触表面时需遵循相应的原则:当凸面与平面或凹面接触时, 应选择平面或凹面为目标面[22-23]。故而本研究中选择转轴的外表面为接触面, 转子的内表面为目标面。网格划分一律采用映射面划分的方式, 单元尺寸设置为5 mm, 避免因网格划分不一致而导致对结果影响。磁悬浮转子的三维模型及其网格划分结果如图 4所示。

|
图 4 转子组件有限元网格划分模型 Figure 4 The mesh of the finite element modal ofrotor-shaft assembly |
在静力分析模块中, 将转轴两端固定约束, 防止其移动, 求出该转子因过盈配合产生的静应力; 在模态分析模块中, 取消静力分析中的固定约束, 采用自由约束, 从而得到转子的固有频率及振型等。
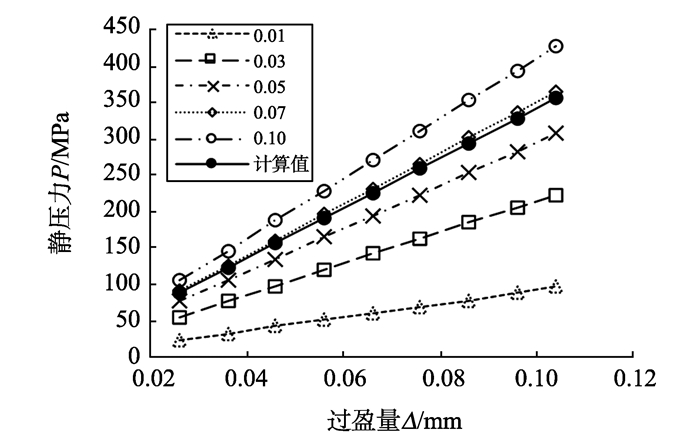
3 磁悬浮转子静力仿真结果分析 3.1 接触刚度因子的优化在接触仿真分析问题中, 接触刚度因子(FKN)是一个较为重要的参数, 通常系统中默认为自动设置, 在考虑接触问题时可根据实际进行修改。一般对于绑定和不分离的线性接触问题, 默认FKN=10;以体积为主的非线性接触问题, 默认FKN=1;以弯曲为主的非线性接触问题, 设置FKN=0.01~0.1[22-23]。本研究旨在分析磁悬浮转子的动力学特性, 故而取FKN=0.01~0.1。选择几组不同的FKN值, 得出其静应力随过盈量的对应关系, 并与不同过盈量下静应力的理论计算结果进行对比, 其结果如图 5所示。
|
图 5 静应力理论值和不同FKN下仿真值随过盈量的变化曲线 Figure 5 The curve of the theoretical value and different FKNsimulation value of static stress and the interference |
从图 5可以看出, 在相同过盈量下, 随着FKN值的增加, 其静应力也增加。当FKN=0.07时, 其静应力仿真值与理论计算值较为接近。进一步细化FKN的取值, 当FKN=0.066 5时, 其仿真结果与理论计算结果基本一致, 其结果如表 2所示。故而在随后的仿真分析中, 将接触刚度因子设置为0.066 5, 精确其仿真结果。
| 表 2 静应力的仿真值与理论值 Table 2 Simulation and theoretical values of the static stress |
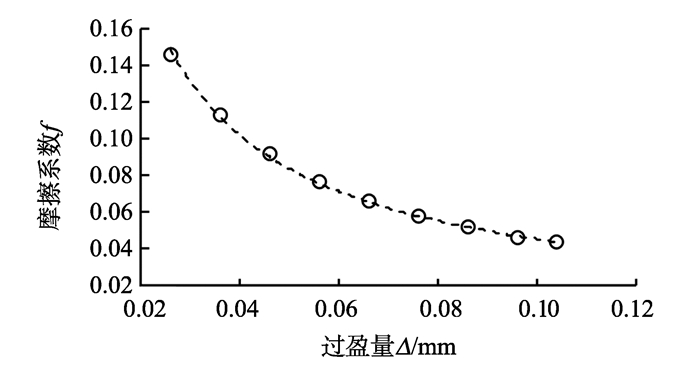
虽然通过优化FKN的方式可以精确其模型, 得到较为准确的仿真值。但对于现代控制器, 系统模型越精确, 其控制效果越好, 为满足某些高精度控制场合, 需得到更加精确的模型。而对于过盈配合的转子, 由于接触面压力的存在, 材料会发生变形, 在不同过盈量下接触面的压力也有所不同, 从而引起转子不同的表面形状变化。当形变结束后, 转子接触表面压力会根据过盈量重新分布, 从而引起摩擦系数的变化。为此, 在设定最优FKN的情况下, 通过修正摩擦系数的方式, 进一步优化转子模型。在有限元模型中, 给定某一过盈量, 不断改变摩擦系数, 将其仿真结果与理论计算值进行对比, 找出其结果相当时对应的摩擦系数。改变过盈量, 重复上述步骤, 得出过盈量与摩擦系数的一一对应点, 并拟合其关系曲线如图 6所示。
|
图 6 过盈量与摩擦系数的关系曲线 Figure 6 The curve of the interference and the friction coefficient |
由图 6可知, 过盈量与摩擦系数的对应点基本都在拟合曲线上, 表明该曲线能够较好地拟合过盈量与摩擦系数之间的关系。通过该曲线得出过盈量和摩擦系数的关系式为:
| $ f = 0.0059{\Delta ^{-0.887}}。$ | (3) |
当给定转子配合的过盈量时, 即可通过式(3)求出其对应的摩擦系数, 使得仿真结果准确可靠。因此可以在设计过程中对磁悬浮转子进行较为准确地仿真分析, 从而优化其结构。
4 磁悬浮转子模态仿真结果分析以磁悬浮转子配合过盈量为0.026 mm为例, 针对其是否考虑接触效应, 对磁悬浮转子进行模态仿真分析。
4.1 不考虑接触效应的模态仿真在不考虑接触的情况下, 即磁悬浮转子为一体化模型, 改变其过盈量, 对模型没有影响。可直接使用workbench中的模态分析模块进行仿真分析, 选出其前三阶固有频率分别为983.07、2 249.2和4 714.7 Hz, 最大相对位移分别为44.66、42.675和44.255 mm。其对应的模态振型分别如图 7~9所示。

|
图 7 磁悬浮转子第一阶模态振型 Figure 7 The first mode shape of the rotor-shaft assembly |

|
图 8 磁悬浮转子第二阶模态振型 Figure 8 The second mode shape of the rotor-shaft assembly |

|
图 9 磁悬浮转子第三阶模态振型 Figure 9 The third mode shape of the rotor-shaft assembly |
从振型图中可以看出, 第一阶模态振型有两个节点, 其形状像碗形; 第二阶模态振型有三个节点, 其形状像“S”形; 第三阶模态振型有四个节点, 其形状像“W”形。
4.2 考虑接触效应的模态仿真在考虑接触效应的情况下, 按照前述方式进行带预应力的模态仿真分析。根据式(3)可求出在过盈量Δ=0.026 mm时, 其对应的摩擦系数值为0.146 5。仿真过程中设置相应的过盈量及对应的摩擦系数, 对其进行求解。选出其前三阶固有频率分别为860.56 Hz、2 147.6 Hz和4 346.7 Hz, 最大相对位移分别为43.181 mm、41.203 mm和44.046 mm。
4.3 模态仿真结果对比和分析将不考虑接触效应和考虑接触效应这两种情形下磁悬浮转子的模态分析结果进行对比, 其前三阶固有频率和最大位移如表 3、4所示。
| 表 3 磁悬浮转子固有频率结果对比 Table 3 The contrast of the magnetic levitation rotors’ natural frequency |
| 表 4 磁悬浮转子最大相对位移结果对比 Table 4 The contrast of the magnetic levitation rotors’ maximum relative displacement |
由表 3可以看出, 是否考虑接触效应对模态仿真结果影响较大, 其中前三阶固有频率最大误差高达14.24%;在不考虑接触效应的情况下, 其固有频率明显比考虑接触效应时的大。究其原因是由于在不考虑接触效应的情况下, 其模型等效为一体化模型, 总刚度比实际过盈配合转子的刚度大。在无阻尼自由振动情形下, 转子固有频率满足:丨K-ω2M丨=0。故当总刚度偏大时, 由于其总质量不变, 计算出的固有频率值也相应的偏大; 此外, 不考虑接触效应时, 模态振型的最大相对位移误差虽然较小, 但考虑到对于磁悬浮转子, 其工作气隙一般都较小, 而由于模型不精确造成的振型相对误差易使得其控制难以满足使用要求, 容易造成动态干涉, 从而损坏设备。对比表 3、表 4数据可知, 考虑磁悬浮转子间的接触效应, 能够有效地精确转子模型, 使得求解更加准确。
5 结论为避免超高速磁悬浮转子在运行过程中共振或与磁轴承发生动态干涉的情况, 需对其进行精确地控制。为此, 磁悬浮转子精确动力学模型的建立尤为重要。而传统的一体化建模方法模型简单, 误差较大。故而本研究考虑了过盈配合磁悬浮转子间的接触效应, 进而优化其动力学模型。
(1) 通过改变FKN值, 得出了在不同FKN值下, 磁悬浮转子因过盈配合产生的静应力和过盈量之间的关系曲线。结合理论计算和静力仿真分析结果, 确定了磁悬浮转子模态分析的最优FKN值。
(2) 在设定最优FKN值下, 通过不断地修正摩擦系数, 进一步优化磁悬浮转子模型。找出了转子过盈量与摩擦系数的关系曲线, 为同类转子的模态精确分析提供参考, 从而可以在设计阶段优化转子模型。
(3) 针对是否考虑磁悬浮转子间的接触效应, 分别对转子进行了模态仿真分析。结果表明:考虑和不考虑接触效应, 对磁悬浮转子固有频率影响较大, 对最大相对位移的影响相对较小, 且不考虑接触效应时, 转子的固有频率明显偏大; 考虑转子间的接触效应能够有效的精确其动力学模型, 使求解准确可靠。
| [1] |
黄梓嫄, 韩邦成, 周银锋. 非线性接触下磁悬浮电机柔性转子系统模态分析[J].
中国电机工程学报, 2014, 34(15): 2438-2444 HUANG Ziyuan, HAN Bangcheng, ZHOU Yinfeng. Modal analysis of the flexible rotor system of magnetic levitation motors under nonlinear contact[J]. Proceedings of the Csee, 2014, 34(15): 2438-2444 |
| [2] |
龙亚文, 谢振宇, 徐欣. 磁悬浮轴承H∞鲁棒控制策略研究[J].
振动与冲击, 2013, 32(23): 115-120 LONG Yawen, XIE Zhenyu, XU Xin. H∞ robust control strategy for an active magnetic bearing[J]. Journal of Vibration & Shock, 2013, 32(23): 115-120 DOI:10.3969/j.issn.1000-3835.2013.23.021 |
| [3] |
张秀华. 高速储能飞轮转子的过盈配合分析[J].
煤矿机械, 2012, 33(10): 150-152 ZHANG Xiuhua. Analysis of interference fit of high-speed energy storing flywheel rotor[J]. Coal Mine Machinery, 2012, 33(10): 150-152 |
| [4] |
王林军, 曹慧萍. 基于ANSYS-Workbench的转子模态分析[J].
三峡大学学报(自然科学版), 2014, 36(6): 89-93 WANG Linjun, CAO Huiping. Modal analysis of rotor based on ANSYS-Workbench[J]. Journal of China Three Gorges University (Natural Sciences), 2014, 36(6): 89-93 |
| [5] |
刘君, 袁建平. 带预应力的高速离心泵转子模态分析[J].
中国农村水利电, 2014, 32(2): 117-121 LIU Jun, YUAN Jianping. A modal analysis of the rotor of high-speed centrifugal pumps with prestress[J]. China Rural Water & Hydropower, 2014, 32(2): 117-121 |
| [6] |
刘正锐, 黄勤, 宋祎平. 微型电机转子的过盈配合分析[J].
煤矿机械, 2011, 32(5): 100-101 LIU Zhengrui, HUANG Qin, SONG Yiping. Interference fits analysis of micro motor rotor[J]. Coal Mine Machinery, 2011, 32(5): 100-101 |
| [7] |
万俟昊天, 向阳, 夏雪宝, 等. 过盈配合面的接触刚度和接触阻尼计算研究[J].
船海工程, 2013, 42(3): 85-90 MOQI Haotian, XIANG Yang, XIA Xuebao, et al. Research on calculation of contact stiffness and contact damping of interference-fit interface[J]. Ship & Ocean Engineering, 2013, 42(3): 85-90 |
| [8] |
张建水, 殷玉枫, 赵肖敏, 等. 基于ANSYS的轴套过盈配合接触分析[J].
机械设计, 2014, 31(5): 21-25 ZHANG Jianshui, YIN Yufeng, ZHAO Xiaomin, et al. Contact analysis of interference fit between shaft and shaft sleeve based on ANSYS[J]. Journal of Machine Design, 2014, 31(5): 21-25 |
| [9] |
寇海江, 袁惠群, 李岩, 等. 一体化转子系统动力分析的预应力模态综合法[J].
东北大学学报(自然科学版), 2014, 35(2): 263-267 KOU Haijiang, YUAN Huiqun, LI Yan, et al. A prestressed component mode synthesis method for dynamics analysis of blisk-shaft integrated rotor[J]. Journal of Northeastern University(Natural Science), 2014, 35(2): 263-267 |
| [10] |
安吉阁, 李建宾, 廖熠. 基于ANSYS转子曲轴过盈配合有限元分析[J].
机械工程师, 2010, 32(11): 119-120 AN Jige, LI Jianbin, LIAO Yi. Finite element analysis of interference joint of rotor and crankshaft based on ANSYS[J]. Mechanical Engineer, 2010, 32(11): 119-120 DOI:10.3969/j.issn.1002-2333.2010.11.053 |
| [11] |
李小彭, 赵光辉, 杨皓天, 等. 考虑结合面影响的组合梁非线性预应力模态分析[J].
振动与冲击, 2014, 33(4): 17-21 LI Xiaopeng, ZHAO Guanghui, YANG Haotian, et al. Nonlinear prestressed modal analysis for a composite beam considering influence of joint surface[J]. Journal of Vibration & Shock, 2014, 33(4): 17-21 |
| [12] | CHEN S Y. The dynamic analyses and verifications of a hollowshaft with hot-fit component using 3d finite contact element[J]. Transactions-Canadian Society for Mechanical Engineering, 2013, 37(1): 21-38 DOI:10.1139/tcsme-2013-0002 |
| [13] | CHEN S Y, KUNG C, LIAO T T, et al. Dynamic effects of the interference fit of motor rotor on the stiffness of a high speed rotating shaft[J]. Transactions-Canadian Society for Mechanical Engineering, 2014, 34(34): 243-261 |
| [14] |
李红伟, 于文涛, 刘淑琴. 基于ANSYS的磁悬浮挠性转子模态分析与设计[J].
中国机械程, 2014, 25(11): 1447-1452 LI Hongwei, YU Wentao, LIU Shuqin. Mode analysis and design of maglev flexible rotor with ANSYS[J]. China Mechanical Engineering, 2014, 25(11): 1447-1452 |
| [15] | CHEN S Y, KUNG C, HSU J C. Dynamic analysis of a rotary hollow shaft with hot-fit part using contact elements with friction[J]. Transactions-Canadian Society for Mechanical Engineering, 2011, 35(3): 461-474 DOI:10.1139/tcsme-2011-0026 |
| [16] | CHEN S Y. An equivalent direct modeling of a rotary shaft with hot-fit components using contact element modal analysis results[J]. Computers & Mathematics with Applications, 2012, 64(5): 1093-1099 |
| [17] |
丁鸿昌, 肖林京, 张华宇, 等. 高速永磁电机转子护套过盈配合量计算及应力分析[J].
机械设计与研究, 2011, 27(5): 95-98 DING Hongchang, XIAO Linjing, ZHANG Huayu, et al. Interference fit calculation and stress analysis for rotor sleeve of high-speed permanent magnet electric machine[J]. Machine Design & Research, 2011, 27(5): 95-98 |
| [18] |
同剑, 原大宁, 刘宏昭, 等. 电主轴与其内装转子过盈配合的可靠性分析[J].
机械科学与技术, 2013, 32(6): 845-852 TONG Jian, YUAN Daning, LIU Hongzhao, et al. The reliability analysis of motorized spindle and motor rotor with interference fit[J]. Mechanical Science & Technology for Aerospace Engineering, 2013, 32(6): 845-852 |
| [19] |
史忠震, 张卫, 陈强, 等. 高速微型永磁电机转子护套过盈配合的计算与分析[J].
微特电机, 2014, 42(4): 35-37 SHI Zhongzhen, ZHANG Wei, CHEN Qiang, et al. Interference fit calculation and analysis for rotor sleeve of high-speed micro permanent magnet electric motor[J]. Small & Special Electrical Machines, 2014, 42(4): 35-37 |
| [20] |
王伟, 尤磊. 电机转子过盈配合分析计算[J].
湖南农机:学术版, 2013, 40(1): 37-38 WANG Wei, YOU Lei. Analysis on interference fit of rotation of electrical motor rotor[J]. Hunan Agricultural Machinery, 2013, 40(1): 37-38 |
| [21] |
郭铁能, 马小超, 谷昀超, 等. 轴承过盈配合量对主轴动力学特性的影响[J].
北京工业大学学报, 2016, 42(1): 51-59 GUO Tieneng, MA Xiaochao, GU Yunchao, et al. Effect of the interference fit amount impact on the dynamic characteristics of spindle[J]. Journal of Beijing University of Technology, 2016, 42(1): 51-59 DOI:10.11936/bjutxb2015060037 |
| [22] | 凌桂龙. ANSYS Workbench 15.0从入门到精通[M]. 北京: 清华大学出版社, 2014: 325-350. |
| [23] | 高长银, 李万全, 刘丽. ANSYS Workbench 14.5建模与仿真从入门到精通[M]. 北京: 电子工业出版社, 2014: 351-359. |




