2. 南京磁谷科技有限公司, 江苏 南京 211102
2. Nanjing CIGU Co., Ltd, Nanjing 211102, Jiangsu, China
磁悬浮推力轴承系统作为磁悬浮离心式压缩机的作动器, 可通过调整压缩机叶轮与蜗壳之间的间隙来实现喘振控制。但是磁悬浮推力轴承系统在压缩机运转过程中会受到大的气压扰动[1], 因此将磁悬浮推力轴承用于喘振控制需要能控制转子精确跟踪轴向位置并且具有较强的抗干扰能力。H∞控制是在磁悬浮轴承系统中用得最多的现代控制算法之一, 合理设计H∞控制器能够为系统提供较强的鲁棒性, 在干扰和不确定性影响下使系统能保持较好的性能[2]。H∞鲁棒控制器的设计依赖于精确的被控对象模型, 以及对系统各模块不确定性的度量, 所以在设计过程中如何得到精确的模型以及各模块不确定性范围是关键问题[3-4]。
V-Gap度量方法一般用来描述两个模型间的相近程度, 也是对不确定集合的面向控制的量化描述[5]。V-Gap度量引入的闭环系统性能测量指标——广义稳定裕度, 能够比较控制器与被控对象的闭环稳定性能, 分析两个被控对象的闭环性能“相近程度”[6-7]。文献[8]提出将V-Gap度量不确定性和广义稳定裕度引入反馈系统实现控制器设计; 文献[9]将V-Gap度量引入不确定性反馈, 对H∞鲁棒性和H∞回路成形控制器设计进行了详尽描述; 文献[10]利用V-Gap度量对磁悬浮轴承-转子系统中存在的不确定性分析评估, 建立了相应的不确定性模型; 文献[5]在引入广义稳定裕度稳定性要求基础上提出了V-Gap度量评估飞行控制律的步骤, 但缺少相应的试验验证; 文献[11]提出利用V-Gap方法定义辨识模型误差, 给出迭代控制器设计的鲁棒稳定条件和控制器迭代辨识优化方法, 但迭代辨识的不确定模型集合和计算量较大。由上述可知, 对于V-Gap度量引入反馈系统鲁棒性分析研究有一定的理论基础, 但对于不确定性系统的反馈控制设计研究较少, 并且缺乏相应的试验研究。
本研究针对该问题, 对磁悬浮推力轴承系统建模分析, 基于V-Gap度量设计H∞控制器, 以达到改善磁悬浮推力轴承的干扰抑制和位置跟踪能力的目的。整个控制器设计过程分为被控对象建模、不确定模型分析、广义稳定裕度评估和控制器设计。在V-Gap度量分析不确定性基础上将广义稳定裕度评估与控制器设计过程结合, 可充分考虑系统参数的摄动情况。仿真和试验结果显示设计后的H∞控制器抗干扰能力和位置跟踪性能得到改善。
1 V-Gap度量和广义稳定裕度V-Gap度量, 又称Vinnicombe Gap, 用符号δv表示, 能直观地量化两系统间差异程度。V-Gap度量可以简单理解为两个系统在频域上的差异[12-13]。
两个对象G1、G2之间的V-Gap度量定义为:
| $ {\delta _{\rm{V}}}\left( {{G_1},{G_2}} \right) = \left\{ \begin{array}{l} {\left\| {\kappa \left( {{G_1}\left( {{{\rm{e}}^{{\rm{j}}\omega }}} \right),{G_2}\left( {{{\rm{e}}^{{\rm{j}}\omega }}} \right)} \right)} \right\|_\infty }\\ \;\;\;\;\;\;\;\;\;如果式(2), (3)成立。\\ 1,否则 \end{array} \right. $ | (1) |
| $ \det \left( {1 + G_1^ \sim {G_2}} \right)\left( {{{\rm{e}}^{{\rm{j}}\omega }}} \right) \ne 0, $ | (2) |
| $ {\rm{wno}}\left( {1 + G_1^ \sim {G_2}} \right) + \eta \left( {{G_2}} \right) - \tilde \eta \left( {{G_1}} \right) = 0. $ | (3) |
式中:G~(ejω)=G(e-jω); η(G)表示G的开右半平面极点数;
| $ \begin{array}{l} \kappa \left( {{G_1}\left( {{{\rm{e}}^{{\rm{i}}\omega }}} \right),{G_2}\left( {{{\rm{e}}^{{\rm{i}}\omega }}} \right)} \right) = \\ \;\;\;\;\;\;\;\frac{{\left| {{G_1}\left( {{{\rm{e}}^{{\rm{i}}\omega }}} \right),{G_2}\left( {{{\rm{e}}^{{\rm{i}}\omega }}} \right)} \right|}}{{\sqrt {1 + {{\left| {{G_1}\left( {{{\rm{e}}^{{\rm{i}}\omega w}}} \right)} \right|}^2}} \sqrt {1 + {{\left| {{G_2}\left( {{{\rm{e}}^{{\rm{i}}\omega }}} \right)} \right|}^2}} }}。\end{array} $ | (4) |
δv(G1, G2)是对已知控制器情况下G1、G2的闭环稳定性能相近程度的测量。因此, 本研究对于给定一个镇定G1的名义控制器C, 引入广义稳定裕度。
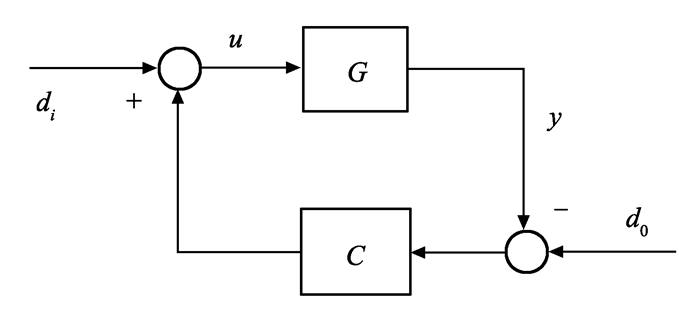
对于给定闭环控制系统[G, C], 如图 1所示, 定义其广义稳定裕度[5]:
| $ b\left( {G,C} \right) = \left\{ \begin{array}{l} \left\| {M\left( {G,C} \right)} \right\|_\infty ^{ - 1},如果\left( {G,C} \right)稳定\\ 0,否则 \end{array} \right., $ | (5) |
|
图 1 典型的闭环控制系统结构图 Figure 1 Classical structure diagram of close loop control system |
式中, M(G, C)定义为
| $ M\left( {G,C} \right) = \left[ {\begin{array}{*{20}{c}} G\\ I \end{array}} \right]{\left( {1 - GC} \right)^{ - 1}}\left[ {\begin{array}{*{20}{c}} { - C}&I \end{array}} \right]。$ | (6) |
式(5)对应的频域广义稳定裕度定义为
| $ \begin{array}{l} b\left( {G\left( {{\rm{j}}\omega } \right),C\left( {{\rm{j}}\omega } \right)} \right) = \\ \left\| {\left[ {\begin{array}{*{20}{c}} {G\left( {{\rm{j}}\omega } \right)}\\ I \end{array}} \right]{{\left( {I - C\left( {{\rm{j}}\omega } \right)G\left( {{\rm{j}}\omega } \right)} \right)}^{ - 1}}\left[ {\begin{array}{*{20}{c}} { - C\left( {{\rm{j}}\omega } \right)}&I \end{array}} \right]} \right\|_\infty ^{ - 1}。\end{array} $ | (7) |
对于系统[G, C], 定义系统最优广义稳定裕度
| $ {b_{\rm{s}}}\left( {G\left( {{\rm{j}}\omega } \right),C\left( {{\rm{j}}\omega } \right)} \right) = \mathop {\inf }\limits_{w \in R} b\left( {G\left( {{\rm{j}}\omega } \right),C\left( {{\rm{j}}\omega } \right)} \right)。$ | (8) |
对于控制系统而言, 控制器设计要求应该满足稳定裕度要求, 一般取bs(G, C)≥0.3。
对于给定对象G0, G1∈Rp×q, 和能够镇定对象的控制器C, V-Gap值与广义稳定裕度有如下关系[16]:
| $ b\left( {{G_1},C} \right) \ge b\left( {{G_0},C} \right) - {\delta _{\rm{V}}}\left( {{G_0},{C_1}} \right)。$ | (9) |
式(9)表明V-Gap度量能反映系统的鲁棒性, 可得到以下结论:若两对象间的V-Gap度量值很小, 则能稳定其中一个对象的控制器也较易稳定另一对象; 反之, 很难找到能同时稳定两个对象的控制器。
V-Gap度量具有以下特点[5]:
(1) 有清晰的频域概念, 能够在频域中分析系统的性能;
(2) 可以直观分析参数摄动对系统鲁棒性的影响;
(3) 可用于计算各参数摄动对系统的影响程度, 忽略次要元素, 减少计算量。
2 磁悬浮推力轴承系统建模和不确定性分析由于H∞控制器设计是基于模型的, 被控对象模型的准确性直接影响控制器性能。为了合理地设计控制器, 需要对被控对象模型进行研究, 即对电磁铁-转子、传感器、功率放大器以及控制器模型进行分析[17]。本研究试验对象为磁悬浮轴承-转子试验平台, 如图 2所示。

|
图 2 磁悬浮轴承-转子试验平台 Figure 2 Magnetic bearing-rotor test rig 1—计算机; 2—信号发生器; 3—磁悬浮控制箱; 4—数据采集卡; 5—电流转接箱; 6—磁悬浮轴承-转子试验台; 7—传感器电路; 8—数字控制器; 9—模拟控制器; 10—功放电路 |
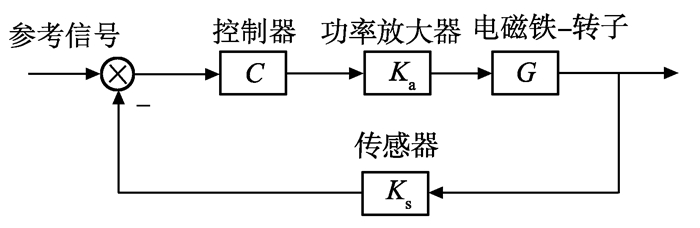
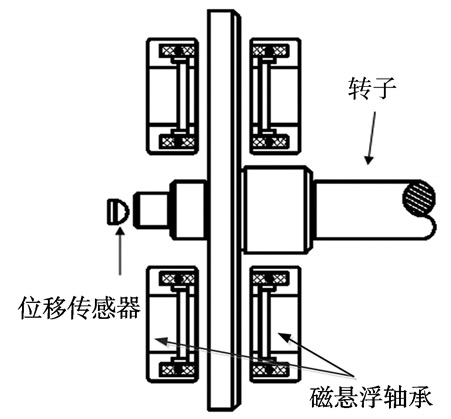
磁悬浮轴承-转子系统如图 3所示, 推力轴承结构如图 4所示, 利用位移传感器检测出转子偏离参考点的位移, 控制器根据偏差计算出控制信号, 然后功率放大器将控制信号转换为控制电流, 驱动电磁铁产生力, 使转子悬浮在给定位置上[18-19]。图 3中C为控制器, Ka为功率放大器, G为电磁铁-转子, Ks为传感器。
|
图 3 磁悬浮轴承-转子系统图 Figure 3 Magnetic bearing-rotor system |
|
图 4 磁悬浮推力轴承结构 Figure 4 Structure of magnetic thrust bearing |
在稳定工作点附近, 通过对轴承力—位移—电流进行小范围的线性化, 得到电磁铁-转子的传递函数[20]
| $ G = \frac{{{k_{\rm{i}}}}}{{m{s^2} - {k_{\rm{x}}}}}, $ | (10) |
式中:m表示转子质量, m=14.56 kg; kx和ki分别表示磁悬浮轴承的位移刚度和电流刚度, 表达式为:
| $ {k_{\rm{i}}} = \frac{{{\mu _0}A{N^2}{I_0}}}{{C_0^2}}, $ | (11) |
| $ {k_{\rm{x}}} = \frac{{{\mu _0}A{N^2}I_0^2}}{{\delta _0^3}}, $ | (12) |
式中:μ0为真空磁导率; A表示径向磁悬浮轴承单级磁极面积;N表示径向磁悬浮轴承单级线圈匝数; I0表示径向磁悬浮轴承偏置电流; δ0表示径向磁悬浮轴承与转子的平衡间隙。具体参数如表 1所示。
| 表 1 磁悬浮推力轴承部分参数 Table 1 Some parameters of magnetic thrust bearing |
本研究采用的电涡流位移传感器带宽为5 kHz, 而转子轴向位置跟踪频率较低, 位移传感器可以视为理想的比例环节。轴向传感器的位移行程为0~0.9 mm, 输出为0 ~5 V, 传感器的增益
| $ {K_{\rm{s}}} = 50000/9\left( {{\rm{V}}/{\rm{m}}} \right)。$ | (13) |
功率放大器采用电压-电流型三电平PWM开关功放。本研究通过信号发生器扫频试验测试分析得到功率放大器的幅频特性。根据试验测得的功率放大器频响特性, 用3阶数学模型进行辨识, 得到传递函数[21]
| $ {K_{\rm{a}}} = \frac{{0.0420{s^3} + 3979{s^2} + 8.737 \times {{10}^6}s + 1.505 \times {{10}^9}}}{{{s^3} + 9251{s^2} + 6.451 \times {{10}^6}s + 1.098 \times {{10}^9}}}。$ | (14) |
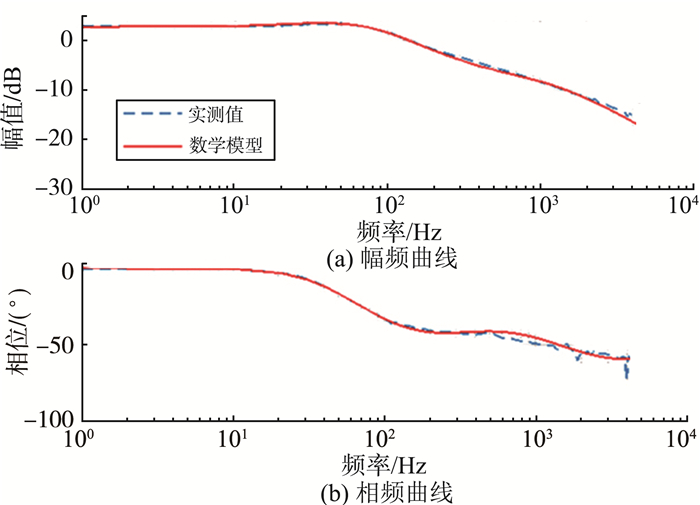
图 5为功率放大器实测频域响应与理论模型对比由图 5可知,误差较小, 该模型能准确反映功放特性。
|
图 5 功率放大器实测频域响应与理论模型对比 Figure 5 Comparison between the measured frequency response and theoretical model of power amplifier |
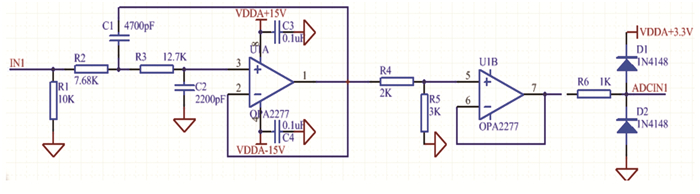
本研究采用的基于DSP的数字控制系统的硬件部分在位移输入信号前处理电路中增加了抗混叠滤波电路, 在控制信号后处理电路中增加了平滑滤波等, 以及DSP芯片本身和A/D、D/A转换等环节。首先对信号前处理电路进行建模, 见图 6。
|
图 6 数字控制器位移信号前处理电路 Figure 6 Preprocessing circuit of digital controller displacement signal |
分析图 6可知, 位移信号电压范围为0~5 V, DSP芯片输入电压范围为0~3.3 V, 为避免信号由于限幅而失真, 在进行信号抗混叠滤波处理后, 对信号进行分压处理, 即根据比例缩小信号幅值。理论推导平滑滤波环节和分压环节传递函数得到:
| $ {G_{{\rm{pp}}}}\left( s \right) = \frac{{0.6}}{{9.132 \times {{10}^{ - 10}}{s^2} + 4.22 \times {{10}^{ - 5}}s + 1}}。$ | (15) |
在控制器中时滞产生的原因主要有两方面, 其一是A/D和D/A转换所耗费的时间, 其二是控制器计算所耗费的时间。将DSP芯片以及D/A转换模块的数学模型简化为时滞传递函数[22], 为时滞传递函数串联一个比例项, 得到DSP芯片以及D/A转换模块的数学模型
| $ {G_{\rm{D}}}\left( s \right) = {k_{\rm{d}}}{{\rm{e}}^{ - s{k_t}{T_{\rm{s}}}}}, $ | (16) |
式中:kt为滞后时间系数, kd为增益项。通过修正kt与kd系数来得到更精确的数学模型。e-sktTs无法用标准的传递函数形式表示, 这里采用二阶Pade近似[23], 取kt=1.1, kd=3.35, 采样时间为Ts=0.000 1 s, 得到近似的数学模型:
| $ {G_{\rm{D}}}\left( s \right) \approx {k_{\rm{d}}}\frac{{{{\left( {0.3175{T_{\rm{s}}}s - 1} \right)}^2}}}{{{{\left( {0.3175{T_{\rm{s}}}s + 1} \right)}^2}}} = \frac{{3.35{{\left( {0.3175 \times {{10}^{ - 4}}s - 1} \right)}^2}}}{{{{\left( {0.3175 \times {{10}^{ - 4}}s - 1} \right)}^2}}}。$ | (17) |
磁悬浮轴承是开环不稳定的, 因此稳定性问题尤为重要。考虑不确定性的鲁棒稳定性是磁悬浮轴承-转子系统控制器设计的重要要求[6]。
控制器的设计决定了磁悬浮轴承支承的等效刚度和等效阻尼, 以及转子能否正常悬浮, 磁悬浮轴承能否稳定工作。为了更好地抑制线性化导致的参数不确定性, 以及功率放大器、位移传感器受电路本身和外界温度的影响而存在的参数不确定性, 本研究采用V-Gap度量分析各个参数不确定性影响, 在控制器设计过程中考虑参数不确定性, 保证控制器的鲁棒性能。
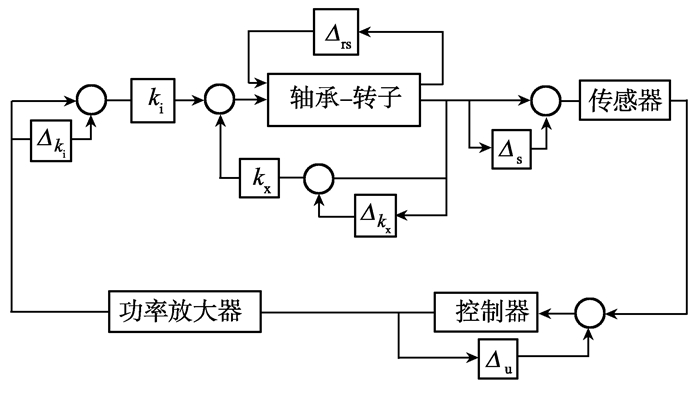
2.2.1 不确定性描述系统的不确定性是指系统的数学模型和实际间的差别。本研究根据实际系统来定各个环节不确定性, 由于实际系统的不确定性是非结构不确定性, 所以就把它们近似为参数不确定性, 有以下几个部分, 如图 7, 转子结构模态的不确定性、磁悬浮轴承电磁力线性化产生的不确定性、位移传感器和功率放大器电路本身和因外界温度的影响存在参数不确定性以及数字控制器A/D和D/A部分时延不确定性。
|
图 7 磁悬浮推力轴承系统参数不确定性表征 Figure 7 Parameter uncertainty characterizations of magneticthrust bearing system |
根据文献[10], 在转子结构模态中, 建模误差Δrs取1%~3%, 本研究取不确定量为3%。电磁力线性化会带来一定的误差, 这种误差会导致电流-力系数ki和位移-力系数kx的参数摄动, 摄动量Δki和Δkx取5%~10%。本研究取不确定量为10%。
功率放大器电路和传感器电路受电路本身和外界温度影响, 存在一定的参数摄动。功率放大器和传感器电路参数摄动可综合考虑成传感器的参数摄动。传感器探头采集误差为±2%, 探头的线性误差为±1%。文献[10]中将传感器的不确定量定在1%~3%。本研究取位移传感器和功率放大器的不确定量Δs为5%。A/D和D/A部分时延不确定性, 在上节中通过Pade近似简化为时滞的传递函数, 取时延不确定量Δu为10%。
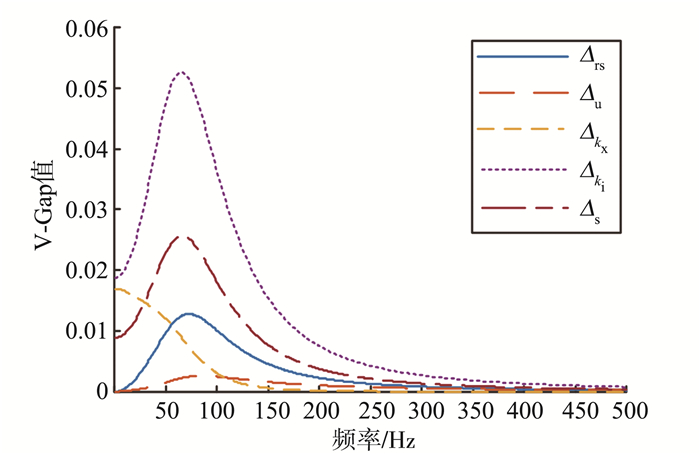
2.2.2 不确定性分析对上节中所选取的参数不确定性采用V-Gap度量对比摄动系统与标称系统的开环动态特性。根据式(4)求得各个参数分别摄动的最坏情况下, 其频域V-Gap度量值曲线, 见图 8。得到的各个参数摄动的V-Gap结果见表 2。
|
图 8 各参数摄动下频域V-Gap度量结果 Figure 8 V-Gap metric results under the parameter perturbations in frequency domain |
| 表 2 各个参数摄动的V-Gap值 Table 2 V-Gap metric results under the parameter perturbations |
从图 8可以看出, 所取的时延不确定性相对于其他参数不确定性, 对被控对象开环系统影响较小, 因此可忽略其摄动影响。在控制器设计过程中, 可将其余参数不确定性考虑进被控对象模型中保证控制器的鲁棒稳定性和鲁棒性能。
3 磁悬浮推力轴承系统H∞控制器设计本研究根据式(9)以广义稳定裕度为稳定性要求, 提出通过V-Gap度量方法保证设计后系统的鲁棒性能。推力轴承系统H∞控制器设计过程如下:
(1) 对试验系统被控对象各环节建模分析;
(2) 通过V-Gap度量方法分析各参数摄动对系统的影响程度, 忽略次要元素, 在控制器设计过程中考虑主要摄动参数的不确定性;
(3) 选择合适的加权函数, 通过Matlab求解H∞控制器, 比较仿真分析出的H∞控制器与被控对象模型的广义稳定裕度是否满足bs(G′s, C)≥0.3, 若满足, 直接转(4), 若不满足则重新设计控制器;
(4) 试验分析对比控制器鲁棒性能和位置跟踪性能。
稳定性要求bs(G′s, C)≥0.3, 根据式(9)得到, 满足
| $ {b_{\rm{s}}}\left( {{{G'}_{\rm{s}}},C} \right) \ge {b_{\rm{s}}}\left( {{G_{\rm{s}}},C} \right) - {\delta _{\rm{v}}}\left( {{{G'}_{\rm{s}}},{C_{\rm{s}}}} \right) \ge 0.3。$ |
G′s为考虑参数不确定性后的被控对象模型, Gs为名义模型。
根据第二节确定含有不确定性的电流-力系数, 位移-力系数, 模型参数, 传感器参数分别为:
| $ {{k'}_{\rm{i}}} = {k_{\rm{i}}}\left( {1 + {\Delta _{{k_{\rm{i}}}}}{p_{{k_{\rm{i}}}}}} \right),{{k'}_{\rm{x}}} = {k_{\rm{x}}}\left( {1 + {\Delta _{{k_{\rm{x}}}}}{p_{{k_{\rm{x}}}}}} \right), $ |
| $ m' = m\left( {1 + {\Delta _{{\rm{rs}}}}{p_{{\rm{rs}}}}} \right),{{K'}_{\rm{s}}} = {K_{\rm{s}}}\left( {1 + {\Delta _{\rm{s}}}{p_{\rm{s}}}} \right), $ |
式中, pki, pkx, prs, ps分别代表各个参数的相对扰动, 满足-1≤pki, pkx, prs, ps≤1。
将参数的不确定性考虑到被控对象模型中得到:
| $ {{G'}_{\rm{s}}}\left( s \right) = {{K'}_{\rm{s}}}\left( s \right) \cdot {K_{\rm{a}}}\left( s \right) \cdot {G_{{\rm{pp}}}}\left( s \right) \cdot {G_{\rm{D}}}\left( s \right) \cdot G'\left( s \right), $ | (18) |
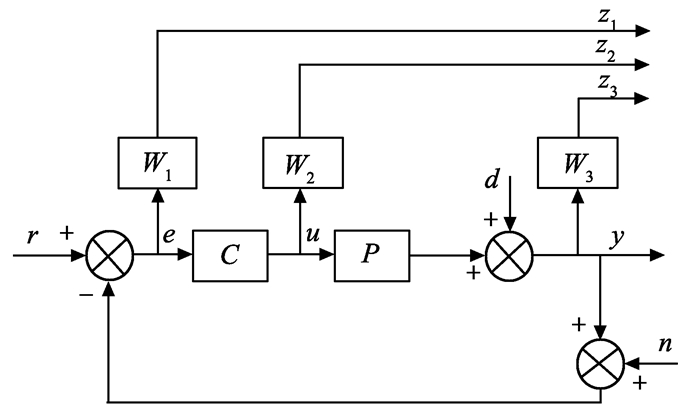
根据文献[24-25], 设计混合灵敏度H∞控制器, 通过合理的选择加权函数来设计控制器, 使控制器与被控对象组成的闭环系统满足要求, 如图 9所示。
|
图 9 混合灵敏度H∞控制示意图 Figure 9 Schematic diagram of mixed sensitivity H∞ control |
选取一定的加权函数后, 计算H∞控制器, 其中P为考虑参数不确定性的广义被控对象, 包括了实际被控对象和权函数。最终计算得到的控制器传递函数
| $ C = \frac{{ - 2.663 \times {{10}^5}{s^3} - 4.865 \times {{10}^8}{s^2} - 7.911 \times {{10}^{11}}s - 3.106 \times {{10}^{12}}}}{{4444{s^3} + 1.386 \times {{10}^7}{s^2} + 2.142 \times {{10}^{10}}s - 9.79 \times {{10}^8}}}。$ | (19) |
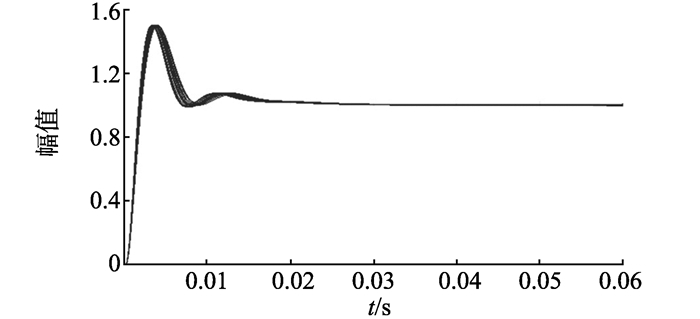
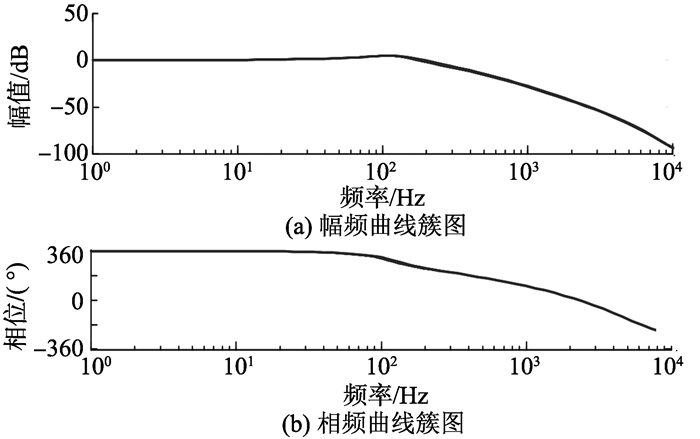
图 10和图 11为存在参数摄动下, 磁悬浮推力轴承H∞控制的阶跃响应和闭环系统频率响应簇图。可以发现, 考虑参数不确定性后得到的H∞控制器, 具有一定的鲁棒性能和抗干扰能力。
|
图 10 阶跃响应簇图 Figure 10 Step response cluster diagram |
|
图 11 磁悬浮推力轴承系统频率响应簇图 Figure 11 Frequency response cluster diagram of magneticthrust bearing system |
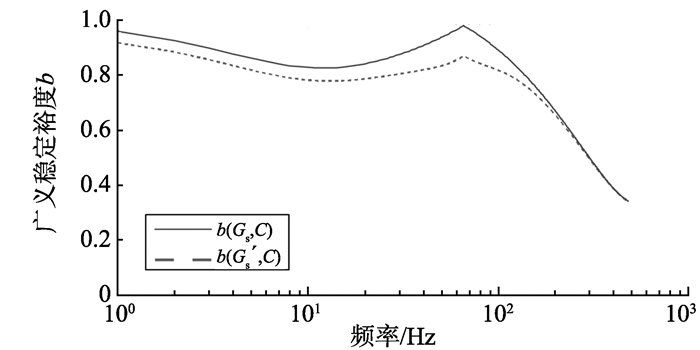
图 12为该控制器与被控对象的频域广义稳定裕度。磁悬浮推力轴承系统的工作频率范围在0~300 Hz左右, 从图中可知满足稳定性要求bs(G′s, C)≥0.3。
|
图 12 系统频域广义稳定裕度图 Figure 12 Generalized stability margin diagram of systemin frequency domain |
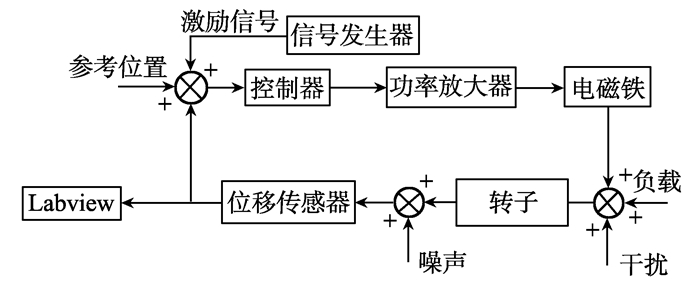
如图 13, 通过进一步的试验分析对比设计后H∞控制器的鲁棒稳定性和位置跟踪能力。
|
图 13 位置跟踪试验原理图 Figure 13 Principle diagram of position tracking experiment |
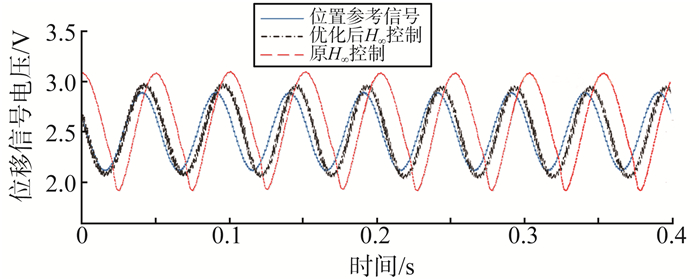
如图 14为设计前后H∞控制器的位置跟踪试验对比。在20 Hz, 0.4 V的激振信号下, 分析位置跟踪结果来对比系统的位置跟踪性能, 得到在控制器设计前后, 转子振幅分别为0.60 V和0.45 V, 振幅减少了25%。可以看出, 在重新设计H∞控制器后, 位置跟踪误差更小, 系统鲁棒稳定性能更好。
|
图 14 H∞控制器20 Hz正弦信号位置跟踪对比 Figure 14 Comparison of H∞ controller position tracking performance under 20 Hz sinusoidal signals |
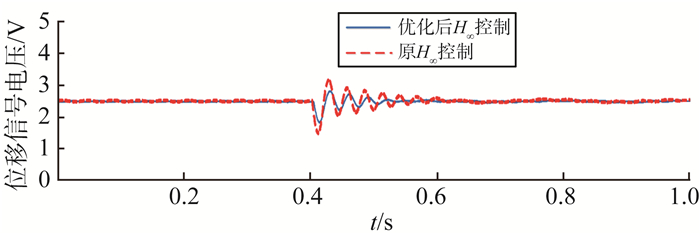
如图 15为转子悬浮在2.5 V中间位置进行冲击试验对比。由图 15可知, 在相同冲击载荷下, 转子都能恢复到稳定位置。在H∞控制器设计前后, 转子受到冲击后轴向最大位移分别为1.00 V和0.65 V, 调节时间分别为0.20 s和0.12 s, 最大偏移减少了35%, 调节时间减少了40%, 说明重新设计后H∞控制器抗干扰能力得到提高。
|
图 15 H∞控制器悬浮在2.5 V位置冲击试验对比 Figure 15 Comparison of the impact test of H∞ controller at the 2.5 V position |
本研究给出了基于V-Gap度量分析实际系统建模过程中参数不确定性, 并在此基础上以广义稳定裕度为稳定性要求来实现控制器设计的方法, 并进行了试验验证。在V-Gap度量基础上将广义稳定裕度稳定性要求用于控制器设计, 可在充分考虑参数摄动情况下, 分析各参数摄动对系统的影响程度, 忽略影响小的参数摄动来减少计算量。仿真和试验结果表明, 基于V-Gap度量设计的H∞鲁棒控制器, 在同样激振信号下振幅减少约25%, 相位差减小, 在同样干扰下调节时间减少约40%, 控制器抗干扰能力和位置跟踪性能都得到改善。
本研究中时延不确定性主要根据控制器理论模型与实际模型的差异来确定, 不够准确, 需要进一步研究。同时, 本研究给出的V-Gap度量H∞鲁棒控制器设计过程中, 仍需要试验对控制器加权函数进行选择, 过程繁琐, 后续可以进一步研究以广义稳定裕度为稳定性要求对加权函数寻优的H∞鲁棒控制器设计方法。
| [1] |
唐茂, 周瑾, 崔恒斌. 磁悬浮离心式压缩机的推力轴承喘振控制[J].
自动化仪表, 2017, 38(5): 15-19 TANG Mao, ZHOU Jin, CUI Hengbin. Surge control of the centrifugal compressor with magnetic thrust bearing[J]. Process Automation Instrumentation, 2017, 38(5): 15-19 |
| [2] |
王恩平, 黄琳, 耿志勇. 一类参数不确定性系统的鲁棒控制[J].
自动化学报, 2001, 27(1): 70-74 WANG Enping, HUANG Lin, GENG Zhiyong. Robust stabilization for a class of system with parametric uncertainties[J]. Acta Automatica Sinica, 2001, 27(1): 70-74 |
| [3] |
李蒙, 石泳, 刘莉. 基于鲁棒H∞的无人机飞行控制系统设计及实现[J].
北京理工大学学报, 2016, 36(8): 807-812 LI Meng, SHI Yong, LIU Li. Development of UAV auto pilot based on robust H∞ theory[J]. Transaction of Beijing Institute of Technology, 2016, 36(8): 807-812 |
| [4] |
周丽娜, 刘晓华. 不确定中立型随机时滞系统的鲁棒记忆非脆弱H∞控制[J].
山东大学学报(工学版), 2013, 43(3): 49-56 ZHOU Lina, LIU Xiaohua. Robust memory state feedback non-fragile H∞ control of an uncertain neutral stochastic time-delay systems[J]. Journal of Shandong University (Engineering Science), 2013, 43(3): 49-56 |
| [5] |
刘林, 纪多红, 唐强. V-Gap度量及其在飞行控制律评估中的应用[J].
航空学报, 2007, 28(4): 930-93 LIU Lin, JI Duohong, TANG Qiang. V-Gap metric and its application to clearance of flight control laws[J]. Acta Aeronautica ET Astronautica Sinica, 2007, 28(4): 930-93 |
| [6] | VINNICOMBE G. The robustness of feedback systems with bounded complexity controllers[J]. IEEE Transactions on Automatic Control, 2002, 41(6): 795-803 |
| [7] | DOYLE J. Analysis of feedback systems with structured uncertainties[J]. IEE Proceedings D-Control Theory and Applications, 1982, 129(6): 242-250 DOI:10.1049/ip-d.1982.0053 |
| [8] | VINNICOMBE G. A V-Gap distance for uncertain and nonlinear systems[C]//Proceedings of the 38th Conference on Decision and Control. Phoenix, USA: IEEE, 1999. |
| [9] | VINNICOMBE G. Uncertainty and feedback H∞ loop shaping and the V-Gap metric[C]//International Conference on Fuzzy Systems & Knowledge Discovery. Melbourne, Australia: IEEE, 2001: 1438-1441. |
| [10] | LI G. Robust stabilization of rotor-active magnetic bearing systems[D]. Virginia, USA: University of Virginia, 2007. |
| [11] |
宗群, 窦立谦, 刘文静. 基于Vinnicombe距离的迭代辨识与控制设计[J].
自动化学报, 2008, 34(11): 1431-1436 ZONG Qun, DOU Liqian, LIU Wenjing. Iterative identification and control design based on Vinnicombe distance[J]. Acta Automatica Sinica, 2008, 34(11): 1431-1436 |
| [12] |
刘斌, 王常虹, 李伟. 间隙度量与跟踪系统中的鲁棒控制器设计[J].
控制与决策, 2010, 25(11): 1713-1718 LIU Bin, WANG Changhong, LI Wei. Gap metric and robust controller design in tracking systems[J]. Control and Decision, 2010, 25(11): 1713-1718 |
| [13] | GENG Lihui, CUI Shigang, ZHAO Li. Frequency-domain worst-case identification of multiple input multiple output errors-in-variables models[J]. Control Theory and Applications, 2016, 33(10): 1366-1372 |
| [14] |
顾晓宇. 基于V-Gap度量的迭代辨识与控制方法研究[D]. 天津: 天津大学, 2007.
GU Xiaoyu. Research on iterative identification and control method based on V-Gap metric[D]. Tianjin: Tianjin University, 2007. http: //cdmd. cnki. com. cn/Article/CDMD-10056-2008185670. htm |
| [15] | GlOVER K, VINNICOMBE G, PAPAGEORIOU G. Guaranteed multi-loop stability margins and the gap metric[C]//Decision and Control, 2000. Proceedings of the IEEE Conference on. Sydney, Australia: IEEE, 2000, 4: 4084-4085. |
| [16] | STEELE J, VINNICOMBE G. Advanced techniques for clearance of flight control laws[M]. Berlin & Heidelberg, Germany: Springer-Verlag, 2002. |
| [17] |
孙云. 磁悬浮轴承控制系统研究[D]. 南京: 南京理工大学, 2014.
SUN Yun. Research on magnetic bearing control system[D]. Nanjing: Nanjing University of Science and Technology, 2014. http: //cdmd. cnki. com. cn/article/cdmd-10288-1014175173. htm |
| [18] |
谢振宇, 徐龙祥, 李迎, 等. 磁悬浮轴承转子系统动态特性的试验研究[J].
航空动力学报, 2004, 19(1): 30-37 XIE Zhenyu, XU Longxiang, LI Ying, et al. Analysis of radial dynamic characteristics of magnetic bearing system by excitation test[J]. Journal of Aerospace Power, 2004, 19(1): 30-37 |
| [19] | CHU K C, WANG Y, WILSON J, et al. Modeling and control of a magnetic bearing system[C]//American Control Conference. Baltimore, USA: IEEE, 2010: 2206-2211. |
| [20] |
李书鹏. 磁悬浮轴承系统的鲁棒H∞控制研究[D]. 南京: 南京航空航天大学, 2007.
LI Shupeng. Robust H∞ control of magnetic bearing system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007. http: //cdmd. cnki. com. cn/Article/CDMD-10287-2007194308. htm |
| [21] |
王军, 徐龙祥. 磁悬浮轴承开关功率放大器等效数学模型[J].
电工技术学报, 2010, 25(4): 53-58 WANG Jun, XU Longxiang. Equivalent mathematical models of switch power amplifier for magnetic bearing[J]. Transactions of China Electrotechnical Society, 2010, 25(4): 53-58 |
| [22] | MUSHI S E. Robust control of rotor dynamic instability in rotating machinery supported by active magnetic bearings[D]. Virginia, USA: University of Virginia, 2012. |
| [23] |
吕志民, 周茂林. 使用Pade近似式处理数字控制系统中的纯滞后[J].
中山大学学报(自然科学版), 2001, 40(1): 114-115 LYU Zhiming, ZHOU Maolin. Manipulation of the pure time delay in digital control system applying Pade approximation[J]. Acta Scientiarum Naturalium Universititatis Sunyatseni, 2001, 40(1): 114-115 |
| [24] |
杨志勇, 王广雄. MIMO系统混合灵敏度设计的问题[J].
控制理论与应用, 1999, 16(2): 238-240 YANG Zhiyong, WANG Guangxiong. Problem with mixed sensitivity design of MIMO system[J]. Control Theory and Applications, 1999, 16(2): 238-240 |
| [25] | CERONE V, MILANESE M, REGRUTO D. Yaw stability control design through a mixed-sensitivity approach[J]. IEEE Transactions on Control Systems Technology, 2009, 17(5): 1096-1104 DOI:10.1109/TCST.2008.2005402 |




