磁轴承是利用可控电磁力将转子稳定悬浮在空间的一种新型高性能轴承, 具有无接触、无润滑、无磨损、高转速、功耗低、维护简单等优点, 广泛应用于机械工业领域, 如涡轮分子泵、高速离心机、涡轮发电机、磁悬浮硬盘、磁悬浮飞轮储能、高速数控机床等各种高速旋转机械[1-5]。径向磁轴承的磁极数直接关系到承载力的大小和空间利用率, 必须进行优化设计。径向磁轴承通常可采用8、12、16、24、32磁极的结构, 不同的磁极数对磁轴承的性能产生不同的影响, 例如影响轴承的气隙磁通密度、承载力、损耗、磁极之间的磁耦合、空间大小等, 而这些因素的变化都可以归结为磁极数对磁力轴承磁场分布以及磁力的影响[6]。目前, 有不少学者针对磁极布置形式对磁轴承的损耗、磁场和磁力的影响展开了理论分析和试验研究[7-12]。本研究针对不同直径的转子, 分别设计不同磁极数的径向磁轴承结构。利用电磁场有限元分析软件仿真其磁场分布和电磁力, 分析了磁极数对径向磁轴承承载力的影响。
1 径向磁轴承设计依据及设计结果典型的径向磁轴承结构如图 1所示。
|
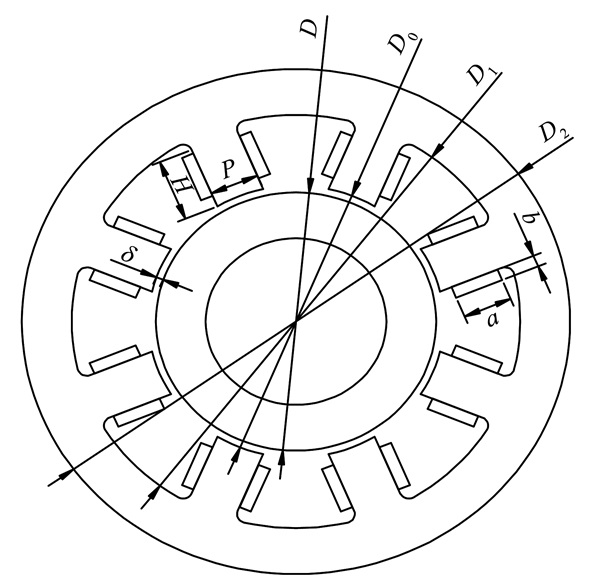
图 1 径向磁轴承结构图
Figure 1 The structure of radial magnetic bearing
D—转子直径; D0—定子内径; D1—定子中径;
D2—定子外径; H—定子窗口深度; P—极靴宽度; a—线圈长度; b—线圈宽度 |
铁磁材料一般有硅钢片、钢、永磁铁等, 为了获得良好的特性, 电磁轴承的定子及转子采用的铁磁材料应该具有饱和磁密大、相对磁导率大、体电阻大、铁损低且便于加工等特点[13]。硅钢片能较好地满足这几方面的要求, 广泛用于磁轴承的铁芯材料。
1.2 磁极数径向磁轴承磁极数直接影响承载力和体积, 并影响系统损耗。磁极数的设计原则是使磁轴承具有良好的电气性能、较低的功耗、简单的制造工艺等[6]。在实际设计过程中, 定子铁芯的磁极数可参考表 1[14]。
| 表 1 转子直径与磁极数选用参考 Table 1 The reference of rotor diameter andthe number of poles |
径向磁轴承按磁极的排列方向分为轴向布置和周向布置。周向布置的电磁铁轴向尺寸小, 结构紧凑, 周向空间利用充分, 是目前广泛采用的结构形式[7]。周向布置又分为NSSN周向布置和NSNS周向布置两种形式, 在转子旋转过程中NSSN周向布置的磁力线方向在一个周期内改变次数少, 其损耗小, 是目前广泛采用的形式。
1.4 气隙电磁力与气隙的平方成反比, 在满足承载力为首要目的情况下, 应该尽量减小定子与转子之间的气隙, 通常气隙值可依据表 2[9, 15]选取。
| 表 2 气隙选取与转子直径的关系 Table 2 The relationship between air gap and rotor diameter |
当取定子极靴宽度和槽口宽度相等时, 极靴宽度
| $ P = \frac{{\pi {D_0}}}{{2{N_{\rm{p}}}}}, $ |
式中Np为磁极数。
1.6 磁轴承宽度径向磁轴承最大承载力
| $ {F_{\rm{m}}} = {k_{\rm{r}}}\frac{{B_{\rm{m}}^2A}}{{2{\mu _0}}}, $ |
式中: kr为合力系数; Bm为最大气隙磁感应强度; A为单个磁极面积; μ0为真空中的磁导率。当Np=8时, kr=1.847 8;当Np=16时, kr=3.640 0;当Np=24时, kr=5.417 4;当Np=32时, kr=7.214 1。
单个磁极面积
| $ A = \frac{{2{F_{\rm{m}}}{\mu _0}}}{{{k_r}B_{\rm{m}}^2}}, $ |
则磁轴承宽度
| $ L = \frac{A}{P}。$ |
导线的直径取决于流过它的电流有效值, 导线的最小直径
| $ d = \sqrt {\frac{{4{I_{{\rm{max}}}}}}{{\pi J}}} , $ |
式中:J为漆包线的电流密度, 一般取J=4~6 A/mm2, 本研究中J=6 A/mm2; Imax为导线最大许用电流, 本研究中Imax=4 A。
一对电磁铁线圈的匝数
| $ N = \frac{{2{B_{\rm{m}}}\delta }}{{{\mu _0}{I_{{\rm{max}}}}}}, $ |
式中δ为气隙。
实际线圈腔面积
| $ {A_{{\rm{cu}}}} = \frac{{\pi {d^2}N}}{{4\eta }}, $ |
式中η为槽满率。根据实际工程经验, 当极靴端设置绕组卡槽时, 一般η=0.4;当极靴端不设置绕组卡槽时, 一般η=0.5。本研究中η=0.4。
根据实际工程经验, 绕组端距离定子中径端和极靴端均留有3~5 mm的间隔, 本研究中取4 mm。
则线圈长度
| $ a = \frac{{H - 8}}{d}, $ |
线圈宽度
| $ b = \frac{{{N_1}}}{a}, $ |
式中N1为单极电磁铁线圈匝数。
1.8 定子窗口深度径向电磁轴承定子窗口深度
| $ H = \frac{{\sqrt {D_0^2 + 8{N_{\rm{p}}}\frac{{{A_{{\rm{cu}}}}}}{\pi }} - {D_0}}}{2}。$ |
按照径向磁轴承参数设计依据, 设计了不同转子直径、不同磁极数的径向磁轴承, 其理论承载力均为500 N, 最大气隙磁感应强度均为1.2 T, 静态工作电流均为2 A, 导线直径均为1 mm, 设计结果见表 3。
| 表 3 径向磁轴承设计结果 Table 3 The designed results of radial magnetic bearing |
为了分析研究不同直径的转子、磁极数对径向磁轴承承载力的影响, 本研究利用电磁场有限元分析软件分别建立转子直径为40、70、150、200 mm, 磁极数为8、12、16的二维仿真模型, 仿真磁场分布和电磁力。
2.1 径向磁轴承静磁场有限元模型根据表 3建立几何模型。为了考虑磁轴承外围的漏磁, 在轴承的定子外建立5 mm厚的空气层模型[16-17]。磁轴承的物理模型包括定子、转子、转轴、线圈、空气层五部分[18-19], 分别设置相应的材料属性为:定子和转子由型号为35W250的硅钢片叠成, 转轴的材料为45#钢, 线圈材料为铜, 空气层材料为空气。加载电流激励并在磁轴承空气层的外边缘加载磁力线平行的边界条件, 最后设置相关的求解参数并进行仿真计算[20]。
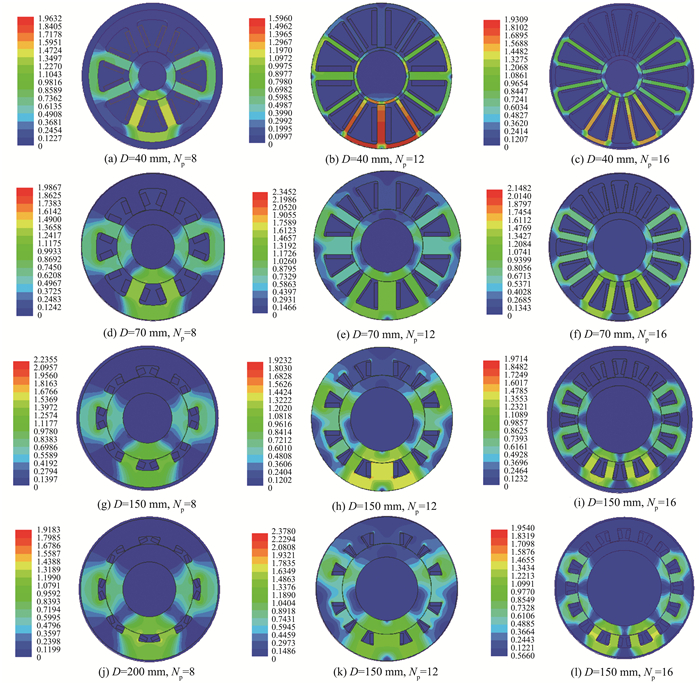
2.2 径向磁轴承静磁场有限元计算图 2为径向磁轴承磁感应强度分布图(图中单位为T), 仿真计算结果见表 4。
|
图 2 径向磁轴承磁感应强度分布图 Figure 2 The magnetic induction distribution of radial magnetic bearing |
| 表 4 径向磁轴承磁场计算结果 Table 4 The magnetic field calculation results ofradial magnetic bearing |
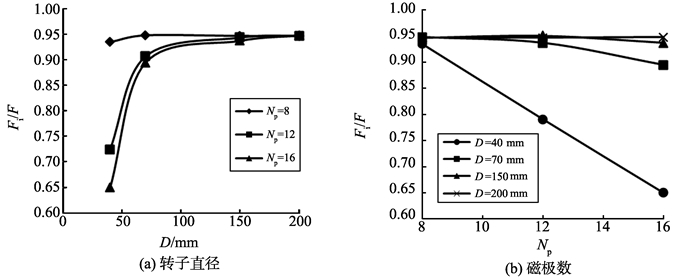
根据表 4, 绘制了转子直径及磁极数对径向磁轴承承载力的影响趋势图, 如图 3所示。
|
图 3 转子直径及磁极数对磁轴承承载力的影响 Figure 3 The effect of rotor diameter and number of poles on capacity of magnetic bearing |
图 3表明:当转子直径为40 mm时, 随着磁极数的增加, 磁轴承的承载力呈线性迅速减小; 当转子直径为70、150 mm时, 随着磁极数的增加, 径向磁轴承的承载力也有明显减小, 但幅度较小; 当转子直径达到200 mm时, 随着磁极数的增加径向磁轴承的承载力几乎不变。
3 结论本研究以实际工程经验为基础, 设计了不同转子直径和不同磁极数的径向磁轴承结构。使用电磁场有限元分析方法针对不同转子直径不同磁极数的径向磁轴承模型进行了仿真计算, 对比分析了不同转子直径下磁极数对径向磁轴承承载力的影响。得出以下结果:
(1) 在径向磁轴承结构设计过程中, 当转子直径达到70 mm后, 12磁极的径向磁轴承具有轴向尺寸小的优点。
(2) 当转子直径不超过150 mm时, 磁极数对径向磁轴承的承载力影响较大, 承载力随着磁极数的增加显著减小。所以在径向磁轴承设计过程中, 以满足承载力为首要目的时, 可优先选用8磁极结构。
(3) 当转子直径达到150 mm时, 磁极数对径向磁轴承的承载力并无明显的影响。
| [1] |
张维煜, 朱熀秋, 袁野. 磁悬浮轴承应用发展及关键技术综述[J].
电工技术学报, 2015, 30(12): 12-20 ZHANG Weiyu, ZHU Huangqiu, YUAN Ye. Study on key technologies and applications of magnetic bearings[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 12-20 DOI:10.3969/j.issn.1000-6753.2015.12.002 |
| [2] |
李媛媛, 朱熀秋, 朱利东. 磁悬浮轴承发展及关键技术研究现状[J].
微电机, 2014(6): 69-73 LI Yuanyuan, ZHU Huangqiu, ZHU Lidong. Development and research status of key technologies on magnetic bearings[J]. Micromotors, 2014(6): 69-73 |
| [3] | 施韦策G, 布鲁勒H, 特拉克斯勒A. 主动磁轴承基础、性能及应用[M]. 虞烈, 袁祟军, 译. 北京: 新时代出版社, 1997: 1-22. |
| [4] | GERHARD Schweitzer, ERICH Maslen. 磁悬浮轴承: 理论、设计及旋转机械应用[M]. 徐旸, 张剀, 赵雷, 译. 北京: 机械工业出版社, 2012: 1-25. |
| [5] | 胡业发, 周祖德, 江征风. 磁力轴承的基础理论与应用[M]. 北京: 机械工业出版社, 2006: 1-5. |
| [6] |
丁国平, 胡业发, 周祖德. 径向磁力轴承磁极布置对磁场和磁力的影响[J].
中国机械工程, 2008, 19(19): 2364-2367 DING Guoping, HU Yefa, ZHOU Zude. Effects of magnetic pole arrangement on magnetic field and force in radial magnetic bearings[J]. China Mechanical Engineering, 2008, 19(19): 2364-2367 DOI:10.3321/j.issn:1004-132X.2008.19.022 |
| [7] |
吴刚, 张育林, 刘昆. 电磁轴承结构参数设计研究[J].
机械科学与技术, 2005, 24(6): 713-715 WU Gang, ZHANG Yulin, LIU Kun. Research on structure parameter design of electromagnetic bearings[J]. Mechanical Science and Technology, 2005, 24(6): 713-715 |
| [8] |
蔡敏, 朱熀秋. 轴向磁轴承参数设计与性能分析[J].
微电机, 2010, 43(10): 22-25 CAI Min, ZHU Huangqiu. Parameter design and performance analysis for axial magnetic bearing[J]. Micromotors, 2010, 43(10): 22-25 DOI:10.3969/j.issn.1001-6848.2010.10.007 |
| [9] | MIZUNO T, HIGHCHI T. Experimental measurement of rotational losses in magnetic bearings[C]// Proceedings of 4th International Symposium on Magnetic Bearings. Zurich, Switzerland: 4th International Symposium on Magnetic Bearings, 1994: 591-595. |
| [10] | STEPHENS L S, KNOSPE C R. Effects of magnetic pole arrangement on core loss in laminated high-speed magnetic journal bearings[J]. IEEE Transactions on Magnetics, 1996, 32(4): 3246-3252 DOI:10.1109/20.508388 |
| [11] |
张云鹏, 刘淑琴, 李红伟. 基于磁路分析的轴向混合磁轴承径向承载力解析计算[J].
电工技术学报, 2012, 27(5): 137-142 ZHANG Yunpeng, LIU Shuqin, LI Hongwei. Calculation of radial electromagnetic force of axial hybrid magnetic bearing based on magnetic circuit analysis[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 137-142 |
| [12] |
占智军. 主动电磁轴承的设计与分析[D]. 杭州: 浙江大学, 2013: 8.
ZHAN Zhijun. Design and analysis of active magnetic bearings[D]. Hangzhou: Zhejiang University, 2013: 8. |
| [13] |
陈浩. 电磁轴承系统的设计与研究[D]. 北京: 北京工业大学, 2009: 18.
CHEN Hao. Design and research on the magnetic bearing system[D]. Beijing: Beijing University of Technology, 2009: 18. |
| [14] |
朱坤. 磁悬浮转子虚拟样机中结构设计系统的研究与开发[D]. 武汉: 武汉理工大学, 2007: 22-26.
ZHU Kun. Research and development of structural design on magnetic suspension rotor's virtual prototype[D]. Wuhan: Wuhan University of Technology, 2007: 22-26. http://cdmd.cnki.com.cn/Article/CDMD-10497-2007147756.htm |
| [15] |
汤银龙. 600 Wh飞轮储能系统的电磁轴承结构设计[D]. 哈尔滨: 哈尔滨工程大学, 2013: 25.
TANG Yinlong. Structure design of the active magnetic bearing based on 600 Wh flywheel energy storage system[D]. Harbin: Harbin Engineering University, 2013: 25. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014132368.htm |
| [16] | 赵博, 张洪亮. Ansoft 12在工程电磁场中的应用[M]. 北京: 中国水利水电出版社, 2013: 2-44. |
| [17] |
丁国平, 周祖德, 胡业发. 磁力轴承旋转电磁场的有限元计算及分析[J].
武汉理工大学学报, 2012, 34(1): 114-117 DING Guoping, ZHOU Zude, HU Yefa. Calcuulation and analysis of magnetic bearings rotating magnetic field with field element method[J]. Journal of Wuhan University of Technology, 2012, 34(1): 114-117 |
| [18] |
李泽辉, 滕万庆, 李翀. 磁悬浮储能飞轮用径向磁轴承磁路仿真分析[J].
储能科学与技术, 2014, 3(4): 308-311 LI Zehui, TENG Wanqing, LI Chong. Finite element analysis of a magnetic circuit of radial magnetic bearing for magnetically suspended flywheels[J]. Energy Storage Science and Technology, 2014, 3(4): 308-311 |
| [19] |
杨芳芳, 吕建超. 推力磁轴承的优化设计与有限元分析[J].
燃气涡轮试验与研究, 2010, 23(2): 43-46 YANG Fangfang, LYU Jianchao. Optimization design and finite element analysis for thrust magnetic bearings[J]. Gas Turbine Experiment and Research, 2010, 23(2): 43-46 |
| [20] |
李红伟, 于文涛, 刘淑琴. 基于ANSYS的磁悬浮挠性转子模态分析与设计[J].
中国机械工程, 2014, 25(11): 1447-1452, 1459 LI Hongwei, YU Wentao, LIU Shuqin. Mode analysis and design of maglev flexible rotor with ansys[J]. China Mechanical Engineering, 2014, 25(11): 1447-1452, 1459 DOI:10.3969/j.issn.1004-132X.2014.11.006 |




