2. 山东省磁悬浮轴承工程技术研究中心, 山东 济南 250061
2. Shandong Magnetic Bearing Technology Center, Jinan 250061, Shandong, China
锂电池作为磁悬浮人工心脏泵系统的供电装置, 需要及时、准确、合理地对其进行有效管理。电池管理系统的关键技术之一是电池的荷电状态(state of charge, SOC)的估计。
目前, SOC估算方法主要有AH积分法[1-4]、放电测试法[5]、开路电压(open circuit voltage, OCV)法[6]、内阻法[7]、线性模型法、神经网络法、滑模观测法[8]及卡尔曼滤波(Kalman filter, KF)方法等。AH法与OCV法通常联合使用, 由于模型简洁, 运算量低, 易于实现, 在对电量精度要求不高的场合有着广泛应用; 文献[9]针对AH法无法确定初始电量的缺陷, 通过试验证明初始SOC值的修正方法对于提高AH法的精度最为重要。放电测试法是一种离线测量方法, 在实验室中应用较多; 内阻测量法在电池放电后期对电池的SOC估计具有较高的精度和较好的鲁棒性。为了进一步提高电池SOC估计精度, 近年来研究人员将神经网络法及扩展卡尔曼滤波等方法引入到电池的SOC预测中:文献[10]将神经网络方法应用于电动车蓄电池SOC估计, 并对3种具有代表性的神经网络方法的估计误差、噪声容忍能力进行了分析比较, 指出支持向量机网络的综合估计性能最好。文献[11-13]对锂电池的几种不同阶次的电路模型进行了参数辨识, 使用扩展卡尔曼滤波(extended Kalman filter, EKF)算法对这些模型下的电池SOC进行估算, 结果表明随着电路模型的阶次提高, EKF算法对SOC估计的误差越小。文献[14]将AH法与改进卡尔曼滤波的方法相结合, 用EKF算法对SOC初值进行收敛, 在误差范围内使用AH法对过程SOC进行估算, 降低了实时估算的复杂度。文献[15]对于二阶等效RC锂电池电路模型, 使用变遗忘因子最小二乘法辨识锂电池模型参数, 提出了基于离散H∞滤波算法的鲁棒估计法, 并进行了试验验证。文献[16]对电池的状态模型进行优化, 并提出了基于Sigma卡尔曼滤波(Sigma Kalman filter, SKF)中的无迹卡尔曼滤波(unscented Kalman filter, UKF)算法的动力电池SOC估计方法, 试验证明该方法可以快速完成SOC的精确估计, 最大误差在5%左右, 并具有一定的鲁棒性。文献[17]将文献[16]中的锂电池数学观测模型进行补偿, 考虑了松弛效应对电池电压的影响, 使用自适应Sigma卡尔曼滤波(adaptive Sigma Kalman filter, ASKF)对SOC进行估计, 最大误差在5%左右。
综合考虑现有方法的特点以及人工心脏泵的苛刻要求, 本研究依照文献[16-17]所采用的电池状态模型修正方法对磁悬浮心脏泵用锂电池状态模型进行修正, 使用UKF算法对电量初始SOC进行估计收敛; 在实时估计时, 为了快速而简便地获取精确的SOC值, 考虑了磁悬浮心脏泵工作电流小而放电变化率大的特点, 将UKF算法与AH法相结合, 并制定了该复合算法的判定策略; 最后对该复合算法的收敛速度、估计精度和复杂度进行了验证。
1 锂电池SOC估计模型电池动态系统中的状态变量除了电池SOC外, 还可以是电池的热效应能量损耗[18]、电池的可变内阻[19]等, 针对本研究研究对象电池工作的温度和不允许深度放电的特点, 所采用的电池数学模型不考虑电池的热效应能量损耗及可变内阻, 主要考虑以电池SOC作为主要的状态变量, 并考虑放电电流、端电压、工作温度与电池SOC间的关系。
1.1 状态模型电池的SOC指的是电池内所剩的容量占标称容量的百分比, 其中标称容量指电池完全充满后在室温下以标准放电速率C/30(C为额定放电电流)进行放电时所能得到的总容量。由AH法, 电池在t时刻的电量值可表示为
| $ {\rm{SOC}} = {\rm{SO}}{{\rm{C}}_0} - \frac{1}{{{Q_{\rm{N}}}}}\int_0^t {\eta \times I\left( \tau \right){\rm{d}}\tau } , $ | (1) |
式中:η为放电系数, 与放电电流、工作温度等要素有关; SOC0为电池在前一时刻的电量初值; QN为电池的标称容量; I(τ)为电池在τ时刻的即时放电电流。
为了应用卡尔曼滤波方法, 将式(1)离散变化为
| $ {\rm{SOC}}\left( {k + 1} \right) = {\rm{SOC}}\left( k \right) - \left( {\frac{{\eta \Delta t}}{{{Q_{\rm{N}}}}}} \right)I\left( k \right), $ | (2) |
式中:Δt为离散时间间隔; η为放电系数, 与放电电流、工作温度等要素有关; QN也会随着循环次数的增加而改变。本研究中考虑放电电流、工作温度、循环次数对电池电量估算的影响, 将式(2)修正为
| $ {x_{k + 1}} = {x_k} - \left( {\frac{{{\eta _i}{\eta _t}\Delta t}}{{N{Q_{\rm{N}}}}}} \right){i_k}, $ | (3) |
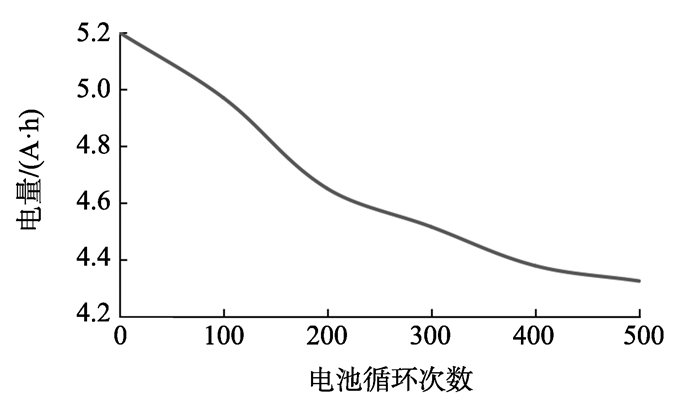
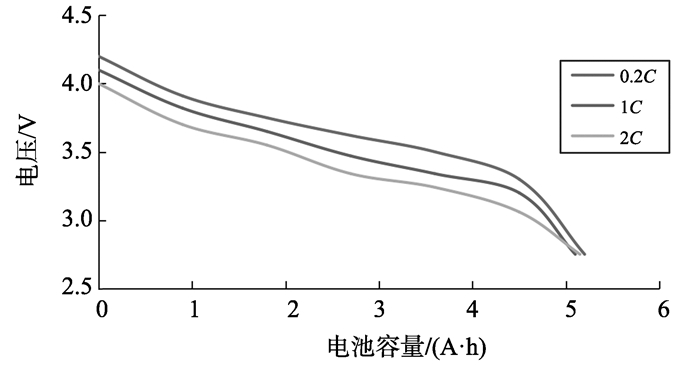
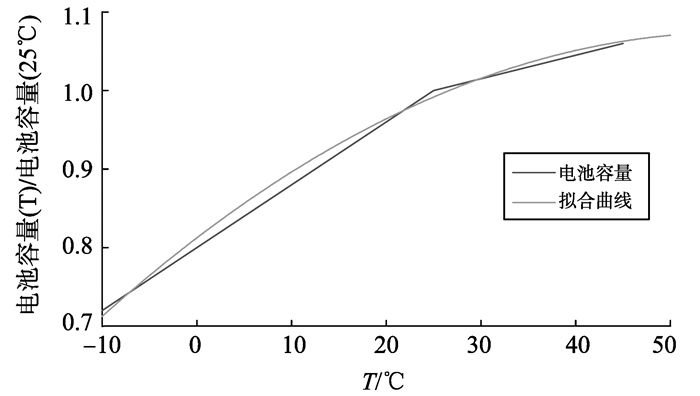
式中:N为循环次数修正因子, 用以修正不同循环次数下的电池标称容量, 使η=ηiηt, 其中ηi反映的是放电电流(效率)对电池SOC的影响程度, 即室温下放电电流为i时的放电比例系数(在标准放电速率下即i=C/30时, ηi为1);ηt反映的是电池工作温度对电池SOC的影响程度, 即工作温度为T、放电电流为C/30时的放电比例系数(在T=25 ℃时, ηt为1)。图 1为本研究中使用的三星标称容量为5.2 A·h的钴酸锂电池组循环次数和容量对应关系, 图 2和图 3分别给出了不同的放电电流和不同工作温度对电池SOC的影响程度。从图 2、3中可以看出, 在电池允许工作范围内, 随着使用次数增多, 电池满充容量逐渐下降; 电池放电速率越高, 总放电容量越低; 工作温度越高, 总放电容量越高。
|
图 1 电池容量和循环次数之间的关系图 Figure 1 The relation between the battery capacity andthe number of cycles |
|
图 2 不同放电速率下电池容量 Figure 2 Battery capacity at different discharge rates |
|
图 3 不同温度下电池容量变化 Figure 3 Variation of battery capacity at different temperatures |
关于电量估算的状态模型参数N、ηi和ηt的确定采用如下的方法:
(1) 根据电池容量在不同循环次数n下的变化, 在不同循环次数时, 通过最小二乘法在最小均方误差准则下拟合得到二次曲线Qk=an2+bn+c, 其中a, b, c为所求得的最优系数, 则在电池已循环次数n次时折算比例系数N=Qk/QN=(an2+bn+c)/QN。
(2) 根据电池在不同放电速率下所能得到的电池总容量Qk, 可知在电池以0.2C放电速率放电时, 电池的总容量几乎不变, 本研究所使用的电池为心脏泵供电电池, 最大工作电流不超过0.1C, 所以在实际工作中放电速率对于电池总容量的影响很小, 在此令ηi为1。
(3) 根据电池在不同工作温度Tk下所能得到的最终电池容量Qt, 折算成比例为Rt, 根据最小二乘法在最小均方误差准则下拟合出二次曲线Rt=dTk2+eTk+f, 其中d, e, f为所求得的最优系数, 则在温度为T时, ηt=dT2+eT+f。
1.2 观测模型常用的锂电池观测模型分为数学模型和电路模型。其中数学模型包括Shepherd模型、Unnewehr通用模型、Nernst模型和United模型[20]; 电路模型包括Rint模型、RC模型、PNGV模型和Thevenin模型[21]等。United模型整合了前述3种数学模型的优点, 在数学模型中最为贴近锂电池实际工作状态, 采用United模型作为电池观测模型, 表达式为
| $ {y_k} = {K_0} - R{i_k} - \frac{{{K_1}}}{{{x_k}}} - {K_2}{x_k} + {K_3}{\rm{Ln}}{x_k} + {K_4}{\rm{Ln}}\left( {1 - {x_k}} \right), $ | (4) |
式中:yk是电池端电压; ik是放电电流; xk是电池SOC; R是电池内阻; K1是极化电阻; K0、K2、K3和K4是常数。令上式中的模型参数为矢量θ, 则θ=[K0, R, K1, K0, K2, K3, K4], 本研究中, θ的确定可以由室温下, 以标准放电速率对电池进行一次完整放电过程中不同时刻电池端电压yk及对应的静置后电池开路电压值, 结合开路电压法, 依据最小二乘法拟合得到。
2 基于UKF和AH法的锂电池SOC复合估计 2.1 复合算法的估算步骤为了能准确估计锂电池初始SOC, 采用UKF算法使估计的电量初值SOC0迅速向初始真值收敛, 能有效解决AH法中电量初值无法确定的问题。本研究提出的基于UKF和AH法的复合估算方法, 具体估算步骤为:
第一步, 在采样初始时刻t0, 确定电量初值x0;
第二步, 在t0~tk时刻, 以x0为初值用UKF算法使电池SOC迅速向真值收敛, 在tk时刻得到电量值xk;
第三步, 在tk~tk+1时刻, 由于AH法不能准确估算电池放电变化率较大的放电情形, 采用如下策略:比较tk时刻采样电流ik与tk+1时刻采样电流ik+1, 若ik+1>2ik或ik+1 < 0.5ik, 采用UKF算法估算tk+1时刻电量xk+1, 否则, 使用式(1)的AH法估算电量xk+1, 每当电量降低10%, 重复第二步进行电量校正;
第四步, 判别当最终电量值低于10%时, 更换备用电池。
采用以上估计方法, 能充分利用UKF算法的快速收敛特性, 同时也考虑到快速变化的电流对于AH法的影响, 将UKF算法和AH法相互结合, 既能够准确估算电池SOC, 还同时降低了计算的复杂度。
2.2 复合算法实现中的UKF算法复合算法中的第二步以UKF算法为主体, 无迹卡尔曼滤波(UKF)摒弃了对非线性系函数进行线性化的传统做法, 采用卡尔曼线性滤波框架, 使用无迹变换(unscented transform, UT)处理均值和协方差的非线性传递问题, 基于迭代型最小均方误差估计对状态估计及观测估计进行更新。本算法中采用的无迹卡尔曼滤波UKF算法基本原理如图 4所示。

|
图 4 UKF算法基本原理 Figure 4 Basic principle of UKF algorithm |
将式(3)(4)中建立的电池模型分别改写为式(5)(6):
| $ {x_{k + 1}} = {x_k} - \left( {\frac{{{\eta _i}{\eta _t}\Delta t}}{{N{Q_{\rm{N}}}}}} \right){i_k} + {w_k}, $ | (5) |
| $ {y_k} = {K_0} - R{i_k} - \frac{{{K_1}}}{{{x_k}}} - {K_2}{x_k} + {K_3}{\rm{Ln}}{x_k} + {K_4}{\rm{Ln}}\left( {1 - {x_k}} \right) + {v_k}。$ | (6) |
定义处理噪声wk的协方差为Qw, 与电流ik的测量误差有关; 观测噪声vk的协方差为Rv, 与电压测量误差有关。基于式(5)(6), 采用UKF估计SOC算法实现步骤如下:
(1) 确定电池初始SOC为x0, 其估计方差为P0, 确定合适的Qw及Rv值。
(2) 考虑到处理噪声和观测噪声的影响, 将状态变量xk-1及其估计方差Pk-1分别进行如下扩展, 得到扩展状态变量Xk-1及其协方差Pk-1z为
| $ {\mathit{\boldsymbol{X}}_{k - 1}} = {\left[ {\begin{array}{*{20}{c}} {{x_{k - 1}}}&0&0 \end{array}} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{P}}_{k - 1}^z = \left[ {\begin{array}{*{20}{c}} {{P_{k - 1}}}&0&0\\ 0&{{Q_w}}&0\\ 0&0&{{R_v}} \end{array}} \right]。$ |
扩展状态变量Xk-1的维度L=3。
(3) 根据测量得到的电池端电压yk及放电电流ik, k=1, 2, …, 按照如下过程进行递推计算。
① 采用UT变换, 在Xk-1附近按照如下规则选取2L+1个Sigma点
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{X}}^{\left( 0 \right)}} = \mathit{\boldsymbol{\bar X}},i = 0\\ {\mathit{\boldsymbol{X}}^{\left( i \right)}} = \mathit{\boldsymbol{\bar X}} + {\left( {\sqrt {\mathit{\boldsymbol{P}}\left( {L + \lambda } \right)} } \right)_i},i = 1 \sim L\\ {\mathit{\boldsymbol{X}}^{\left( i \right)}} = \mathit{\boldsymbol{\bar X}} - {\left( {\sqrt {\mathit{\boldsymbol{P}}\left( {L + \lambda } \right)} } \right)_i},i = L + 1 \sim 2L \end{array} \right., $ | (7) |
式中:(
这些采样点的均值和协方差等于原状态分布的均值和协方差, 其加权系数为
| $ \left\{ \begin{array}{l} w_{\rm{m}}^{\left( 0 \right)} = \frac{\lambda }{{L + \lambda }}\\ w_{\rm{c}}^{\left( 0 \right)} = \frac{\lambda }{{L + \lambda }} + \left( {1 - {\alpha ^2} + \beta } \right)\\ w_{\rm{m}}^{\left( i \right)} = w_{\rm{c}}^{\left( i \right)} = \frac{1}{{2\left( {L + \lambda } \right)}},i = 1 \sim 2L \end{array} \right., $ |
式中:下标m为均值; c为协方差; 上标i为第i个采样点; 参数λ=α2(L+ε)-L是一个缩放比例参数, 用以降低总的预测误差, α的选取控制了采样点的分布状态, 一般取值为0~1, 这里取0.01, ε是待选参数, 取值通常应确保矩阵P(L+λ)为半正定矩阵。
利用式(7)获得sigma点集
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}^{\left( i \right)}}\left( {k\left| k \right.} \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}\left( {k\left| k \right.} \right)}&{\mathit{\boldsymbol{\hat X}}\left( {k\left| k \right.} \right) + \sqrt {\left( {L + \lambda } \right)\mathit{\boldsymbol{P}}\left( {k\left| k \right.} \right)} } \end{array}} \right.}\\ {\left. {\mathit{\boldsymbol{\hat X}}\left( {k\left| k \right.} \right) - \sqrt {\left( {L + \lambda } \right)\mathit{\boldsymbol{P}}\left( {k\left| k \right.} \right)} } \right]。} \end{array} $ |
② 根据状态方程进行状态更新
由式(5)计算2L+1个Sigma点集的一步预测
| $ {\mathit{\boldsymbol{X}}^{\left( i \right)}}\left( {k + 1\left| k \right.} \right) = F\left[ {k,{\mathit{\boldsymbol{X}}^{\left( i \right)}}\left( {k\left| k \right.} \right)} \right],i = 1,2, \cdots ,2L + 1。$ |
对预测值进行加权求均值并求得预测均方差
| $ \mathit{\boldsymbol{\hat X}}\left( {k + 1\left| k \right.} \right) = \sum\limits_{i = 0}^{2L} {w_m^{\left( i \right)}{\mathit{\boldsymbol{X}}^{\left( i \right)}}\left( {k + 1\left| k \right.} \right)} 。$ |
求得预测均方差:
| $ \begin{array}{l} \mathit{\boldsymbol{P}}\left( {k + 1\left| k \right.} \right) = \\ \;\;\;\;\;\;\;\sum\limits_{i = 0}^{2L} {w_{\rm{c}}^{\left( i \right)}\left[ {\mathit{\boldsymbol{\hat X}}\left( {k + 1\left| k \right.} \right) - {\mathit{\boldsymbol{X}}^{\left( i \right)}}\left( {k + 1\left| k \right.} \right)} \right]} \\ \;\;\;\;\;\;\;{\left[ {\mathit{\boldsymbol{\hat X}}\left( {k + 1\left| k \right.} \right) - {\mathit{\boldsymbol{X}}^{\left( i \right)}}\left( {k + 1\left| k \right.} \right)} \right]^{\rm{T}}} + {Q_{wk}}Q_{wk}^{\rm{T}}。\end{array} $ |
根据一步预测值, 再次使用UT变换, 产生新的Sigma点集
| $ \begin{array}{l} {\mathit{\boldsymbol{X}}^{\left( i \right)}}\left( {k + 1\left| k \right.} \right) = \left[ {\mathit{\boldsymbol{\hat X}}\left( {k + 1\left| k \right.} \right)\;\;\;\;\mathit{\boldsymbol{\hat X}}\left( {k + 1\left| k \right.} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\sqrt {\left( {L + \lambda } \right)\mathit{\boldsymbol{P}}\left( {k + 1\left| k \right.} \right)} \mathit{\boldsymbol{\hat X}}\left( {k + 1\left| k \right.} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\left. {\sqrt {\left( {L + \lambda } \right)\mathit{\boldsymbol{P}}\left( {k + 1\left| k \right.} \right)} } \right]。\end{array} $ |
③ 根据观测方程进行测量更新
将②中Sigma点集代入观测方程, 得到预测的Sigma观测点集
| $ \begin{array}{*{20}{c}} {{y^{\left( i \right)}}\left( {k + 1\left| k \right.} \right) = \mathit{\boldsymbol{H}}\left[ {{\mathit{\boldsymbol{X}}^{\left( i \right)}}\left( {k + 1\left| k \right.} \right)} \right],}\\ {i = 1,2, \cdots ,2L + 1。} \end{array} $ |
求得观测点集的均值
| $ \bar y\left( {k + 1\left| k \right.} \right) = \sum\limits_{i = 0}^{2L} {w_m^{\left( i \right)}{y^{\left( i \right)}}\left( {k + 1\left| k \right.} \right)} 。$ |
求得观测点集的方差Pykyk和Pxkyk:
| $ \begin{array}{l} {P_{{y_k}{y_k}}} = \sum\limits_{i = 0}^{2L} {w_c^{\left( i \right)}\left[ {\hat y\left( {k + 1\left| k \right.} \right) - {y^{\left( i \right)}}\left( {k + 1\left| k \right.} \right)} \right]} \\ \;\;\;\;\;\;\;\;\;\;{\left[ {\hat y\left( {k + 1\left| k \right.} \right) - {y^{\left( i \right)}}\left( {k + 1\left| k \right.} \right)} \right]^{ - 1}} + {R_v}, \end{array} $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{P}}_{{x_k}{y_k}}} = \sum\limits_{i = 0}^{2L} {w_c^{\left( i \right)}\left[ {\mathit{\boldsymbol{\hat X}}\left( {k + 1\left| k \right.} \right) - {\mathit{\boldsymbol{X}}^{\left( i \right)}}\left( {k + 1\left| k \right.} \right)} \right]} \\ \;\;\;\;\;\;\;\;\;\;{\left[ {\hat y\left( {k + 1\left| k \right.} \right) - {y^{\left( i \right)}}\left( {k + 1\left| k \right.} \right)} \right]^{ - 1}}。\end{array} $ |
计算系统的Kalman增益矩阵以及系统的状态更新和协方差更新
| $ \mathit{\boldsymbol{K}}\left( {k + 1} \right) = {\mathit{\boldsymbol{P}}_{{x_k}{y_k}}}P_{{y_k}{y_k}}^{ - 1}。$ |
系统的状态更新
| $ \begin{array}{l} \mathit{\boldsymbol{\hat X}}\left( {k + 1\left| {k + 1} \right.} \right) = \mathit{\boldsymbol{\hat X}}\left( {k + 1\left| k \right.} \right) + \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{K}}\left( {k + 1} \right)\left[ {y\left( {k + 1} \right) - \bar y\left( {k + 1\left| k \right.} \right)} \right]。\end{array} $ |
系统的协方差更新
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}}\left( {k + 1\left| {k + 1} \right.} \right) = \mathit{\boldsymbol{P}}\left( {k + 1\left| k \right.} \right) - }\\ {\mathit{\boldsymbol{K}}\left( {k + 1} \right){P_{{y_k}{y_k}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\left( {k + 1} \right)。} \end{array} $ |
按照上述迭代过程得到的更新状态
根据电池初始放电电流及端电压, 应用UKF算法进行心脏泵用锂电池的SOC初值收敛并完成整个电量估算过程, 收敛过程与误差曲线如图 5所示。收敛过程采取了前100 s采样周期的估算值, 误差曲线针对于电量值10%~100%时间段。

|
图 5 UKF算法进行SOC估计 Figure 5 UKF algorithm for SOC estimation |
依据前文所提出电量估算状态模型参数N, ηi和ηt的确定方法,通过试验获得所使用的参数为:
| $ \begin{array}{l} \mathit{\boldsymbol{\theta }} = \left[ {\begin{array}{*{20}{c}} {21.2593}&{0.0832}&{0.6389}&{ - 4.5732} \end{array}} \right.\\ \;\;\;\;\;\;\;\;\left. {\begin{array}{*{20}{c}} { - 1.8732}&{ - 0.035\;34} \end{array}} \right], \end{array} $ |
| $ \left[ {\begin{array}{*{20}{c}} a&b&c \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {5.6 \times {{10}^{ - 7}}}&{ - 6.3 \times {{10}^{ - 4}}}&1 \end{array}} \right], $ |
| $ \left[ {\begin{array}{*{20}{c}} d&e&f \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 4.2 \times {{10}^{ - 5}}}&{0.0\;048}&{0.9} \end{array}} \right]。$ |
电池SOC的初始估计方差P0的选择直接影响算法的响应速度[16]。算法的收敛速度与P0的取值呈正线性关系, 通常取值范围在0.1~10。令P0取值为0.1, 初始电量估计值x0为0.8, 处理噪声wk方差Qw为10-6, 观测噪声vk方差Rv为10-2。
从图 5中可看出真实SOC的值为1, 虽然算法选定的初始SOC值x0为0.8, 两者存在一定偏差, 但UKF算法能快速地跟踪上真实SOC值。表 1给出了UKF算法的性能参数。
| 表 1 误差与收敛时间 Table 1 Calculation error and convergence time |
当本研究选用的初始SOC值x0不同时, 收敛时间也不同, 具体计算结果见表 2。
| 表 2 不同电量初值x0的收敛时间 Table 2 Convergence time under different initial values x0 of SOC |
由表 2可知, 初始电量x0误差越大, UKF算法自身收敛的速度也随着增加, 但还保持了快速收敛特性, 能很好地解决AH法无法估计初始SOC值的问题。
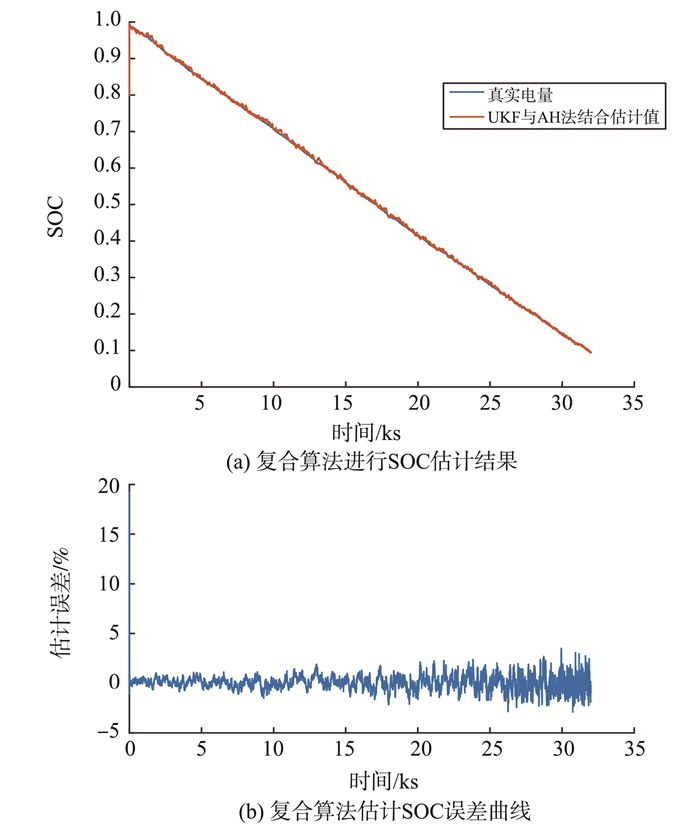
3.2 复合算法估计结果应用基于UKF和AH法的锂电池SOC复合估计策略, 将tk-t0差值设定为10 s, 每更换两次电池, 循环次数n增加1, 当初始电量x0为0.8时, 应用此复合算法, 估算结果见图 6。
|
图 6 复合算法估计结果 Figure 6 Estimation results of the compound algorithm |
由图 6中误差曲线可知, 采用该复合算法对磁悬浮心脏泵用锂电池进行电量估计, 最大估计误差为4.036 2%。与单纯使用UKF算法相比, 误差基本相同, 由于部分估算过程由AH法代替UKF算法完成, 该复合算法能大大降低计算的复杂度。
4 试验分析试验数据通过锂电池试验平台获得, 试验平台由可变负载、锂电池组及保护模块、数据采集装置等组成, 试验中测试所用电池为三星18 650组装锂电池, 电压24 V, 标称容量为5.2 A·h。使用高精度电压、电流测量仪器记录锂电池的工作电压和电流, 采样频率为1 Hz。
图 7显示的是测试过程中获得的电压、电流, 测试过程中电池温度基本保持室温不变。从图 7(a)中可以看出, 电池的放电电流在1 A以内变化。图 7(b)显示电压的线性范围是从放电开始的电压25 V到22 V基本呈线性下降, 之后则快速下降。

|
图 7 锂电池的放电电流、端电压 Figure 7 Discharge current and terminal voltage oflithium batteries |
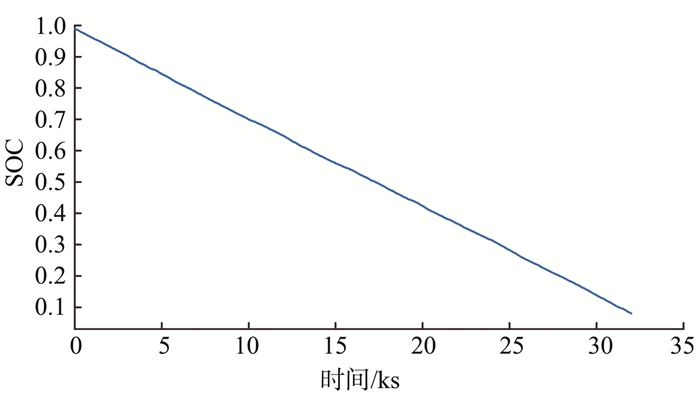
图 8中放电过程中各个时刻的SOC数值是通过计算锂电池放电到截止电压时所释放的总电量, 然后用此总电量作为基准计算得到的。
|
图 8 锂电池实际SOC Figure 8 Actual SOC of lithium batteries |
本研究通过UKF算法和AH法结合的复合算法对心脏泵用锂电池的电量进行了估算, 并进行了试验验证, 结果表明:
(1) 复合算法可快速精准地估计锂电池SOC, 估计误差约为4%, 与单纯使用UKF算法相比, 虽然估计误差几乎相同, 但是计算复杂度大大降低, 适合实时在线计算。
(2) 修正磁悬浮心脏泵用锂电池的状态模型和数学观测模型适合于锂电池的精确估算, 在应用中应主要考虑电池循环次数和工作温度的影响。
(3) 要精确给出电量的初始值是困难的, 复合算法不依赖精确的初始值就能实现初始电量估值向真实值的快速收敛。
| [1] |
林成涛, 陈全世, 王军平, 等. 用改进的安时计量法估计电动汽车动力电池SOC[J].
清华大学学报(自然科学版), 2006, 46(2): 247-251 LIN Chengtao, CHEN Quanshi, WANG Junping, et al. Improved Ah counting method for state of charge estimation of electric vehicle batteries[J]. Journal of Tsinghua University(Science and Technology), 2006, 46(2): 247-251 |
| [2] |
于海芳, 逯仁贵, 朱春波, 等. 基于安时法的镍氢电池SOC估计误差校正[J].
电工技术学报, 2012, 27(6): 12-18 YU Haifang, LU Rengui, ZHU Chunbo, et al. State of charge estimation calibration for Ni-MH battery based on ampere-hour method[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 12-18 |
| [3] |
郏航. 电动汽车电池电量监测系统的研究与实现[D]. 北京: 清华大学, 1996.
JIA Hang. Research and implementation of battery monitoring system for electric vehicle[D]. Beijing: Tsinghua University, 1996. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y206255 |
| [4] |
鲍慧, 于洋. 基于安时积分法的电池SOC估算误差校正[J].
计算机仿真, 2013, 30(11): 148-159 BAO Hui, YU Yang. State of charge estimation calibratio based on ampere-hour method[J]. Computer Simulation, 2013, 30(11): 148-159 DOI:10.3969/j.issn.1006-9348.2013.11.033 |
| [5] |
林成涛, 王军平, 陈全世. 电动汽车SOC估计方法原理与应用[J].
电池, 2004, 34(5): 376-378 LIN Chengtao, WANG Junping, CHEN Quanshi. Methods for state of charge estimation of EV batteries and their application[J]. Battery Bimonthly, 2004, 34(5): 376-378 |
| [6] | HE H, ZHANG X, XIONG R, et al. Online model-based estimation of state-of-charge and open-circuit voltage of lithiumion batteries in electric vehicles[J]. Energy, 2012, 39(1): 310-318 DOI:10.1016/j.energy.2012.01.009 |
| [7] |
李革臣, 古艳磊. 电化学阻抗谱法预测锂电池荷电状态[J].
电源技术, 2008, 32(9): 599-602 LI Gechen, GU Yanlei. SOC of lithiumion rechargeable battery predicted by electrochemical impedance spectronscopy[J]. Chinese Journal of Power Source, 2008, 32(9): 599-602 |
| [8] |
孙冬, 陈息坤. 基于离散滑模观测器的锂电池荷电状态估计[J].
中国电机工程学报, 2015, 35(1): 185-191 SUN Dong, CHEN Xikun. Charge state estimation of Li-ion batteries based on discrete-time sliding mode observers[J]. Proceedings of the CSEE, 2015, 35(1): 185-191 |
| [9] |
李哲, 卢兰光, 欧阳明高. 提高安时积分法估算电池SOC精度的方法比较[J].
清华大学学报(自然科学版), 2010(8): 1293-1296 LI Zhe, LU Languang, OUYANG Minggao. Comparison of methods for improving SOC estimation accuracy through an ampere-hour integeration approach[J]. Journal of Tsinghua University(Science and Technology), 2010(8): 1293-1296 |
| [10] |
雷肖, 陈清泉, 刘开培, 等. 电动车蓄电池荷电状态估计的神经网络方法[J].
电工技术学报, 2007, 22(8): 150-160 LEI Xiao, CHEN Qingquan, LIU Kaipei, et al. Battery state of charge estimation based on neural-network for electric vehicles[J]. Transactions of China Electrotechnical Society, 2007, 22(8): 150-160 |
| [11] |
刘浩. 基于EKF的电动汽车用锂离子电池SOC估算方法研究[D]. 北京: 北京交通大学, 2010.
LIU Hao. Study on SOC estimation method of lithium-ion battery based on EKF for electric vehicles[D]. Beijing: Beijing Jiaotong University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10004-2010119815.htm |
| [12] |
袁学庆, 张阳, 赵林, 等. 基于EKF的锂电池SOC估算与试验研究[J].
电源技术, 2015, 39(12): 2587-2589 YUAN Xueqing, ZHANG Yang, ZHAO Lin, et al. Li-ion battery SOC estimation and test research based on EKF[J]. Chinese Journal of Power Source, 2015, 39(12): 2587-2589 DOI:10.3969/j.issn.1002-087X.2015.12.009 |
| [13] |
冯光. 基于EKF的锂离子电池SOC估算的建模与仿真[D]. 武汉: 武汉理工大学, 2013.
FENG Guang. Modeling and simulation based on EKF lithium-ion battery SOC estimation[D]. Wuhan: Wuhan University of Technology, 2013. http://www.doc88.com/p-1075432261286.html |
| [14] |
李建成, 戴瑜兴, 全惠敏, 等. 基于改进Kalman滤波和安时积分的SOC复合估算[J].
电源技术, 2014(12): 2267-2269 LI Jiancheng, DAI Yuxing, QUAN Huimin, et al. SOC estimating method based on improved Kalman filter and AH integrator[J]. Chinese Journal of Power Source, 2014(12): 2267-2269 DOI:10.3969/j.issn.1002-087X.2014.12.034 |
| [15] |
陈息坤, 孙冬, 陈小虎. 锂离子电池建模及其荷电状态鲁棒估计[J].
电工技术学报, 2015, 30(15): 141-147 CHEN Xikun, SUN Dong, CHEN Xiaohu. Modeling and state of charge robust estimation for lithium-ion batteries[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 141-147 DOI:10.3969/j.issn.1000-6753.2015.15.016 |
| [16] |
高明煜, 何志伟, 徐杰. 基于采样点卡尔曼滤波的动力电池SOC估计[J].
电工技术学报, 2011, 26(11): 161-167 GAO Mingyu, HE Zhiwei, XU Jie. Sigma point Kalman filter based SOC estimation for power supply battery[J]. Transactions of China Electrotechnical Society, 2011, 26(11): 161-167 |
| [17] |
刘毅, 谭国俊, 何晓群. 优化电池模型的自适应Sigma卡尔曼荷电状态估算[J].
电工技术学报, 2017, 32(2): 108-118 LIU Yi, TAN Guojun, HE Xiaoqun. Optimized battery model based adaptive Sigma Kalman filter for state of charge estimation[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 108-118 |
| [18] |
刘金枝, 杨鹏, 李练兵. 一种基于能量建模的锂离子电池电量估算方法[J].
电工技术学报, 2015, 30(13): 100-107 LIU Jinzhi, YANG Peng, LI Lianbing. A method to estimate the capacity of the lithium-ion battery based on energy model[J]. Transactions of China Electrotechnical Society, 2015, 30(13): 100-107 DOI:10.3969/j.issn.1000-6753.2015.13.014 |
| [19] |
刘新天, 何耀, 曾国建, 等. 考虑温度影响的锂电池功率状态估计[J].
电工技术学报, 2016, 31(13): 155-163 LIU Xintian, HE Yao, ZENG Guojian, et al. State-of-power estimation for li-ion battery considering the effect of temperature[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 155-163 DOI:10.3969/j.issn.1000-6753.2016.13.018 |
| [20] | LI J, BARILLAS J K, GUENTHER C, et al. A comparative study of state of charge estimation algorithms for LiFePO4, batteries used in electric vehicles[J]. Journal of Power Source, 2013, 230(10): 244-250 |
| [21] | SEAMAN A, MCPHEE J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation[J]. Journal of Power Sources, 2014, 256(3): 410-423 |




