2. 山东省磁悬浮轴承工程技术研究中心,山东 济南 250061
2. Shandong Magnetic Bearing Technology Center, Jinan 250061, Shandong, China
磁悬浮平台悬挂铁块运行时会出现铁块单摆振荡的现象,表明系统在受到某种干扰时,系统的阻尼无法使系统恢复稳定状态。系统的阻尼系数受频率等外界因素的影响较大。分析可知,要得到系统发生振荡时的阻尼系数需要平台垂直方向上的速度v与加速度a信息。在一般的磁悬浮控制系统中,悬浮气隙信号通过位移传感器获得,加速度信号由加速度计获得,速度信号不能直接获得。而实际悬浮控制系统中,由加速度计所获得的加速度信号含有较大噪声干扰,难以直接利用, 故构造状态观测器,根据磁极悬浮间隙估算速度信号和加速度信号。状态观测器[1],是一个在物理上可以实现的动态系统,利用待观测系统的可以测量得到的输入和输出信息来估计待观测系统的状态变量,以便用该组状态变量的估计值来代替待观测系统的真实状态变量。20世纪60年代初期,为了对控制系统实现状态反馈或其他需要,文献[1]提出状态观测器的概念和构造方法,通过重构途径解决状态不能直接量测的问题。状态观测器的出现,不但为状态反馈的技术实现提供实际可能性,而且在控制工程的许多方面也得到实际应用。文献[2]在永磁同步发电机当中根据定子侧电流、电压利用观测器估算出磁场定向控制所需要的位置信息和转速控制器的输入反馈转速信息。文献[3]在倒立摆中设计状态观测器估计车体速度和摆杆角速度变量。文献[4]在航天控制中使用状态观测器观测运载火箭的姿态角速度。文献[5]利用干扰观测器估计开关功率放大器的延时扰动。本研究为了获得平台垂直方向上的速度与加速度的估计值,在控制系统中引入了状态观测器。首先根据磁极的受力分析与线圈的回路电压分析计算构筑被控磁极的状态方程,在此基础上设计状态观测器,并且为了保持原系统鲁棒性不变,对加入观测器的系统进行极点配置。
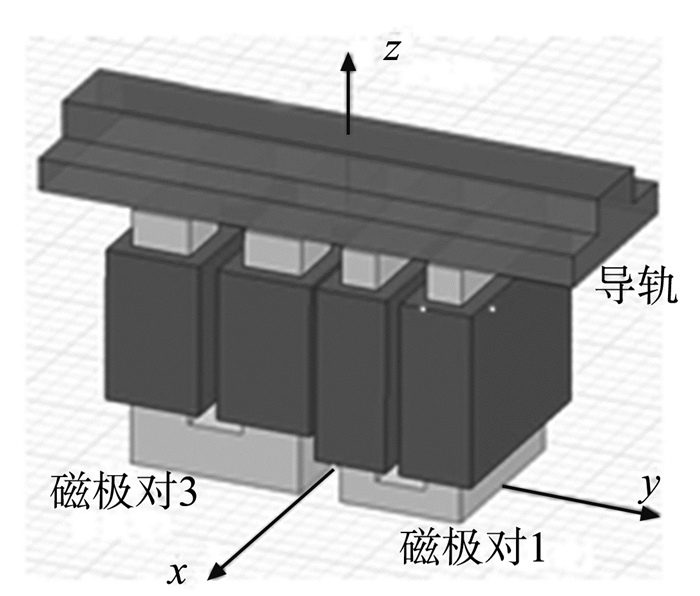
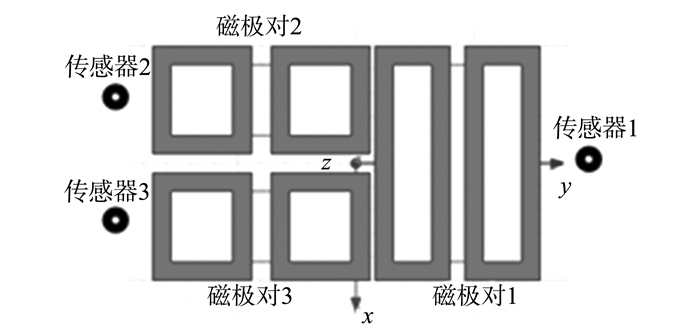
1 磁悬浮平台悬挂铁块运行时的单摆振荡现象 1.1 悬浮系统的单摆振荡问题本研究中的磁悬浮直线运动平台需要进行10 m以上的直线运动。图 1是包括导轨在内的平台的结构示意图,平台共有3对磁极,其中磁极对2与3关于导轨对称。图 2是磁极的分布图。3对磁极配合解决磁悬浮平台的运行中的俯仰和摇摆问题。
|
图 1 直线平台结构示意图 Figure 1 The sketch map of linear platform structure |
|
图 2 磁极分布示意图 Figure 2 Schematic diagram of magnetic pole distribution |
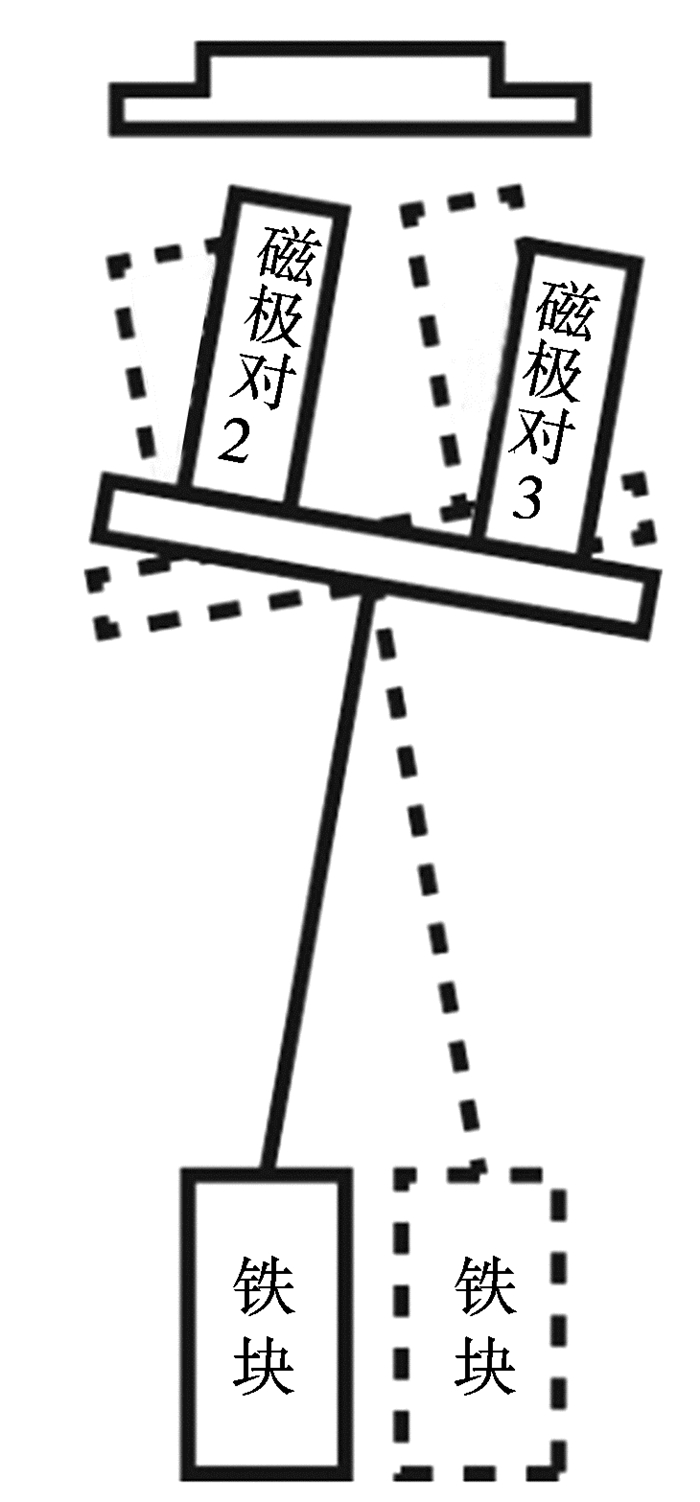
本研究采用鲁棒性比较强的PID控制算法,但是按照常规的控制稳定域设计控制器,磁悬浮直线运动平台在稳定悬浮一定时间后会出现绕y轴低频扰动(钟摆现象),摆动的幅度从开始的很小逐渐变大,直至系统失稳见图 3。
|
图 3 小平台下的单摆振荡 Figure 3 The simple pendulum oscillation on a small platform |
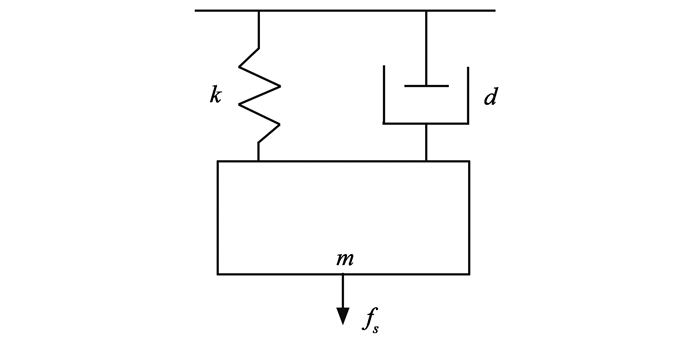
针对上述悬浮系统的单摆振荡问题,如果磁悬浮系统的阻尼为正,则在受扰动影响出现振荡时,摇摆的幅度会逐渐变小直至系统趋于稳定。但本研究中摇摆的幅度从开始的很小逐渐变大,表明此时阻尼系数应为负。为了确切得到阻尼系数值,将单自由度磁悬浮系统与单质量弹簧阻尼系统作比较,图 4所示是由质量、弹簧、阻尼器组成的单质量弹簧阻尼系统。
|
图 4 单质量弹簧阻尼系统 Figure 4 The single mass spring damping system |
外作用力为fs。设质量m相对于初始状态的位移、速度和加速度分别为sd、v和a,由牛顿第二定律可得
| $ {f_s} - k{s_{\rm{d}}} - dv = ma, $ | (1) |
式中:k是刚度系数,d是阻尼系数。根据文献[6]可知,由于刚度系数k与PID控制中的积分环节无关,而且系统微分环节延时较小,所以刚度系数k受到干扰频率等因素的影响较少,这里可以将刚度系数k看作固定值。
由式(1)可得阻尼系数d的定义式为
| $ d = \frac{{{f_s} - k{s_{\rm{d}}} - ma}}{v}, $ | (2) |
由式(2)可知,要得到阻尼系数d必须首先知道磁极的速度和加速度,但在磁悬浮控制系统中,气隙信号通过位移传感器获得,加速度信号即时由加速度计获得,但是速度信号不能直接获得。并且实际悬浮控制系统中,加速度计获取的加速度信号往往含有较大噪声,难以利用。故采用设计状态观测器的方法,根据气隙信号估计速度信号和加速度信号。
2 磁极的状态方程构造状态观测器需要系统的状态方程。本研究中待求的状态变量为磁极垂直方向上的速度
本研究设计的磁悬浮平台的执行装置包含了3个电磁铁,采用分散控制,每个电磁铁由一套独立的磁悬浮控制电路控制,因此受力分析可以对每个电磁铁单独进行分析计算。每个执行电磁铁均为U型电磁铁,假设磁通均沿着铁芯磁路,忽略漏磁现象和边缘效应[7],简化模型见图 5。
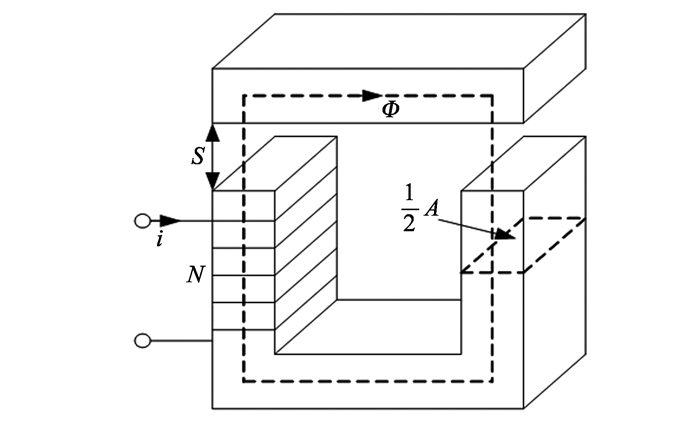
|
图 5 U型电磁铁模型 Figure 5 The model of U-type electro-magnet |
图 5中A为有效磁极面积, m2; N为线圈匝数; I为线圈电流,A; S为悬浮间隙,m; ϕ为磁通量,Wb。
磁极电磁力的计算公式为
| $ f = \frac{1}{4}{u_0}{N^2}A\frac{{{i^2}}}{{{S^2}}}, $ | (3) |
式中μ0为真空磁导率。电磁力与线圈电流的平方成正比,与气隙长度的平方成反比,可以看出磁悬浮平台是一个非线性系统。
在平台稳定悬浮时,电磁铁产生的电磁力与平台自身重力相等,因此
| $ f = \frac{1}{4}{u_0}{N^2}A\frac{{I_0^2}}{{S_0^2}} = mg, $ | (4) |
式中:I0为额定线圈电流,A; S0为额定气隙长度,m。当平台在平衡位置处受到小位移干扰时,出现位移量为sd; 电流变化量为i, 则电磁力
| $ f = \frac{1}{4}{u_0}{N^2}A\frac{{{{\left( {{I_0} + i} \right)}^2}}}{{{{\left( {{S_0} + {s_{\rm{d}}}} \right)}^2}}}。$ | (5) |
将式(3)在i=0, sd=0处进行泰勒展开,对系统在平衡位置附近进行线性化并略去二阶以上的量得到电磁力的表达式为
| $ f = {f_0} + \frac{{\partial f}}{{\partial {s_{\rm{d}}}}}{s_{\rm{d}}} + \frac{{\partial f}}{{\partial i}}i = {f_0} - {k_{{\rm{ss}}}}{s_{\rm{d}}} + {k_{{\rm{si}}}}i, $ | (6) |
式中:定义kss为位移刚度系数,ksi为电流刚度系数
| $ {k_{{\rm{ss}}}} = \frac{{{\mu _0}{N^2}AI_0^2}}{{2S_0^3}}, $ | (7) |
| $ {k_{{\rm{si}}}} = \frac{{{\mu _0}{N^2}A{I_0}}}{{2S_0^2}}。$ | (8) |
磁极的受力方程为
| $ ma = {k_{{\rm{ss}}}}{s_{\rm{d}}} - {k_{{\rm{si}}}}。$ | (9) |
根据电路理论,电磁铁线圈回路电压方程[7]为
| $ U = i{R_{\rm{L}}} + L\frac{{{\rm{d}}i}}{{{\rm{d}}t}} + i\frac{{{\rm{d}}L}}{{{\rm{d}}t}}, $ | (10) |
式中:RL为线圈电阻,Ω; L为线圈电感,H。电感系数L与线圈的匝数和构成磁路的磁阻有关,当忽略铁芯磁阻时,电感
| $ L = \frac{{{u_0}{N^2}A}}{{2S_0^2}}。$ | (11) |
当平台在稳定悬浮状态下出现微小位移s时,将式(11)代入式(10)中,线圈两端电压为
| $ \begin{array}{l} U' = \left( {{I_0} + i} \right){R_{\rm{L}}} + L\frac{{{\rm{d}}\left( {{I_0} + i} \right)}}{{{\rm{d}}t}} + \left( {{I_0} + i} \right)\frac{{{\rm{d}}L}}{{{\rm{d}}t}} = \\ \;\;\;\left( {{I_0} + i} \right){R_{\rm{L}}} + \frac{{{u_0}{N^2}A}}{{2\left( {{S_0} + {s_{\rm{d}}}} \right)}}\frac{{{\rm{d}}i}}{{{\rm{d}}t}} + \frac{{{u_0}{N^2}A}}{{2{{\left( {{S_0} + {s_{\rm{d}}}} \right)}^2}}}\left( {{I_0} + i} \right)\frac{{{\rm{d}}{s_{\rm{d}}}}}{{{\rm{d}}t}}, \end{array} $ | (12) |
当发生微小位移s时,线圈的端电压可以表示为额定电压加控制电压U′=U+u, 此时控制器施加的控制电压
| $ u \approx i{R_{\rm{L}}} + \frac{{{u_0}{N^2}A}}{{2{S_0}}}\frac{{{\rm{d}}i}}{{{\rm{d}}t}} + \frac{{{u_0}{N^2}A}}{{2S_0^2}}{I_0}\frac{{{\rm{d}}{s_{\rm{d}}}}}{{{\rm{d}}t}}, $ | (13) |
式(13)可以简化为
| $ u = i{R_{\rm{L}}} + L\frac{{{\rm{d}}i}}{{{\rm{d}}t}} - {k_{{\rm{si}}}}\frac{{{\rm{d}}{s_{\rm{d}}}}}{{{\rm{d}}t}}。$ | (14) |
将式(9)与式(14)两个公式联立构成的微分方程组即为系统的状态方程。
3 状态观测器的设计 3.1 3维状态方程的矢量矩阵形式首先构筑以控制电压u为输入,(sd,v,a)为状态变量的3维状态观测器。根据式(9)与式(14)构筑状态方程[1]
| $ \left\{ \begin{array}{l} ma = {k_{{\rm{ss}}}}{s_{\rm{d}}} - {k_{{\rm{si}}}}i,\\ u = i{R_{\rm{L}}} + Li - {k_{{\rm{si}}}}v, \end{array} \right. $ | (15) |
将式(15)写成矢量矩阵的形势,则状态方程变为
| $ \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{s_{\rm{d}}}}\\ v\\ a \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&1\\ {\frac{{{k_{{\rm{ss}}}}{R_{\rm{L}}}}}{{mL}}}&0&{ - \frac{{{R_{\rm{L}}}}}{L}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{s_{\rm{d}}}}\\ v\\ a \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ { - \frac{{{k_{{\rm{si}}}}}}{{mL}}} \end{array}} \right]\mathit{\boldsymbol{u}}}\\ {\mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{s_{\rm{d}}}}\\ v\\ a \end{array}} \right]} \end{array}} \right.。$ | (16) |
式中:u=[u], Y=[sd]。
3.2 用降维观测器重构由于状态分量s可由Y直接提供,其余的两个状态分量v、a只需用2维的降维观测器重构即可。这里将式(16)调整为
| $ \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\dot v}\\ {\dot a}\\ {{{\dot s}_{\rm{d}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&{ - \frac{{{R_{\rm{L}}}}}{L}}&{\frac{{{k_{{\rm{ss}}}}{R_{\rm{L}}}}}{{mL}}}\\ 1&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} v\\ a\\ {{s_{\rm{d}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ { - \frac{{{k_{{\rm{si}}}}}}{{mL}}}\\ 0 \end{array}} \right]\mathit{\boldsymbol{u}}}\\ {\mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} v\\ a\\ {{s_{\rm{d}}}} \end{array}} \right]} \end{array}} \right., $ | (17) |
然后设观测增益矩阵为G=[g1 g2],令(v,a)为x1, 将式(17)中的矩阵进行分割,令
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot w}} = \left[ {\left( {{\mathit{\boldsymbol{A}}_{11}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{A}}_{21}}} \right)\mathit{\boldsymbol{G + }}\left( {{\mathit{\boldsymbol{A}}_{12}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{A}}_{22}}} \right)} \right]\mathit{\boldsymbol{y}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\mathit{\boldsymbol{A}}_{11}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{A}}_{21}}} \right)\mathit{\boldsymbol{w}} + \left( {{\mathit{\boldsymbol{B}}_1} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{B}}_2}} \right)\mathit{\boldsymbol{u}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{x}}_1} = \mathit{\boldsymbol{w}} + \mathit{\boldsymbol{Gy}} \end{array} \right., $ | (18) |
将对应的矩阵代入到式(18)得到的二维观测器为
| $ \left\{ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{{\dot w}_1}}\\ {{{\dot w}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {g_1}}&1\\ { - {g_2}}&{ - \frac{{{R_{\rm{L}}}}}{L}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{w_1}}\\ {{w_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ { - \frac{{{k_{{\rm{si}}}}}}{{mL}}} \end{array}} \right]\mathit{\boldsymbol{u}} + \\ \;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} { - g_1^2 + {g_2}}\\ { - {g_1}{g_2} - \frac{{{R_{\rm{L}}}}}{L} + \frac{{{k_{{\rm{ss}}}}R}}{{mL}}} \end{array}} \right]\mathit{\boldsymbol{y}}\\ \left[ {\begin{array}{*{20}{c}} v\\ a \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{w_1}}\\ {{w_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{g_1}}\\ {{g_2}} \end{array}} \right]\mathit{\boldsymbol{y}} \end{array} \right.。$ | (19) |
根据文献[8]可知,磁悬浮PID控制系统系统的特征方程为
| $ m{s^2} + {k_{{\rm{si}}}}{k_{\rm{d}}}{A_{\rm{a}}}{A_{\rm{s}}}s + {k_{{\rm{si}}}}{k_{\rm{p}}}{A_{\rm{a}}}{A_{\rm{s}}} + {k_{{\rm{ss}}}} = 0, $ | (20) |
本研究的磁悬浮平台中,悬浮质量m=7 kg,功放增益Aa=1,传感器增益As=10 000,微分增益kd=0.003 9,比例增益kp=1.678 6。计算式(20)中的2阶方程可得原本的PID控制系统的极值点为s1、2=388.7±j388.7。
系统极值点在复平面上的位置见图 6,x轴为实轴,y轴为虚轴。原系统的阻尼角45°,此时系统的阻尼比

|
图 6 复平面上的特征根 Figure 6 Characteristic roots on complex planes |
由于系统的阻尼比影响系统的响应时间和超调量,为了不影响系统的动态性能,保持加入观测器后阻尼角45°不变[9-14]。根据文献[7]可知观测器的响应要快于系统的响应速度,则观测器的闭环极点需要离虚轴更远。观测器的极点值可以取λ1、2=400±j400。
由
将g1、g2代入到式(19)中可得:
| $ \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{\dot w}_1}}\\ {{{\dot w}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 728.5}&1\\ { - 268{\rm{k}}}&{ - 71.42} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{w_1}}\\ {{w_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ { - 238} \end{array}} \right]\mathit{\boldsymbol{u}} + }\\ {\left[ {\begin{array}{*{20}{c}} { - 262\;893.16}\\ { - 1.93{\rm{M}}} \end{array}} \right]\mathit{\boldsymbol{y}},}\\ {\left[ {\begin{array}{*{20}{c}} v\\ a \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{w_1}}\\ {{w_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {728.6}\\ {268{\rm{k}}} \end{array}} \right]\mathit{\boldsymbol{y}}。} \end{array}} \right. $ | (21) |
根据式(20)画出状态观测器框图见图 7。
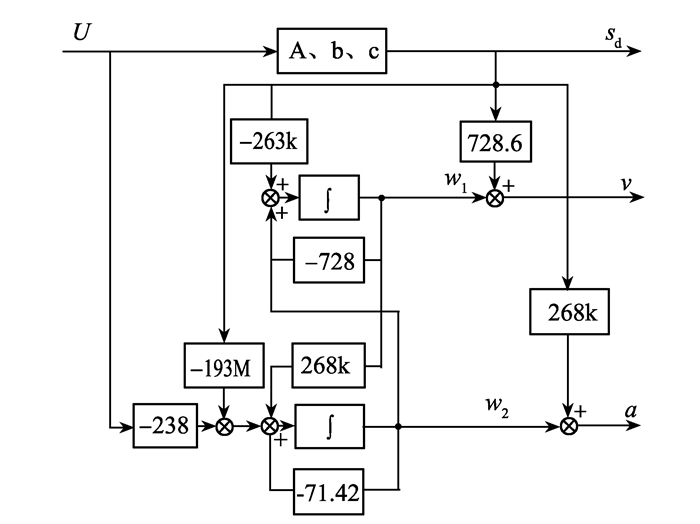
|
图 7 状态观测器框图 Figure 7 The block diagram of two-dimensional state observer |
图 7中的A、b、c为被控磁极的传递环节。PID控制器输出的电压u经过被控磁极得到悬浮间隙信号sd。从图 7中可以看出,状态观测器的输入为控制器输出电压u,V。
4 起浮过程的观测器仿真试验与结论在Simulink中对原有的控制系统添加状态观测器,状态观测器添加在被控对象两端,被控磁极的输入u与输出sd均为观测器的输入信号。原有的PID控制系统保持不变见图 8。

|
图 8 加入状态观测器后系统的框图 Figure 8 The block diagram of the system after adding the two-dimensional state observer |
选取实际磁悬浮平台的参数作为仿真参数:RL=6 Ω,u0=4π×107,A=366 mm2,磁悬浮平台质量3 kg,悬挂铁块4 kg,N=340,S0=0.6 mm,I0=1 A。得到仿真结果见图 9~11。

|
图 9 起浮过程悬浮间隙随时间变化 Figure 9 The Change of suspension clearance with time infloating process |
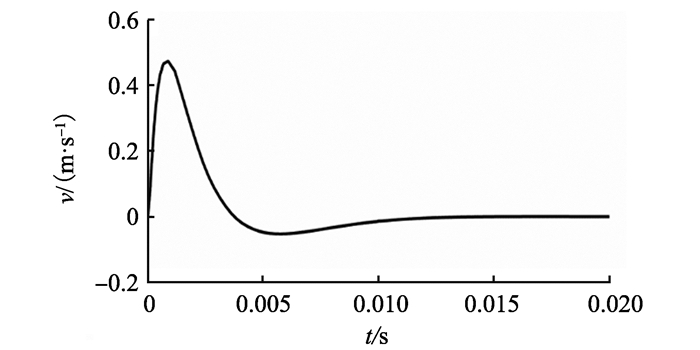
|
图 10 起浮过程垂直方向速度随时间变化估计值 Figure 10 The vertical velocity changes with time infloating process |
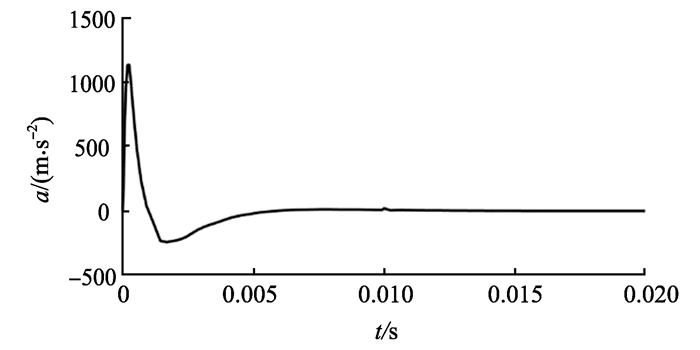
|
图 11 起浮过程垂直方向加速度随时间变化估计值 Figure 11 The vertical acceleration changes with timein floating process |
图 9给出了加状态观测器后系统起浮的间隙随时间变化的情况。此时,系统仍然能在起浮后的0.02 s内进入稳定状态,说明添加状态观测器后的系统鲁棒性良好,观测器的闭环极点选取合理。添加的观测器并不会对原本系统的稳定性产生影响。
图 10反映磁悬浮平台速度的估计值。速度是一个先升后降的变化趋势,大约在0.014 s的时候速度降为0 m/s。这段时间内悬浮的间隙应该保持增加,这一点也正与图 9中悬浮间隙的变化规律一致。平台垂直方向上的速度在0.016 s的时候稳定为0 m/s,此时平台进入稳定状态悬浮间隙不再变化。正如图 9中所示平台到达稳定悬浮间隙0.6 mm。仿真说明观测器能准确地估计磁悬浮平台垂直方向上速度的信息。
图 11是对磁悬浮平台的加速度进行的估计,加速度反映受力的情况。可以看到磁悬浮平台在0.001 6 s内受到垂直向上的合力最大。这说明开通电源之后,线圈经过短暂的充电,其电流达到最大值。这与磁悬浮平台的起浮规律也是相吻合的。由于,控制系统的位移刚度kss>0, 所以当悬浮间隙小于额定值时平台受到向上的合力,大于额定值时平台受到向下的合力。将图 9和图 11对比来看,加速度的估计值也满足上述规律。
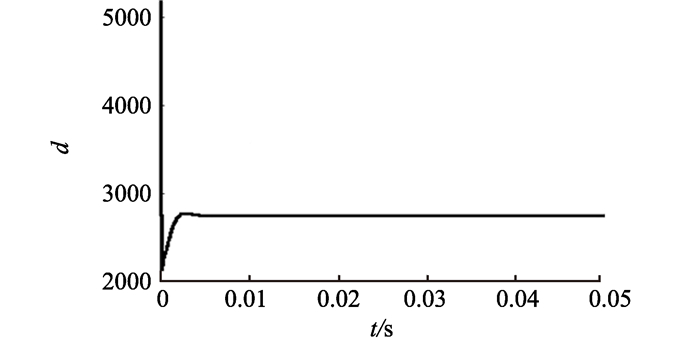
4.2 磁悬浮平台阻尼特性 4.2.1 阻尼估算结果将观测器的仿真获得的数据代入到式(2)中可以得到起浮过程阻尼随时间变化的估计值见图 12。
|
图 12 起浮过程阻尼随时间变化估计值 Figure 12 The damping changes with time in floating process |
图 12反映磁悬浮平台阻尼系数的估计值。图中0时刻阻尼的估计值为无穷大,这是由于分母中的
根据文献[11]可知,磁悬浮PID控制系统系统的阻尼决定式为
| $ d = {k_{{\rm{si}}}}{A_{\rm{a}}}{A_{\rm{s}}}{k_{\rm{d}}} - \frac{{{A_{\rm{a}}}{A_{\rm{s}}}{k_{\rm{i}}}}}{{{\omega ^2}}}, $ | (22) |
式中ω为外界干扰的频率,Hz。没有其他外界干扰时,系统理论上的阻尼系数d=ksiAaAskd应该为定值2 700。图 12中的短暂上升阶段是由系统中的延时环节造成的。图 12中仿真估算所得阻尼系数与理论上的结果基本一致。
4.2.2 减少系统负阻尼出现的讨论式(22)中,系统运行中无外界干扰时
本研究基于磁悬浮平台控制系统构筑了估计磁悬浮平台垂直方向上速度和加速度信息的状态观测器。为了保持原系统的鲁棒性不变的情况下对加入观测器的系统进行了极点配置。仿真试验结果表明, 该观测器能准确地估计磁悬浮平台垂直方向上速度和加速度信息。通过该观测器的应用实时获取阻尼信息,记录试验过程中出现负阻尼的情况,观测试验中悬浮振荡时阻尼系数的变化规律。
本研究中对磁悬浮平台获取磁极垂直方向上的速度与加速度的实时信息,在研究磁悬浮悬浮列车磁极的阻尼系数、吸死趋势判定等方面也是适应的,该研究为了解系统运行状态提供了可行性。
| [1] | 刘豹, 唐万生. 现代控制理论[M]. 天津: 机械工业出版社, 2006. |
| [2] |
汪华峰. 基于滑模状态观测器的正弦波PMSM控制策略研究[D]. 成都: 西南交通大学, 2007.
WANG Huafeng. Research on sinusoidal PMSM control strategy based on sliding mode state observer[D]. Chendu: Southwest Jiaotong University, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1131187 |
| [3] |
赵士鑫. 基于状态观测器的倒立摆控制系统的设计与研究[D]. 沈阳: 东北大学, 2009.
ZHAO Shixin. The design and study of the inverted pendulum control system based on state observer[D]. Shenyang: Northeastern University, 2009. |
| [4] |
周军, 水尊师, 葛致磊. 基于鲁棒状态观测器的运载火箭姿态控制系统设计[J].
航天控制, 2012, 30(2): 11-16 ZHOU Jun, SHUI Zunshi, GE Zhilei. Design of attitude control system for launch vehicle based on robust state observer[J]. Aerospace Control, 2012, 30(2): 11-16 |
| [5] |
范友鹏, 刘淑琴, 李红伟, 等. 基于干扰观测器的磁轴承开关功放延时补偿[J].
电机与控制学报, 2013, 17(5): 103-109 FAN Youpeng, LIU Shuqin, LI Hongwei, et al. Time-delay compensation of magnetic bearing switching power amplifier based on disturbance observer[J]. Electric Machines and Control, 2013, 17(5): 103-109 |
| [6] | 胡业发. 磁力轴承的基础理论与应用[M]. 天津: 机械工业出版社, 2006. |
| [7] | 朱宁. 自动控制理论[M]. 北京: 清华大学出版社, 2014. |
| [8] |
陈安安. 磁悬浮平台控制系统的研究[D]. 济南: 山东大学, 2016.
CHEN An'an. Research on the control system of magnetic levitation platform[D]. Jinan: Shandong University, 2016. |
| [9] |
张颖, 陈慧星, 李云钢. 电磁永磁混合EMS型磁浮列车的吸死防护问题研究[J].
兵工自动化, 2009, 28(1): 59-61 ZHANG Yin, CHEN Huixing, LI Yungang. Study on protection against suspension contact in hybrid EMS Maglev Train[J]. Ordnance Industry Automation, 2009, 28(1): 59-61 |
| [10] |
马印才, 王春平, 贾占强. 二阶PID电路状态观测器MATLAB实现[J].
科学技术与工程, 2007, 7(19): 5088-5090 MA Yincai, WANG Chunpin, JIA Zhanqiang. Implementation of state observer for second order PID circuits by MATLAB[J]. Science Technology and Engineering, 2007, 7(19): 5088-5090 DOI:10.3969/j.issn.1671-1815.2007.19.070 |
| [11] |
卢长明. 主动磁悬浮转子刚度、阻尼分析与研究[D]. 武汉: 武汉理工大学, 2008.
LU Changming. Analysis and research on stiffness and damping of active magnetic levitation rotor[D]. Wuhan: Wuhan University of Technology, 2008. |
| [12] | SHIBATA T. Precise asymptotics of boundary layers for damped simple pendulum equations[J]. Results in Mathematics, 2010, 58(1-2): 105-118 DOI:10.1007/s00025-009-0009-5 |
| [13] | SHIBATA T. Layer structures for the solutions to the perturbed simple pendulum problems[J]. Journal of Mathematical Analysis & Applications, 2006, 315(2): 725-739 |
| [14] | LIU W Y, CHEN Z H, GE X. Chaotic motion in bounded noise perturbation of simple pendulum and harmonic oscillator: international journal of nonlinear sciences and numerical simulation[J]. International Journal of Nonlinear Sciences & Numerical Simulation, 2003, 4(2): 161-168 |
| [15] | GUO Q, LIU G, XIANG B, et al. Robust control of magnetically suspended gimbals in inertial stabilized platform with wide load range[J]. Mechatronics, 2016, 39: 127-135 DOI:10.1016/j.mechatronics.2016.08.003 |
| [16] | SUN Q L, SUN Z Y. A simple control strategy to stabilize an inverted pendulum system[J]. Advanced Materials Research, 2012, 433-440: 3997-4002 DOI:10.4028/www.scientific.net/AMR.433-440 |
| [17] | DEHROUYEH A M, DEHROUYEH M, TORABI M, et al. An investigation into size-dependent vibration damping characteristics of functionally graded viscoelastically damped sandwich microbeams[J]. International Journal of Engineering Science, 2015, 96: 68-85 DOI:10.1016/j.ijengsci.2015.07.008 |
| [18] | CHA J, JANG E J, MIN J, et al. On the exact solutions of the damped harmonic oscillator with a time-dependent damping constant and a time-dependent angular frequency[J]. Journal of the Korean Physical Society, 2015, 67(2): 404-408 DOI:10.3938/jkps.67.404 |
| [19] | ERAZO K, HERNANDEZ E M. A model-based observer for state and stress estimation in structural and mechanical systems: Experimental validation[J]. Mechanical Systems & Signal Processing, 2014, 43(1-2): 141-152 |
| [20] | PAIMUSHIN V N, FIRSOV V A, GYUNAL I, et al. Theoretical-experimental method for determining the parameters of damping based on the study of damped flexural vibrations of test specimens. 1.experımental basıs[J]. Mechanics of Composite Materials, 2014, 50(2): 127-136 DOI:10.1007/s11029-014-9400-8 |
| [21] | KREBS S, SCHNURR C, PFEIFER M, et al. Reduced-order hybrid interval observer for verified state estimation of an induction machine[J]. Control Engineering Practice, 2016, 57: 157-168 DOI:10.1016/j.conengprac.2016.09.004 |
| [22] | WANG G S, LIANG B, TANG Z X. A parameterized design of reduced-order state observer in linear control systems[J]. Procedia Engineering, 2011, 15: 974-978 DOI:10.1016/j.proeng.2011.08.180 |
| [23] | WANG Q, RAN M, DONG C. Robust partial integrated guidance and control for missiles via extended state observer[J]. Isa Trans, 2016: 65 |
| [24] | ANTHONY D K, SIMÓN F. Improving the accuracy of the n -dB method for determining damping of non-lightly damped systems[J]. Applied Acoustics, 2010, 71(4): 299-305 DOI:10.1016/j.apacoust.2009.11.003 |




