电磁轴承作为一种新型轴承,利用可控电磁力将转子悬浮于给定位置,具有无机械接触、无机械摩擦、无需润滑和轴承支承特性可调等优点,广泛应用于各种高速、超洁净和减振降噪等特殊场合中[1-3]。在工程实践中,为了获得较高的功率密度,电磁轴承系统要求在满足承载力的同时尽量减小体积,因此需要对电磁轴承进行结构优化设计。本研究主要针对传统结构的轴向电磁轴承,在转子推力盘直径和转子芯轴直径不变的条件下,分析定子线槽结构参数对轴承磁场分布和承载力的影响;然后在优化的定子线槽结构参数下,研究轴承定子内孔与转子间的径向漏磁气隙对轴承磁场分布和承载力的影响,为轴向电磁轴承的结构优化设计提供一种参考。
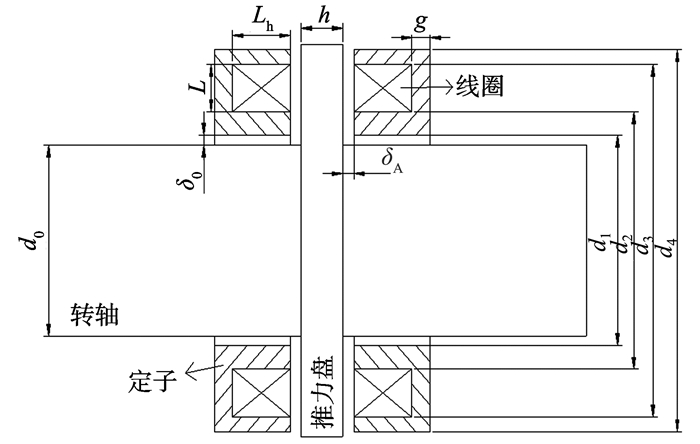
1 轴向电磁轴承基本参数和结构 1.1 轴向电磁轴承的传统结构轴向电磁轴承的传统结构如图 1所示,在转子推力盘两侧各布置一个轴向电磁轴承定子,通过控制左右两侧的轴承定子施加于转子推力盘上的轴向电磁力,控制转子的轴向位移,使转子推力盘悬浮于给定位置。根据应用场合的不同,两侧的轴向电磁轴承定子可以采用不同的结构形式。
|
图 1 轴向电磁轴承典型结构示意图 Figure 1 The typical structure of axial magnetic bearing d0—转子芯轴直径;d1—定子内径;d2—线槽内径;d3—线槽外径;d4—定子外径;δA—轴向气隙;δ0—轴承定转子间径向气隙;h—推力盘厚度;L—线槽径向长度;Lh—线槽轴向长度;g—磁轭厚度 |
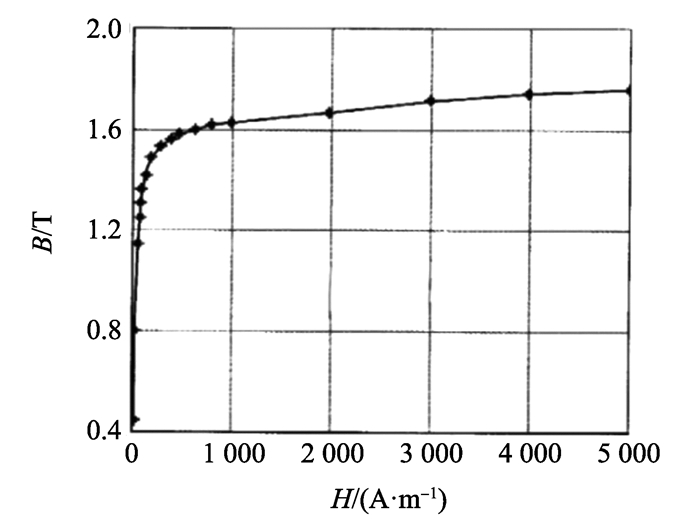
为减小电磁轴承工作时的非线性特性并防止其磁饱和,一般选取铁磁材料磁化曲线的线性部分作为电磁轴承的工作范围[4-5]。适用于电磁轴承的铁磁材料有很多种,本研究选取的是电工纯铁,其磁感应强度随磁场强度H变化曲线如图 2所示,磁化曲线线性区间的磁感应强度为0~1.4 T,本研究取最大磁感应强度Bmax=1.2 T。
|
图 2 电工纯铁磁化曲线 Figure 2 B-H curve of pure iron |
轴向气隙依据转子芯轴直径和应用场合要求而定。一般在d0 < 100 mm时,δA=0.3~0.6 mm[6],δ0=(3~10)δA。
根据安培环路定理,忽略铁芯磁阻,则线圈匝数[7]
| $ N = \frac{{2{B_{\max }}{\delta _{\rm{A}}}}}{{{\mu _0}{I_{\max }}}}, $ |
式中:Imax为线圈中的最大电流;μ0为真空磁导率。
| $ {F_{\rm{t}}} = \frac{{B_{\max }^2S}}{{{\mu _0}}}, $ |
式中S为磁极面积。
如图 1所示,线槽的横截面积为Aw=L×Lh,且
| $ {A_{\rm{w}}} = \frac{{N\pi d_{\rm{w}}^2}}{{4\eta }}, $ |
式中:η为占空比,取为0.6;dw为线圈导线直径,
在不考虑漏磁的情况下,为了使内、外环磁极轴向气隙处的磁感应强度相等,定子内、外环磁极面积应相等[13-14],根据这一原则可得出:
| $ \begin{array}{l} {d_1} = {d_0} + 2{\delta _0}, \\ {d_3} = {d_2} + 2L, \\ S = \pi \left( {d_4^2-d_3^2} \right)/4 = \pi \left( {d_2^2-d_1^2} \right)/4。\end{array} $ |
为保证定子铁心内部磁场不饱和,还需满足:
| $ S = \pi {d_2}g。$ |
本研究给定推力盘外径为82 mm,d0=40 mm,δA=0.3 mm,Imax=4 A,dw=1 mm,计算得到的线圈匝数为144匝,δ0=2 mm,d1=44 mm,h=10 mm。为了研究线槽形状对轴向电磁轴承磁场和承载力的影响,保持线槽横截面积不变,设计了线槽长宽比Ks=Lh/L不同的轴向电磁轴承,其结构参数如表 1所示。
| 表 1 轴向电磁轴承参数表 Table 1 Parameters of axial magnetic bearing |
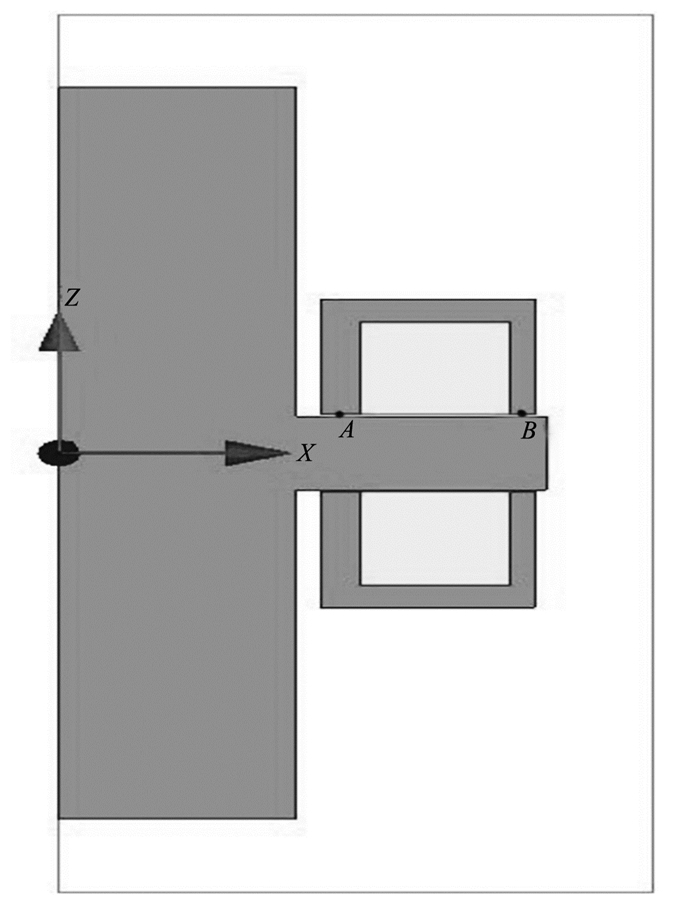
轴向电磁轴承是轴对称结构,因此,对其进行电磁场仿真时,可以采用圆柱坐标系,建立的二维静态磁场的仿真模型如图 3所示。其中A、B两点分别位于内、外环磁极气隙的中点。该模型中转子芯轴、推力盘及定子铁心均采用电工纯铁,线圈材料为铜,其余部分为空气。
|
图 3 轴向电磁轴承仿真模型 Figure 3 Simulated model of axial magnetic bearing |
边界条件设置为磁力线平行于边界,即边界处A=0;电流激励设置为576 A·匝;将模型按最大边长为0.3 mm的三角形单元格进行网格划分[15-18]。
2.2 仿真结果在保持δ0=2 mm不变时,仿真得到的轴承磁力线分布如图 4所示(图中A为磁通密度),最大轴向电磁力FS、内外环磁极气隙处磁感应强度Bi和Bo及主要气隙界面上的磁通等如表 2所示。其中,Bi和Bo分别为图 3中A、B两点处的仿真磁感应强度,Φ1s为定子内孔壁面处的漏磁通,Φis和Φos分别为定子内、外磁环处的仿真磁通,定义仿真漏磁比Δs=Φ1s/Φos。

|
图 4 仿真轴向电磁轴承磁力线分布图 Figure 4 The simulated magnetic field distribution |
| 表 2 电磁力、磁感应强度及磁通仿真结果 Table 2 The simulated electromagnetic force, magnetic induction and magnetic flux |
磁阻计算公式
| $ {R_{\rm{m}}} = l/\left( {\mu {S_1}} \right), $ |
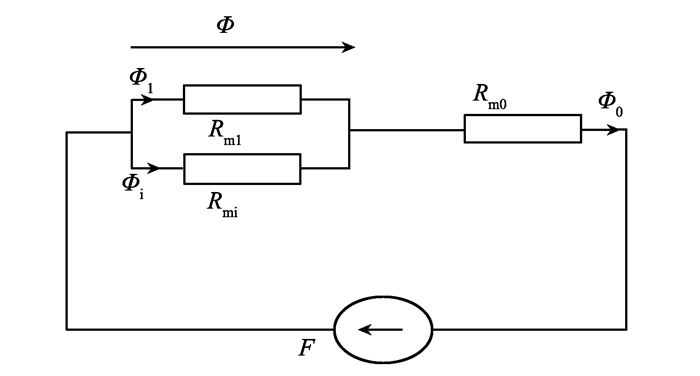
式中μ为磁导率。可知,磁阻与长度l成正比,与横截面面积S1成反比。在不考虑线槽内的漏磁及铁芯的磁阻时,磁路中的气隙磁阻主要包括内环磁极处的气隙磁阻(简称内环磁阻)Rmi、外环磁极处的气隙磁阻(简称外环磁阻)Rmo和内环磁极的内侧壁即定子内孔壁面与转轴间的径向气隙处的气隙磁阻(简称漏磁磁阻)Rm1。根据磁路关系可知,Rmi与Rm1并联后再与Rmo串联,如图 5所示。可知Φ1与Φi之和等于Φo,并且内磁环处的Φi与Bi均小于外磁环处。在考虑Rm1后,磁路的总磁阻减小,总磁通增加,导致Bo大于设计值1.2 T。由表 2可知,该模型中Bi,Bo均小于1.4 T,模型中磁通没有饱和。
|
图 5 磁路图 Figure 5 Magnetic circult of axial magnetic bearing |
根据气隙磁阻计算公式,可得
| $ \left\{ \begin{array}{l} {R_{{\rm{mi}}}} = R = \frac{{{\delta _{\rm{A}}}}}{{{\mu _0}S}}\\ {R_{{\rm{mo}}}} = R = \frac{{{\delta _{\rm{A}}}}}{{{\mu _0}S}}\\ {R_{{\rm{ml}}}} = \frac{1}{{2\pi {\mu _0}\left( {{L_{\rm{h}}} + g} \right)}}\ln \frac{{{d_1}}}{{{d_0}}} \end{array} \right., $ | (1) |
根据图 5的磁路图,可得各部分磁通
| $ \left\{ \begin{array}{l} {\mathit{\Phi} _{\rm{o}}} = \frac{{{R_{{\rm{ml}}}} + R}}{{2{R_{{\rm{ml}}}}R + {R^2}}}F\\ {\mathit{\Phi} _{\rm{i}}} = \frac{{{R_{{\rm{ml}}}}}}{{2{R_{{\rm{ml}}}}R + {R^2}}}F\\ {\mathit{\Phi} _{\rm{l}}} = \frac{R}{{2{R_{{\rm{ml}}}}R + {R^2}}}F \end{array} \right., $ | (2) |
则理论计算漏磁比
| $ {\Delta _{{\rm{t1}}}} = \frac{{{\mathit{\Phi} _1}}}{{{\mathit{\Phi} _0}}} = \frac{R}{{{R_{{\rm{ml}}}} + R}}, $ | (3) |
此时,轴向电磁轴承的电磁力
| $ {F_{{\rm{t1}}}} = \frac{{\mathit{\Phi} _{\rm{i}}^2 + \mathit{\Phi} _{\rm{o}}^2}}{{2{\mu _0}S}}。$ | (4) |
根据式(2)及仿真结果,给出了内环磁通、外环磁通及漏磁通随线槽径向长度L的变化趋势,如图 6所示。由图 6可知,当L < 5 mm,理论磁通均大于仿真值,且Φi及Φo的变化趋势与Φis,Φos相反,误差较大,主要原因是理论计算中忽略了定子线槽内的气隙磁阻和铁芯磁阻,此时线槽漏磁严重,图 5所示的磁路模型不能很好的模拟实际情况。当L>5 mm后,线槽内磁阻较大,漏磁较小,对磁通量的影响较小,仿真磁通和理论值的变化趋势相同;由于边缘效应,Φo大于Φos。
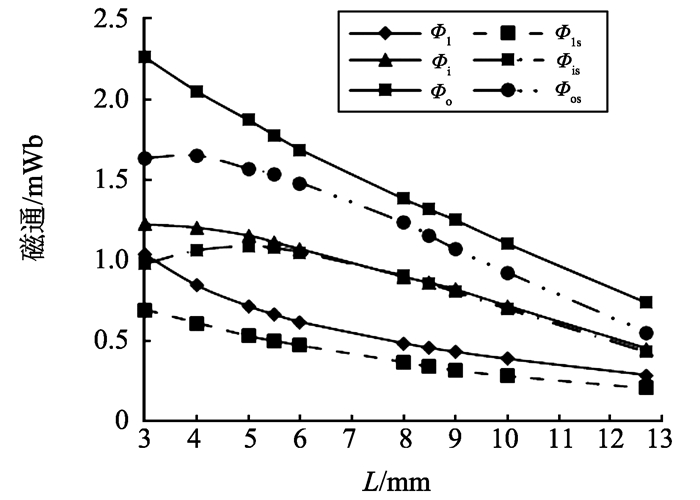
|
图 6 磁通与L的关系曲线 Figure 6 The relationship between magnetic flux and L |
根据式(3)及仿真结果,得出了漏磁比Δt1和Δs随L的变化关系,如图 7所示。由图 7可知,Δs与Δt1的变化趋势相同,都是先减小后增大,约L=8.5 mm时,即Ks=2.22时取得最小值29.6%,且Δs小于Δt1。根据仿真结果可知,漏磁比最小时,承载力并不是最大。
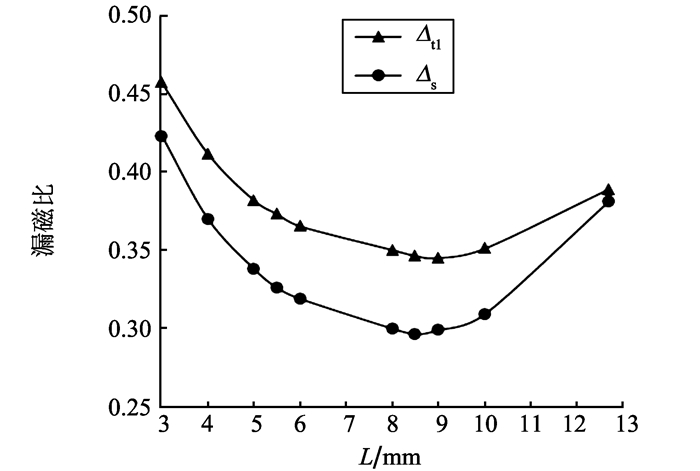
|
图 7 电磁轴承气隙漏磁比与线槽径向长度关系曲线 Figure 7 The relationship between airgap ratio and L ofaxial magnetic bearing |
根据表 1、2及式(4),分别绘出Ft、Ft1及Fs随L的变化趋势,如图 8所示。由图 8可知:Ft和Ft1均随L的增加而线性减小。当L < 5 mm时,定子线槽存在较大漏磁,Fs随L的增加先增加后减小,在L=5.5 mm即Ks=5.36处Fs取得最大值,且为理论值的88.7%;当L>5.5 mm后,Fs随L的增加而减小,与Ft的变化趋势大致相同。Ks=5~10时,电磁力基本不受线槽尺寸的影响,均保持较大值。
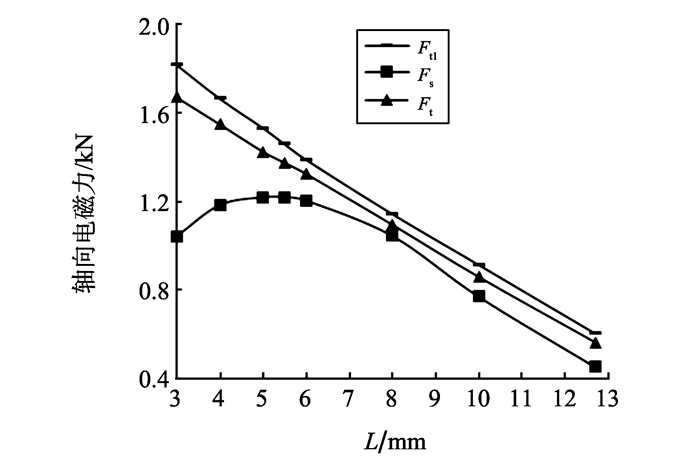
|
图 8 轴向电磁力与线圈边长关系曲线 Figure 8 The relationship between axial electromagnetic force and L |
为研究δ0对承载力的影响,在L=5.5 mm即轴向电磁力最大时,通过改变转子芯轴直径改变δ0,设气隙比Kc=δ0/δA,对轴承的磁场分布和轴向电磁力进行仿真分析。
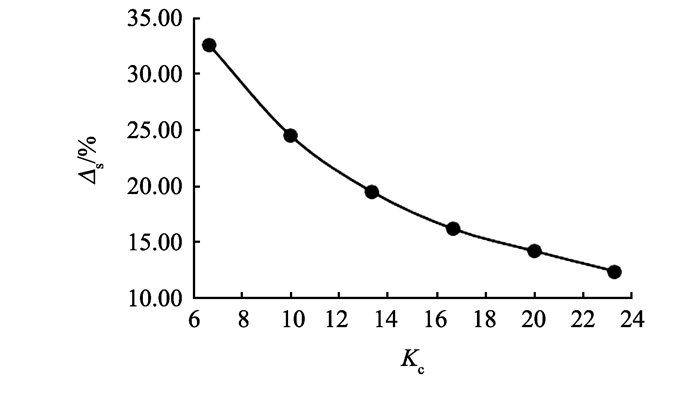
仿真得到的轴承磁力线分布如图 9所示,Δs随Kc的变化如图 10所示。可见,随Kc的增加,定转子间的漏磁明显减少,当Kc>13后,Δs减小速度变缓,由原来的32.6%降至20%左右。
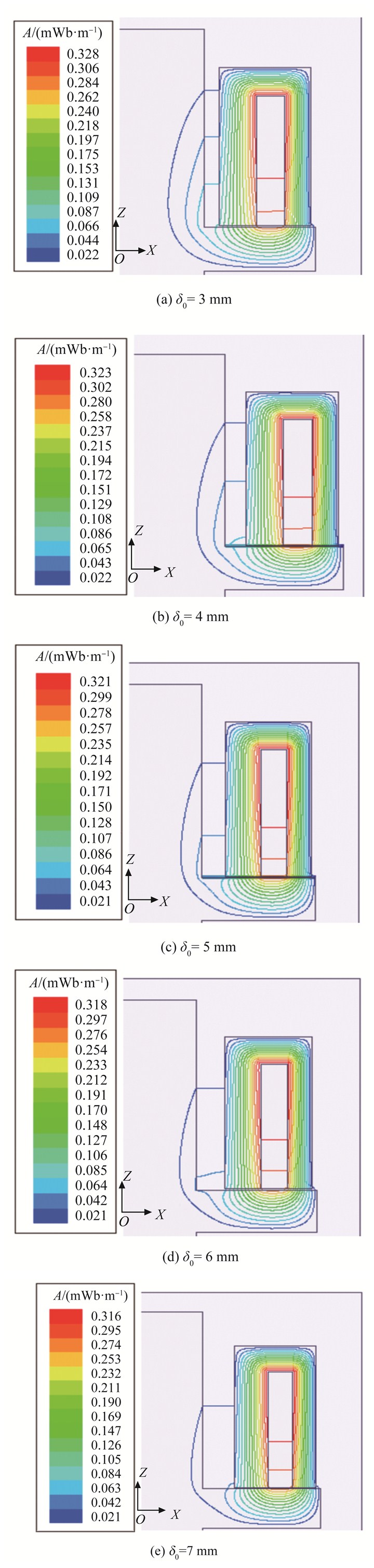
|
图 9 不同径向气隙时轴向轴承的磁力线分布 Figure 9 The magnetic flux distribution of axial magnetic bearing with different radial airgap δ0 |
|
图 10 仿真漏磁比随气隙比变化关系 Figure 10 The relationship between the Δs and Kc |
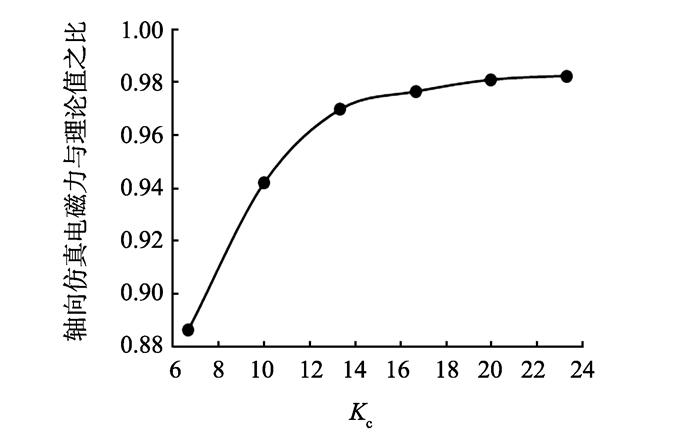
轴向电磁力Fs与Ft之比随Kc的变化关系如图 11所示,Ft为1 375 N。随着Kc的增加,Fs也随之增加,但增量越来越小,当Kc>13.3后,Kc再增加对电磁力的改善已不显著。当Kc由6.67变为13.3时,Fs与Ft的比值由88.7%增加到97.0%,轴向电磁力提升比较显著。
|
图 11 轴向电磁力仿真值与理论值之比随气隙比的变化关系 Figure 11 The relationship between the ratio of the simulatedvalue to the theoretical value and the airgap ratio |
支承高速转子的轴向电磁轴承在满足承载力的同时要求尽量减小推力盘直径,因此,本研究在推力盘直径为82 mm的条件下,设计了不同尺寸的转轴为铁磁材料的传统轴向电磁轴承,分析了线槽结构参数及定转子间的径向气隙对轴承磁场分布和承载力的影响,得出了以下结论:
(1) 定子内孔与转轴之间存在一定的径向漏磁,漏磁比随L的增大先减小后增加,当L=8.5 mm即Ks=2.22时,漏磁比取得最小值29.6%,但此时承载力并不是最大。
(2) 随L的增加,轴向电磁力先增加再减小,当L=5.5 mm即Ks=5.36时,轴向电磁力取得最大值,为不考虑漏磁时的理论电磁力的88.7%。
(3) 由于径向漏磁的存在,导致定子内环磁极的磁感应强度小于外环磁极,且二者均随L的增加先增大后减小。
(4) 定子内孔与转轴之间的径向漏磁随径向气隙的增加而减少,承载力也随之增加,当Kc达到13.3时,轴向电磁力达到不考虑漏磁时的97.0%,当气隙比继续增大时,承载力的增加非常有限。
| [1] |
闫颖鑫, 董宏林, 段广仁. 轴向磁悬浮轴承的结构设计[J].
轴承, 2006(7): 8-10 YAN Yingxin, DONG Honglin, DUAN Guangren. Structure design of axial magnetis suspension bearing[J]. Bearing, 2006(7): 8-10 |
| [2] |
袁崇军, 曹杰, 杨涌. 电磁轴承的结构优化设计[J].
机械科学与技术, 1995(5): 29-36 YUAN Chongjun, CAO Jie, YANG Yong. The optimum design of electromagnetic bearing structure[J]. Mechanical Science and Technology for Aerospace Engineering, 1995(5): 29-36 |
| [3] |
田杰, 刘建明, 王勇. 轴向电磁轴承定子线槽形状对电磁力影响的研究[J].
机械研究与应用, 2007, 20(5): 42-43 TIAN Jie, LIU Jianming, WANG Yong. Study on the effect that the shape of axial electromagnetism bearing stator trunking on the electromagnetism force[J]. Mechanical Research & Application, 2007, 20(5): 42-43 |
| [4] |
江大川, 刘淑琴, 虞烈, 等. 电磁推力支承系统结构参数设计的研究[J].
西安交通大学学报, 1997, 31(12): 100-105 JIANG Dachuan, LIU Shuqin, YU Lie, et al. Study for designing the constructional parameters of electromagnetic thrust supporting systems[J]. Journal of Xi'an Jiaotong University, 1997, 31(12): 100-105 |
| [5] |
王澄泓, 汪希平, 周朝暾, 等. 电磁推力轴承磁场的有限元计算及漏磁分析[J].
机械设计与研究, 2004, 20(5): 52-55 WANG Chenghong, WANG Xiping, ZHOU Zhaotun, et al. FEM caculation of magnetic field and analysis on flux leakage for magnetic thrust bearing[J]. Machine Design and Research, 2004, 20(5): 52-55 |
| [6] | 胡业发, 周祖德, 江征风. 磁力轴承的基础理论与应用[M]. 北京: 机械工业出版社, 2006. |
| [7] |
蔡敏, 朱熀秋. 轴向磁轴承参数设计与性能分析[J].
微电机, 2010, 43(10): 22-25 CAI Min, ZHU Huangqiu. Parameter design and performance analysis for axial magnetic bearing[J]. Micromotors, 2010, 43(10): 22-25 DOI:10.3969/j.issn.1001-6848.2010.10.007 |
| [8] | GERHARD Schweitzer, MASLEN Eric H. Magnetic bearings: theory, design, and application to rotating machinery[M]. Beijing: Mechanical Industry Press, 2012. |
| [9] | GERHARD Schweitzer, BLEULER Hannes, ALFONS Traxler. Active magnetic bearing foundation, performance and application[M]. Beijing: New Times Press, 1997. |
| [10] |
杨芳芳, 吕建超. 推力磁轴承的优化设计与有限元分析[J].
燃气涡轮试验与研究, 2010, 23(2): 43-45 YANG Fangfang, LYU Jianchao. Optimization design and finite element analysis for thrust magnetic bearings[J]. Gas Turbine Experiment and Research, 2010, 23(2): 43-45 |
| [11] |
汪希平, 张直明, 于良. 轴向磁悬浮轴承的力学特性分析[J].
应用力学学报, 2000, 17(3): 29-34 WANG Xiping, ZHANG Zhiming, YU Liang. Analysis on dynamic performances of magnetic levitated thrust Bearing[J]. Chinese Journal of Applied Mechanics, 2000, 17(3): 29-34 |
| [12] | CHIBA A, FUKAO T, ICHIKAWA O, et al. Magnetic bearings and bearingless drives[M]. Tokyo: Newnes, 2005: 65-84. |
| [13] |
龙志强, 罗昆, 王水泉, 等. 轴向磁轴承电磁参数的计算[J].
磁性材料及器件, 2000, 31(5): 10-13 LONG Zhiqiang, LUO Kun, WANG Shuiquan, et al. The calculation of electromagnetic parameters of axial magnetic bearing[J]. Journal of Magnetic Materials and Devices, 2000, 31(5): 10-13 |
| [14] |
文湘隆, 胡业发, 陈龙. 一种轴向磁力轴承定子结构参数的确定方法[J].
轴承, 2005(7): 1-3 WEN Xianglong, HU Yefa, CHEN Long. A method to calculate structural parameters for stator of axial active magnetic bearings[J]. Bearing, 2005(7): 1-3 |
| [15] | 赵博, 张洪亮. Ansoft12在工程电磁场中的应用[M]. 北京: 中国水利水电出版社, 2013. |
| [16] |
赵韩, 李露, 王勇, 等. 电磁推力轴承结构分析[J].
机床与液压, 2006(5): 68-70 ZHAO Han, LI Lu, WANG Yong, et al. Structural analysis of an electromagnetic thrust-bearing[J]. Machine Tool & Hydraulics, 2006(5): 68-70 |
| [17] | 刘国强, 赵凌志, 蒋继娅. Ansoft工程电磁场有限元分析[M]. 北京: 电子工业出版社, 2005. |
| [18] |
王世山, 王德林.大型有限元软件ANSYS在电磁领域的使用[J].高压电器, 2002, 38(2):27-31.
WANG Shishan, WANG Delin, LI Yanming. Using software ansys to analyze electromagnetic process[J]. High Voltage Apparatus, 2002, 38(2): 27-31. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_gydq200203009 |




