随着风能、太阳能等可再生能源接入电网, 以及负荷时刻波动, 发电侧与负荷侧极易出现功率不平衡[1], 负荷高峰期电源备用过大, 负荷低谷期发电机闲置, 而需求侧响应技术可从负荷侧利用负荷削减等方式实现功率平衡。智能家居因其在用户体验、能效提升、负荷管理等方面的巨大优势[2], 得到了企业与用户的积极推广与应用。结合能源互联网通信与控制技术的发展, 家庭负荷调度在电网功率平衡中具备应用的可行性[3]。
电力系统温控型负荷不仅容量大[4-5], 且短时投切或者改变其运行方式不会对用户产生明显影响, 控制简单, 响应快, 调度方式灵活, 具有作为电力系统“削峰填谷”与控制备用的巨大潜能[6]。文献[7]给空调设定不同温度点, 并结合关断进行控制; 文献[8]对空调个体进行设定温度上、下限的分离控制; 文献[9]提出了直接控制空调负荷的双层优化调度策略。以上启停空调控制会产生4~6倍于额定功率的有功和无功冲击[10], 而变频空调可在不停机情况下改变其运行功率。文献[11]对变频空调采用神经元比例-积分-微分(proportion integration differentiation, PID)控制, 但输出快速性与超调之间无法平衡; 文献[12]采用反向传播(back propagation, BP)神经网络进行控制, 但其对数据量要求大; 文献[13]提出模糊与PID相结合控制, 但智能化程度不高, 控制容量小。电热水器可视为水电阻[14], 不存在启动电流冲击问题; 文献[15]设计电热水器用户参与市场竞争交易机制, 从经济角度调节峰谷负荷; 文献[16]根据温度变化设定电热水器开关; 文献[17]在考虑电热水器控制通讯延迟基础上, 优化控制参数, 控制效果都很好。
为了增加可调容量且避免空调关断导致的系统功率冲击, 在保证用户舒适度的情况下, 本研究提出一种结合变频空调与电热水器的联合调度控制策略。在对变频空调与电热水器消耗功率特性进行分析的基础上, 得出其相应的数学聚合模型, 并考虑变频空调负荷的多样性, 以减少峰谷差为目标, 分别对变频空调与电热水器采取不同控制方式, 响应电力系统负荷调度, 最后通过算例仿真, 验证了所提控制策略有效性, 并说明负荷数量对其响应能力的影响。
1 家庭负荷控制模型 1.1 家庭负荷特性分析常用家庭电器额定功率如表 1[1]所示。从负荷功率、使用时间、断电或变功率运行对用户影响等方面考虑, 空调与电热水器最具可控潜能。在家庭负荷中, 电热水器基本全年使用; 而空调大量使用的季节, 往往伴随着家庭负荷大幅增长, 以空调和电热水器的联合调度控制进行负荷响应功率调节, 较好地符合家庭负荷的时间特性。
| 表 1 常用家电额定功率 Table 1 Rated power of household appliances |
2012年, 中国变频空调市场销量占比只有50.6%;2013年达到了53.3%;而到2014年, 中国变频空调的零售量占比已达到57.9%, 变频空调已成为目前空调市场主流产品[18]。因此, 主要考虑变频空调参与调节。
1.2.1 变频空调节能原理变频空调通过改变压缩机转速来调节冷(热)进气量, 进而连续调节负荷, 动态适应房间温度变化, 其风机、水泵类负载的特性[19]为
| $ \left\{ \begin{array}{l} {G_1}/{G_2} = {n_1}/{n_2}\\ {H_1}/{H_2} = {\left( {{n_1}/{n_2}} \right)^2}\\ {P_1}/{P_2} = {\left( {{n_1}/{n_2}} \right)^3} \end{array} \right., $ | (1) |
式中:n1、n2为电极转速;G1、G2为水流量; H1、H2为水泵扬程; P1、P2为水泵轴功率。
转速公式为
| $ n = 60f\left( {1-s} \right)/P, $ | (2) |
式中:f表示电源频率; P为极对数; s为转差率。
由式(1)、(2)可知, 轴功率与电极转速的三次方成正比, 控制电源频率即可改变电机转速, 进而改变轴功率。因此, 降低频率即能达到节能目的, 且实现对消耗功率的连续调节。但在实际运行过程中, 若水泵运行频率降的太低, 系统水流量和水泵扬程难以得到满足, 影响系统运行, 常规变频空调频率范围为10~150 Hz, 系统需满足以下条件
| $ \left\{ \begin{array}{l} {H_{\min }} \le H \le {H_{\max }}\\ {G_{\min }} \le G \le {G_{\max }} \end{array} \right., $ | (3) |
式中:Hmax、Hmin分别表示最大和最小水泵扬程; Gmax、Gmin分别表示最大和最小水流量。
1.2.2 变频空调控制模型无论是变频空调还是定频空调, 当空调开启时, 室内温度与室外温度都存在如下关系式[3]
| $ {T^{t + 1}} = T_0^{t + 1}-\eta PR-\left( {T_0^{t + 1}-\eta PR - {T^t}} \right){{\rm{e}}^{ - \frac{{\Delta t}}{{RC}}}}, $ | (4) |
式中: P为空调制冷/热功率, kW; η为空调能效比; T0t, Tt分别表示t时刻室外、室内温度, ℃; R为等效热阻, ℃/W; C为等效热容, J/℃; Δt为仿真时间。假设空调一直开启, 且室外温度保持不变, 对式(4)进行h次迭代操作, 可以得到
| $ {T^{t + h\Delta t}} = A-\left( {A-{T^t}} \right){B^h}, $ | (5) |
式中:A=T0t-ηPR;
令A-T0t=0, T0t-Tt=ηPR, 则
| $ P = \frac{{T_0^t-{T^t}}}{{\eta R}}。$ | (6) |
此时, 空调制冷(热)量刚好维持室内外温度差, 系统保持稳定, 室内温度不再变化。综合(1)、(2)和(6)式, 设定好合理温度, 即可通过变频压缩机改变转速来实现。控制框图如图 1所示。

|
图 1 变频空调控制框图 Figure 1 Control diagram of inverter air conditioner |
拟定用户舒适温度为[Tmin, Tmax], 考虑到变频空调负荷可能处在不同温度状态, 且其数量也不相同, 将在相同温度范围内的变频空调分为一组, 假设一共有n组, 处在温度T(j)状态的空调有q(j)台, T0表示室外温度。为得到最大响应容量, 当T0≥T(j)且负荷高峰期,或T0<T(j)且负荷低谷期时, 将空调温度设定为Tmax, 当T0 < T(j)且负荷高峰期,或T0≥T(j)且负荷低谷期时, 将空调温度设定为Tmin。则对于单台变频空调, 其所能调节的最大功率
| $ \Delta {p_{{\rm{ac}}}}\left( j \right) = \left\{ \begin{array}{l} \frac{{{T_{\max }}-T\left( j \right)}}{{\eta R}}, \;温度调至{T_{\max }}\\ \frac{{T\left( j \right)-{T_{\min }}}}{{\eta R}}, \;温度调至{T_{\min }} \end{array} \right., $ | (7) |
则n组聚合空调可调容量为
电热水器是经过温控器的通断实现是否加热, 若水温低于预置临界温度下限, 温控器自动接通, 电热水器开始加热, 水温抵达预置临界温度上限, 温控器断开, 热水器停止加热。普通概念的保温, 就是短时间的加热, 加热时依然用热水器额定功率[20]。电热水器只工作在开关状态, 其消耗功率可看作只有额定功率与零电耗两种情况。
电热水器具有四个特性: (1)瞬时断电特性, 可控性强; (2)断电后立即启动特性, 控制策略设计简单; (3)储能特性, 短时断电不会影响用户体验; (4)负荷容量大, 具有作为调峰负荷的巨大潜能[5]。
1.3.2 电热水器聚合模型电热水器只有“ON”与“OFF”两种运行状态, 假设有m台电热水器, 根据功率从大到小进行排序, 其中第k台热水器的功率为Phk, 开启状态为Gk(Gk=1表示开启状态, Gk=0表示关断状态)。在负荷高峰期, 关断开启电热水器, 在负荷低谷期, 开启关断电热水器, 其聚合体可调容量
| $ \Delta {P_{\rm{h}}}\left( m \right) = \left\{ \begin{array}{l} \sum\limits_{k = 1}^m {{P_{{\rm{h}}k}}{G_k}}, \;负荷高峰期\\ \sum\limits_{k = 1}^m {{P_{{\rm{h}}k}}\left( {1-{G_k}} \right), \;负荷低谷期} \end{array} \right.。$ | (8) |
对变频空调与电热水器分析, 变频空调响应负荷波动是采用预设温度来实现的, 温度在舒适温度范围内, 其调节功率具有平滑无负荷极差特点; 电热水器采用设备启停方式来运行, 其调节功率存在负荷级差, 负荷级差为单台电热水器功率。据此, 提出变频空调与电热水器联合调度控制策略, 以夏天负荷高峰期为例, 具体步骤如下:
(1) 对电热水器功率、开关状态、室内外温度、变频空调设定温度分别进行统计, 根据负荷调度曲线, 设定死区范围[Pmin, Pmax], 确定负荷增(减)目标值
| $ {P_{{\rm{target}}}} = \left\{ \begin{array}{l} {P_{{\rm{load}}}}-{P_{\max }}, {P_{{\rm{load}}}} \ge {P_{\max }}\\ {P_{\min }}-{P_{{\rm{load}}}}, {P_{\min }} \ge {P_{{\rm{load}}}} \end{array} \right.。$ | (9) |
(2) 将电热水器按照功率大小从高到低依次编号1, 2, 3, …, m, 将Ptarget与电热水器聚合体可调容量ΔPh(m)进行比较, 若存在一个ktarget≤m, 满足
| $ P_{{\rm{rest}}}^{\left( 0 \right)} = {P_{{\rm{target}}}}-\sum\limits_{k = 1}^{{k_{{\rm{target}}}}-1} {{P_{{\rm{h}}k}}{G_k}} 。$ | (10) |
若不存在ktarget, 即Ptarget≥ΔPh(m), 则m台热水器全部关停, 同样将剩余功率Prest(0)由变频空调进行调节。剩余功率
| $ P_{{\rm{rest}}}^{\left( 0 \right)} = {P_{{\rm{target}}}}-\Delta {P_{\rm{h}}}\left( m \right)。$ | (11) |
(3) 将每组变频空调按照温度从低到高依次编号1, 2, 3, …, n, 优先调节室内外温差大的空调组, 若存在一个jtarget≤n, 满足
| $ \sum\limits_{j = 1}^{{j_{{\rm{target}}}}-1} {\Delta {P_{{\rm{ac}}}}\left( j \right)q\left( j \right)} \le P_{{\rm{rest}}}^{\left( 0 \right)} < \sum\limits_{j = 1}^{{j_{{\rm{target}}}}} {\Delta {P_{{\rm{ac}}}}\left( j \right)q\left( j \right)}, $ | (12) |
则将jtarget-1组空调温度设为Tmax, 剩余功率Prest(1)由第jtarget组变频空调进行调节, 转步骤(4)。剩余功率
| $ P_{{\rm{rest}}}^{\left( 1 \right)} = P_{{\rm{rest}}}^{\left( 0 \right)}-\sum\limits_{j = 1}^{{j_{{\rm{target}}}}-1} {\Delta {P_{{\rm{ac}}}}\left( j \right)q\left( j \right)} 。$ | (13) |
单台空调的调节功率
| $ \Delta P_{{\rm{ac}}}^{{\rm{target}}}\left( {{j_{{\rm{target}}}}} \right) = P_{{\rm{rest}}}^{\left( 1 \right)}/q\left( {{j_{{\rm{target}}}}} \right)。$ | (14) |
若不存在jtarget, 即
| $ {P_{{\rm{target}}}} \ge \Delta {P_{\rm{h}}}\left( m \right) + \sum\limits_{j = 1}^n {\Delta {P_{{\rm{ac}}}}\left( j \right)q\left( j \right)}, $ | (15) |
则n组变频空调温度全都设为Tmax。
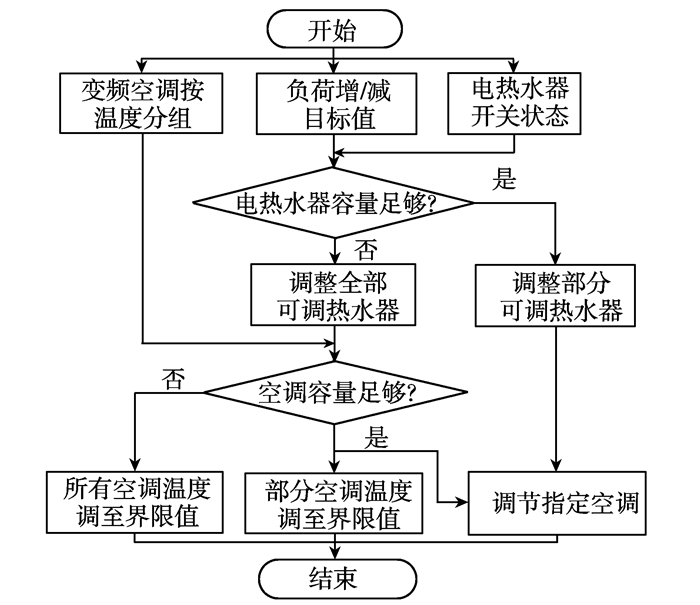
(4) 根据单台空调调节功率, 由式(6)计算其设定温度, 并由式(1)和(2)计算其压缩机运行频率, 实现对变频空调的控制。上述联合控制流程如图 2所示。
|
图 2 变频空调与电热水器联合控制流程图 Figure 2 Flow chart of combined control of variable frequency air conditioner and electric water heater |
本研究取冬季(5 ℃)某小区一天(2017年12月20日)的负荷波动曲线作为调度曲线, 每15 min一个负荷点, 共计96个点。经过统计, 有500台电热水器可被控制, 其中100台的单台功率为2 kW, 300台的单台功率为1.5 kW, 100台的单台功率为1 kW; 假设每种功率处于开关状态的电热水器数量相等, 则热水器可调节的范围为±375 kW, 同时该小区还有1 000台空调, 设定的舒适温度区域为[20.0, 26.0]℃, 将该温度区域分为13组, 温度区间为[20.0, 20.2]、[20.3, 20.7]、[20.8, 21.2]、[21.3, 21.7]、[21.8, 22.2]、[22.3, 22.7]、[22.8, 23.2]、[23.3, 23.7]、[23.8, 24.2]、[24.3, 24.7]、[24.8, 25.2]、[25.3, 25.7]、[25.8, 26.0]。第1组和第13组有空调60台, 其余各组80台, 空调平均额定功率为2.5 kW, 制热能效比2.7, 等效热容0.18 kWh/℃, 等效热阻5.56 ℃/kW[9], 则变频空调可调范围为±199.84 kW。同时为了避免频繁调节, 根据负荷波动情况, 设定功率基准为4 700 kW, 调节死区范围为[4 400, 5 000] kW。
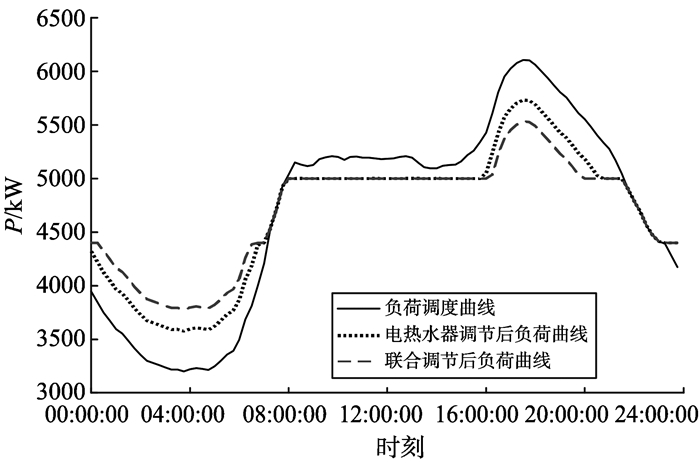
电热水器与空调的联合调控仿真结果如图 3所示。由图 3可看出, 当功率调度量在死区范围内, 即07:15—7:45和21:45—23:00时, 电热水器与空调都不参与调节, 当功率调度量超出死区范围, 电热水器和变频空调联合调控, 可以达到削峰填谷效果。
|
图 3 冬季电热水器和空调联合调控效果仿真 Figure 3 Simulation of electric water heater and air conditionercombined control in winter |
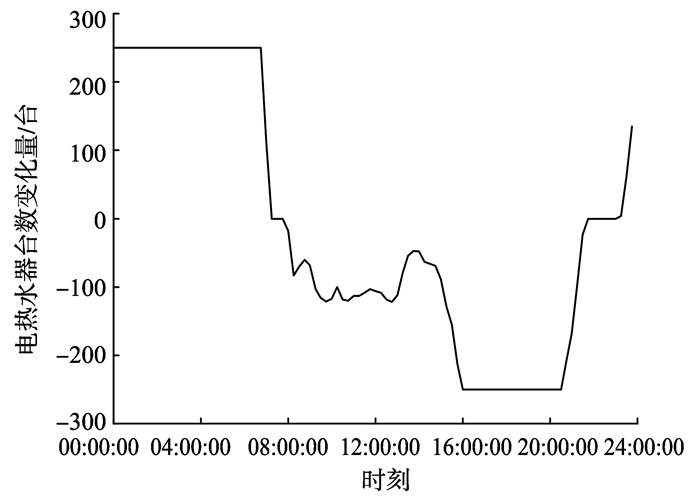
电热水器在各个时刻开关状态变化量如图 4。在图 4中, 正数表示电热水器开启台数变化量, 负数表示电热水器关停台数变化量, 可看出, 在负荷低谷期, 电热水器开启, 在负荷高峰期, 电热水器关停, 且电热水器开关台数与功率差额成正相关。
|
图 4 冬季电热水器台数变化量 Figure 4 Number change of electric water heaters in winter |
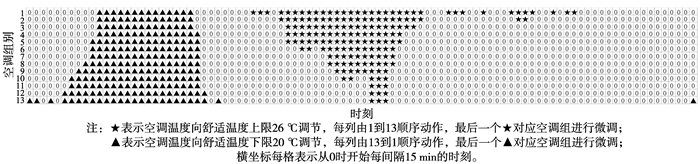
图 5是空调控制计划图, 每15 min 1个负荷点。以20:15时刻为例进行说明。

|
图 5 冬季空调控制计划图 Figure 5 Air conditioner control plan in winter |
(1) 此时负荷调度量为783 kW, 考虑调节死区需调节有功483 kW, 电热水器最大调节量为375 kW, 则变频空调需承担108 kW;
(2) 第10、11、12、13组所能调最大功率之和为103.52 kW, 第9、10、11、12、13组所能调最大功率之和为124.83 kW, 则先将10、11、12、13组温度都设为20 ℃, 此时剩余4.48 kW, 第9组每台空调需调节4.48/80=0.056 kW;
(3) 第9组开始处于24 ℃, 消耗功率为1.27 kW, (f/50)3=1.27/2.5, f=39.9 Hz; 同时(T-5)/(Rη)=(1.27-0.056), T=21.0 ℃, 将第9组空调的温度设为23.2 ℃, 频率设为39.3 Hz。
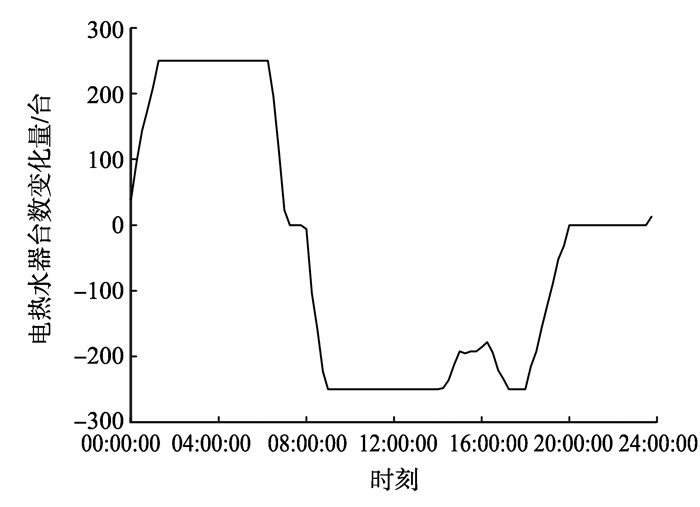
3.2 夏季情况下算例分析取夏季(30 ℃)某小区一天(2017年7月7日)的负荷波动曲线作为调度曲线, 根据负荷波动情况, 设定功率基准为3 800 kW, 调节死区范围为[3 500, 4 100]kW。变频空调和热水器相关假设条件如3.1节, 在负荷低谷期, 设定在较高温度的变频空调降低温度来消耗更多的功率, 在负荷高峰期, 设定在较低温度的变频空调升高温度来减少对功率的消耗, 调控仿真结果如图 6所示, 电热水器在各个时刻开关状态变化量如图 7所示, 变频空调控制计划图如图 8所示。

|
图 6 夏季电热水器和空调联合调控效果仿真 Figure 6 Simulation of electric water heater and air conditionercombined control in summer |
|
图 7 夏季电热水器台数变化量 Figure 7 Number change of electric water heaters in summer |
|
图 8 夏季空调控制计划图 Figure 8 Air conditioner control plan in summer |
在3.1节的基础上, 增加电热水器到1 000台, 其中200台的单台功率为2 kW, 600台的单台功率为1.5 kW, 200台的单台功率为1 kW; 假设每种功率处于开关状态的电热水器数量相等, 则热水器调节能力上下限各增大到750 kW, 空调增加为1 500台, 第1组和第13组有空调90台, 剩下各组120台, 其余设定保持不变, 则变频空调调节能力上下限各增大到299.76 kW, 进行联合调控仿真, 结果如图 9所示。
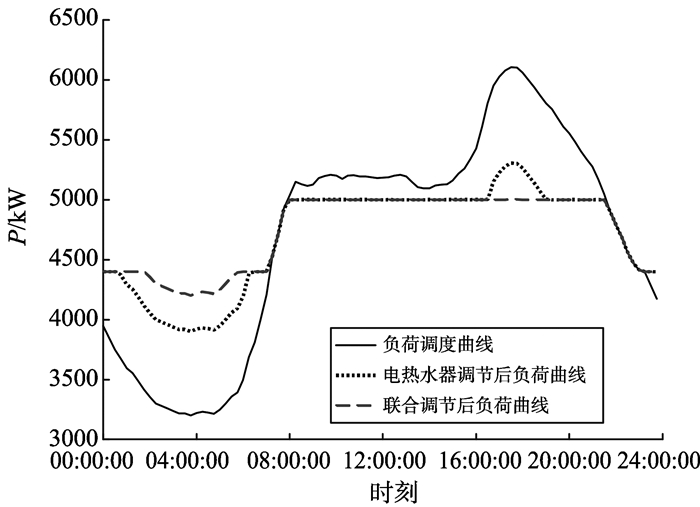
|
图 9 增加电热水器和空调数量对调度结果影响 Figure 9 Influence on the scheduling results with the increase of the number of electric water heaters and air conditioners |
由图 3与图 9对比可以看出, 增加电热水器和空调数量, 在负荷高峰时期, 功率能稳定到死区上限5 000 kW, 不存在功率大量剩余, 在负荷低谷时期, 相对于基准功率最大波动量为498 kW, 比3.1节的923 kW减小了425 kW, 且在超出调节范围的时刻也大大减少, 因此增加调节电器数量, 可以明显增加负荷调节能力, 使调节效果更加显著。
4 总结为响应负荷调度、增加可调容量、避免空调启停, 本研究提出了一种基于电热水器与变频空调的联合调度控制策略。在对电热水器与空调消耗功率特性分析基础上, 说明其可调性, 并建立相应数学模型, 同时考虑空调负荷多样性给出了具体控制决策, 为避免负荷频繁调节, 结合调度曲线设立了±300 kW范围的调节死区, 最后用MATLAB对所提出控制策略进行仿真, 验证了控制策略的有效性。所提控制策略保证了用户的舒适度, 避免了空调启停的调节方式,可响应系统功率波动, 调节范围大, 同时也说明了增加所调负荷数量可以显著提高负荷响应功率调节的能力。若功率调节量超出电热水器与变频空调的联合调控范围, 则考虑关停空调或采取转移潮流方式来响应系统调度。
| [1] |
董丹丹. 基于电热水器类温控负荷的电力系统频率稳定与控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
DONG Dandan. Research on the stabilization and control power system frequency based on EWH-A type of TCL[D]. Harbin: Harbin Institute of Technology, 2015. |
| [2] |
张新昌, 周逢权. 智能电网引领智能家居及能源消费革新[J].
电力系统保护与控制, 2014, 42(5): 59-67 ZHANG xinchang, ZHOU Fengquan. Smart grid leads the journey to innovative smart home and energy consumption patterns[J]. Power System Protection and Control, 2014, 42(5): 59-67 DOI:10.7667/j.issn.1674-3415.2014.05.010 |
| [3] | LU Ning. An evaluation of the HVAC load potential for providing load balancing service[J]. IEEE Transactions on Smart Grid, 2012, 3(3): 1263-1270 DOI:10.1109/TSG.2012.2183649 |
| [4] |
闫华光, 陈宋宋, 杜重阳, 等. 智能电网电力需求响应标准体系研究与设计[J].
电网技术, 2015, 39(10): 2685-2689 YAN Huaguang, CHEN Songsong, DU Chongyang, et al. Research and design of power demand response standard system about smart grid[J]. Power System Technology, 2015, 39(10): 2685-2689 |
| [5] |
李作锋, 杨斌, 杨永标. 基于日前调度的大规模中央空调调峰方法[J].
南方电网技术, 2017, 11(1): 74-79 LI Zuofeng, YANG Bin, YANG Yongbiao. Peak load regulation method with large scale central air-conditioning load based on day-ahead dispatch[J]. Southern Power Grid Technology, 2017, 11(1): 74-79 |
| [6] | MASUTA T, YOKOYAMA A. Supplementary load frequency control by use of a number of both electric vehicles and heat pump water heaters[J]. Smart Grid, IEEE Transactions on, 2012, 3(3): 1253-1262 DOI:10.1109/TSG.2012.2194746 |
| [7] | PERFUMO C, KOFMAN E, BRASLAVSKY J H, et al. Load management: model-based control of aggregate power for populations of thermostatically controlled loads[J]. Energy Conversion & Management, 2012, 55(3): 36-48 |
| [8] |
周磊, 李扬, 高赐威. 聚合空调负荷的温度调节方法改进及控制策略[J].
中国电机工程学报, 2014, 34(31): 5579-5589 ZHOU Lei, LI Yang, GAO Ciwei. Improvement of temperature adjusting method for aggregated air-conditioning loads and its control strategy[J]. Chinese Journal of Electrical Engineering, 2014, 34(31): 5579-5589 |
| [9] |
高赐威, 李倩玉, 李扬. 基于DLC的空调负荷双层优化调度和控制策略[J].
中国电机工程学报, 2014, 34(10): 1546-1555 GAO Ciwei, LI Qianyu, LI Yang. Bi-level optimal dispatch and control strategy for air-conditioning load based on direct load control[J]. Chinese Journal of Electrical Engineering, 2014, 34(10): 1546-1555 |
| [10] |
郑竞宏, 朱守真, 王光, 等. 空调负荷运行特性研究及建模[J].
中国电机工程学报, 2009(10): 67-73 ZHENG Jinghong, ZHU Shouzhen, WANG Guang, et al. Key characteristics and modeling of air conditioner load[J]. Chinese Journal of Electrical Engineering, 2009(10): 67-73 DOI:10.3321/j.issn:0258-8013.2009.10.012 |
| [11] |
郑宗和, 梁江, 牛宝联, 等. 变频空调系统应用神经元PID控制的仿真研究[J].
暖通空调, 2004, 34(12): 93-95 ZHENG Zonghe, LIANG Jiang, NIU Baolian, et al. Simulation study on neural PID control of variable-frequeney air conditioning systems[J]. Heating Ventilating and Air Conditioning, 2004, 34(12): 93-95 DOI:10.3969/j.issn.1002-8501.2004.12.025 |
| [12] |
贾少青, 陈平, 李爱华. 基于神经网络的变频空调控制系统[J].
计算机测量与控制, 2006, 14(8): 1033-1035 JIA Shaoqing, CHEN Ping, LI Aihua. Control method of inverter air conditioner based on neural network[J]. Computer Measurement & Control, 2006, 14(8): 1033-1035 |
| [13] |
王淑青, 杨桦, 何涛. 模糊PID复合控制在变频空调中应用研究[J].
微计算机信息, 2006, 22(6S): 42-44 WANG Shuqing, YANG Hua, HE Tao. Research on fuzzy PID control for air-condition with frequency change[J]. Microcomputer Information, 2006, 22(6S): 42-44 |
| [14] |
孙建伟, 唐升卫, 刘菲, 等. 面向需求响应控制的家用电热水器建模和控制策略评估[J].
电力系统及其自动化学报, 2016, 28(4): 51-55 SUN Jianwei, TANG Shenwei, LIU Fei, et al. Modeling method and control strategy evaluation of electric water heater for demand response program[J]. Proceedings of the CSU-EPSA, 2016, 28(4): 51-55 |
| [15] |
王映祥. 电力市场下大规模电热水器用户的需求侧竞价研究[D]. 长沙: 长沙理工大学, 2012.
WANG Yingxiang. Research on bidding strategy for large-scale electric water heater user participating power market[D]. Changsha: Changsha University of Science and Technology, 2012. |
| [16] | KONDOH J, LU N, Hammerstrom D J. An evaluation of the water heater load potential for providing regulation service[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1309-1316 DOI:10.1109/TPWRS.2010.2090909 |
| [17] | ZHANG Y, LU N. Parameter selection for a centralized thermostatically controlled appliances load controller used for intra-hour load balancing[J]. IEEE Transactions on Smart Grid, 2013, 4(4): 2100-2108 DOI:10.1109/TSG.2013.2258950 |
| [18] | 中关村在线. 2014-2015中国空调市场年度报告[EB/OL]. (2015-02-05)[2017-12-15]. http://tech.hexun.com/2015-02-05/173107490.html. |
| [19] |
胡雪梅, 任艳艳. 中央空调的变频控制设计及节能分析[J].
电机与控制应用, 2011, 38(7): 44-47 HU Xuemei, REN Yanyan. Design and energy saving analysis of frequency conversion control in central air conditioning[J]. Motor and Control Applications, 2011, 38(7): 44-47 |
| [20] | 王华丽. 电热水器的工作原理是什么[EB/OL]. (2014-11-14)[2017-12-15]. http://www.c-ps.net/jishu/zhinengfenxi/211998.html. |



