2. 山东农业大学机械与电子工程学院, 山东 泰安 271018;
3. 山东省园艺机械与装备重点实验室, 山东 泰安 271018;
4. 山东电力设备有限公司, 山东 济南 250022
2. Mechanical & Electronic Engineering College, Shandong Agricultural University, Tai′an 271018, Shandong, China;
3. Shandong Provincial Key Laboratory of Horticultural Machineries and Equipments, Tai′an 271018, Shandong, China;
4. Shandong Power Equipment Company, LTD, Jinan 250022, Shandong, China
基于图像的目标识别和分类方法很多, 从全局和局部图像特征提取研究方向上分, 目前常用的目标识别算法主要有基于局部特征提取与匹配的方法和基于全局图像特征的模板匹配的方法[1-2]。基于局部特征的物体识别方法主要利用图像中兴趣点的邻域信息来描述图像, 用局部信息构造出具有光照、几何变换不变性的描述子, 然后通过特征匹配、模式识别等完成对物体的识别。这类方法是近几年的研究热点, 但对于物体表面纹理不丰富的物体仍然存在识别效果差的问题[3-5]。本研究采用一种改进型模板匹配算法提取图像的梯度特征, 结合提取图像梯度的相似性度量法、鲁棒性很强的梯度直方图(histogram of oriented gradient, HOG)法[6-7]以及基于文献[8]中在线学习方法的优势, 借鉴文献[9]提出的主方向模板(dominant orientation templates, DOT)算法, 去除次要的梯度特征, 只采用主要幅值大的梯度方向作为模板特征进行匹配, 并通过将模板特征二进制化来提高速度, 达到实时在线识别目标[10-12]。试验证明, 本研究采用的目标识别算法在识别纹理较少的物体时效果较好, 并能在线同时识别多个不同物体、多视角识别一个三维物体, 对于微小变形、微小平移和光照变换的物体识别效果鲁棒性较强。
1 改进型模板匹配目标识别算法 1.1 相似性度量定义初始的相似性度量函数ε1, 用来计算输入图像I与中心特征点为c的模板图像之间梯度方向的相似的个数。函数定义为
| $ {\varepsilon _1}\left( {I, O, c} \right) = \sum\limits_r \delta \left( {{\rm{ori}}\left( {I, c + r} \right) = {\rm{ori}}\left( {O, r} \right)} \right), $ |
式中:δ(P)是返回值为1或0的二进制函数; ori(O, r)是模板图像O在位置r处的离散梯度方向; ori(O, c+r)是输入图像I在位置c+r处的离散梯度方向。
1.2 加入对微小变形和微小平移的不变性为了使相似性度量方法保持对微小变形的稳定性, 同时加快计算速度, 本研究将不考虑图像中的所有像素点的梯度方向, 而是将两幅图像分解为很小的规则正方形区域R, 仅考虑每个小区域R的主要的梯度幅值大的像素点的梯度方向。此时, 可将相似性度量函数修改为
| $ {\varepsilon _2}\left( {I, O, c} \right) = \sum\limits_{R\;{\rm{in}}\;O} \delta \left( {{\rm{do}}\left( {I, c + R} \right) \in {\rm{DO}}\left( {O, R} \right)} \right), $ |
式中:DO(O, R)是模板图像O中每个小区域R中的梯度幅值大的像素点梯度方向的集合; 而do(I, c+R)返回是输入图像I在区域R平移c后的梯度方向中强度最大的一个方向向量。考虑到可以准确快速获得每个小区域R的最大梯度方向, 并且它对噪声和光照变化的鲁棒性强, 所以选取模板图像O中每个区域R的最大梯度方向代表区域R。同时, 为了描述整个2×2区域, 引入符号“⊥”来表示这个区域内没有可利用的梯度信息。因此, 函数DO(·)返回值要么是区间[0, n0-1]的不同梯度的梯度方向, 要么返回{⊥}, 函数原型可以定义为
| $ {\rm{DO}}\left( {O, R} \right) = \left\{ {\begin{array}{*{20}{l}} {S\left( {O, R} \right), }&{{\rm{if}}\;S\left( {O, R} \right) \ne 0}\\ {\left\{ \bot \right\}, }&{{\rm{otherwise}}} \end{array}} \right., $ | (1) |
| $ \begin{array}{l} {\rm{with}}\;\;\;\;\;\;\;\;\;\;\;\;S\left( {O, R} \right) = \{ {\rm{ori}}\left( {O, l} \right):\\ \;\;\;\;\;\;l \in \max {\rm{ma}}{{\rm{g}}_k}\left( R \right) \wedge {\rm{mag}}\left( {O, l} \right) > \tau \}, \end{array} $ | (2) |
式中: l是区域R中的一个像素点; ori(O, l)是模板图像O在像素点l处的梯度方向; mag(O, l)是模板图像O在像素点l处的大小。max magk(R)是区域R中k个最大梯度方向的位置, 为了提高在线运行的速度, 取k=1。τ是根据梯度的大小决定该区域是否为相同区域的阈值。
为了保持相似性度量方法对微小平移的不变性, 在不增加目标识别错误率的前提下, 分析整幅图像时仅考虑有限几个位置c而不是全部图像进行扫描, 可以节省大量时间。为了达到这个目的, 在目标物体发生微小平移时, 选取函数ε2的最大返回值作为相似性度量标准, 函数ε3可表示为
| $ \begin{array}{l} {\varepsilon _3}\left( {I, O, c} \right) = \mathop {\max }\limits_{m \in M} {\varepsilon _2}\left( {I, w\left( {O, m} \right), c} \right) = \\ \;\;\;\;\;\mathop {\max }\limits_{m \in M} \sum\limits_{R\;{\rm{in}}\;O} \delta ({\rm{do}}\left( {I, c + R} \right) \in \\ \;\;\;\;\;{\rm{DO}}\left( {w\left( {O, m} \right), R} \right)), \end{array} $ |
式中w(O, m)表示模板图像O被平移了m。实际应用中, 仅考虑m为二维变换, M是在区间[-t, t]2内所有微小平移变化的集合。t选取的越大, 计算速度会越快, 但函数的区分度会明显下降, 实际中, 在一幅640×480的图像中一般取t=7, 此时可达到很好的平衡。
1.3 仿射投影变换经过前述步骤, 生成的模板已具有对微小变形和微小平移的不变性, 这里对基于主导梯度方向匹配的目标识别算法的一个重要改进是使算法能多视角识别同一个三维物体, 在同一次模板匹配学习过程中, 利用仿射投影变换, 提取仿射不变特征量, 将同一个模板生成多个角度范围内的不同仿射变换模板, 在匹配识别阶段, 当摄像头运动中视角发生变化时, 利用相应的仿射变换模板完成模板匹配, 多角度识别同一个三维物体。
下面简要介绍一下仿射变换原理及基本模型。由于视角变化引起的二维平面图像的变形, 可以通过平面仿射变换来描述。仿射变换是空间直角坐标变换的一种, 它是一种二维坐标到二维坐标之间的线性变换, 最重要的性质是保持点的共线性(或共面性)以及保持直线的平行性, 其可以通过一系列的平移、缩放、翻转、旋转等变化以及其组合来实现[13-15]。
由于摄像机运动而从不同视角拍摄到的图像, 可以看作是两两发生了仿射变换。考虑仿射变换变换前图像上某一点u(x, y), 经过仿射变换映射为图像上的点为u(ax+by+e, cx+dy+f), 则仿射变换的数学模型可以描述为
| $ \left[{\begin{array}{*{20}{c}} u\\ v \end{array}} \right] = \left[{\begin{array}{*{20}{c}} a&b\\ c&d \end{array}} \right]\left[{\begin{array}{*{20}{c}} x\\ y \end{array}} \right] + \left[{\begin{array}{*{20}{c}} e\\ f \end{array}} \right]。$ |
仿射模型中共有6个参数, 可以通过3对模板匹配特征点进行求解:
| $ \left[{\begin{array}{*{20}{c}} x&y&0&0&1&0\\ 0&0&x&y&0&1 \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{m_1}}\\ {{m_2}}\\ {{m_3}}\\ {{m_4}}\\ {tx}\\ {ty} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} u\\ v \end{array}} \right]。$ |
通过摄像机运动过程中视角的变化来描述两幅图像之间的仿射关系模型, 记
| $ \mathit{\boldsymbol{A}} = \lambda \left[{\begin{array}{*{20}{c}} {\cos \psi }&{-\sin \psi }\\ {\sin \psi }&{\cos \psi } \end{array}} \right]\left[{\begin{array}{*{20}{c}} t&0\\ 0&1 \end{array}} \right]\left[{\begin{array}{*{20}{c}} {\cos \phi }&{-\sin \phi }\\ {\sin \phi }&{\cos \phi } \end{array}} \right]。$ | (3) |
将A表示为A=λR(ψ)TtR(ϕ), 其中λ>0, 经运算,矩阵A的行列式为λt, ϕ∈[0, 180°], R(ψ)表示旋转角度为ψ的平面旋转矩阵, Tt表示倾斜度矩阵, ϕ和θ=arccos1/t是摄像机的观察视角, ψ表示摄像机自身的旋转角度。图 1是对式(3)摄像机运动的几何描述。
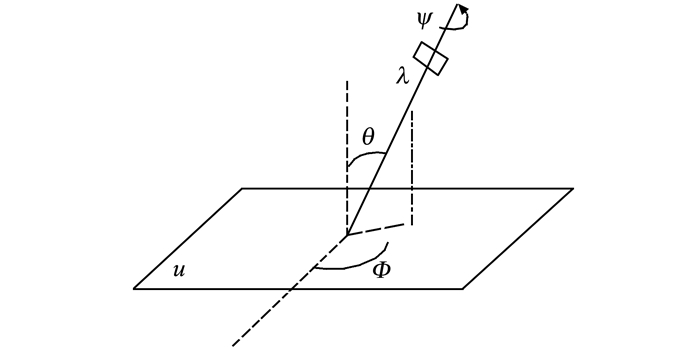
|
图 1 摄像机运动几何模型 Figure 1 Motion geometry model of camera |
在这个几何模型中, 摄像机在远离平面对象的位置。首先摄像机从平行于物体所在平面的正面位置开始运动。摄像机运动过程中, 物体平面u的法线和光轴平面所成平面与u的固定垂直平面所成角度ϕ, 这个角度叫做经度。光轴与平面法线的夹角为θ, 这个角度叫做纬度。倾斜度t≥1是通过t cos θ=1定义的。摄像机可以绕着它的光轴旋转, 旋转角度为ψ。最后一个参数是摄像机前后移动的变焦参数λ。总而言之, 式(3)中描述的仿射变换过程可概括为图像平面从u(x, y)→u(A(x, y))的变化过程, 对应摄像机从平行于物体平面时的位置λ0=1, t0=1, ψ0=ϕ0=0, 到有一定的由参数λ, t, ψ, ϕ决定的倾斜角度的运动过程。
方程(3)定义的是一种绝对倾斜, 即摄像机从平行于物体平面的正面位置到一定倾斜角度引起的图像的变形率。但对于从摄像机的两个不同倾斜位置获得两幅图像u1(x, y)=u(A(x, y))和u2(x, y)=u(B(x, y))。定义相对倾斜τ(u1, u2)和相对旋转ϕ(u1, u2), 这样可将相对倾斜定义为BA-1=HλR1(ψ)TτR2(ϕ)。图 2和图 3所示为相对倾斜的几何模型。
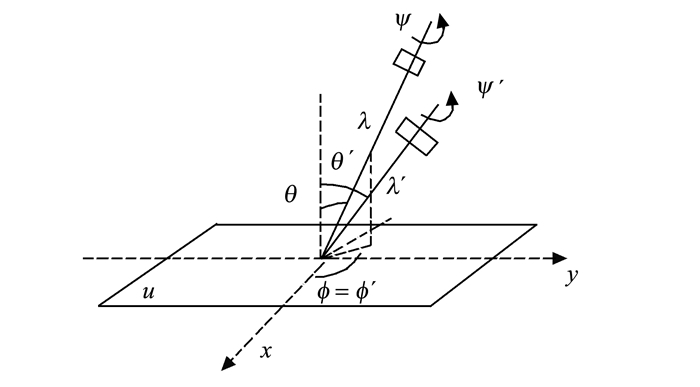
|
图 2 Φ不变的相对倾斜 Figure 2 Relative tilt by Φ unchanged |
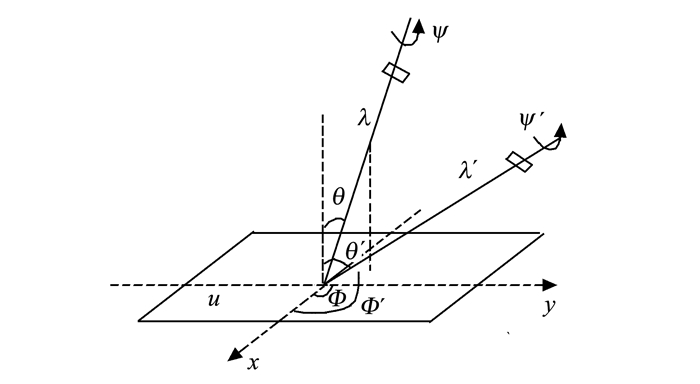
|
图 3 Φ变化的相对倾斜 Figure 3 Relative tilt by Φ changed |
经过上述仿射投影变换, 就可以在同一次基于主导梯度方向模板匹配的学习过程中, 通过设定摄像机不同的旋转角度ψ和观察角度ϕ、θ, 生成一个模板的同时产生多个角度范围内的不同仿射变换模板[16-17]。
2 分支界定聚类 2.1 二进制位表示法高效匹配为了高效快速地计算相似度函数ε4, 受文献[6]启发, 将链表L(O, R)和主导梯度方向函数do(I, c+R)表示为二进制形式, 仅通过简单的二进制按位操作运算计算相似度函数ε4, 计算过程如图 4所示。通常设置梯度离散方向的数目n0=7, 2×2的每一个小区域R的链表函数L(O, R)和主导梯度方向函数do(I, c+R)表示为8个二进制位, 前7位对应不同的梯度方向, 第8位代表⊥。
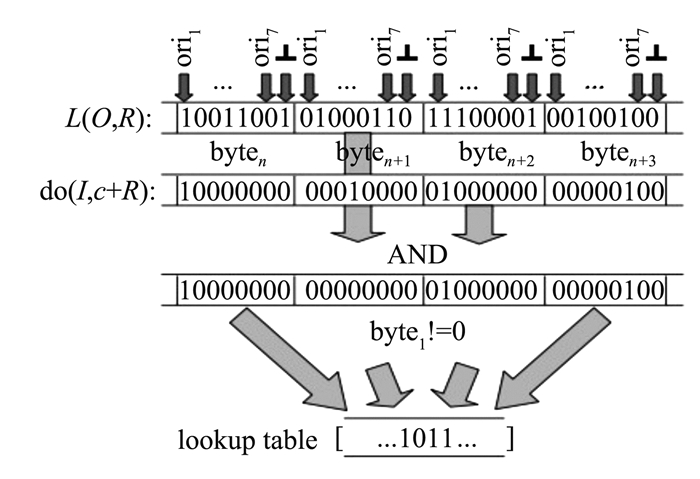
|
图 4 利用二进制位表示法计算相似度函数ε4 Figure 4 Schematic of similarity function calcultionby binary representation |
对于每一个链表L(O, R)对应的二进制位的一个字节L, 当i∈L(O, R)时, 对应的第i位将被置为1, 其中0≤i≤6;如果⊥∈L(O, R), 对应的第8位被置为1。而对于主导梯度方向特征do(I, c+R)对应的二进制位的一个字节D, 其中仅有一位被置为1。此时, 式(1)中的式子δ(do(I, c+R)∈L(O, R)))可等价为
| $ \delta \left( {{\rm{do}}\left( {I, c + R} \right) \in L\left( {O, R)} \right)} \right) = 1\;{\rm{if}}\;L \otimes \;D \ne 0, $ | (4) |
式中⊗表示按位与操作。
模板匹配的运算法则如图 4所示, 计算模板图像每一个小区域R的梯度方向链表L(O, R)与输入图像I的局部区域R的主导梯度方向二进制与运算后, 构建链表, 计算在区域R中相同的1的个数, 然后统计一个大块字节中1的个数。得到最多1的输入图像I的位置就是模板匹配的目标物体位置[18-19]。
2.2 分支界定聚类方法将DOT算法进一步扩展判断不同物体在不同视角下的不同模板之间的相似性。通常的想法是, 构建相似类模板, 每一个类用类模板来表示, 并对属于同一个类的类模板之间进行二进制与运算。该方法能提供严格的上限值, 并能用于分支界定法来完成有效搜索聚类[20-22]。首先通过实时计算输入图像I和类模板之间的相似性度量函数ε4, 过滤掉与当前输入图像I不相似的类模板。然后, 采用自下而上聚类方法, 为建立一个类, 在所有不属于某一个类的模板中随机抽取一个模板, 并反复迭代搜索模板T, 具体实现为
| $ \mathop {\arg \min }\limits_{T \ne {\rm{Cluster}}\;i} \max \left( {{d_h}\left( {C\;{\rm{or}}\;T, T} \right), {d_h}\left( {C\;{\rm{or}}\;T, C} \right)} \right), $ |
式中:dh是Hamming距离, or代表按位或操作, C代表进行按位与操作之前的类模板。整个过程要反复迭代进行, 直至训练出已知数目的类或所有模板T都搜索完, 这样就能不断把相类似的模板归为一类, 从而建立不同的类[20-22]。这种方法比二叉树聚类法速度更快, 可以完成在线实时聚类分析。
3 试验结果与分析为了验证基于主导梯度方向匹配的模板匹配算法的鲁棒性, 试验部分采用的不是标准数据集, 而是自己制作的数据库。数据集是在实际场景中用摄像头拍摄的实时数据, 采用罗技网络摄像头C901, 视频流采集分辨率是640×480, 采集到的数据没有做任何预处理, 对算法要求更高。该数据库包含了实验室常见物体, 如鼠标、水杯等纹理不丰富的物体。为了验证鲁棒性, 本研究对同一物体旋转、平移、弯曲后进行验证, 同时对多个物体进行识别验证, 并多视角进行验证。
3.1 试验效果本研究利用的目标识别算法是一种基于主导梯度方向匹配的模板匹配方法, 能实时在线多视角识别同一个物体, 也能同时识别多个不同物体, 对物体发生微小形变和微小平移时识别的鲁棒性很强, 不同光照条件下识别的稳定性强。下面将通过试验证明算法的可靠性。
(1) 识别不同物体
首先是对杂乱背景下不同目标物体进行识别, 图 5中绿色框区域为待识别物体的模板匹配边缘轮廓, 图 6中绿色框为对应的待识别物体所在的位置进行标记。试验证明, 待识别的物体经过在线快速地模板特征匹配后, 能很好地被识别出来。特别是对于纹理不丰富的物体, 识别效果也很好, 有效解决了基于特征点提取和匹配的算法(SIFT, SURF等)对纹理不丰富物体无法识别的问题。

|
图 5 杂乱背景下不同物体模板匹配结果 Figure 5 Object's edge outline of template matching ina clutter background |

|
图 6 杂乱背景下不同物体识别结果 Figure 6 Recognition results of different objects ina clutter background |
(2) 同一物体旋转、平移、弯曲
进行同一个物体在线识别过程中, 位置发生微小偏移或形变时的试验, 识别效果如图 7所示。

|
图 7 同一物体旋转、平移、弯曲试验效果 Figure 7 Objects detection results with rotation and motion |
(3) 同时识别多个不同物体
通过在线多次模板匹配学习, 可以同时识别多个不同物体, 识别效果如图 8、9所示。

|
图 8 多物体同时识别效果 Figure 8 The effect of multiple objects at the same time identify |

|
图 9 多物体同时匹配效果 Figure 9 Multiple objects at the same time the effect of matching |
(4) 多视角识别同一个三维物体
多个视角识别同一个三维物体的第一组试验是利用多次模板匹配学习完成的。在同一次试验中, 分别对图 10中便签本的(a)(b)(c)(d)四个侧面进行在线模板学习和匹配, 然后标记出匹配后的物体位置。

|
图 10 待识别物体不同侧面图像 Figure 10 Different side of the objects to be identified |
图 11所示为相应的模板匹配结果, 图 12所示为相应的侧面识别结果, 根据学习结果, 当装有摄像头的移动机器人再次从便签本的不同侧面靠近目标时, 会标记出目标的位置所在。

|
图 11 4个不同侧面的在线模板匹配结果 Figure 11 Online identification results of four different aspects |

|
图 12 4个不同侧面在线的识别结果 Figure 12 Online identification results of four different side |
第二组试验是在同一次模板匹配学习过程中, 利用仿射投影变换, 将同一个模板生成多个角度范围内的不同模板, 如图 13所示为图 10中(a)图仿射变换的例子。当摄像头运动中视角发生变化时, 利用相应的仿射变换模板完成模板匹配, 识别出物体, 如图 14所示为几种角度的识别结果。

|
图 13 几种仿射变换效果 Figure 13 Effects of some affine transformation templates |

|
图 14 多角度识别结果 Figure 14 Recognition results from different perspectives |
该程序运行的计算机的配置是:英特尔奔腾处理器E2180主频2 GHz, 内存1G DDR2 800。在这样的硬件环境下, 提取模板特征平均需要0.71 s, 识别阶段摄像头采集帧率13帧/s。
4 结论本研究采用一种改进型模板匹配算法, 不用耗时很长的离线训练过程, 能简便表示模板特征, 并针对该模板特征的表示方法, 设计了基于分支界定法的快速模板匹配过程。在应用过程中进行了大量试验, 模板匹配速度快, 因此物体识别速度快, 识别成功率也较好, 并且具有很好的在线学习功能, 能实时识别新物体。
主要的算法过程是结合了提取图像梯度的相似性度量法和鲁棒性很强的梯度直方图HOG法, 采用梯度这种形状特征进行匹配, 但不同于HOG算法的是, 去除次要的梯度特征, 只采用主要的幅度大的梯度进行匹配, 使得这种方法在识别纹理较少的物体时效果较好, 并且通过将模板二进制化提高速度, 使得算法能在线实时识别多个物体、并能多视角识别三维物体。
| [1] |
梅雪, 张继法, 许松松, 等. 分级特征提取与选择及在自动目标识别系统中的应用[J].
遥感技术与应用, 2012, 27(5): 712-715 MEI Xue, ZHANG Jifa, XU Songsong, et al. Hierarchical feature extraction and selection method and the applications in automatic target recognition system[J]. Remote Sensing Technology and Application, 2012, 27(5): 712-715 DOI:10.11873/j.issn.1004-0323.2012.5.712 |
| [2] |
孔金生, 张小凤, 王璇. 基于轮廓特征的模板匹配方法及其应用[J].
计算机工程与应用, 2008, 44(22): 201-203 KONG Jinsheng, ZHANG Xiaofeng, WANG Xuan. Template matching algorithm based on contour-feature and its application[J]. Computer Engineering and Applications, 2008, 44(22): 201-203 DOI:10.3778/j.issn.1002-8331.2008.22.060 |
| [3] |
周晨卉, 王生进, 丁晓青. 基于局部特征级联分类器和模板匹配的行人检测[J].
中国图象图形学报, 2010, 15(5): 824-829 ZHOU Chenhui, WANG Shengjin, DING Xiaoqing. Pedestrian detection based on partial feature and model matching[J]. Journal of Image and Graphics, 2010, 15(5): 824-829 DOI:10.11834/jig.20100518 |
| [4] |
刘忠红, 储珺. 特征提取与模板匹配结合的图像拼接方法[J].
微计算机信息, 2010, 26(1): 117-118 LIU Zhonghong, CHU Jun. A method for image mosaic based on combining feature extraction with template matching[J]. Control & Automation, 2010, 26(1): 117-118 |
| [5] | STEGER C. Occlusion, clutter, and illumination invariant object recognition[J]. B Radig & S, 2002, 34: 148-154 |
| [6] |
李志军, 刘松林, 牛照东, 等. 基于梯度相位和显著性约束的Hausdorff距离模板匹配方法[J].
红外与激光工程, 2015, 44(2): 775-780 LI Zhijun, LIU Songlin, NIU Zhaodong, et al. Hausdorff distance template matching method based on gradient phase and significance constraints[J]. Infrared and Laser Engineering, 2015, 44(2): 775-780 |
| [7] |
肖传民, 史泽林, 刘云鹏. 引入梯度分布特征的图像背景杂波度量[J].
光学精密工程, 2015, 23(12): 3472-3479 XIAO Chuanmin, SHI Zelin, LIU Yunpeng. Metrics of image background clutter by introducing gradient features[J]. Optics and Precision Engineering, 2015, 23(12): 3472-3479 |
| [8] | GRABNER M, GRABNER H, BISCHOF H. Tracking via discriminative online learning of local features[C]//Proceedings of the 2007 IEEE Computer Vision and Pattern Recognition. Minneapolis, USA: IEEE, 2007. |
| [9] | HINTERSTOISSER S, LEPETIT V, ILIC S, et al. Dominant orientation templates for real-time detection of texture-less objects[C]// Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco, USA: IEEE, 2010: 2257-2264. http://doi.ieeecomputersociety.org/10.1109/CVPR.2010.5539908 |
| [10] |
王国刚, 史洪岩, 汪滢, 等. 仿射不变子空间特征及其在图像匹配中的应用[J].
红外与激光工程, 2014, 43(2): 659-664 WANG Guogang, SHI Hongyan, WANG Ying, et al. Affine invariant subspace feature and its application in image matching[J]. Infrared and Laser Engineering, 2014, 43(2): 659-664 |
| [11] |
王红艳, 高尚兵. 基于全局和局部特征融合的显著性提取方法[J].
数据采集与处理, 2014, 29(5): 801-808 WANG Hongyan, GAO Shangbing. Saliency detection based on fusion of global and local features[J]. Journal of Data Acquisition & Processing, 2014, 29(5): 801-808 |
| [12] |
邹明明, 卢迪. 基于改进模板匹配的车牌字符识别算法实现[J].
国外电子测量技术, 2010, 29(1): 59-61 ZOU Mingming, LU Di. Recognition algorithm of car license plate characters based on modified template match[J]. Foreign Electronic Measurement Technology, 2010, 29(1): 59-61 |
| [13] | DEGUILLAUME F, VOLOSHYNOVSKIY S V, PUN T. Method for the estimation and recovering from general affine transforms in digital watermarking applications[J]. Proceedings of Spie, 2002, 4675(1): 313-322 |
| [14] | CEVIKALP H, TRIGGS B. Visual object detection using cascades of binary and one-class classifiers[J]. International Journal of Computer Vision, 2012, 123(10): 1-16 |
| [15] | FERRARI V, TUYTELAARS T, GOOL L V. Real-time affine region tracking and coplanar grouping[C]//Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Kauai, USA: IEEE, 2001(2): 226-233. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=990964 |
| [16] | BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features[J]. Computer Vision & Image Understanding, 2008, 110(3): 404-417 |
| [17] | LOWE D G. Object recognition from local scale-invariant features[C]//Proceedings of the IEEE International Conference on Computer Vision. Kerkyra, Greece: IEEE, 1999(2): 1150-1157. http://dl.acm.org/citation.cfm?id=851523 |
| [18] | COMANICIU D, RAMESH V, MEER P. Kernel-based object tracking[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2003, 25(5): 564-575 |
| [19] | MATTHEWS I, ISHIKAWA T, BAKER S. The template update problem[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2004, 26(6): 810-815 |
| [20] |
李博涛, 王之琪, 王秀彩. 分支界定法在特征向量提取中的应用[J].
山西电子技术, 2011(2): 37-38 LI Botao, WANG Zhiqi, WANG Xiucai. The appication of branch and bound algorithm in eigenvector selection[J]. Shanxi Electronic Technology, 2011(2): 37-38 |
| [21] | TAYLOR S, DRUMMOND T. Multiple target localization at over 100 FPS[C]// British Machine Vision Conference, BMVC 2009-Proceedings. London, UK: BMVA. 2009: 1-11. http://www.researchgate.net/publication/221260101_Multiple_Target_Localisation_at_over_100_FPS |
| [22] | LAMPERT C, BLASCHKO M, HOFMANN T. Beyond sliding windows: object localization by efficient subwindow search[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR). Anchorage, USA: IEEE, 2008: 1-8. http://doi.ieeecomputersociety.org/10.1109/CVPR.2008.4587586 |




