0 引言

在利用全球卫星导航系统(global navigation satellite system, GNSS)定位方面, 最常见的是测码伪距单点定位, 至少需要利用四颗卫星的伪距观测值进行单点定位, 其定位精度最优只能达到2.5m左右。为了获得更高的定位精度, 人们提出了差分定位技术。实时局域差分定位是建立在基准站和用户站对GNSS卫星的同步观测的基础上, 由于误差的时空相关性, 限制了基准站和用户站之间的距离, 因此客户的应用范围具有局限性。广域增强差分定位利用地球同步卫星转发差分改正信息给用户, 如美国广域差分增强系统(wide area augmentation system, WAAS)、欧洲导航重叠服务(European geostationary navigation overlay service, EGNOS)、日本多功能卫星增强系统(multi-functional satellite augmentation system, MSAS)等, 但该类增强系统对提高我国绝大部分卫星应用场景的定位精度帮助不大。此外, 美国天宝、荷兰辉固等公司也都推出了提供全球商业应用服务的广域增强差分系统, 中国航天科技集团也正在着手建设基于北斗的星基增强差分系统, 但是此类差分服务需要用户付费使用, 提高了用户成本, 目前仅大量应用于海洋勘探等部分特殊行业应用领域。

随着现代测量技术的发展, 人们提出了实时动态相位差分定位(real time kinematic, RTK)技术, 流动站利用基准站播发的载波相位差分改正信息进行厘米级实时动态定位, 但瓶颈仍然在于用户站的作业距离与基准站不能过长。进而提出了非差精密单点定位(precise point positioning, PPP)技术, 它是利用事先确定的精密卫星星历及精密卫星钟差, 与多频GNSS接收机采集的非差相位数据一起, 进行单点定位解算, 虽然其定位精度可以达到10cm的全球实时动态定位^[1], 但必须采用多频GNSS接收机, 对用户硬件成本要求高, 而且收敛时间长, 同样不能满足低成本实时精准定位的广泛应用需求。

随着智慧城市、智能交通、智慧海洋、精准农业等概念的提出, 高精度定位成为目前定位技术发展的主要趋势, 传统米级位置应用逐渐向亚米级位置服务升级, 同时对接收机的硬件成本也提出了更高的要求。因此为了满足车道级导航、地物采集、地质勘查、电力巡检、应急救援和海洋应用等对于亚米级定位的广泛需求, 研制低成本、稳定可靠、快速收敛的广域实时亚米级定位技术尤为迫切和重要。

1 广域实时亚米级定位算法

广域差分定位技术的基本思想是对GNSS定位中的与卫星有关的误差、与接收机有关的误差和与信号传播过程中产生的误差等主要误差源加以细分, 并分别加以“模型化”, 计算每一类误差修正值, 然后通过数据通讯链路传输给用户, 对用户GNSS接收机的观测值误差加以改正, 以削弱这些误差源的影响, 达到提高用户定位精度的目的。典型的广域差分定位技术如实时动态码相位差分(real time differential, RTD), 目前正广泛应用于千寻位置网络有限公司等商业公司推出的亚米级高精度定位服务中, 依托密集分布于全国的地基增强基准站, 综合利用各种定位技术, 提供互联网形式的差分位置数据播发平台, 首先获取用户接收机终端的RMC概略位置, 通过RTCM(radio technical committee for marine services)协议^[2]播发相应的差分改正信息给终端, 由终端接收机进行差分校正, 进而获得亚米级的定位结果。

本研究提出的广域亚米级定位算法不同于传统的RTD定位, 原理为基于单频GNSS接收机提供的卫星原始观测数据, 通过通讯链路获得IGS播发的卫星精密轨道和钟差改正数据求得卫星精确位置, 结合电离层格网改正模型^[3]及其他误差改正模型^[4], 利用载波平滑后的伪距定位模型^[5-6], 由终端嵌入式软件或APP软件的算法程序进行定位解算得到用户精确位置。以单频接收机的成本, 提供介于伪距单点定位的米级和精密差分单点定位的厘米级^[1]之间的亚米级的定位精度, 不存在收敛时间, 满足用户实时连续亚米级的定位需求。经过大量试验数据统计分析表明, 本算法在实时静态环境下, 全天候任意时段内均可实现平面方向优于0.8m、高程方向优于2m的定位精度。

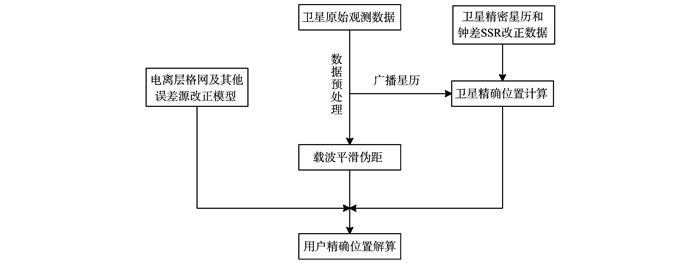
本算法部分源码参考RTKLIB软件^[7]实现, 流程示意图如图 1所示。

相比于常见的RTD和RTK定位技术, 本算法具有如下创新点和优势:

(1) 系统建设成本低, 无需大规模建设基准站, 全国范围内建设数十个基准站的情况下, 就可以满足全国范围内的亚米级定位应用需求。

(2) 采用载波平滑伪距的定位模型, 对网络播发的精密轨道和钟差改正信息在参考时间上不需要严格的时间同步, 无收敛时间^[8]。

(3) 基于实时的精密轨道和钟差改正数据, 满足亚米级定位的同时, 还可以同步实现用户测站的精准测速。

(4) 因为电离层误差无法利用差分源进行消除, 所以同样利用播发的精准电离层格网改正数据来消除电离层误差^[3], 提高定位精度。

(5) 本算法同时综合利用了对流层延迟改正模型、卫星和接收机天线相位中心改正模型、相对论效应、地球固体潮改正模型、海洋负荷潮改正模型、极潮改正模型等策略对误差源进行建模和消除^{[6, 9-10]}, 以消除各种误差影响, 提高定位精度。

2 基于SSR改正的卫星精密轨道和钟差计算

由于周跳探测方法^[11]、载波平滑伪距^[5-6]、最小二乘法^[9]等数学模型比较常见, 在此不再详细赘述, 本章主要介绍利用SSR(state space representation)改正的主要误差源卫星轨道误差和钟差误差的消除方法。

作为RTCM的开放标准之一的SSR信息格式, 是一种状态空间表示方法, SSR信息可以对GNSS的实时卫星轨道误差和钟差误差等误差源进行表述, 相比于观测空间表示方法OSR(observation space representation), SSR更适合用于GNSS单点定位的误差改正^[12]。

NTRIP协议(networked transport of RTCM via internet protocol)也是RTCM标准之一, 用于在Internet上传输RTCM 2.x及3.x格式的GNSS数据流, 在各种形式的高精度定位技术中, 基准站和流动站接收机之间的数据传输普遍采用该协议^[13]。

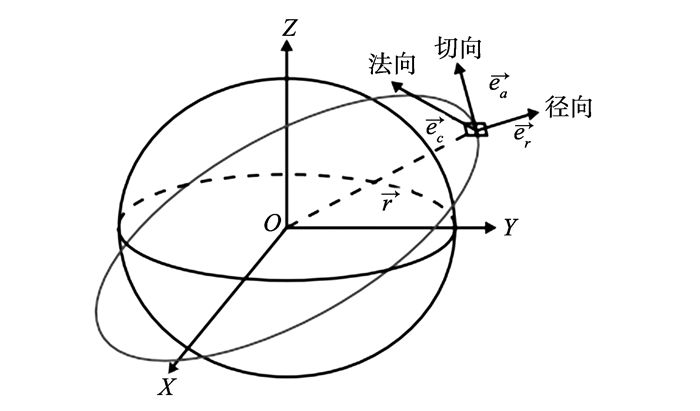
2.1 精密卫星轨道改正

SSR改正信息给出的卫星轨道误差是相对于卫星的广播星历来说的, 在计算卫星位置时, 根据SSR信息中提供的参数星历数据龄期IOD, 选择广播星历中相对应时刻的一组卫星轨道参数。SSR改正值分别给出了卫星径向、切向和法向三个方向上卫星位置及速度的改正值。其中, 切向与卫星速度向量方向一致, 法向垂直于由卫星位置向量和速度向量构成的平面, 径向与切向、法向相互垂直, 三者形成右手系^[14]。

假设SSR信息在$t_{0}$参考时刻提供的卫星位置改正向量为$\bar{\boldsymbol{d}}=[d_{r}~~d_{a}~~d_{c}]^{\text{T}}$、卫星速度改正向量为$\vec{\dot{\boldsymbol{d}}}=[{\dot{d}}_{r}~~{\dot{d}_{a}}~~{\dot{d}_{c}}$]$^{\text{T}}$, 则相对于观测时刻$t$, 对应的卫星位置改正向量$\vec{\mathbf{δ}}$表示为

$\begin{eqnarray} \vec{\mathbf{δ}}=\left[\begin{array}{c}δ_{r}\\δ_{a}\\δ_{c}\end{array}\right]=\left[\begin{array}{c}d_{r}\\d_{a}\\d_{c}\end{array}\right]+\left[\begin{array}{c}\dot{d}_{r}\\\dot{d}_{a}\\\dot{d}_{c}\end{array}\right](t-t_{0})。\end{eqnarray}$

(1)

假设由广播星历计算出的卫星位置向量为$\vec{\boldsymbol{r}}$=[$\begin{array}{c}X_{b}&Y_{b}&Z_{b}\end{array}$]$^{\text{T}}$, 由于卫星位置向量$\vec{\boldsymbol{r}}$和SSR卫星位置改正向量$\vec{\mathbf{δ}}$分别属于不同的参考坐标系。因此需要进行坐标转换, 将卫星轨道坐标系中的改正向量$\vec{\mathbf{δ}}$转换到地心地固坐标系$O$-$XYZ$中。由图 2所示, 假设$\vec{\dot{\boldsymbol{r}}}$为$O$-$XYZ$坐标系下表示的卫星速度向量, 可以求得$O$-$XYZ$坐标系中的单位向量$\vec{\boldsymbol{e}}$=[$\begin{array}{c}\boldsymbol{e}_\vec{r} &\vec{\boldsymbol{e}_{a}} &\vec{\boldsymbol{e}_{c}}\end{array}$], 其中$\vec{\boldsymbol{e}_{a}}=\frac{\vec{\dot{\boldsymbol{r}}}}{|\vec{\dot{\boldsymbol{r}}}|},\vec{\boldsymbol{e}_{c}}=\frac{\vec{\boldsymbol{r}}×\vec{\dot{\boldsymbol{r}}}}{|\vec{\boldsymbol{r}}×\vec{\dot{\boldsymbol{r}}}|},\vec{\boldsymbol{e}_{r}}=\vec{\boldsymbol{e}_{a}}×\vec{\boldsymbol{e}_{c}}。$

假设转换后的SSR卫星位置改正向量为$\vec{\mathbf{γ}}$, 则其可以表示为

$\begin{eqnarray} \vec{\mathbf{γ}}=\left[\begin{array}{c}γ_{X}\\γ_{Y}\\γ_{Z}\end{array}\right]=\left[\begin{array}{c}\boldsymbol{e}_\vec{r}&\vec{\boldsymbol{e}_{a}}& \vec{\boldsymbol{e}_{c}}\end{array}\right]\left[\begin{array}{c}δ_{r}\\δ_{a}\\δ_{c}\end{array}\right]。\end{eqnarray}$

(2)

因此, 在观测时刻$t$, 经SSR信息改正后的卫星位置向量表示为$\vec{\mathbf{ξ}}$=[$\begin{array}{c}X_{s}&Y_{s}&Z_{s}\end{array}$]$^{\text{T}}$, 则有

$\begin{eqnarray} \vec{\mathbf{ζ}}=\vec{\boldsymbol{r}}-\vec{\mathbf{γ}}=\left[\begin{array}{c}X_{s}\\Y_{s}\\Z_{s}\end{array}\right]=\left[\begin{array}{c}X_{b}\\Y_{b}\\Z_{b}\end{array}\right]-\left[\begin{array}{c}γ_{X}\\γ_{Y}\\γ_{Z}\end{array}\right]。\end{eqnarray}$

(3)

2.2 精密卫星钟差改正

对于卫星钟差改正, SSR信息给出了在参考时刻$t_{0}$用于计算卫星钟差多项式的3个系数, 即$C_{0}$、$C_{1}$、$C_{2}$, 因此就可以此系数计算在观测时刻$t$的卫星钟差改正值为

$\begin{eqnarray} Δk=C_{0}+C_{1}(t-t_{0})+C_{2}(t-t_{0})^{2}。\end{eqnarray}$

(4)

假设在观测时刻$t$, 由广播星历计算的卫星钟差表示为$Δt_{b}$, 改正后的卫星钟差表示为$Δt_{s}$, 则有

$\begin{eqnarray} Δt_{s}=Δt_{b}-\frac{Δk}{V_{c}} , \end{eqnarray}$

(5)

其中$V_{c}$代表真空中的光速。

3 试验结果与精度分析

武汉大学GNSS中心研究小组综合利用IGS中心和国际全球连续监测评估系统(international GNSS monitoring and assessment system, iGMAS)等全球连续监测评估系统的遍及全球的跟踪站数据, 利用多种高精度数学模型, 自主研发的实时卫星精密轨道和钟差改正产品已经成功应用于实时卫星精密定轨和精密单点定位技术^[15-16]。为了充分对比验证本算法的良好定位性能, 本试验中, 卫星精密轨道和钟差及电离层格网改正数据从武汉大学GNSS中心所维护的NTRIP播发器中获取NTRIP数据源列表, 并分别选取稳定的挂载点CLK91和WUD实时接收RTCM-3格式的SSR二进制数据流, 其中CLK91挂载点播发的是IGS改正数据, WUD挂载点播发的是武汉大学研究小组自主研发的高精度定位改正数据。利用前文所述的广域亚米级定位算法和GNSS接收机普遍支持的RTD差分定位算法分别进行大量重复试验进行验证。

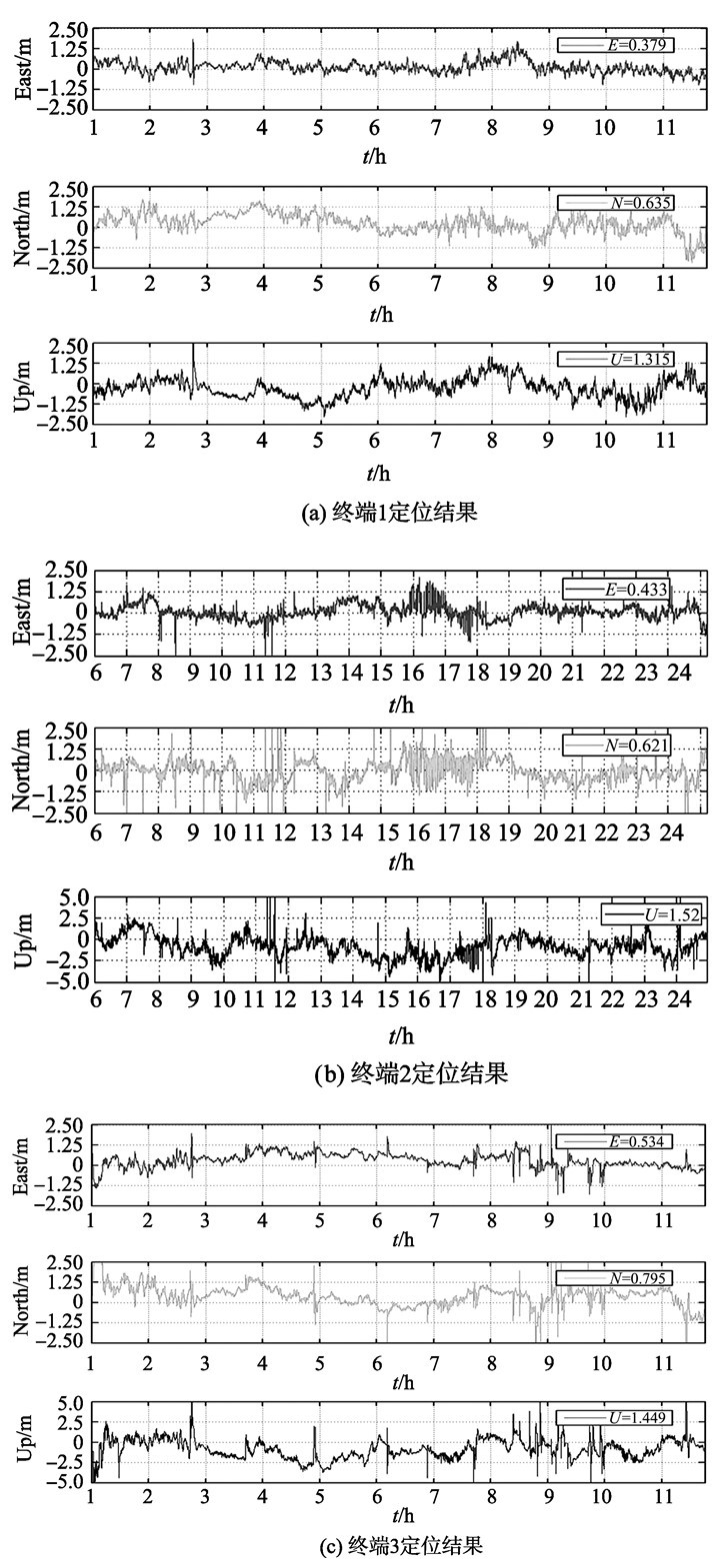
试验用硬件终端中的定位接收机选择由SkyTraq公司生产的S1216-F8-BD-RAW定位模块, 该模块既支持卫星原始RAW数据上传, 用于广域亚米级定位, 同时支持RTD改正数据接收进行RTD差分定位。接收机天线采用普通测量型天线通过功分器统一分配, 进行静态测试。终端1接收挂载点WUD播发的卫星改正数据, 运行本广域亚米级定位算法; 终端2接收挂载点CLK91播发的卫星改正数据, 运行本广域亚米级定位算法; 终端3通过千寻分配的账号进行连接, 接收由千寻位置网络有限公司服务器播发的RTD定位服务产品, 运行RTD差分定位算法。选取白天电离层活跃时段连续12小时的程序运行数据进行统计分析如图 3和表 1所示，其中纵坐标East、North、Up和变量$E$、$N$、$U$分别表示东、北、上三个方向的定位误差，均方根误差RMS又叫标准误差，它是观测值与真实值偏差的平方和观测次数n比值的平方根，用来指示定位误差。

由定位精度统计结果表明, 本研究提出的广域亚米级定位算法和千寻RTD服务均可以稳定提供平面精度优于1m、高程精度优于2m的位置信息; 广域亚米级定位算法因为利用卫星原始观测值和各种误差改正模型, 进行自主解算, 因此求得用户位置更加精确, 水平精度可以稳定在优于0.8m, 定位精度高于千寻RTD定位; 由于武汉大学自主播发的卫星精密轨道和钟差及电离层格网改正数据为自主研发, 选择利用了更多和更加精确的误差改正模型, 因此用于同一算法时, 定位精度优于基于IGS播发的改正产品的定位情形; 由于白天电离层明显比夜间活跃, 实际的试验结果也证明该广域亚米级定位算法在全天候任意时段内均可实现水平方向的亚米级定位精度。

4 结束语

本研究提出的广域实时亚米级定位算法, 在基于目前的资源条件下进行的静态对比测试结果中, 表现出实时稳定的亚米级单点定位精度, 研究结果可以广泛应用于车道级定位、地物采集、地质勘查、电力巡检、应急救援和海洋应用等行业领域。针对高速动态应用, 需要进一步研究辅助以惯性导航系统(inertial navigation system, INS)技术的组合导航定位系统, 可以达到稳定的实时的动态连续亚米级导航。同时在通信链路稳定的前提下, 如何提高算法的鲁棒性将是一个艰巨的课题。另外, 利用更多的误差改正模型和更加精确的改正数据源, 进一步提高本算法的定位精度, 也将是未来需要持续研究的工作。