0 引言

基于结构保持的流形学习算法, 将数据表示为嵌入高维空间的低维子流形, 其中确定数据的邻接图及权重矩阵是算法的关键。在无监督条件下, $K$-近邻是最简单常用的邻接图确定方法, 局部线性嵌入(locally linear embedding, LLE)和拉普拉斯特征映射(Laplacian eigenmap, LE)均采用这种方法构成邻接图, 前者利用每个样本的线性表示系数构成权重矩阵^[1], 后者通过计算相似度距离构成权重矩阵^[2]。但是这两种方法是非线性流形学习算法, 无法求出具体的投影矩阵。局部保留投影(locality preserving projections, LPP)算法是LE的线性扩展^[3], 将低维响应写成投影矩阵与训练样本的乘积, 可以求得显式的投影矩阵, 因此广泛应用于特征提取。另一方面, 为解决$K$-近邻的选取问题, 文献[4]提出一些自动确定邻接图的方法。稀疏保留投影(sparsity preserving projections, SPP)利用样本在除自身之外的训练样本上的稀疏表示系数构成权重矩阵^[5], 巧妙地同时解决近邻选取和权重赋值问题, 然而计算复杂度高。在文献[6]启发下, 文献[7]使用$l_{2}$范数正则化取代稀疏表示中的$l_{1}$范数正则化, 提出的协同表示投影(collaborative representation based projections, CRP)可有效降低计算复杂度, 但此时邻接图不具有稀疏性。无论是稀疏表示还是协同表示求出的系数是互相独立的, 无法反应样本在全局中的相互关系。

低秩表示直接对系数矩阵进行整体约束, 能够揭示数据的全局结构信息, 又具有一定的聚类效果^[8-10]。本研究使用低秩表示求解邻接图和权重矩阵, 提出低秩表示投影算法(low-rank representation projection, LRRP)。为了增强特征的鉴别能力, 引入低秩系数聚类后的类内距离约束项, 进一步提出鉴别低秩表示投影(discriminant low-rank representation projection, DLRRP)。在4个真实人脸数据库中进行比较试验, 结果说明本研究算法能有效提高人脸识别的正确率。

1 相关工作 1.1 线性保留投影

假设训练样本矩阵$\boldsymbol{X}$=[$\begin{array}{c}x_{1}&x_{2}&…&x_{m}\end{array}$]包含$m$张$n$维人脸图像, 其中每一列$\boldsymbol{x}_{i}$代表向量化后的第$i$张图像。将每个样本视为一个顶点, 构成邻接图$G$, 每对顶点之间有一条边连接, 边权重矩阵$\boldsymbol{W}$∈$\mathbf{R}^{m×m}$, 可以表示出一组数据之间的相互关系, $W_{ij}$表示点$\boldsymbol{x}_{i}$与$\boldsymbol{x}_{j}$间的边权重, 其数值计算分为有监督和无监督情况, 统一写作如下形式:

$ {W_{ij}} = \left\{ {\begin{array}{*{20}{c}} {非零值 \in \left( {0,1} \right]}&{连接条件}\\ 0&{其他} \end{array}} \right., $

(1)

在经典LPP算法中, 连接条件一般是这样设置的:有监督情况下, 条件为$\boldsymbol{x}_{i}$, $\boldsymbol{x}_{j}$具有同样标签; 无监督情况下, 条件为$\boldsymbol{x}_{i}$∈$N$($\boldsymbol{x}_{j}$)或者$\boldsymbol{x}_{j}$∈$N$($\boldsymbol{x}_{i}$), 其中$N$($\boldsymbol{x}$)表示$\boldsymbol{x}$近邻。非零值可定义为1、热核距离或者cosine距离等^[11]。LPP算法通过保留数据局部结构为准则, 将并且将投影矩阵$\boldsymbol{A}$显式包含在目标函数中:

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{A}} = \mathop {\arg \min }\limits_\mathit{\boldsymbol{A}} \sum\limits_{ij}^m {{{\left( {{\mathit{\boldsymbol{x}}_i}{\mathit{\boldsymbol{A}}^{\rm{T}}} - {\mathit{\boldsymbol{x}}_j}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)}^2}{W_{ij}}} = }\\ {\mathop {\arg \max }\limits_\mathit{\boldsymbol{A}} \frac{{{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{XD}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}}}}{{{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{XL}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}}}},} \end{array} $

(2)

式中: $\boldsymbol{D}$是一个对角矩阵; $d_{ii}=∑\limits_{j}W_{ij}$, 称为图的度矩阵; $\boldsymbol{L}$=$\boldsymbol{D}$-$\boldsymbol{W}$为拉普拉斯矩阵。很明显, 式(2)为一个最小广义特征值求解问题:

$ \mathit{\boldsymbol{XL}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} XD}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}}, $

(3)

投影矩阵$\boldsymbol{W}$由前$k$个最小特征值对应的特征向量构成，其中$k$是降维后的空间的维度。

不同于式(1), 自适应的选取$K$-近邻及其权值的算法中, $W_{ij}$是通过表示算法计算得到的, 在SPP中, 对$x_{i}$使用除它以外的人脸图像对其稀疏表示, 目标函数如下:

$ \begin{array}{l} {\mathit{\boldsymbol{\beta }}_i} = \mathop {\arg \min }\limits_{{\beta _i}} \left\| {{\mathit{\boldsymbol{X}}_i}{\mathit{\boldsymbol{\beta }}_i} - {\mathit{\boldsymbol{x}}_i}} \right\|_2^2 + \lambda {\left\| {{\mathit{\boldsymbol{\beta }}_i}} \right\|_1},\\ {\mathit{\boldsymbol{X}}_i} = \left[ {\begin{array}{*{20}{c}} {{x_1}}& \cdots &{{x_{i - 1}}}&0&{{x_{i + 1}}}& \cdots &{{x_m}} \end{array}} \right]。\end{array} $

(4)

在求第$i$个训练样本的表示系数为$\mathbf{β}_{i}$时, 第$i$个位置对应的是0向量, 即不使用样本对自己线性表示。基于投影之后的数据依然要保持稀疏重构关系的准则, SPP投影矩阵$\boldsymbol{A}$需最优化如下目标:

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{A}} = \mathop {\arg \min }\limits_\mathit{\boldsymbol{A}} \sum\limits_{i = 1}^m {{{\left\| {{\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{\beta }}_i}} \right\|}^2}} = }\\ {\mathop {\arg \min }\limits_\mathit{\boldsymbol{A}} {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{X}}\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{S}}} \right){{\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{S}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}} = }\\ {\mathop {\arg \max }\limits_\mathit{\boldsymbol{A}} {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{L}}_S}{\mathit{\boldsymbol{X}}^{\rm{T}}}A,} \end{array} $

(5)

式中: $\boldsymbol{S}$=[$\begin{array}{c}β_{1}&β_{2}&…&β_{m}\end{array}$]为权重矩阵, 它的每一列是由上一步稀疏表示求解出来的系数构成, $\boldsymbol{L}_{S}$=$\boldsymbol{S}$+$\boldsymbol{S}^{\text{T}}$-$\boldsymbol{S}\boldsymbol{S}^{\text{T}}$=$\boldsymbol{I}$-($\boldsymbol{I}$-$\boldsymbol{S}$)($\boldsymbol{I}$-$\boldsymbol{S}$)$^{\text{T}}$, 这同样可化为求解如下最大广义特征值的问题:

$ \mathit{\boldsymbol{X}}{\mathit{\boldsymbol{L}}_S}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} X}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}}。$

(6)

CRP与SPP的思想相同, 也是利用正则化的线性回归形式求出训练样本之间的相似关系, 不同的是, CRP使用$l_{2}$范数替代SPP中的$l_{1}$范数, 求第$i$个训练样本与其他样本的相似度系数的目标函数如式(7)所示, 该模型具有解析解, 大大减少了计算复杂度。

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\beta }}_i} = \mathop {\arg \min }\limits_{{\mathit{\boldsymbol{\beta }}_i}} \left\| {{\mathit{\boldsymbol{X}}_i}{\mathit{\boldsymbol{\beta }}_i} - {\mathit{\boldsymbol{x}}_i}} \right\|_2^2 + \lambda {{\left\| {{\mathit{\boldsymbol{\beta }}_i}} \right\|}_2},}\\ {{\mathit{\boldsymbol{X}}_i} = \left[ {\begin{array}{*{20}{c}} {{x_1}}& \cdots &{{x_{i - 1}}}&0&{{x_{i + 1}}}& \cdots &{{x_m}} \end{array}} \right]。} \end{array} $

(7)

使用总体散度矩阵($\boldsymbol{X}$-$\bar{\boldsymbol{X}}$)($\boldsymbol{X}$-$\bar{\boldsymbol{X}}$)$^{\text{T}}$替代$\boldsymbol{X}\boldsymbol{X}^{\text{T}}$防止解退化, CRP的目标函数等价为如下广义特征值问题:

$ \mathit{\boldsymbol{X}}{\mathit{\boldsymbol{L}}_c}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}\left( {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{\bar X}}} \right){\left( {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{\bar X}}} \right)^{\rm{T}}}\mathit{\boldsymbol{A}}, $

(8)

式中: $\boldsymbol{L}_{c}$=$\boldsymbol{S}$+$\boldsymbol{S}^{\text{T}}$-$\boldsymbol{S}\boldsymbol{S}^{\text{T}}$, 与SPP不同, CRP模型的系数不具有稀疏性。

1.2 低秩表示

低秩表示(LRR)可以有效地保留数据类别之间的差异性, 将其运用到图像聚类上, 可取得良好的效果^[12], 其数学模型为

$ \begin{array}{l} \min \;{\rm{rank}}\left( \mathit{\boldsymbol{Z}} \right)\\ {\rm{s}}.{\rm{t}}.\;\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{XZ}} + \mathit{\boldsymbol{\eta E}}, \end{array} $

(9)

式中：$\boldsymbol{Z}$是系数矩阵，$\boldsymbol{E}$是误差。

由于上述优化问题为NP-hard问题, 可以使用核范数替代秩数, 将其转化为凸优化问题:

$ \begin{array}{l} \min \;\;{\left\| \mathit{\boldsymbol{Z}} \right\|_ * } + \lambda {\left\| \mathit{\boldsymbol{E}} \right\|_{2,1}}\\ {\rm{s}}.{\rm{t}}.\;\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{XZ}} + \mathit{\boldsymbol{E}}。\end{array} $

(10)

2 判别低秩表示投影 2.1 低秩表示投影

为了利用LRR较强的全局信息提取能力和系数具有聚类效果的特点, 将其应用到局部保留算法中, 可以得到鲁棒性更强的自适应局部保留算法。首先对训练样本$\boldsymbol{X}$进行自身的低秩表示, 求解如下目标函数

$ \begin{array}{*{20}{c}} {\mathop {\min }\limits_\mathit{\boldsymbol{W}} \;\;{{\left\| \mathit{\boldsymbol{W}} \right\|}_ * } + \lambda {{\left\| \mathit{\boldsymbol{E}} \right\|}_{2,1}}}\\ {{\rm{s}}.{\rm{t}}.\;\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{XW}} + \mathit{\boldsymbol{E}},} \end{array} $

(11)

式中: $\boldsymbol{E}$为误差矩阵, $\boldsymbol{W}$为低秩表示系数。LRRP将$\boldsymbol{W}$=[$w_{1}$ $w_{2}$ … $w_{m}$]作为样本邻接关系的权重矩阵，并将该邻接关系保留在投影之后的空间里，设所有的投影为$\boldsymbol{A}$, 得到如下重构项优化目标:

$ \begin{array}{l} \mathop {\min }\limits_\mathit{\boldsymbol{A}} \sum\limits_i^m {{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{w}}_i}} \right)}^2}} = \\ \;\;\;\;\;\;\;\;\;\;\;\mathop {\min }\limits_\mathit{\boldsymbol{A}} \sum\limits_i^m {{\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{X}}{\mathit{\boldsymbol{w}}_i}} \right){{\left( {{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{X}}{\mathit{\boldsymbol{w}}_i}} \right)}^{\rm{T}}}\mathit{\boldsymbol{A}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\mathop {\min }\limits_\mathit{\boldsymbol{A}} {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{X}}\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{W}}} \right){\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{W}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}} = \\ \;\;\;\;\;\;\;\;\;\;\;\mathop {\max }\limits_\mathit{\boldsymbol{A}} {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{L}}}{\mathit{\boldsymbol{X}}^{\rm{T}}}A, \end{array} $

(12)

使用$\boldsymbol{A}^{\text{T}}\boldsymbol{X}\boldsymbol{X}^{\text{T}}\boldsymbol{A}$=$\boldsymbol{d}$来避免产生退化解, 化为最大广义特征值问题:

$ \mathit{\boldsymbol{X}}{\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{L}}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} X}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}}, $

(13)

式中: $\boldsymbol{L}_{L}$=$\boldsymbol{W}$+$\boldsymbol{W}^{\text{T}}$-$\boldsymbol{W}\boldsymbol{W}^{\text{T}}$=$\boldsymbol{I}$-($\boldsymbol{I}-\boldsymbol{W}$)($\boldsymbol{I}$-$\boldsymbol{W}$)$^{\text{T}}$。假设投影后维度为$k$($k$＜$n$), 按照从大到小的$k$个特征值对应的特征向量构成投影矩阵$\boldsymbol{A}$=[$\begin{array}{c}a_{1}&a_{2}&…&a_{k}\end{array}$], $\boldsymbol{Y}$=$\boldsymbol{A}^{\text{T}}\boldsymbol{X}$得到降维后的样本。

2.2 判别低秩表示投影

相比$l_{1}$范数和$l_{2}$范数正则化约束, LRR优势有两点:可以发现数据的全局性结构, 对噪声的鲁棒性更强。低秩表示本身对数据具有聚类的作用, 当已知样本的类别数目$C$时, 即使不知道具体的标签信息, 那么可以首先以低秩表示系数为相似度, 将样本进行聚类。若不知道类别数目, 可以采用吸引子传播算法(affinity propagation, AP)等无需预先进行确定$C$的算法进行聚类^[13]。本研究假定已知类别数目$C$, 通过聚类结果引入类内距离约束项到最小化的目标函数中, 增强投影的鉴别能力。鉴别项目标函数

$ \begin{array}{l} \min \sum\limits_k^C {\sum\limits_l^{{n_k}} {{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{x}}_l} - {\mathit{\boldsymbol{A}}^{\rm{T}}}{{\mathit{\boldsymbol{\bar x}}}_k}} \right)}^2}} } = \\ \;\;\;\;\;\;\min {\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{X}}^{\rm{T}}} - \sum\limits_k^C {{n_k}{{\mathit{\boldsymbol{\bar x}}}_k}\mathit{\boldsymbol{\bar x}}_k^{\rm{T}}} } \right)\mathit{\boldsymbol{A}} = \\ \;\;\;\;\;\;\min {\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{X}}^{\rm{T}}} + \mathit{\boldsymbol{XH}}{\mathit{\boldsymbol{X}}^{\rm{T}}}} \right)\mathit{\boldsymbol{A}} = \\ \;\;\;\;\;\;\min {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{L}}_1}{\mathit{\boldsymbol{X}}^{\rm{T}}}A, \end{array} $

(14)

式中: $n_{k}$表示第$k$类样本的个数; $\bar{\boldsymbol{x}}_{k}$表示第$k$类的样本均值; $\boldsymbol{H}$是块对角矩阵$\boldsymbol{H}=\text{diag}(\boldsymbol{H}_{1},\boldsymbol{H}_{2},…,\boldsymbol{H}_{C})$, 每个块$\boldsymbol{H}_{k}$是一个全部值为$1/n_{k}$的$n_{k}×n_{k}$矩阵; $\boldsymbol{L}_{1}=\boldsymbol{I}-\boldsymbol{H}$。综合考虑鉴别项及式(12)的重构项, $\text{DLRRP}$的目标函数

$ \begin{array}{*{20}{c}} {\mathop {\min }\limits_\mathit{\boldsymbol{A}} {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{X}}\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{S}}} \right){{\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{S}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \gamma {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{L}}_1}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}} = }\\ {\mathop {\min }\limits_\mathit{\boldsymbol{A}} {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{X}}\left[ {\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{S}}} \right){{\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{S}}} \right)}^{\rm{T}}} + \gamma {\mathit{\boldsymbol{L}}_1}} \right]{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}},} \end{array} $

(15)

式中:$γ$为平衡二者的参数。为了避免产生退化解^[14], 使用$\boldsymbol{A}^{\text{T}}\boldsymbol{X}\boldsymbol{X}^{\text{T}}\boldsymbol{A}$=$\boldsymbol{d}$对式(14)加以限制, 类似于式(13)的推导过程, 通过拉格朗日乘数法将式(15)转化为一个最大广义特征值求解问题:

$ \mathit{\boldsymbol{X}}\left( {2\mathit{\boldsymbol{S}} + \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{S}}^{\rm{T}}} - \gamma {\mathit{\boldsymbol{L}}_1}} \right){\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} X}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{A}}, $

(16)

将特征向量按照特征值从大到小的顺序排列可得到投影矩阵$\boldsymbol{A}$。

3 试验

将LRRP、DLRRP在AR^[15]、Extend YaleB(简记为YaleB)^[16]、FERET和CMU-PIE这4个真实人脸数据库中进行人脸识别^[17-18], 并与PCA、LDA、LPP、SPP、CRP方法进行比较。其中利用表示算法求权重矩阵的LPP、SPP、CRP及本研究算法中的系数正则化参数$λ$从{$\begin{array}{c}10^{-3}&10^{-2}&…&10^{3}\end{array}$}中选取最优值, DLRRP中的两项目标函数之间的平衡参数$λ$在[0, 1]中选取, 为加快计算, 试验中的数据首先进行PCA降维, 保留98%能量主成分的预处理^[19]。在特征空间中对测试样本进行分类, 各算法均采用基于欧氏距离的最近邻分类器^[20]。

3.1 AR人脸数据库

由于SPP运算量较大, 为了方便试验对比, 本研究只使用AR人脸数据库中的前100个对象进行试验, 每个对象26张人脸图像, 第一阶段的13张作为训练样本, 第二阶段的13张作为测试样本, 在每一阶段中, 前4张反应姿态变化, 5~7张处于不同光照, 8~13张存在面部遮挡。最高识别率及其对应的维度记录在表 1中, 不同维度对应的识别率展示在图 1中。

由表 1和图 1可知, LRRP的识别率比SPP和CRP高。而加入判别信息之后, 相比于LRRP, DLRRP的识别率有很大提高, 达到了78.38%, 稍高于LDA的76.67%, 说明低秩系数确实有助于提供图像的聚类信息, 构造的判别项即使在无标签信息情况下也会接近甚至优于有监督算法的LDA的识别率, 但DLRRP的最优识别率对应的维度大于LDA。需要说明的是, 在此试验中LRRP的识别率低于LDA, 这是因为LDA作为有监督的特征提取方法, 在训练样本比较充足的情况下要优于无监督算法。但是在图 1和表 1中可以看到, 在无监督条件下的算法中, LRRP的识别率高于SPP和CRP的。

研究低秩表示正则化参数$λ$的取值对LRRP和DLRRP识别率影响。当$λ$的值过小时, 式(14)倾向于寻找秩最低的投影, 这会导致信息的鉴别信息被减弱; 当$λ$的值过大时, 优化倾向于寻找重构性最好的投影。图 2展示了识别率随$λ$的变化情况, 当$λ$=0.1~1, 识别率较高, 在此范围内, 低秩表示的去噪能力和鉴别能力达到较为均衡的状态。所以, 低秩表示的参数$λ$设为1。

采用类似方法, 在[0, 1]寻找最优平衡参数$γ$。图 3显示的是AR库人脸图像在100维上的识别率的变化图, 可以看出当$γ$较小时, 由于引入监督信息, 识别率得到很大的提高, 但是当$γ$大于0.1之后, 识别率逐渐下降, 这是由于类间距离项所占比例过大的原因, 本研究选取$γ$=0.1。其他数据库对应的参数取值方法相同, 不再赘述。

3.2 Extended Yale B人脸数据库

Extended Yale B人脸数据库包含38个对象, 每个对象64张图片, 将其剪切为40×40大小。随机选取其中的32张图片作为训练样本, 剩余的32张图片作为测试样本, 测试20次, 取平均值, 每种方法对应的最高识别率如表 2所示。

从表 2可以看出, LRRP的识别率要高于SPP和CRP, 这种优势是源于LRR对于噪声的强鲁棒性和良好的全局信息提取能力, 由于缺乏监督信息, 在相同的维度下识别率略低于LDA。DLRRP引入类内距离最小化项, 利用系数的聚类信息, 相比于LRRP, 其识别率有较大提高, 略高于LDA。

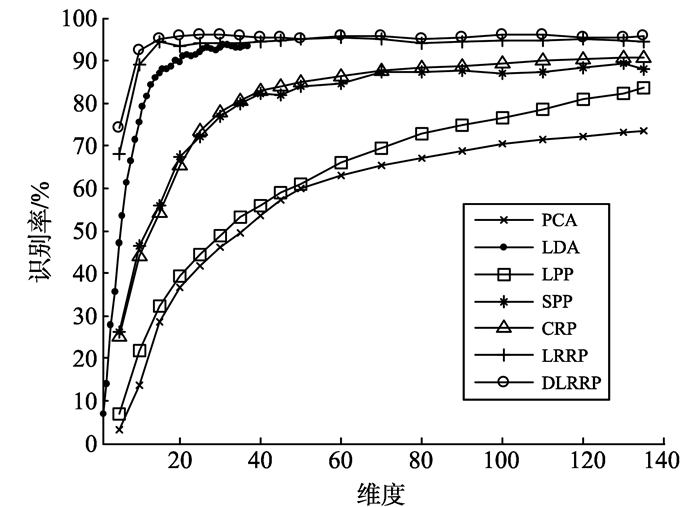
图 4展示各方法在Extended YaleB人脸数据库上, 维度对识别率的影响。

从图 4中可以看到低维度时LRRP的识别率远高于SPP和CRP。由于引入类内距离约束项, DLRRP的鉴别能力很强, 在维度很低时就能达到比较高的识别率, 略高于LDA和LRRP。

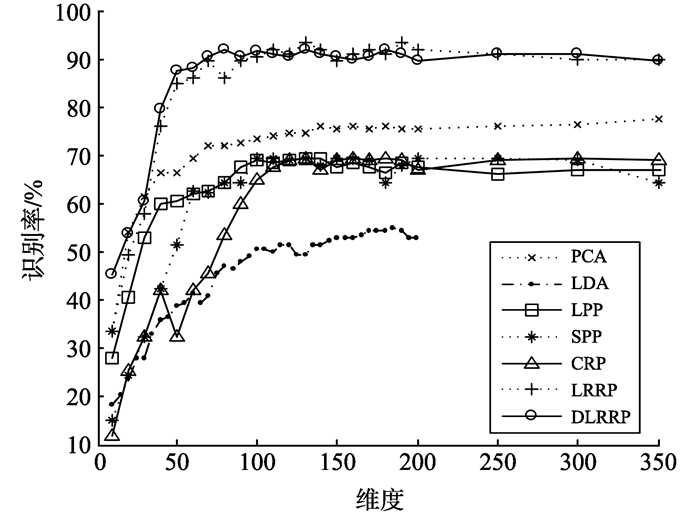
3.3 FERET人脸数据库

FERET人脸数据, 共200个对象, 每个对象7张人脸图片, 每张图片的大小为40×40, 取前6张人脸图片作为训练样本, 剩余的1张作为测试样本。各个算法的最高识别率记录在表 3中, 维度对于识别率的影响展示在图 5中。

从表 3和图 5中可以看出, LRRP的识别率最高, 略高于DLRRP, 比SPP和CRP高12%, 且远远高于PCA、LPP和LDA。DLRRP的鉴别能力低于LRRP是由于类内约束项在小样本情况下的不佳表现导致, 这种情况和LDA在小样本情况下存在的问题相似。在这个数据库中, 从LDA算法的结果看出, 由于人脸图像角度的变化是图像之间的最大差异, 即使在有监督的情况下, LDA也对角度变化的鲁棒性差。

3.4 CMU-PIE人脸数据库

CMU-PIE人脸数据库包含68个对象, 每个对象包括24张不同光照强度的人脸图像, 将其剪切为32×32大小。每类中随机选取8张人脸图片作为训练样本, 其余的16张人脸图像作为测试样本。表 4记录了各个算法的最高识别率。

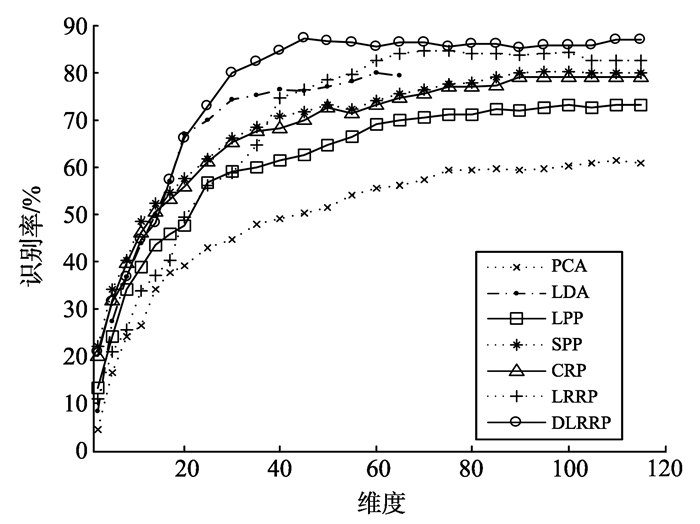
由表 4可以看到, DLRRP在最小降维维度就达到最优识别率, 且最优识别率比LRRP高3.78%, 进一步说明DLRRP的鉴别能力要优于LRRP。图 6展示各方法在CMU-PIE人脸数据库上, 特征维度对识别率的影响。由图 6可以看出, DLRRP识别率关于维度的快速收敛性。

4 结论

本研究利用低秩表示自适应地获得数据点的最近邻及权重矩阵, 提出LRRP和DLRRP算法进行人脸图像的特征提取。不同于稀疏表示和协同表示, 低秩表示系数包含全局结构信息, 对于噪声有很强的鲁棒性。将全部训练样本进行自身的低秩表示, 并将此种低秩表示关系保留在特征空间中, 建立LRRP目标函数。另一方面, 考虑低秩系数所反应的样本的聚类关系, 引入类内距离约束项, 进一步提出更加具有鉴别性的DLRRP。在AR、Extended Yale B、FERET和CMU-PIE人脸数据库中的试验表明, 低秩表示本身具有的聚类效果导致LRRP的鲁棒性更强, 鉴别能力相比于SPP和CRP也有提高; 由低秩表示所计算的最小化类内距离约束项确实有效增强DLRRP的鉴别能力。

本研究算法是线性方法, 通过核技术的引入可扩展为非线性特征提取算法; 另外在加入鉴别项时假设已知类别数目, 下一步将研究未知类别数目下的聚类算法在鉴别信息计算中的应用。

(下转第 ３０ 页)