2. 徐州市城区水资源管理处, 江苏 徐州 221018;
3. 中国矿业大学数学学院, 江苏 徐州 221116
2. Xuzhou City Water Resource Administrative Office, Xuzhou 221018, Jiangsu, China;
3. School of Mathematics, China University of Mining and Technology, Xuzhou 221116, Jiangsu, China
目前水质模型参数识别的方法主要有正则化方法[1]、模拟退火算法[2]、遗传算法[3]、微分进化算法(differential evolution, DE)[4-14]和贝叶斯-马尔科夫链蒙特卡罗算法(Bayesian and Markov Chain Monte Carlo, Bayesian-MCMC) [15-20]等。国内水污染事件反问题的研究较多。陈海洋等[21]运用Bayesian-MCMC实现了水体污染源项的识别; 杨海东等[22]结合DE算法的思想, 提出了微分进化蒙特卡罗方法(DE-MCMC), 用于解决二维河道突发水污染溯源问题; 闵涛等[23]利用遗传算法求解对流-扩散方程源项识别反题; 牟行洋[24]运用DE算法并结合有限元方法求解了二维环境水力学污染源项识别反问题, 主要研究了单点及多点固定污染源项识别问题。纵观研究成果, 这些算法可分为确定性方法和不确定性方法, 其中确定性方法未考虑误差因素, 不确定性方法具有较强的随机性, 收敛速度慢, 计算量随着参数的增多而呈指数增长。
DE算法用于求解连续变量的全局优化问题, 具有种群多样性好、鲁棒性强、隐含并行性、全局寻优能力强等特点[5-6]。与遗传算法[3]相比, DE算法最大的特点是在每一个新个体的生成过程中用到了父代多个个体的线性组合, 而不是遗传算法中传统单一的父代染色体交叉技术。
本研究运用贝叶斯统计方法和二维水质对流-扩散方程, 建立水体污染识别模型, 得到污染源强度、排放位置和排放时刻3个未知参数的后验概率密度函数。运用最大似然估计的思想, 采用微分进化算法, 求解使后验概率密度函数达到最大值的参数, 作为参数的估计值, 实现对水体污染源的识别, 以期为突发性水污染事件反问题研究提供借鉴。
1 模型介绍及问题的提出二维水质对流扩散方程[25]可以表述为
| $ \frac{{\partial C}}{{\partial t}} + {u_x}\frac{{\partial C}}{{\partial x}} + {u_y}\frac{{\partial C}}{{\partial y}} = {D_x}\frac{{{\partial ^2}C}}{{\partial {x^2}}} + {D_y}\frac{{{\partial ^2}C}}{{\partial {y^2}}}-KC, $ | (1) |
式中:C为测点(x, y)在t时刻的污染物的质量浓度, mg/L; t为污染物排放后开始预测的时间, min; Dx、Dy分别为纵向、横向的扩散系数, m2/min; ux、uy分别为纵向、横向的河流平均流速, m/min; K为污染物的降解系数, min-1。
对于瞬时点源岸边排放模式, 方程的解析解[9]可表示为
| $ C(x, y, t) = \frac{M}{{2{\rm{ {\rm{\pi }} }}\mathit{h}\sqrt {{D_x}{D_y}} t}}\exp \left[{-\frac{{{{(x-{u_x}t)}^2}}}{{4{D_x}t}}-\frac{{{{(y - {u_y}t)}^2}}}{{4{D_y}t}} - Kt} \right], $ | (2) |
式中:M为污染源的源强, g; h为河流的平均水深, m; x、y分别为预测点距污染源的纵向、横向距离, m。
假定下游某断面污染物浓度的分布已知, 则突发性水污染反问题的研究就是根据这些已知污染物质量浓度分布来确定污染源的强度、泄露位置和排放时刻, 进而依据式(2)对水体中的污染物进行追踪。
2 Bayesian理论和DE算法Bayesian理论的主要思想是利用搜集到的信息对原有的判断进行修正, 从而得到后验概率分布。本研究中未知参数的后验概率密度函数[21-22]
| $ p(\mathit{\boldsymbol{\alpha |d )= }}\lambda \exp \left\{ {- \sum\limits_{i = 1}^n {\frac{{{{[{\mathit{d}_i}-{\mathit{C}_i}(\mathit{x, y, t|}\mathit{\boldsymbol{\alpha }})]}^2}}}{{2{\sigma ^2}}}} } \right\}, $ | (3) |
式中:α=(α1 α2…αm)为模型的未知参数, 未知参数共有m个; d=(d1 d2 … dn)为实测数据, 实测值共有n个; Ci(x, y, t|α)表示相应于参数α的第i个预测值, εi=di-Ci(x, y, t|α)表示测量误差, i=1, 2, …, n, 并且假定测量误差服从均值为0、标准偏差为σ的正态分布N(0, σ2), 且相互独立; λ表示与参数α的选取无关的常数。
在实测数据d固定的条件下, 式(3)是关于参数α的函数, 也把后验概率密度函数p(α|d)称为似然函数。固定实测数据d, 在参数α的可能取值范围Ω内求解使似然函数p(α|d)达到最大的参数
| $ p\mathit{\boldsymbol{\hat \alpha |d = }}\lambda \mathop {\max }\limits_{\alpha \in \mathit{\Omega }} \;\exp \left\{ {- \sum\limits_{i = 1}^n {\frac{{{{[{\mathit{d}_i}-{\mathit{C}_i}(\mathit{x, y, t|}\mathit{\boldsymbol{\alpha }})]}^2}}}{{2{\sigma ^2}}}} } \right\}。$ | (4) |
要求得式(4)的最大值, 只需求得
| $ \begin{array}{l} f(\mathit{\boldsymbol{\alpha }}) = \mathit{f}{\rm{(}}{\alpha _1}\;\;{\alpha _2}\; \cdots \;{\alpha _m}{\rm{) = }}\\ \;\;\sum\limits_{i = 1}^n {\frac{{{{[{\mathit{d}_i}-{\mathit{C}_i}(\mathit{x, y, t|}\mathit{\boldsymbol{\alpha }})]}^2}}}{{2{\sigma ^2}}}}, \end{array} $ | (5) |
式中:(α1 α2 … αm)是m维连续变量, 其取值范围满足Aj≤αj≤Bj, j=1, 2, …, m。
微分进化算法(DE)[6]主要用于实参数优化问题, 在连续空间问题上优于其他进化算法, 实际中应用广泛。本研究运用DE算法求解上述最值问题。DE算法的工作步骤主要包括变异、交叉、选择操作, 具体步骤见文献[5]。
3 实例分析 3.1 实例假设污染排放为岸边瞬时排入河道。建立二维平面河流水质模型, 设坐标中心为污染源泄漏点, 观测点D坐标为(S0, 0), 泄漏量为M, 泄露时间距离首次监测时间为T0, 故待求参数α=(M, S0, T0)。研究河段的已知和待求的水文水质参数如表 1、2所示[21-22]。
| 表 1 研究河流断面水文水质参数 Table 1 Known hydrological and water quality parameters of studied river's cross section |
| 表 2 研究河流断面待求的水文水质参数 Table 2 Unknown hydrological and water quality parameters of studied river's cross section |
设定观测日当天上午10:00为初始监测时刻, 其后每隔30 min测量一次, 直至当天15:00, 利用表 1、2和式(2)可计算得观测点D的污染物质量浓度di, 共11个计算数据, 污染质量浓度实测值如表 3、图 1所示。
| 表 3 监测点D处污染物观测质量浓度序列 Table 3 Sequence values of pollutant concentration at monitoring point D |
|
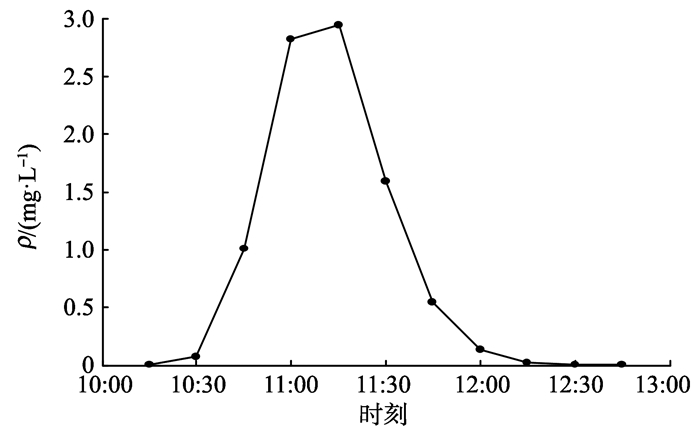
图 1 监测点D处污染物浓度分布 Figure 1 Sequence values of pollutant concentration at monitoring point D |
由图 1可知, D处11组污染物的质量浓度序列近似正态分布, 最高值发生于该日12:00, 污染物质量浓度达到2.945 95 mg/L。
3.2 基于Bayesian-DE方法的模型参数反演结果根据实际问题的先验信息, 可以得到环境水力学模型参数的分布范围, 认为每个参数都服从均匀分布, 且相互独立。本研究依据表 2数据可假设污染源强度M、污染源位置S0和污染源排放时刻T0 3个待求参数的取值范围分别为:0.4×106g≤M≤1.6×106g, 1.0×103m≤S0≤1.0×104m, 50 min≤T0≤200 min。
由式(3)可得待求参数的后验概率密度函数(似然函数):
| $ \mathit{p}{\rm{(}}\mathit{M, }{\mathit{S}_0}{\rm{, }}{\mathit{T}_0}{\rm{|}}\mathit{d}{\rm{) = }}\lambda {\rm{exp}}\left\{ {- \sum\limits_{i = 1}^{11} {\frac{{{{[{d_i}-{C_i}{\rm{(}}\mathit{M, }{\mathit{S}_0}{\rm{, }}{\mathit{T}_0}{\rm{)]}}}^2}}}{{2{\sigma ^2}}}} } \right\}。$ | (6) |
设种群规模NP=100, 变异因子F=0.6, 交叉因子CR=0.9, 按照DE算法迭代280次就可以得到最大似然估计:M=1 Mg, S0=5 km, T0=120 min。
按照Bayesian-DE算法思路迭代200次, 得到模型3个待估参数M, S0, T0的后验概率直方图, 如图 2所示。
|
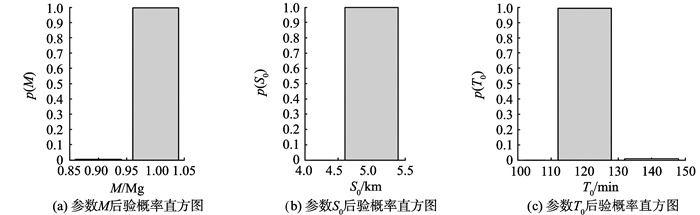
图 2 基于Bayesian-DE方法的模型参数后验概率直方图 Figure 2 Posterior probality histograms of model parameters based on Bayesian-DE |
由图 2可知, 3个模型参数后验概率密度分布呈现不明显的正态分布; 模型的3个待估参数M、S0、T0分别在1 Mg、5 km、120 min附近出现的频度最大, 符合预先设定的真值。
污染源强度M、污染源位置S0和污染源排放时刻T0 3个参数的迭代曲线如图 3所示。
|
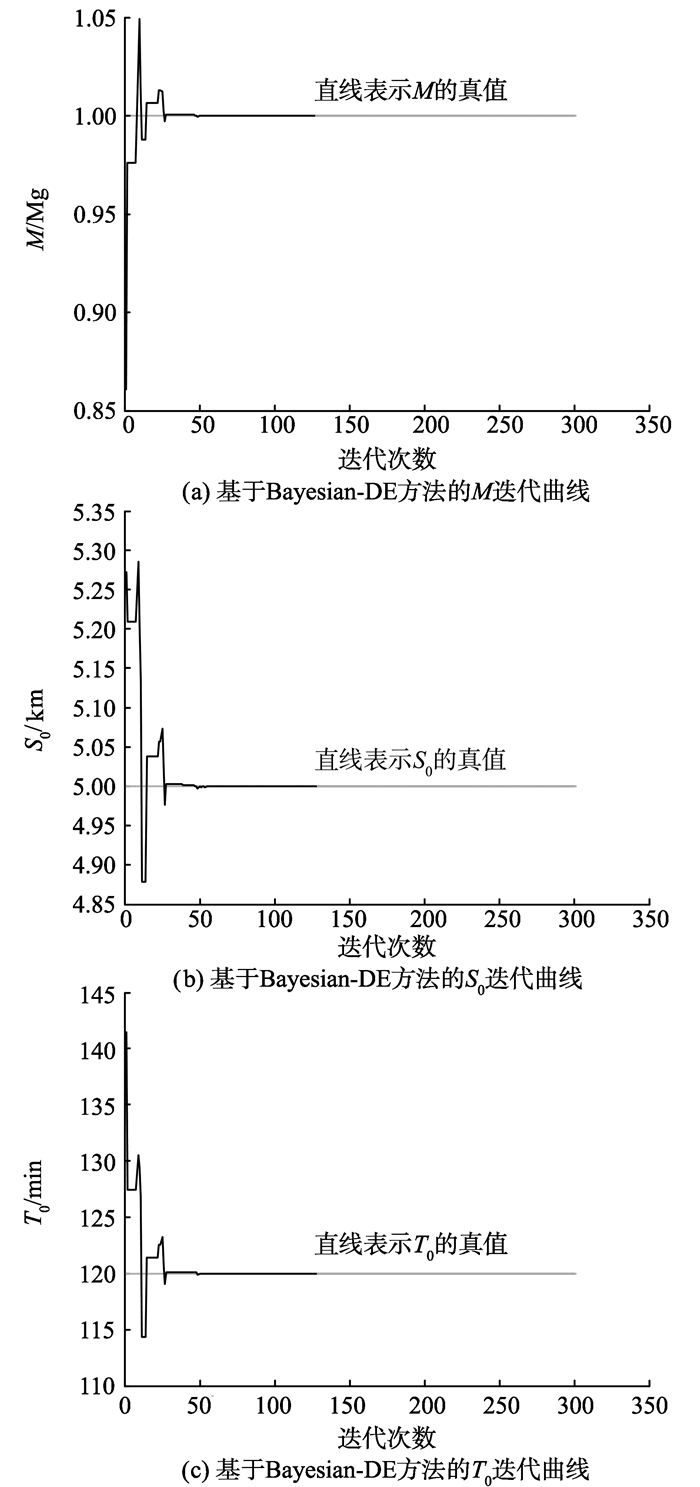
图 3 基于Bayesian-DE方法的模型参数迭代曲线 Figure 3 Iterative curves of model parameters based on Bayesian-DE |
由图 3可知, DE算法迭代到50次时, 3个参数取值基本达到稳定, 并且和真值几乎重合。当迭代次数达到280步时, 3个参数和真值完全重合, 误差此时为0。
3.3 反演效果比较作为比较, 本研究采用Metropolis算法构建马尔科夫链对此模型问题进行求解, 3个待估参数M、S0、T0的迭代曲线如图 4所示。
|
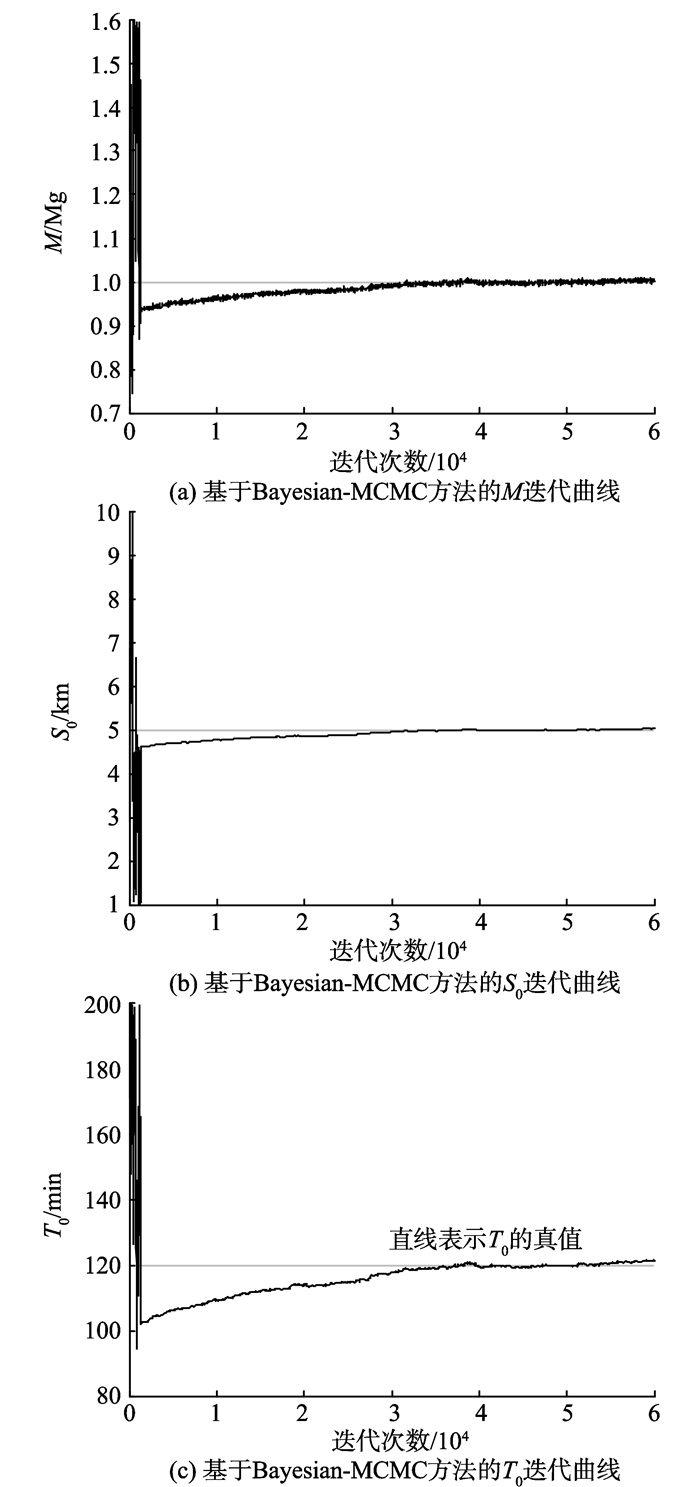
图 4 基于Bayesian-MCMC方法的模型参数迭代曲线 Figure 4 Iterative curves of model parameters based on Bayesian-MCMC |
由图 4可知, Metropolis算法迭代约3 000次后, 3个参数M, S0, T0的马尔科夫链进入稳定收敛域, 直到经过50 000次迭代后, 才能使3个参数的取值和真值近似重合。
为进一步验证Bayesian-DE算法的效果, 对于Bayesian-DE算法迭代结果, 剔除前面50次不稳定结果, 对剩余的150次模型参数进行后验统计分析; 类似, 对于Bayesian-MCMC算法的结果, 剔除前2 000次结果, 对剩余的58 000次模型参数进行后验统计分析, 结果如表 4所示。
| 表 4 Bayesian-DE算法与Bayesian-MCMC算法的模型参数后验统计结果比较 Table 4 Posterior statistical comparison of model parameters between Bayesian-DE and Bayesian-MCMC |
由表 4可知, 采用Bayesian-DE算法所得3个待估参数M、S0、T0的均值误差率分别为11×10-4%、13×10-4%、24×10-4%, 中值误差率分别为12×10-7%、20×10-7%、37×10-7%, 均明显低于Bayesian-MCMC算法的后验统计结果, 说明Bayesian-DE算法估计精度更高。
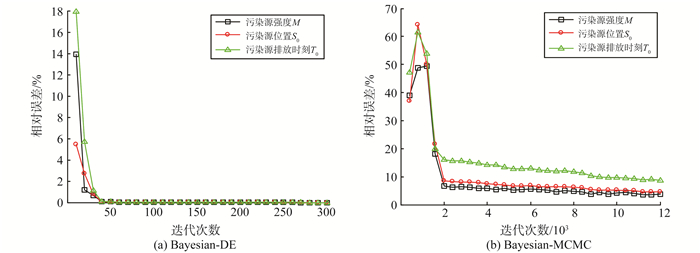
为了比较Bayesian-DE算法与Bayesian-MCMC算法的反演稳定性, 采取多次间隔性提取模型参数误差序列, 结果如图 5所示。
|
图 5 基于Bayesian-DE算法和Bayesian-MCMC算法的反演结果相对误差分析 Figure 5 Relative error analysis of inversion results based on Bayesian-DE and Bayesian-MCMC |
由图 5可知, 采用Bayesian-DE算法迭代约50次后, 可使3个待估参数M、S0、T0反演结果近似于“真值”, 且相对误差控制在1%以内, 而采用Bayesian-MCMC算法迭代约2 000次后, 反演结果才能接近于“真值”, 且相对误差在10%左右。因此, 与Bayesian-MCMC算法相比, Bayesian-DE算法可使3个参数估计值达到稳定时的迭代次数降低97.5%, 且相对误差大幅减小。
4 结论(1) 利用Bayesian-DE方法以概率语言解决突发性水污染事件反问题, 可有效获取污染源信息(污染源强度、污染源位置和污染源排放时刻)。
(2) 算例中, 与Bayesian-MCMC算法相比, Bayesian-DE算法可使污染源信息的3个未知参数估计值达到稳定时的迭代次数降低97.5%, 均值误差分别减少1.69%、2.12%和4.03%。在参数反演识别方面, Bayesian-MCMC算法具有收敛快、精度高的特点, 其可靠性和稳定性均高于Bayesian-MCMC算法。
| [1] | WEI H, CHEN W, SUN H, et al. A coupled method for inverse source problem of spatial fractional anomalous diffusion equations[J]. Inverse Problems in Science and Engineering, 2010, 18(7): 945-956 DOI:10.1080/17415977.2010.492515 |
| [2] | JHA M, DATTA B. Three-dimensional groundwater contamination source identification using adaptive simulated annealing[J]. Journal of Hydrologic Engineering, 2012, 18(3): 307-317 |
| [3] | HOLLAND J. Adaptation in natural and artificial systems[M]. Ann Arbor: University of Michigan Press, 1975. |
| [4] | RUZEK B, KVASNICKA M. Differential evolution algorithm in the earthquake hypocenter location[J]. Pure and Applied Geophysics, 2001, 158(4): 667-693 DOI:10.1007/PL00001199 |
| [5] |
赵光权. 基于贪婪策略的微分进化算法及其应用研究[D]. 哈尔滨: 哈尔滨工业大学, 2007.
ZHAO Guangquan. Differential evolution algorithm with greedy strategy and its applications[D]. Harbin: Harbin Institute of Technology, 2007. |
| [6] |
苏海军, 杨煜普, 王宇嘉. 微分进化算法的研究综述[J].
系统工程与电子技术, 2008, 30(9): 1793-1797 SU Haijun, YANG Yupu, WANG Yujia. Research on differential evolution algorithm: a survey[J]. Systems Engineering and Electronics, 2008, 30(9): 1793-1797 |
| [7] | STRON R, PRICE K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359 DOI:10.1023/A:1008202821328 |
| [8] | ABBASS H A. The self-adaptive Pareto differential evolution algorithm[C]//Proceedings of 2002 IEEE Congress on Evolutionary Computation. Honolulu, USA: IEEE, 2002: 831-836. |
| [9] | STRON R, PRICE K. Minimizing the real functions of the ICEC'96 contest by differential evolution[C]//IEEE International Conference on Evolutionary Computation. Nagoya, Japan: IEEE, 1996: 842-844. |
| [10] | BECERRA R, COELLO C. Cultured differential evolution for constrained optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(33-36): 4303-4322 DOI:10.1016/j.cma.2005.09.006 |
| [11] | BREST J, GREINER S, BOSKOVIC B, et al. Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems[J]. IEEE Transaction on Evolutionary Computation, 2006, 10(6): 646-657 DOI:10.1109/TEVC.2006.872133 |
| [12] | FAN H, LAMPINEN J. A trigonometric mutation operation to differential evolution[J]. Journal of Global Optimization, 2003, 27(1): 105-129 DOI:10.1023/A:1024653025686 |
| [13] | CHAKRABORY U, DAS S, KONAR A. Differential evolution with local neighborhood[C]//IEEE Congress on Evolutionary Computation. Vancouver, Canada: IEEE, 2006: 2042-2049. |
| [14] |
郝竹林, 冯民权, 闵涛, 等. 地下水渗流参数反演的微分进化算法[J].
自然灾害学报, 2015, 24(1): 55-60 HAO Zhulin, FENG Minquan, MIN Tao, et al. Differential evolution algorithm for parameter inversion of groundwater seepage flow[J]. Journal of Natural Disasters, 2015, 24(1): 55-60 |
| [15] |
刘英霞, 王希常, 唐晓丽, 等. 基于小波域特征和贝叶斯估计的目标检测算法[J].
山东大学学报(工学版), 2017, 47(2): 63-70 LIU Yingxia, WANG Xichang, TANG Xiaoli, et al. Object detection algorithm based on Bayesian probability estimation in wavelet domain[J]. Journal of Shandong University(Engineering Sciences), 2017, 47(2): 63-70 |
| [16] | HAARIO H, SAKSMAN E, TAMMINEN J. An adaptive metropolis algorithm[J]. Bernoulli, 2001, 7(2): 223-242 DOI:10.2307/3318737 |
| [17] | ZENG L, SHI L, ZHANG D, et al. A sparse grid based Bayesian method for contaminant source identification[J]. Advances in Water Resources, 2012, 37(1): 1-9 |
| [18] |
王海军, 葛红娟, 张圣燕. 基于L1范数和最小软阈值均方的目标跟踪算法[J].
山东大学学报(工学版), 2016, 46(3): 14-22 WANG Haijun, GE Hongjuan, ZHANG Shengyan. Object tracking via L1 norm and least soft-threshold square[J]. Journal of Shandong University(Engineering Sciences), 2016, 46(3): 14-22 |
| [19] |
曹瑛, 王明文, 陶亮. 基于Markov网络的检索模型[J].
山东大学学报(理学版), 2006, 41(3): 126-130 CAO Ying, WANG Mingwen, TAO Liang. Information retrieval model based on Markov network[J]. Journal of Shandong University(Natural Science), 2006, 41(3): 126-130 |
| [20] |
曾平, 王婷. 贝叶斯错误发现率[J].
山东大学学报(医学版), 2012, 50(3): 120-124 ZENG Ping, WANG Ting. Bayesian false discovery rate[J]. Journal of Shandong University (Health Sciences), 2012, 50(3): 120-124 |
| [21] |
陈海洋, 腾彦果, 王金生, 等. 基于Bayesian-MCMC方法的水体污染识别反问题[J].
湖南大学学报(自然科学版), 2012, 39(6): 74-78 CHEN Haiyang, TENG Yanguo, WANG Jinsheng, et al. Event source identification of water pollution based on Bayesian-MCMC[J]. Journal of Hunan University(Natural Sciences), 2012, 39(6): 74-78 |
| [22] |
杨海东, 肖宜, 王卓民, 等. 突发性水污染事件溯源方法[J].
水科学进展, 2014, 25(1): 122-128 YANG Haidong, XIAO Yi, WANG Zhuomin, et al. On source identification method for sudden water pollution accidents[J]. Advances in Water Science, 2014, 25(1): 122-128 |
| [23] |
闵涛, 周孝德, 张世梅, 等. 对流-扩散方程源项识别反问题的遗传算法[J].
水动力学研究与进展, A辑, 2004, 19(4): 520-524 MIN Tao, ZHOU Xiaode, ZHANG Shimei, et al. Genetic algorithm to an inverse problem of source term identification for convection-diffusion equation[J]. Journal of Hydrodynamics(Ser.A), 2004, 19(4): 520-524 |
| [24] |
牟行洋. 基于微分进化算法的污染物源项识别反问题研究[J].
水动力学研究与进展(A辑), 2011, 26(1): 24-30 MOU Xingyang. Research on inverse problem of pollution source term identification based on differential evolution algorithm[J]. Journal of Hydrodynamics(Ser.A), 2011, 26(1): 24-30 |
| [25] | 郑春苗, BENNETTG D. 地下水污染物迁移模拟(第二版)[M]. 北京: 高等教育出版社, 2009: 70-79. |




