2. 山东大学电气工程学院, 山东 济南 250061;
3. 山东大学(威海)机电与信息工程学院, 山东 威海 264209
2. School of Electrical Engineering, Shandong University, Jinan 250061, Shandong, China;
3. School of Mechanical Electrical & Information Engineering, Shandong University, Weihai 264209, Shandong, China
为应对能源与环境问题, 我国已向世界发出了发展全球能源互联网的倡议[1], 特高压输电、可再生能源发电等大量电力工程亟待建设, 因此电力建设项目管理将面临巨大的挑战。在管理电力工程建设项目施工, 特别是制定项目进度计划时, 如果未根据实际情况考虑工期与成本的关系以及多资源的分配等对活动工期带来的影响, 或者施工过程中某一施工活动受到意外因素的影响, 则会发生工期偏移[2], 当调控不当时, 必然造成整体项目逾期、抬高造价等问题。因此, 采用先进的工程进度管理手段, 提高工期优化水平, 有助于保障大型工程项目的顺利施工, 创造更高的社会价值。
由GOLDRATT E M[3]提出的关键链法(critical chain method, CCM)已历经近20 a的发展完善, 在电力工程建设项目进度优化管理中有着广泛的应用[4-6]。但在应用中也发现, 关键链法仍存在不足, 集中表现在资源约束处理不合理及按50%完工概率估算工期过于保守两方面。文献[7]指出, 关键链法应用于项目进度优化充分体现了系统工程的管理思想, 但在资源约束和不确定性因素的处理上需改进。由于资源受限的项目进度优化是著名的非确定性问题, 因此如何处理资源约束尤为重要。研究者也在考虑资源约束的情况下不断对关键链法进行改进。文献[8]提出了一种改进的关键链法项目进度优化算法, 以极小化项目周期和极小化库存为优化目标, 将对资源的约束转化为考虑资源限制自由工作时间区间, 采用启发式方法求解, 但当资源发生冲突时, 该研究方法不能适用。而对资源冲突的问题, 文献[9]仍是基于CCM的缓冲区思想, 提出在相邻两活动间设置缓冲区, 缓冲区大小则是根据资源约束的松紧情况和工程的风险偏好等因素通过模糊Delphi算法估计, 研究内容启发了对缓冲区应用的方式, 合理根据资源情况确定和使用缓冲区、不再局限于仅将缓冲区设定在末了活动节点上, 不足在于只考虑资源对单个活动的影响, 而非整个项目; 文献[10]的缓冲区确定则基于活动工期的概率分布, 整体考虑了关键链上的活动影响, 但仍缺乏完整的各活动进度安排。对于关键链法的进度安排, 文献[11]分析指出, GOLDRATT E M提出的将50%的剩余活动工期设为缓冲区的做法会导致严重的浪费; 文献[12]基于约束理论(theory of constraint, TOC)进行分析后, 指出按50%完工概率制定工期计划并非适用于所有活动, 进而给出了一种由活动的重要性和难易程度决定修正系数并以其修正完工概率的方法。但修正系数的计算仍较多地依赖主观因素。
针对上述问题, 本研究分析提出了一种基于完工概率修正的关键链法项目进度优化方法, 在根据项目活动施工情况完善工期-成本表达的基础上建立进度优化模型并提出相应的求解算法。在模型建立中, 以关键度表现资源对活动的约束程度并以此修正完工概率, 再转化为工期约束的形式加入模型, 同时仍保留缓冲区作为可变工期约束。在优化求解中, 通过维持关键链不变, 实现进度计划按优化结果重新分配调整。针对资源变动或进度偏离的情况, 本研究方法也可实现对关键链或缓冲区做出调整, 经再优化形成新的进度计划。最后用某变电站建设算例对方法的可行性和有效性进行了验证。
1 关键链法及存在的问题 1.1 关键链法简述关键链法是约束理论在项目管理中的应用成果[13]。针对工期不确定性, 其基本思想是, 根据概率理论和组织行为学理论确定50%完工概率, 以此对工期进行估计并设定进度计划, 将业主的期望工期与工期估计值的差值按一定原则设置为项目缓冲区, 并进一步确定项目进度计划。
(1) 制定施工网络图
按50%完工概率预估各个活动的工期及确定关键路径、关键工序。
(2) 确定关键链、设置缓冲区
对有资源冲突的活动, 按设定原则(如关键工序优先、自由时间少优先)排序, 顺序使用该资源; 根据活动重新排列造成的逻辑关系改变调整进度计划, 并以改变后计划的最长路径作为关键链; 将剩余50%的时间作为缓冲区, 按一定比例分配在不同节点位置(如关键链与非关键链的接驳点处或关键链最后)。
(3) 关键链及进度计划的动态调整
随着施工的进行, 不断找出制约关键链上活动的各类约束, 再集中资源或调整工期以消除约束的限制。这一过程会导致进度变化, 因此需重新确认关键链及制定进度计划, 优化可循环往复进行直至项目施工完成。
对施工中可能产生的资源约束, 关键链法的处理思想本质上是将其产生的工期不确定性通过缓冲区的再分配加以消除。这种做法有利于调动施工人员的积极性, 还可在出现偏差或不确定因素影响时, 利用缓冲区的作用将工期控制在要求范围内。
1.2 存在的问题项目优化管理的三大目标分别是成本、进度和质量, 三者互相制约, 有着不可分割的联系。目前采用的关键链法项目进度优化方法, 都未考虑不同项目活动受资源约束的差异, 往往存在资源约束的处理与关键链结合不足的问题, 这实质上是由于未能在进度优化中正确反映资源与成本、进度或质量之间的关系造成的。
另外, 一律以50%完工概率对项目活动的工期进行估计, 虽为后续调整留出了充足的缓冲区, 但这种对工期的极限压缩必然导致过于频繁的调整, 应用于大型工程项目管理中势必造成调整工作量过大。
因此, 关键链法项目进度优化方法有待在上述方面进行改进。
2 资源约束的新处理资源约束下的项目进度优化, 核心是解决项目施工中的资源配置问题, 衡量资源约束对项目活动的影响, 重在处理工期和资源之间的关系。
一般来说, 项目活动受资源约束的程度可用关键度[14]表示, 其数学表达式为
| $ \rho (i) = \frac{n}{{m + 1}}, $ | (1) |
式中: ρ(i)为关键度;ρ(i)∈[0, 1); m为资源约束总数; n为不同资源约束下第i个活动在关键路径中出现的累积次数。
关键链法设定各个活动的工期时, 一般按照最低完工概率Plow, 通常设为50%进行预估, 即Plow=0.5。在Plow对应的工期下, 分别考虑各资源约束, 因为不同资源约束引起冲突的情况不同, 活动的排序会有差别, 所以不同资源约束下得到的关键链也是不同的。
对项目的某一活动而言, 当其关键度越大, 证明其所受资源约束程度越高, 在整个项目中越关键, 且关键工序工期一般较长, 自由时间较少。而当提高最低完工概率时, 活动的预估工期随即增大, 由此可见关键度大的活动适用更高的最低完工概率。
此处假设, 当关键度取最大值
综上, 本研究提出一种工期-资源间关系的新型处理方式, 即将项目活动的完工概率和关键度相结合, 建立数学表达式
| $ {\mathit{P}_{{\rm{low}}}}(i)' = \rho (\mathit{i}{\rm{)[}}{\mathit{P}_{{\rm{up}}}}{\rm{(}}\mathit{i}{\rm{)-}}{\mathit{P}_{{\rm{low}}}}(\mathit{i}{\rm{)] + }}{\mathit{P}_{{\rm{low}}}}(\mathit{i}{\rm{), }} $ | (2) |
则资源约束变为完工概率的约束
| $ {\mathit{P}_{{\rm{low}}}}(i)' \le \rho (\mathit{i}{\rm{)}} \le {\mathit{P}_{{\rm{up}}}}{\rm{(}}\mathit{i}{\rm{)}}。$ | (3) |
当确定了项目活动的关键度, 就可由式(2)(3)得到活动i的工期ti在资源约束下最低完工概率的适用值, 进而预估形成对工期的约束
| $ {{t'}_{i{\rm{low}}}} \le {t_i} \le {t_{i{\rm{up}}}}, $ | (4) |
式中:t′ilow表示完工概率P′low(i)下项目活动i的工期预估值, tiup表示完工概率Pup下工期的预估值。
这种资源约束处理方式充分说明:关键度越高的活动对完工概率要求也就越高, 受资源约束程度越大的活动对工期的要求越长, 很符合工程实际。同时, 也兼顾到在处理牵涉较多资源的关键活动时, 工期要适当压缩, 不能过度。
3 本研究方法 3.1 进度优化模型进度优化管理中考虑资源约束的意义在于, 资源最直接地体现了成本, 控制资源的使用、按资源合理分配制定进度计划, 本质上是成本控制[15]。据此分析可知, 一般投入的资源越多, 成本越大, 项目完成的工期会越短; 反之, 投入的资源越少, 成本越小, 项目完成的工期会越长。一定的资源投入对应一定的项目完成工期。因此工期-成本模型是项目进度优化的重要依据, 正确建立工期-成本关系是确保进度优化的关键一环。工程项目的成本一般由直接成本与间接成本组成, 直接成本和工期近似成反比, 间接成本和工期近似成正比[16], 并且工期-成本关系可分为线性与非线性、凹凸关系、连续与离散等各类不同的表达[17]。现有的工期-成本模型大多未考虑工程不同阶段成本组成的变化[18], 并且在实际应用中普遍采取工期-成本的线性化表达, 这显然是不合理的, 工期-成本关系的表达有待完善。一般工程的直接成本占工程总成本的80%左右, 如果能把直接成本控制好, 那么项目的总成本控制也就成功了70%以上[19]; 而间接成本的概算随施工活动划分情况而变, 许多的间接成本要在划分出的活动间分摊, 概算量大且难以做到准确预估, 但活动一旦进入施工就能够较清楚、准确地获得成本的信息[20]。基于此, 本研究将项目成本分为未施工和已完工/正在施工两类活动考虑, 完善了工期-成本关系的表达。
进度优化的数学模型为
| $ \min AC = \sum\limits_{{\rm{Done/Doing}}} {T{C_i} + } \sum\limits_{{\rm{Unstart}}} {D{C_i}}, $ | (5) |
| $ \begin{array}{l} {\rm{s}}{\rm{.t}}{\rm{.}}\\ \;\;\;\;\;\sum {{x_{{\rm{CRT}}{i}}} - \sum {{x_{{\rm{NOM}}{i}}} \le \sum {{t_{{\rm{CRT}}{i}}} - \sum {{t_{{\rm{NOM}}{i}}},} } } } \end{array} $ | (6) |
| $ 1-{\lambda _i}{x_i} \ge {Q_i}, $ | (7) |
| $ {\mathit{x}_i} \le {t_{i{\rm{up}}}}-{{t'}_{i{\rm{low}}}}, $ | (8) |
| $ \sum\limits_{i = 1}^{{\rm{critic}}} {{x_i} \ge N, } $ | (9) |
| $ {t_i} = {t_{i{\rm{up}}}}-{x_i}, $ | (10) |
式(5)中AC表示在tiup基础上压缩工期带来的项目成本增加量。AC由两部分组成,
式(6)是为了保证进度优化过程中的关键链不变, 即以关键链上的某个节点为起点, 经过有限不重复活动后回到该节点构成的闭合圈上, 压缩关键链上活动的时间和不超过非关键链上活动的总时差。其中tCRTi、xCRTi分别为闭合圈上属于关键链第i个活动在完工概率为Pup下的工期和压缩量; tNOMi、xNOMi分别为闭合圈上非关键链上第i个活动在完工概率为Pup下的工期和基于该工期上的压缩量。
式(7)表示压缩工期时对施工质量Qi的要求, 假设工期与施工质量成正比, 压缩工期则降低施工质量, 其中xi为在tiup基础上压缩的工期, λi为单位压缩工期与施工质量之间的转换系数。
式(8)给出了压缩工期的上限约束, 根据式(4), 其要求为不大于不考虑资源约束时最大完工概率Pup对应工期与考虑资源约束时完工概率P(i)对应工期的差值。
式(9)中N为缓冲区大小, 体现对安全时间集中管理的思想, 将其作为关键链上总的压缩工期下限要求, 可以用于后序的纠偏, 在进度偏离后的优化中可以随实际情况而调整N, 但不能超过初值。
式(10)为ti为考虑资源约束的进度优化结果。
3.2 求解步骤上述模型可采用以下步骤求解:
(1) 绘制项目活动分解及施工网络计划图。将施工项目划分为活动项, 并分别给予编号; 考虑活动紧前紧后逻辑关系, 绘制施工网络计划图。
(2) 预估工期。预估项目各活动在完工概率为Plow=0.5、Pup=1下的工期tilow、tiup。
(3) 计算关键度。以tilow为工期, 分别求不同单资源约束下的关键链, 记录各活动在关键链上出现次数, 按式(1)求解各活动关键度。
(4) 修正完工概率。对项目各活动建立如式(2)(3)的关键度修正的完工概率Plow(i)′, 并按Plow(i)′预估得到项目各活动的工期t′ilow, 再形成如式(4)的工期约束。
(5) 修正关键链。以t′ilow为工期, 求解考虑所有资源约束下的关键链以及与该关键链构成的闭合圈。
(6) 建立项目进度优化模型并求解。按未施工活动、已完工/正在施工的活动, 分别完善其工期-成本表达, 并建立优化模型; 采用GAMS软件进行求解。
(7) 优化进度计划调整。当监测到资源约束发生变动或实际进度偏离计划(偏差大于设定值)时返回步骤(3), 重新进行进度优化; 直至最后一道工序完工, 结束整个项目的进度优化。
4 算例分析以山东省某地220 kV变电站施工数据为例, 利用本研究方法进行项目进度优化。该变电站施工活动可划分为25项活动, 按1~25分别给予编号, 各活动内容及相关数据参数详见表 1。
| 表 1 施工活动内容及相关数据 Table 1 Construction activity data |
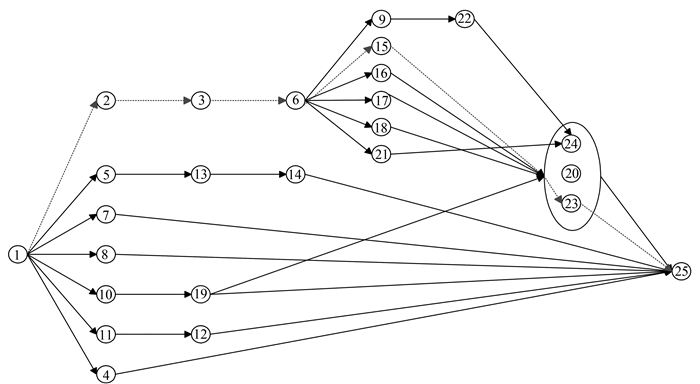
根据表 1, 单代号网络计划图绘制如图 1所示, 点线表示t′ilow下考虑所有资源约束得到的关键链。优化求解分为两部分, 一是项目施工前的初步进度优化, 二是项目施工过程中发生进度偏离后的调整进度优化。
|
图 1 施工网络计划图 Figure 1 Construction network plan |
(1) 初步进度优化
设定缓冲区N=25, 采用三种方法分别求取项目进度优化计划。
方法Ⅰ:保守进度计划制定方法, 即在工期为tiup下确定关键链制定进度计划。
方法Ⅱ:完工概率50%下采用关键链法的进度计划制定方法。
方法Ⅲ:本研究方法, 即关键度修正的完工概率下采用关键链法制定进度计划的方法。
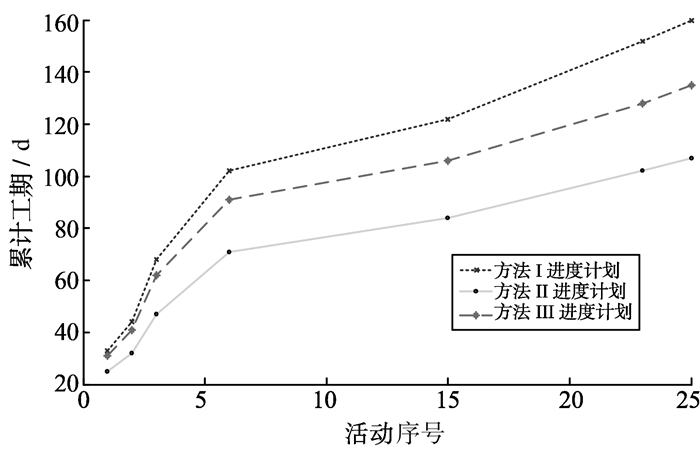
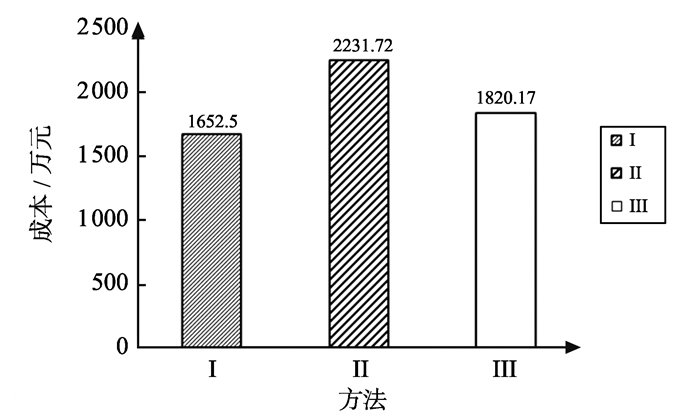
各方法所得计划工期和成本结果如图 2、3所示。由图 3可知, 方法Ⅲ和方法Ⅱ的计划工期相较方法Ⅰ分别缩短了25 d和53 d, 缩短比例分别为15.63%、33.13%, 而成本分别增加167.67万元和579.22万元, 变化比例分别为10.15%与35.05%, 可认为方法Ⅲ在优化工程工期的同时又能控制好成本支出, 有较为明显的优化效果。
|
图 2 初步进度优化工期对比图 Figure 2 Preliminary schedule optimization′s comparison in construction time |
|
图 3 初步进度优化成本对比图 Figure 3 Preliminary schedule optimization′s comparison in construction cost |
进一步分析方法Ⅲ和方法Ⅱ的进度计划, 可见两者都能满足项目的工期控制要求, 但方法Ⅱ的进度计划中需要过分压缩工期, 造成成本升高。实际工程中关键链上的活动相关联的资源数一般较多, 受资源约束明显, 为使各活动尽可能按计划施工, 留给工期压缩的范围一般较小, 过分压缩工期需要更多的人力物力, 所以这种工期的过分压缩虽满足了工期要求但代价更大。
(2) 进度偏离后的调整进度优化
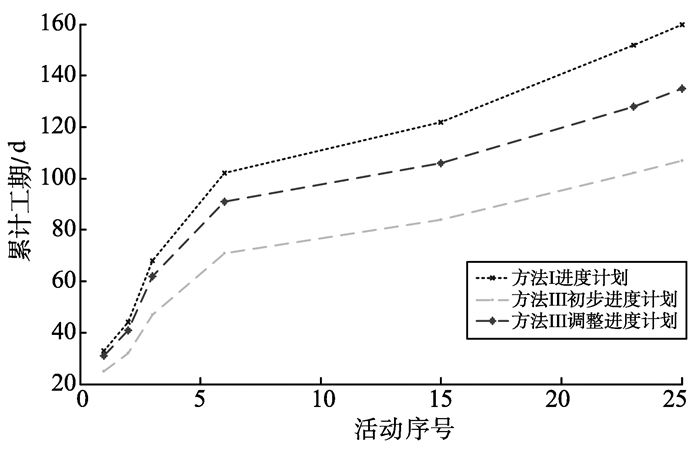
假设施工中监测到活动15有实际进度与计划进度偏差超过设定值的情况发生, 需重新调整计划。经监测, 关键资源数目未发生改变, 重新预估各活动的工期后发现关键链和闭合圈都未改变。于是重构活动15的工期-成本函数, 得到TC15=0.41x152-0.62x15-0.17, 带入优化目标函数, 求解得活动15的工期t′ilow由15变成18, tiup由20变为23。除了活动15外, 监测到已完工的活动6也存在偏差, 由初步优化的进度计划中的28 d变成32 d, 其他活动按照既定计划进行, 其工期-成本关系未改变。将变动后的数据带入模型再进行优化求解, 得到优化结果如图 4、5所示, 图 4、5中也给出方法Ⅰ的结果及方法Ⅲ初步优化结果。
|
图 4 进度偏离后优化工期对比图 Figure 4 Optimization′s comparison in construction time after schedule deviation |
|
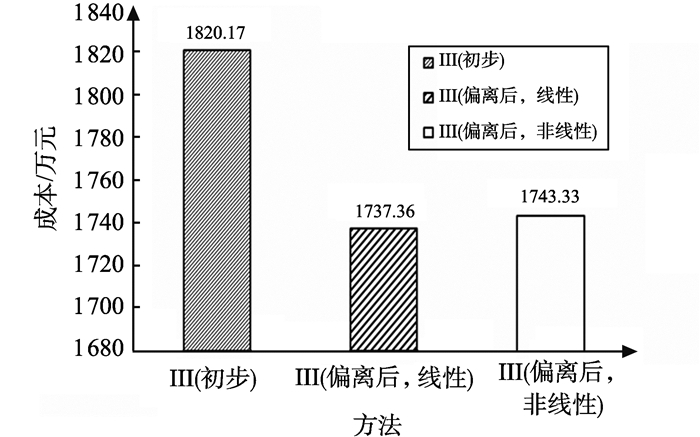
图 5 进度偏离后优化成本对比图 Figure 5 Optimization′s comparison in construction cost after schedule deviation |
由图 4可以看出, 初步优化后的总工期和调整后的总工期曲线最终未交汇于一点, 调整后的总工期较初步优化后的工期小, 这是因为初始的工期缓冲区设为N=25, 但因为活动15及其之前出现了偏离, 判定关键链上已压缩活动工期和剩余可压缩活动工期之和为19, 小于原缓冲区值, 此时需重新调整缓冲区, 令N=16。对单个活动, 除了关键链上活动的工期发生改变, 也有部分非关键路径上活动的工期随之改变, 则是因为闭合圈约束条件的限制。
在成本方面, 由图 5可见, 较初步优化的成本还有所降低, 这要归因于缓冲区N的减小。仔细剖析发生变动的活动15的成本, 如果不对活动15按施工中活动工期-成本关系调整而按照原线性关系, 则计算成本相较方法Ⅰ将增加为84.86万元, 但按调整后的非线性关系则成本增加为90.83万元。由于活动15相较初步进度计划有一定的延期, 成本支出提高是必然的, 因此本研究方法区分活动是否已施工而采用不同的工期-成本表达是更加符合实际情况的。
5 结语本研究提出了一种新的项目进度优化方法, 通过关键度和完工概率的结合将资源约束以工期形式表达, 在保证完工概率不低于关键链法一致要求的50%的基础上, 进一步根据牵涉的资源数及缓冲区大小修正完工概率, 从而解决了明显受资源约束的活动工期要求过于笼统和过于保守的问题; 根据是否可准确获取成本信息完善了项目活动的工期-成本关系表达, 精确了进度优化的依据。算例分析表明, 本研究的进度优化模型及求解方法是有效的, 并且在资源变化及进度偏离等情况下同样可灵活地实现进度优化。本研究方法有助于提高大型施工项目的进度优化及调整控制水平, 具有良好的应用前景。
| [1] | 刘振亚. 全球能源互联网[M]. 北京: 中国电力出版社, 2015. |
| [2] | ATTALLA M, HEGAZY T, MCKIN R. Project performance control in reconstruction projects[J]. Journal of Construction Engineering and Management, 2000, 126(2): 137-141 DOI:10.1061/(ASCE)0733-9364(2000)126:2(137) |
| [3] | GOLDRATT E M. Critical chain[M]. New York: The North River Press, 1997. |
| [4] |
王倩. 输变电工程项目进度管理—基于关键链理论[J].
工程经济, 2015, 25(5): 46-52 WANG Qian. Project schedule management of power transmission and transformation project—based on the critical chain theory[J]. Engineering Economy, 2015, 25(5): 46-52 |
| [5] |
周杰. 基于关键链方法的智能变电站建设项目进度管理研究[D]. 北京: 华北电力大学, 2014.
ZHOU Jie. Research on schedule management of intelligent substation construction project based on the critical chain method[D]. Beijing: North China Electric Power University, 2014. |
| [6] |
张斌. 基于模糊关键链法的工程进度管理研究—以开张35 kV变电站增容改造项目为例[J].
中国电力教育, 2012(18): 117-126 ZHANG Bin. Research on project schedule management based on fuzzy critical chain method—A case study of capacity renovation project of 35 kV substation in Kaizhang city[J]. China Electric Power Education, 2012(18): 117-126 |
| [7] |
金敏力. 基于关键链的项目优化调度问题研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.
JIN Minli. Research on the project optimization scheduling based on critical chain[D]. Harbin: Harbin Technical University, 2013. |
| [8] |
刘士新, 宋健海, 唐加福. 基于关键链的资源受限项目调度新方法[J].
自动化学报, 2006, 32(1): 60-66 LIU Shixin, SONG Jianhai, TANG Jiafu. Critical chain based approach for resource-constrained project scheduling[J]. Acta Automatica Sinica, 2006, 32(1): 60-66 |
| [9] | GUO Y, DONG C. Resource conflict resolution method for software projects using fuzzy critical chain[C]// Control and Decision Conference. Changsha, China: IEEE, 2014: 2554-2559. |
| [10] | YU J, XU Z, HU C. Buffer sizing approach in critical chain project management under multiresource constraints[C]// International Conference on Information Management, Innovation Management and Industrial Engineering. Xi'an, China: IEEE, 2014: 71-75. |
| [11] | ASHTIANI B, JALALI G R, ARYANEZHAD M B, et al. A new approach for buffer sizing in critical chain scheduling[C]// IEEE International Conference on Industrial Engineering and Engineering Management. Singapore, Singapore: IEEE, 2007: 1037-1041. |
| [12] | WEI C C, LIU P H, TSAI Y C. Resource-constrained project management using enhanced theory of constraint[J]. International Journal of Project Management, 2002, 20(7): 561-567 DOI:10.1016/S0263-7863(01)00063-1 |
| [13] |
李恩成. 基于关键链技术的工程建筑项目进度管理方法研究[D]. 北京: 华北电力大学, 2015.
LI Encheng. Based on critical chain engineering construction project management method research[D]. Beijing: North China Electric Power University, 2015. |
| [14] |
王仁超, 欧阳斌, 王琳, 等. 工程项目计划"关键性"问题拓展研究[J].
系统工程与电子技术, 2004, 26(7): 914-917 WANG Renchao, OUYANG Bin, WANG Lin, et al. Expanded study on criticality in the project network planning[J]. Systems Engineering and Electronics, 2004, 26(7): 914-917 |
| [15] | TERRY S B, LUCKO G. Algorithm for time-cost tradeoff analysis in construction projects by aggregating activity-level singularity functions[C]//Construction Research Congress 2012: Construction Challenges in a Flat World, Proceedings of the 2012 Construction Research Congress West Lafayette, USA: [s. n. ]. 2012: 226-235. |
| [16] |
郭云. 工程项目进度—费用优化研究[D]. 赣州: 江西理工大学, 2014.
GUO Yun. Research progress of optimal control[D]. Ganzhou: Jiangxi University of Science and Technology, 2014. |
| [17] | KELLEY Jr J E. Critical-path planning and scheduling: mathematical basis[J]. Operations Research, 1961, 9(3): 296-320 DOI:10.1287/opre.9.3.296 |
| [18] |
刘英杰. 大型水利工程费用进度集成控制研究[J].
天津大学, 2012 LIU Yingjie. Research on cost and schedule control integration of large-scale water conservancy project[J]. Tianjin University, 2012 |
| [19] |
刘雪峰, 马良超, 姜忠玉. 工程项目成本的预测与控制[J].
四川水力发电, 2007, 26(1): 57-60 LIU Xuefeng, MA Liangchao, JIANG Zhongyu. Prediction and control of project cost[J]. Sichuan Water Power, 2007, 26(1): 57-60 |
| [20] |
赵超. 施工企业工程项目成本核算之探讨[J].
重庆交通学院学报(自然科学版), 2007, 26(1): 130-132 ZHAO Chao. The discussion of business accounting of project cost in construction corporation[J]. Journal of Chongqing Jiaotong University, 2007, 26(1): 130-132 |




