机器人从较高处坠落过程中的冲击会对其机械结构和驱动装置造成极大的损害, 会限制机器人在非结构环境下的机动性和生存能力。腿足式机器人的腿部结构可为躯干提供一定的缓冲距离, 从而保护机器人的核心部件。在相关领域的研究中, 腿部结构等效为刚度与阻尼可变的弹簧[1], 并以此建立模型来研究其缓冲效果。变刚度(阻尼)控制在机器人需要与外部环境相互作用时, 可以减小二者之间的冲击, 使机器人的运动更加柔顺, 还可以提高人机共存环境中的使用安全性[2-5]。1986年, RAIBERT Marc H等人提出弹簧负载倒立摆(spring-loaded inverse pendulum, SLIP)模型和跳跃的3段式控制方式[6-7], 首次在物理平台上对机器人的落地问题进行独立的研究和验证。MORITA Yuichi等人在机器人的控制器中添加独立的碰撞缓冲环节用于减小机器人落地过程中的冲击[8]。SASAHARA Kenta等人通过对关节分别采用位置控制和力控制的方式[9], 使关节既具有位置控制的精确性, 又兼备力控制的柔顺性。陈殿生等人提出, 在机器人落地过程中, 可以通过调整腿部姿态来间接调整躯干在落地过程中的姿态[10], 并提出一套可应用于六足腿式机器人在不同环境下落地的腿部姿态控制方式。HASHIMOTO Kenji等人通过足端速度规划以及减小摆动腿刚度的方法[11], 可减小机器人在崎岖路面上行走所产生的冲击力。KIM Yongduk等人通过在机器人的脚与地面之间添加虚拟被动缓冲装置来减小双足机器人的足端与地面之间的冲击[12]。CHOI Wooseok等人通过研究机器人躯干惯量以及关节处阻尼和刚度对冲击的影响[13], 并基于非线性碰撞模型提出一套可用于多自由度双足机器人的缓冲策略。浦项科技大学研制的一款由串联机构构成的腿型机器人PBot可以从0.50 m的高度自由落下, 并平稳落地[14]。HUTTER Marco等人研发的小型四足机器人StarLETH通过使用串联弹性驱动器(series elastic actuators, SEA)满足落地过程中的柔顺性要求[15-16]。在以上研究中, 机器人的运动过程包含跳跃阶段和落地缓冲阶段。对于跳跃机器人, 其在起跳阶段时, 机器人可以通过调整离地时双腿的力分配方式来稳定躯干的姿态。对于PBot, 由于其无需考虑躯干姿态, 且落地高度相对较低, 控制方式相对简单。
在先前的研究中[17], 通过对四足机器人各关节采用基于比例微分控制的力控制方式(PD力控制), 使其在落地过程中达到良好的缓冲效果。然而, PD参数的整定复杂而繁琐。尤其针对机器人与地面的激烈交互行为, 不仅需要大量的试探, 且难以选择PD参数的最优值。虚拟模型控制无需进行逆运动学的计算[18], 在腿足式机器人的运动控制中具有明显的优势。张国腾等人利用虚拟模型控制验证其在四足机器人步态控制中的可行性[19-20]。本研究利用虚拟模型对机器人的腿部结构进行运动学建模, 通过规划各落地阶段躯干的纵向加速度大小, 计算出各阶段躯干所需要的虚拟合外力, 从而得出腿部各关节所需要的力矩。
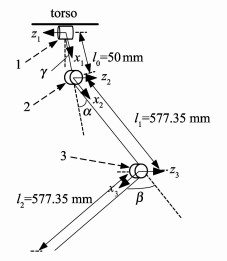
1 模型建立图 1为机器人的结构示意图。机器人的躯干可看作刚体, 腿部膝关节位于刚体质心处。每条腿具有3个旋转关节, 在图中分别用1、2、3表示, 每个关节的关节坐标系和腿部各连杆的主要参数在图中标出。其中, {Ob}为躯干坐标系的原点, 腿部关节坐标系中各坐标系的z轴均为相应关节的旋转轴, 方向见图 1, 关节的旋转方向符合右手定则, 关节坐标系的x轴落在腿部的连杆上, 方向指向下一级关节, 关节坐标系的y轴由坐标系右手定则确定。机器人髋关节1为横滚关节, 髋关节2和膝关节3均为俯仰关节。模型的主要参数均已在图 1中标出。其中, α、β、γ分别为关节2、关节3和关节1的关节角, 且当机器人处于正常站立姿态时, α0=π/6, β0=-π/3, γ0=0。躯干与腿部各连杆均视为刚体, 各部分质心均位于其几何中心处, 横滚髋关节(图 1中关节1)到足端的直线长度定义为机器人腿部的等效长度。
|
图 1 机器人腿部结构图 Figure 1 Leg structure of the robot |
在机器人的躯干坐标系中, 足端坐标(x, y, z)可分别表示为
| $ \left\{ \begin{array}{l} x = {l_2}{s_{\alpha + \beta }} + {l_1}{s_\alpha }, \\ y =-{l_2}{c_{\alpha + \beta }}{c_\gamma }-{l_1}{c_\alpha }{c_\gamma }-{l_3}{c_\gamma }, \\ z = - {l_2}{c_{\alpha + \beta }}{s_\gamma } - {l_1}{c_\alpha }{s_\gamma } - {l_3}{s_\gamma }, \end{array} \right. $ | (1) |
其中, sα+β=sin (α+β), cα+β=cos (α+β), sα=sin α, cγ=cos γ。
对式(1)的两边求微分, 整理得
| $ \left[\begin{array}{l} {\dot x}\\ {\dot y}\\ {\dot z} \end{array} \right] = \left[\begin{array}{l} {\dot \alpha }\\ {\dot \beta }\\ {\dot \gamma } \end{array} \right], $ | (2) |
其中, J为相应的雅可比矩阵, 且
| $ \boldsymbol{J} = \left[{\begin{array}{*{20}{c}} {{l_2}{c_{\alpha + \beta }} + {l_1}{c_\alpha }}&{{l_2}{c_{\alpha + \beta }}}&0\\ {{l_2}{s_{\alpha + \beta }}{c_\gamma } + {l_1}{s_\alpha }{c_\gamma }}&{{l_2}{s_{\alpha + \beta }}{c_\gamma }}&{{l_2}{c_{\alpha + \beta }}{s_\gamma } + {l_1}{c_\alpha }{s_\gamma } + {l_3}{s_\gamma }}\\ {{l_2}{s_{\alpha + \beta }}{s_\gamma } + {l_1}{s_{\alpha + \beta }}{s_\gamma }}&{{l_2}{s_{\alpha + \beta }}{s_\gamma }}&{-{l_2}{c_{\alpha + \beta }}{c_\gamma }-{l_1}{c_\alpha }{c_\gamma }-{l_3}{c_\gamma }} \end{array}} \right]。 $ |
假设地面对足端产生的虚拟力为f=[fx, fy, fz]T, 由作用力与反作用力之间的关系, 则腿部各关节的输出扭矩τ=[τx, τy, τz]T为
| $ \mathit{\boldsymbol{\tau }} = - {\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{f}}。 $ | (3) |
由雅可比矩阵J可知, 在大多数情况下, J是满秩的, 因此机器人足端3个方向上的输出力均为可控的。
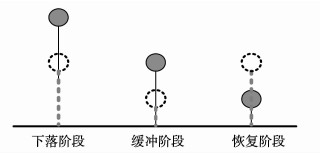
2 过程分析与控制方法整个落地过程可分为3个阶段:下落阶段、缓冲阶段、恢复阶段(见图 2), 此顺序是不可逆的。
|
图 2 落地过程中的3个阶段 Figure 2 Three phases in the whole process |
假设机器人腿部的触地状态为touch, 当touch=1时, 说明腿与地面发生接触; 当touch=0说明腿未与地面发生接触。躯干质心在参考坐标系中的速度为v=[vb, x, vb, y, vb, z], 则3个阶段可概括为下落阶段touch=0, 缓冲阶段touch=1 & vb, y < 0, 恢复阶段touch=1 & vb, y≥0。
对于此机器人而言, 其躯干质量远大于其腿部质量(约为1 000:1), 为简单起见, 腿部质量可以忽略, 即机器人腿部运动不会影响其躯干的姿态。
2.1 下落阶段下落阶段是指机器人由开始下落直至腿部与地面接触, 此阶段的目的是确保机器人在接下来的落地过程中获得最大的缓冲距离, 从而得到最佳的缓冲效果。由于机器人的腿部动作不会影响到躯干的运动状态, 因此, 此阶段只关注腿部姿态即可。当机器人自由下落时, 为得到最大的缓冲距离, 腿部方向应指向躯干的瞬时速度方向(即竖直向下), 其长度维持自然长度。当腿未接触地面时, 其控制采用在足端实际位置与期望位置间添加虚拟“弹簧-阻尼”模型的方式, 该弹簧阻尼系统会拉动相应的摆动腿, 使其跟随期望的足端轨迹运动。
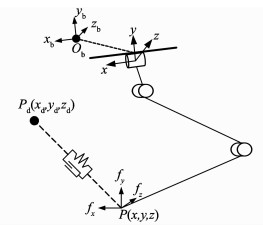
在下落阶段中, 机器人不与外界发生接触, 因此, 机器人在此阶段可看作在空间中是静止的(见图 3)。机器人的躯干质心坐标系如图 3中{Obxbybzb}所示, P为足端在躯干坐标系中的实时位置, 其坐标为(x, y, z), Pd为足端在躯干坐标系中的期望位置, 其坐标为(xd, yd, zd)。参考坐标系原点选在髋关节处, 则相应的足端期望坐标在参考坐标系{O}中可表示为P0=(0, l0, 0), 其中l为腿部在自然状态下的等效长度, m。将P0变化到躯干坐标系中, 得到
|
图 3 下落阶段的虚拟模型 Figure 3 Virtual model in falling phase |
| $ {P_{\rm{b}}}{ = ^{\rm{b}}}{\boldsymbol{T}_0}{P_0} = ({x_{\rm{b}}}, {y_{\rm{b}}}, {z_{\rm{b}}}), $ | (4) |
其中, bT0为由参考坐标系到躯干坐标系变换的变换矩阵。在躯干坐标系中, 足端为达到期望位置所需要的虚拟力f=[fx, fy, fz]可表示为
| $ \left\{ \begin{array}{l} {f_x} = {k_x} \cdot ({x_{\rm{d}}}-x)-{d_x} \cdot \dot x, \\ {f_y} = {k_y} \cdot ({y_{\rm{d}}}-y) - {d_y} \cdot \dot y, \\ {f_z} = {k_z} \cdot ({z_{\rm{d}}} - z) - {d_z} \cdot \dot z, \end{array} \right. $ | (5) |
由式(5)可知, 腿部各关节的关节力矩τ=[τα, τβ, τγ]为
| $ \mathit{\boldsymbol{\tau }} = \left[\begin{array}{l} {\tau _\alpha }\\ {\tau _\beta }\\ {\tau _\gamma } \end{array} \right] = - {\mathit{\boldsymbol{J}}^{\rm{T}}}\left[\begin{array}{l} {f_x}\\ {f_y}\\ {f_z} \end{array} \right]。 $ | (6) |
当机器人的腿与地面接触时, 机器人进入缓冲阶段, 当机器人的躯干质心的位置达到最低点时, 缓冲阶段结束。在此阶段, 为保证缓冲效果, 机器人腿部的虚拟刚度和阻尼是变化的, 机器人的腿部可为躯干提供一个大小恒定虚拟外力并以此为躯干减速, 见图 4。
|
图 4 缓冲阶段的虚拟模型 Figure 4 Virtual model of the buffering phase |
由于腿部质量可以忽略, 则落地过程中的冲击力可根据躯干的质量来规划。
假设在机器人落地瞬间, 腿部的等效长度维持自然长度l0, m, 躯干质心在参考坐标系中的速度为v0, m/s; 在竖直方向上, 地面对足端的支撑力为f, N。则在此过程中, f-mg=ma, 其中:m为躯干质量, kg; a为躯干质心处在竖直方向上的加速度, m/s2。
在缓冲过程中, 机器人躯干质心速度由v0变为0, 此过程的持续时间为tc, s。因此有:v0=at, t为恢复阶段开始至任意时刻的持续时间, s。此外, 机器人所能利用的最大缓冲距离为l0, m, 由此可得l0≥atc/2, 进而可得a≥v02/(2l), 即
| $ {a_{\min }} = v_0^2/(2l)。 $ | (7) |
因此, 从理论上讲, 任意大小满足式(7)的躯干加速度都不会影响到系统的稳定性, 且通常情况下, 为尽量增加缓冲距离, 达到更好的缓冲效果, a应该越小越好。
对于已选定且符合要求的躯干加速度, 由f=ma+mg, 可以得出缓冲阶段地面对足端的支撑力。通过式(3), 可得出腿部各关节所需要的力矩。
2.3 恢复阶段在恢复阶段, 机器人的躯干从最低位置逐渐恢复至正常站立时的高度。在此过程中, 通过加速度规划与PD力控制相结合的方式使机器人达到最终期望的姿态。
恢复阶段可分为两部分:
(1) 从恢复阶段开始直至腿部速度减小为0。此时, 通过对躯干加速度进行规划, 使机器人的躯干达到期望位置。
(2) 恢复阶段剩余的部分。由于单纯的加速度规划会产生位置误差的积累, 此误差可利用PD力控制对其进行补偿, 从而使系统达到稳定的站立状态。
当缓冲阶段开始与结束时, 机器人足端相对于躯干速度均为0, 且在缓冲阶段结束时, 机器人足端相对于躯干的加速度为0。鉴于机器人腿部在缓冲阶段运动的以上特点, 此阶段的躯干纵向加速度采用正弦函数进行规划。加速度
| $ a(t) = m\;\sin (\omega t), $ | (8) |
机器人恢复阶段前半部分的持续时间设定为tc, s, 因此,
| $ a(t) = m\;\sin (\frac{{2{\rm{\pi }}}}{{{t_{\rm{c}}}}}t)。 $ | (9) |
由式(9)可得到躯干在缓冲阶段的纵向速度v(t)和纵向位移s(t), 分别为
| $ v(t) =-\frac{{m{t_{\rm{c}}}}}{{2{\rm{\pi }}}}\cos (\frac{{2{\rm{\pi }}}}{{{t_{\rm{c}}}}}t) + n, $ | (10) |
| $ s(t) =-\frac{{mt_{\rm{c}}^2}}{{2{{\rm{\pi }}^2}}}\cos (\frac{{2{\rm{\pi }}}}{{{t_{\rm{c}}}}}t) + nt + q, $ | (11) |
由初始条件s(0)=l0, s(2)=1, v(0)=0, 其中, 恢复阶段结束时, 腿部长度为1 m。由此可得到式(11)中的未知变量
| $ m = \frac{{1-{l_0}}}{{{t_{\rm{c}}}}}{\rm{\pi }}, n = \frac{{1-{l_0}}}{2}, q = {l_0}, $ | (12) |
即恢复阶段的躯干加速度
在竖直方向上有
| $ f(t)-mg = ma(t), $ | (14) |
得到
| $ f(t) = ma(t) + mg, $ | (15) |
再由式(3)可得到腿部各关节所需要的力矩。
从理论上讲, 机器人会在一个周期内恢复稳定站立的姿态, 然而由于受到位置误差积累的影响作动器响应速度的限制, 当t=tc时, 机器人的躯干速度往往不为0, 这会影响到机器人最终的姿态。因此当t>tc时, 机器人的躯干质心和期望位置之间添加虚拟“弹簧-阻尼”系统, 并依靠此系统将机器人躯干“拖拽”至期望位置, 见图 5。
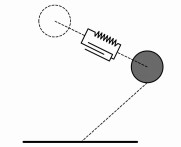
|
图 5 缓冲阶段t>tc时的虚拟模型 Figure 5 Virtual model of the recovering phase (t>tc part) |
此时, 躯干在竖直方向上的虚拟力
| $ {f_y} = {k_y} \cdot \left( {{y_d}-y} \right)-{d_y} \cdot \dot y。 $ | (16) |
再由式(3)可得到腿部各关节处的力矩。
整个落地过程的控制框图见图 6。
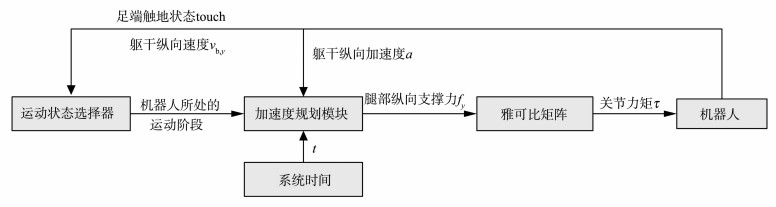
|
图 6 整个过程中的系统控制框图 Figure 6 Control frame of the whole process |
为验证本文中缓冲策略的有效性, 此方法在仿真平台Webots上进行试验。仿真平台中机器人的模型见图 7。
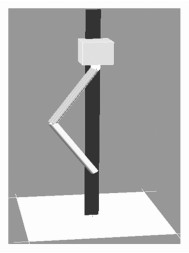
|
图 7 仿真平台中的机器人 Figure 7 The robot in Webots |
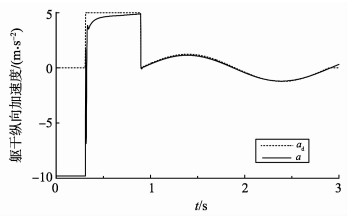
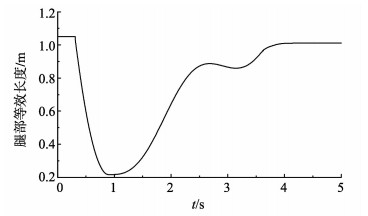
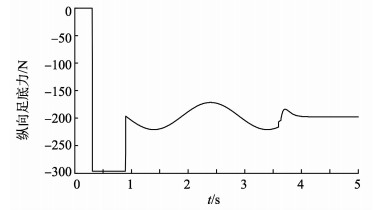
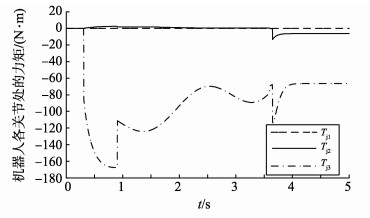
机器人躯干质量为20 kg, 腿部的等效自然长度为1 m。试验过程中, 机器人从躯干质心距离地面1.65 m处自由下落, 观察并记录落地过程中的相关参数。在缓冲阶段, 由计算可知amin=4.89 m/s2, 因此, 取a=5 m/s2。在缓冲阶段第二阶段, 腿部虚拟刚度和阻尼分别为ky=5 000 N/m, dy=1 250 N/(m·s-2)。机器人在试验过程中的录像截图见图 8, 当t=0.32 s时, 机器人进入缓冲阶段, 当t=0.917 s时, 机器人进入恢复阶段。其在落地过程中的相关参数见图 9~12。图 9中, ad和a分别为躯干质心处在竖直方向上的加速度, m/s2。图 12中, Tj1、Tj2、Tj3分别为图 1中标号为1, 2, 3关节处所施加的力矩。由于缓冲阶段持续时间为2 s, 且此试验只对机器人在这一阶段(缓冲阶段2 s内, 总时间2.97 s)的躯干加速度进行规划, 因此, 图 9只将缓冲阶段2 s以前的图像展示出来, 从而观察加速度规划的效果。由图 9可以看出, 躯干在落地过程中受到冲击基本跟随预先规划的曲线而变化, 说明加速度规划在减小落地冲击的过程中是可行的。在图 11与图 12中, 由x轴可以看出, 当机器人运动到3~4 s之间时, 由于控制方式的切换, 系统会出现轻微的震荡, 这并不会影响到机器人的稳定性和缓冲效果。由图 12可以看出, 对于本试验中质量为20 kg的机器人来说, 下落过程中膝盖的峰值负重与普通人上下台阶时的负重相等[21]。因此, 此缓冲策略是有效的。
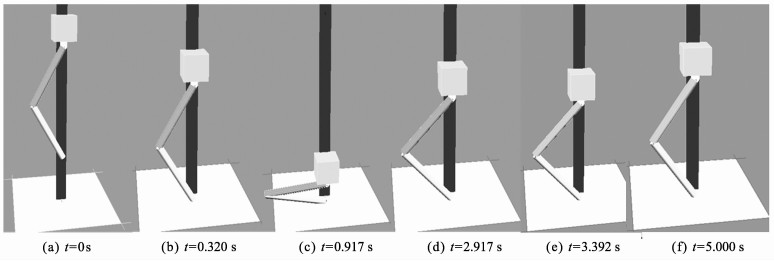
|
图 8 仿真过程的视频截图 Figure 8 Snapshots of the simulation |
|
图 9 躯干质心的纵向加速度 Figure 9 Torso linear acceleration in vertical direction |
|
图 10 机器人的腿部等效长度 Figure 10 Leg length of the leg |
|
图 11 地面对机器人足底的纵向支撑力 Figure 11 Supporting force acting on the foot in vertical direction |
|
图 12 腿部各关节力矩 Figure 12 Torques acting on each joint |
本研究提出一套针对腿足式结构的三段式竖直下落缓冲策略。在缓冲阶段和恢复阶段, 该策略通过对躯干质心纵向加速度的规划, 得到机器人质心所需要的虚拟合外力, 并通过虚拟模型控制, 将此虚拟合外力映射到腿部的各个关节中。该方法具有较强的直观性, 无需复杂的计算。从仿真试验结果看, 此方法对于腿足式机器人的缓冲效果是有效的, 且在缓冲过程中, 躯干的纵向加速度可以跟随期望而变化。因此, 可以根据环境要求, 通过调节期望的加速度变化来直观的调整缓冲的效果, 使PD参数的选择过程得到简化。此外, 尽管算法依然使用PD力控制方式对误差进行补偿, 但此时的躯干运动相对平缓, PD参数易于确定。该方法具有较好的通用性, 可通过合理的力分配方式, 移植到双足、四足或多足机器人上。
在本次仿真试验中, 系统的采样频率较高, 这对于机器人执行器和传感器的处理速度提出很高的要求。将来可通过采用主动柔顺与被动柔顺相结合的方式, 降低算法实现的难度, 使该缓冲策略在物理平台上的得到验证。
| [1] | LIN Abin, ZHOU Jianjun, ZHANG Yaping. Design of joint variable stiffness actuation system of service robot[J]. Journal of Mechanical & Electrical Engineering, 2013, 30 (4) : 439-443 |
| [2] | ZINN Michael, KHATIB Oussama, ROTH Bernard, et al. Playing it safe[J]. IEEE Robotics & Automation Magazine, 2004, 11 (2) : 12-21 |
| [3] | BICCHI Antonio, TONIETTI Giovanni, BAVARO Mi-chele, et al. Variable stiffness actuators for fast and safe motion control[C]//Proceeding of International Symposium on Robotics Research. Berlin, Germany:Springer, 2005:527-536. |
| [4] | ZINN M, ROTH Bernard, KHATIB Oussama, et al. A new actuation approach for human friendly robot design[J]. The International Journal of Robotics Research, 2004, 23 (4) : 379-398 DOI:10.1177/0278364904042193 |
| [5] | VANDERBORGHT Bram, ALBU-SCHÄFFER Alin, BICCHI Antonio, et al. Variable impedance actuators:a review[J]. Robotics and Autonomous Systems, 2013, 61 (12) : 1601-1614 DOI:10.1016/j.robot.2013.06.009 |
| [6] | RAIBERT Marc H, CHEPPONIS Michael, BROWN Benjamin. Running on four legs as though they were one[J]. IEEE Journal of Robotics and Automation, 1986, 2 (2) : 70-82 DOI:10.1109/JRA.1986.1087044 |
| [7] | HODGINS Jessica K, RAIBERT Marc H. Biped gymnastics[J]. The International Journal of Robotics Research, 1990, 9 (2) : 115-128 DOI:10.1177/027836499000900209 |
| [8] | MORITA Yuichi, OHNISHI Kouhei. Attitude control of hopping robot using angular momentum[C]//Proceedings of IEEE International Conference on Industrial Technology. Maribor, Slovenia:The IEEE Press, 2003:173-178. |
| [9] | SASAHARA Kenta, MOTOI Naoki, SHIMONO Tomoyuki, et al. Stable landing method for biped robot by using switching control[C]//Proceeding of IEEE International Workshop on Advanced Motion Control (AMC). Sarajevo, Bosnia and Herzegovina:The IEEE Press, 2012:1-6. |
| [10] | CHEN Diansheng, ZHANG Ziqiang, CHEN Kewen. Legs attitudes determination for bionic locust robot based on landing buffering performance[J]. Mechanism and Machine Theory, 2016, 99 (1) : 117-139 |
| [11] | HASHIMOTO Kenji, HAYASHI Akihiro, SAWATO Terumasa, et al. Terrain-adaptive control to reduce landing impact force for human-carrying biped robot[C]//Proceedings of IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Singapore, Singapore: The IEEE Press, 2009:174-179. |
| [12] | KIM Yongduk, LEE Bumjoo, YU Jeehwan R, et al. Landing force control for humanoid robotby time-domain passivity approach[J]. IEEE Transactions on Robotics, 2007, 20 (6) : 1294-1301 |
| [13] | CHOI Wooseok, DALLALI Houman, MEDRANO-CERDA Gustavo, et al. How leg/foot compliance and posture affects impact forces during landing[C]//Proceedings of IEEE International Conference on Robotics and Biomimetics (ROBIO). Bali, Indonesia:The IEEE Press, 2014:961-967. |
| [14] | SUNG Sanghak, YOUM Youngil. Landing motion control of articulated legged robot[C]//Proceedings of IEEE International Conference on Robotics and Automation. Roma, Italy:The IEEE Press, 2007:3230-3236. |
| [15] | HUTTER Marco, GEHRING Christian, BLOESCH Michael, et al. StarlETH:A compliant quadrupedal robot for fast, efficient, and versatile locomotion[C]//Proceeding of 15th International Conference on Climbing and Walking Robot-CLAWAR 2012. Baltimore, USA: EPFL, 2012:1-8. |
| [16] | PRATT G A, WILLIAMSON M M. Series elastic actuators[C]//Proceeding of IEEE/RSJ International Conference on Intelligent Robots and Systems. Pittsburgh, USA: IEEE, 1995:399-406. |
| [17] | LIU B, CHAI H, RONG X W. A buffering method for quadruped robots based on active impedance control[J]. High Technology Letters, 2016, 4 (1) : 1-8 |
| [18] | PRATT J, DILWORTH P, PRATT G. Virtual model control of a bipedal walking robot[C]//Proceedings of IEEE International Conference on Robotics and Automation. Albuquerque, USA: The IEEE Press, 1997:193-198. |
| [19] |
张国腾, 荣学文, 李贻斌, 等. 基于虚拟模型的四足机器人对角小跑步态控制方法[J].
机器人, 2016, 35 (1) : 64-74 ZHANG Guoteng, RONG Xuewen, LI Yibin, et al. Control of the quadrupedal trotting based on virtual model[J]. Robot, 2016, 35 (1) : 64-74 |
| [20] | ZHANG Guoteng, RONG Xuewen, Chai H, et al. Torso motion control and toe trajectory generation of a trotting quadruped robot based on virtual model control[J]. Advanced Robotics, 2016, 30 (4) : 1-14 |
| [21] |
东九. 了解你的膝盖吗?[J].
驾驶园, 2014, 5 (1) : 52 DONG Jiu. How much do you know about your knees?[J]. World of Driver, 2014, 5 (1) : 52 |




