0 引言

为保证现代化的电力系统安全可靠地运行, 能量管理系统(energy management system, EMS)得到了广泛的应用并发挥了重要作用。电力系统的状态估计是EMS的重要组成部分^[1], 主要功能是利用电力系统的实时冗余量测信息, 对系统状态进行估计, 得到尽可能准确的估计值。状态估计保证了EMS执行不同的控制和决策任务, 例如最优化功率流、电压的稳定性分析、异常数据的检测和分析等^[2-3]。

随着电力系统的飞速发展, 电力系统状态估计, 尤其是动态状态估计, 受到了不同领域学者的广泛关注。由于电力系统是典型的动态系统, 状态变量随时间变化, 但是静态状态估计不考虑状态随时间变化的特点, 所以动态状态估计比静态估计更适合电力系统。目前, 关于电力系统动态估计的研究已经有很多成果, 如基于扩展卡尔曼滤波(extended Kalman filter, EKF)的动态估计算法^[4-8], 基于无迹卡尔曼滤波(unscented Kalman filter, UKF)的动态估计算法^[9-11]和基于容积卡尔曼滤波(cubature Kalman filter, CKF)的动态估计算法^[12-13]。随着区域电网的互联和电力系统规模的不断扩大, 传统的状态估计算法在估计精度和计算速度上遇到挑战, 并且不便于实施和管理, 这促进了分布式状态估计的发展^[14-19]。文献[14-15]通过对电力系统分区, 在每个区域内分别进行状态估计的迭代运算, 从而达到分布式状态估计的目的, 这样做大大地减少了运行时间, 但是邻居子系统所包含的边界节点是重叠的, 必须满足边界节点电压幅值和相角分别相等的约束条件。文献[19]基于MAP估计技术, 提出了一种新的分布式状态估计算法。该算法提高了状态估计的运算速度, 降低了通讯负担, 适用于大规模的电力系统。

本研究继续研究文献[19]中提出的分布式动态状态估计算法, 但是减弱了文献[19]所需的约束条件, 即文献[19]假设每个子系统的内部量测矩阵列满秩, 而本研究假设每个子系统是可观测的。根据这个条件和文献[19]中提供的结论, 本研究证明了由该算法得到的估计误差协方差和预测误差协方差是正定并且有上界的, 保证了算法的可行性。最后通过IEEE 39节点系统的模拟仿真, 验证了本研究的主要结果。

1 问题描述

在介绍系统模型之前, 首先给出本研究需要的一些预备知识。

考虑含有N个子系统的网络G={V, E}, 其中V={1, …, N}表示子系统代表的点集, E⊂V×V是边的集合, 假设图G是无向连通的。N_i={j∈V:(i, j)∈E}表示子系统i的邻居集合。N_i/{j}表示集合中不包含节点j。对于无环的图G, ε_i表示子系统i到图中其它任意子系统的最大路径长度。R^l表示l维实列向量的集合, R^l×q表示l×q的实矩阵的集合。为了方便, 记M^nT=(Mⁿ)^T。diag{A₁, …, A_n}表示分块对角矩阵, 对角线的元素是矩阵A₁, …, A_n。rank (A)表示矩阵A的秩。⊗表示矩阵的克罗内克积。

一个大的系统可划分成N个不重叠的子系统。每个子系统内部含有一个控制中心, 用来收集子系统的量测, 并对子系统的内部状态进行估计。每个子系统独立地并行运行算法, 这样可以极大减少运行时间, 并且可以降低所需研究的矩阵的规模。对于子系统i, 考虑如下所示的离散时间线性状态方程:

${\mathit{\boldsymbol{x}}_i}\left( {k + 1} \right) = {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{x}}_i}\left( k \right) + {\mathit{\boldsymbol{g}}_i} + {\mathit{\boldsymbol{\omega }}_i}\left( k \right),$

(1)

式中，x_i(k)∈R^n_i为子系统i在k时刻的状态; A_i∈R^n_i×n_i为定常的状态转移矩阵, 假设A_i是可逆矩阵; g_i是非零向量, 与状态轨迹的趋势相关; ω_i(k)是高斯白噪声, 其均值为0, 方差R_i≥0。假设初始状态x_i(0)是均值为x_i(0), 方差为P_i(0)>0的高斯变量。采样时间k的取值是0, 1, 2, …。

注1    在时变系统中, 利用Holt两参数线性指数平滑法^[20], 求得

$ {\boldsymbol{A}_i} = {\alpha _i}(1 + {\beta _i})\boldsymbol{I}, $

其中0 < α_i, β_i < 1。所以本文中假设A_i可逆是合理的。

子系统i的量测方程可表示成如下两类:

${\mathit{\boldsymbol{z}}_{i,i}}\left( k \right) = {\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{x}}_i}\left( k \right) + {\mathit{\boldsymbol{v}}_{i,i}}\left( k \right),$

(2)

${\mathit{\boldsymbol{z}}_{i,j}}\left( k \right) = {\mathit{\boldsymbol{B}}_{ij}}{\mathit{\boldsymbol{x}}_i}\left( k \right) + {\mathit{\boldsymbol{B}}_{ji}}{\mathit{\boldsymbol{x}}_j}\left( k \right) + {\mathit{\boldsymbol{v}}_{i,j}}\left( k \right),$

(3)

式中，z_{i, i}(k)∈R^r_ii为子系统i的内部量测; z_{i, j}(k)∈R^r_ij为连接子系统i和j的边的量测; C_i、B_ij和B_ji为具有适当维数的常矩阵; ν_{i, i}(k)和ν_{i, j}(k)是高斯白噪声, 其均值为0, 方差T_{i, i}>0和T_{i, j}>0。假设ω_i(k)、ν_{i, i}(k)、ν_{i, j}(k)和x_i(0)是互不相关的。

注2    在电力系统中, 电压(幅值和相角)可以看作是系统状态, 量测包括节点电压的幅值量测、有功功率和无功功率, 其中邻居节点都可以得到功率量测, 所以z_{i, j}(k)由子系统之间的有功功率和无功功率组成; z_{i, i}(k)由子系统内部节点的幅值量测、有功功率和无功功率组成。这也证实了本文研究的系统适用于电力系统。由于子系统i和j都可以得到边的量测(3), 所以假设z_{i, j}(k)=z_{j, i}(k)。

2 分布式状态估计算法

本文假设划分后的子系统组成的图G是无环的。

定义${{\mathit{\boldsymbol{\hat x}}}_i}\left( {k|k - 1} \right)$和Σ_i(k|k-1)分别是子系统i基于0~k-1时刻量测的状态预测和误差协方差。定义局部信息向量和信息矩阵为

$\begin{array}{l} {{\mathit{\boldsymbol{\bar \alpha }}}_i}\left( k \right) = \mathit{\boldsymbol{C}}_i^T\mathit{\boldsymbol{T}}_{i,i}^{ - 1}{\mathit{\boldsymbol{z}}_{i,i}}\left( k \right) + \sum\nolimits_i^{ - 1} {\left( {k|k - 1} \right){{\mathit{\boldsymbol{\hat x}}}_i}\left( {k|k - 1} \right)} ,\\ \;\;\;\;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\bar Q}}}_i}\left( k \right) = \mathit{\boldsymbol{C}}_i^T\mathit{\boldsymbol{T}}_{i,i}^{ - 1}{\mathit{\boldsymbol{C}}_i} + \sum\nolimits_i^{ - 1} {\left( {k|k - 1} \right).} \end{array}$

(4)

文献[19]给出的分布式MAP估计算法如下:

(1) 初始迭代

在时刻k=0, 1, 2, …, 每个子系统i计算局部的状态估计和估计误差协方差为

$ \begin{array}{l} {{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over x} }}}_{i,j}}\left( {k|k,0} \right) = \mathit{\boldsymbol{\bar Q}}_i^{ - 1}{\left( k \right)_i}{{\mathit{\boldsymbol{\bar \alpha }}}_i}\left( k \right),\\ {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \Sigma } }}_{i,j}}\left( {k|k,0} \right) = \mathit{\boldsymbol{\bar Q}}_i^{ - 1}\left( k \right); \end{array} $

同时, 子系统i计算降维的估计信息

$ \begin{array}{l} \mathit{\boldsymbol{\beta }}_j^j\left( {k,0} \right) = {\mathit{\boldsymbol{B}}_{ji}}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over x} }_{j,i}}\left( {k|k,0} \right),\\ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_j^j\left( {k,0} \right) = {\mathit{\boldsymbol{B}}_{ji}}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \Sigma } }_{j,i}}\left( {k|k,0} \right)B_{ji}^T, \end{array} $

(5)

并将该信息传递给邻居j。

(2) 循环

迭代次数h=1, 2, …, 对于子系统i,

① 根据邻居j∈N_i传递的信息β_jⁱ (k, h-1)和Φ_jⁱ (k, h-1), 子系统i更新边界量测, 得到

${y_{ji}}\left( {k,h} \right) = {z_{i,j}}\left( k \right) - \beta _j^i\left( {k,h - 1} \right),$

(6)

${S_{ji}}\left( {k,h} \right) - {T_{i,j}} + \Phi _j^i\left( {k,h - 1} \right).$

(7)

② 子系统i计算当前的状态估计和估计误差协方差

$\begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_i}\left( {k|k,h} \right) = \mathit{\boldsymbol{Q}}_i^{ - 1}\left( {k,h} \right){\mathit{\boldsymbol{\alpha }}_i}\left( {k,h} \right),\\ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i}\left( {k|k,h} \right) = \mathit{\boldsymbol{Q}}_i^{ - 1}\left( {k,h} \right) \end{array}$

(8)

式中:

${\mathit{\boldsymbol{\alpha }}_i}\left( {k,h} \right) = {{\mathit{\boldsymbol{\bar \alpha }}}_i}\left( k \right) + \sum\limits_{j \in {N_i}} {\mathit{\boldsymbol{B}}_{ij}^{\rm{T}}} \mathit{\boldsymbol{S}}_{ji}^{ - 1}\left( {k,h} \right){\mathit{\boldsymbol{y}}_{ji}}\left( {k,h} \right),$

(9)

${\mathit{\boldsymbol{Q}}_i}\left( {k,h} \right) = {{\mathit{\boldsymbol{\bar Q}}}_i}\left( k \right) + \sum\limits_{j \in {N_i}} {\mathit{\boldsymbol{B}}_{ij}^{\rm{T}}} \mathit{\boldsymbol{S}}_{ji}^{ - 1}\left( {k,h} \right){\mathit{\boldsymbol{B}}_{ji}}$

(10)

③ 同时, 子系统i得到

$ \begin{array}{l} {{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over x} }}}_{i,j}}\left( {k,h} \right) = {\left[ {\mathit{\boldsymbol{Q}}_i^j\left( {k,h} \right)} \right]^{ - 1}}\mathit{\boldsymbol{\alpha }}_i^j\left( {k,h} \right),\\ {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \Sigma } }}_{i,j}}\left( {k,h} \right) = {\left[ {\mathit{\boldsymbol{Q}}_i^j\left( {k,h} \right)} \right]^{ - 1}}, \end{array} $

式中:$\mathit{\boldsymbol{\alpha }}_i^j\left( {k,h} \right) = {{\mathit{\boldsymbol{\bar \alpha }}}_i}\left( k \right) + \sum\limits_{m \in {N_i}\left\{ j \right\}} {\mathit{\boldsymbol{B}}_{mi}^{\rm{T}}} \mathit{\boldsymbol{S}}_{mi}^{ - 1}\left( {k,h} \right){\mathit{\boldsymbol{y}}_{mi}}\left( {k,h} \right);{\rm{ }}$; $\mathit{\boldsymbol{Q}}_i^j\left( {k,h} \right) = {{\mathit{\boldsymbol{\bar Q}}}_i}\left( k \right) + \sum\limits_{m \in {N_i}\left\{ j \right\}} {\mathit{\boldsymbol{B}}_{im}^{\rm{T}}} \mathit{\boldsymbol{S}}_{mi}^{ - 1}\left( {k,h} \right){\mathit{\boldsymbol{B}}_{im}}$。并将β_i^j (k, h)和Φ_i^j (k, h)传递给邻居j。

文献[19]中的定理1已经证明了由子系统组成的图无环时, 在每个时刻k, 子系统i的状态估计迭代有限次之后收敛, 即对于所有的l≥0,

$\begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_i}\left( {k|k,{\varepsilon _i} + l} \right) = \mathit{\boldsymbol{\hat x}}_i^*\left( {k|k} \right),\\ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i}\left( {k|k,{\varepsilon _i} + l} \right) = \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right). \end{array}$

(11)

根据在时刻k得到的状态估计$\mathit{\boldsymbol{\hat x}}_i^*\left( {k|k} \right)$和估计误差协方差Σ_i^* (k|k), 可以对k+1时刻的状态进行预测。子系统i的状态预测方程为

$\begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_i}\left( {k + 1|k} \right) = {\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{\hat x}}_i^*\left( {k|k} \right) + {\mathit{\boldsymbol{g}}_i},\\ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i}\left( {k + 1|k} \right) = {\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right)\mathit{\boldsymbol{A}}_i^{\rm{T}} + {\mathit{\boldsymbol{R}}_i}. \end{array}$

(12)

3 算法的有界性

下面的两个定理证明了Σ_i^* (k|k)和Σ_i(k+1|k)有界。

定理1    在每个k时刻, 子系统i的估计误差协方差和预测误差协方差是正定的, 即

$ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right) > 0,\\ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i}\left( {k + 1|k} \right) > 0。 \end{array} $

证明    根据数学归纳法证明这个定理。当k=0并且h=0时, 根据每个子系统i的初始值Σ_i(0|-1)=P_i(0)>0和T_{i, i}>0, 得到Q_i(0)>0和${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \Sigma } }_{i,j}}$ (0|0, 0)>0。根据式(5)和(7)有S_ji(0, 1)>0。由式(10)可得Q_i(0, 1)>0, 从而得到Σ_i(0|0, 1)>0。假设该结论在h>1时成立, 即对于所有的子系统i, 有Σ_i(0|0, h)>0和 ${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \Sigma } }_{i,j}}$ (0|0, h)>0成立。当迭代次数为h+1时, 由式(5)和(7)得到S_ji(0, h+1)>0。再次根据式(10)可得Σ_i(0|0, h+1)>0。当h≥ε_i时, 根据式(11)得到Σ_i^* (0|0)>0, 并且由式(12), 显然可得Σ_i(1|0)>0。

假设在k>0时刻, 该结论成立, 即Σ_i^* (k|k)>0和Σ_i(k+1|k)>0。在k+1时刻并且h=0时, 根据式(4)每个子系统i得到Q_i(k+1)>0从而有${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \Sigma } }_{i,j}}$ (k+1|k+1, 0)>0。根据式(5)和(7), 有S_ji(k+1, 1)>0。由式(10)可得Q_i(k+1, 1)>0, 并且Σ_i(k+1|k+1, 1)>0。根据此前用到的数学归纳法可证得当h≥ε_i时, 有Σ_i^* (k+1|k+1)>0, 并且由式(12)得到Σ_i(k+2|k+1)>0。证毕。

在分布式状态估计算法中, 边量测的更新方程(6)可以写成:

${\mathit{\boldsymbol{y}}_{ji}}\left( {k,h + 1} \right) = {\mathit{\boldsymbol{B}}_{ij}}{\mathit{\boldsymbol{x}}_i}\left( k \right) + {\mathit{\boldsymbol{B}}_{ji}}\left( {{x_j}\left( k \right) - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over x} }_{j,i}}\left( {k|k,h} \right)} \right) + {\mathit{\boldsymbol{v}}_{i,j}}\left( k \right)$

(13)

式(13)右边的最后两项可以看作是量测噪声, 方差是Φ_jⁱ (k, h)+T_{i, j}。式(9)和(10)可以写成

$\begin{array}{l} {\mathit{\boldsymbol{\alpha }}_i}\left( {k,h} \right) = \mathit{\boldsymbol{H}}_i^{\rm{T}}\mathit{\boldsymbol{\bar R}}_i^{ - 1}\left( {k,h} \right){\mathit{\boldsymbol{z}}_i}\left( {k,h} \right) + \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^{ - 1}\left( {k|k - 1} \right){{\mathit{\boldsymbol{\hat x}}}_i}\left( {k|k - 1} \right),\\ {\mathit{\boldsymbol{Q}}_i}\left( {k,h} \right) = \mathit{\boldsymbol{H}}_i^{\rm{T}}\mathit{\boldsymbol{\bar R}}_i^{ - 1}\left( {k,h} \right){\mathit{\boldsymbol{H}}_i} + \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^{ - 1}\left( {k|k - 1} \right) \end{array}$

(14)

即向量z_i(k, h)由量测z_{i, i}(k)和y_ji(k, h), (j∈N_i)组成, 用来估计子系统i的状态, 矩阵H_i由C_i和B_ij组成, R_i(k, h)是分块对角矩阵, 对角线的分块矩阵分别是T_{i, i}和S_ji(k, h)。特别地, 如果子系统i拥有邻居1, …, a_i, 则z_i(k, h), H_i和R_i(k, h)具有如下形式:

$ \begin{array}{l} {\mathit{\boldsymbol{z}}_i}\left( {k,h} \right) = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{z}}_{i,i}}\left( k \right)}\\ {{\mathit{\boldsymbol{y}}_{1i}}\left( {k,h} \right)}\\ \vdots \\ {{\mathit{\boldsymbol{y}}_{{a_i}i}}\left( {k,h} \right)} \end{array}} \right),{H_i} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_i}}\\ {{\mathit{\boldsymbol{B}}_{i1}}}\\ \vdots \\ {{\mathit{\boldsymbol{B}}_{i{a_i}}}} \end{array}} \right),\\ {{\mathit{\boldsymbol{\bar R}}}_i}\left( {k,h} \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_{i,i}}}&0& \cdots &0\\ 0&{{\mathit{\boldsymbol{S}}_{1i}}\left( {k,h} \right)}& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{\mathit{\boldsymbol{S}}_{{a_i}i}}\left( {k,h} \right)} \end{array}} \right]. \end{array} $

事实上, 定理1已经证明了S_ji(k, h)>0, 所以矩阵R_i(k, h)也是正定的。定义矩阵W_i=diag{T_{i, i}, T_{i, 1}, …, T_{i, ai}}>0, 则R_i(k, h)≥W_i。

在k时刻, 当估计误差协方差收敛到Σ_i^* (k|k)时, S_ji(k, h)也是收敛的。定义矩阵${{\mathit{\boldsymbol{\tilde R}}}_i}\left( k \right) = {{\mathit{\boldsymbol{\bar R}}}_i}\left( {k,h} \right)$, h≥ε_i。根据式(8) (11)和(14), 得到

${\left( {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right)} \right)^{ - 1}} = \mathit{\boldsymbol{H}}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde R}}}_i}\left( k \right){\mathit{\boldsymbol{H}}_i} + \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^{ - 1}\left( {k|k - 1} \right).$

(15)

定义矩阵

$ \begin{array}{l} \mathit{\boldsymbol{A}} = \left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{A}}_i^{ - ({n_i} - 1)}}\\ {\mathit{\boldsymbol{A}}_i^{1 - ({n_i} - 1)}}\\ \vdots \\ \mathit{\boldsymbol{I}} \end{array}} \right),\mathit{\boldsymbol{\tilde A = }}\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{A}}_i^{ - {n_i}}}\\ {\mathit{\boldsymbol{A}}_i^{ - ({n_i} - 1)}}\\ \vdots \\ {\mathit{\boldsymbol{A}}_i^{ - 1}} \end{array}} \right),\\ \mathit{\boldsymbol{R}}\left( k \right) = \\ \left[ {\begin{array}{*{20}{c}} {{{\left( {1 + c} \right)}^{ - ({n_i} - 1)}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}(k - ({n_i} - 1))}&0& \cdots &0\\ 0&{{{\left( {1 + c} \right)}^{1 - ({n_i} - 1)}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}k + 1 - ({n_i} - 1))}& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{\mathit{\boldsymbol{\tilde R}}_i^{ - 1}\left( k \right)} \end{array}} \right], \end{array} $

其中常数c>0; k≥n_i-1。定义W_i=diag{(1+c)^-(n_i-1)W_i^-1, (1+c)^1-(n_i-1)W_i^-1, …, W_i^-1}, 则R(k)≤_i。下面的定理将证明Σ_i^* (k|k)和Σ_i(k+1|k)有上界。

定理2   假设矩阵列(A_i, H_i)完全能观测, 则存在常数c>0, 使得协方差矩阵Σ_i^*(k|k)和Σ_i(k+1|k), (k≥n_i-1), 有上界, 即

$\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right) < {\left( {{{\left( {\left( {\mathit{\boldsymbol{I}} \otimes {\mathit{\boldsymbol{H}}_i}} \right)\mathit{\boldsymbol{A}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}\left( k \right)\left( {\left( {\mathit{\boldsymbol{I}} \otimes \mathit{\boldsymbol{H}}} \right)\mathit{\boldsymbol{A}}} \right)} \right)^{ - 1}},$

(16)

$\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^{ - 1}\left( {k + 1|k} \right) < {\left( {{{\left( {\left( {\mathit{\boldsymbol{I}} \otimes \mathit{\boldsymbol{H}}} \right)\mathit{\boldsymbol{\tilde A}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}\left( k \right)\left( {\left( {\mathit{\boldsymbol{I}} \otimes \mathit{\boldsymbol{H}}} \right)\mathit{\boldsymbol{\tilde A}}} \right)} \right)^{ - 1}} + {\mathit{\boldsymbol{R}}_i}.$

(17)

证明    定理1已证明在每个时刻k, 子系统i的估计误差协方差Σ_i^* (k|k)>0。由于R_i≥0并且A_i可逆, 则存在常数c>0使得

${\mathit{\boldsymbol{R}}_i} \le c{\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right)\mathit{\boldsymbol{A}}_i^{\rm{T}}$

(18)

由式(15)(18), 得到

${\left( {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right)} \right)^{ - 1}} \ge \mathit{\boldsymbol{H}}_i^{\rm{T}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}\left( k \right){\mathit{\boldsymbol{H}}_i} + {\left( {\left( {1 + c} \right){\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k - 1|k - 1} \right)\mathit{\boldsymbol{A}}_i^{\rm{T}}} \right)^{ - 1}}.$

(19)

将式(19)两端同时乘以A_i^T和A_i, 并根据A_i可逆, 得到

$\mathit{\boldsymbol{A}}_i^{\rm{T}}{\left( {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right)} \right)^{ - 1}}{\mathit{\boldsymbol{A}}_i} \ge \mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{H}}_i^{\rm{T}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}\left( k \right){\mathit{\boldsymbol{H}}_i}{\mathit{\boldsymbol{A}}_i} + {\left( {\left( {1 + c} \right){\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k - 1|k - 1} \right)} \right)^{ - 1}}.$

(20)

类似地, 在k-1时刻, 可得

$\mathit{\boldsymbol{A}}_i^{\rm{T}}{\left( {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k - 1|k - 1} \right)} \right)^{ - 1}}{\mathit{\boldsymbol{A}}_i} \ge \mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{H}}_i^{\rm{T}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}\left( {k - 1} \right) \\ {\mathit{\boldsymbol{H}}_i}{\mathit{\boldsymbol{A}}_i} + {\left( {\left( {1 + c} \right)\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k - 2|k - 2} \right)} \right)^{ - 1}}.$

(21)

将式(20)和(21)结合, 得到

$ \begin{array}{l} \mathit{\boldsymbol{A}}_i^{2{\rm{T}}}{(\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right))^{ - 1}}\mathit{\boldsymbol{A}}_i^2 \ge \mathit{\boldsymbol{A}}_i^{2{\rm{T}}}\mathit{\boldsymbol{H}}_i^{\rm{T}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}\left( k \right){\mathit{\boldsymbol{H}}_i}\mathit{\boldsymbol{A}}_i^2 + {\left( {1 + c} \right)^{ - 1}}\\ \mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{H}}_i^{\rm{T}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}\left( {k - 1} \right){\mathit{\boldsymbol{H}}_i}{\mathit{\boldsymbol{A}}_i} + {\left( {1 + c} \right)^{ - 2}}{(\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k - 2|k - 2} \right))^{ - 1}}。 \end{array} $

继续进行, 得到

$ \begin{array}{l} \mathit{\boldsymbol{A}}_i^{({n_i} - 1){\rm{T}}}{\left( {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right)} \right)^{ - 1}}\mathit{\boldsymbol{A}}_i^{{n_i} - 1} \ge \mathit{\boldsymbol{A}}_i^{({n_i} - 1){\rm{T}}}\mathit{\boldsymbol{H}}_i^{\rm{T}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}\left( k \right){\mathit{\boldsymbol{H}}_i}\mathit{\boldsymbol{A}}_i^{{n_i} - 1} + {\left( {1 + c} \right)^{ - 1}}\\ \mathit{\boldsymbol{A}}_i^{({n_i} - 2){\rm{T}}}\mathit{\boldsymbol{H}}_i^{\rm{T}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}\left( {k - 1} \right){\mathit{\boldsymbol{H}}_i}\mathit{\boldsymbol{A}}_i^{{n_i} - 2} + \cdots + {\left( {1 + c} \right)^{ - ({n_i} - 2)}}\mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{H}}_i^{\rm{T}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}\left( {k - {n_i} + 2} \right){\mathit{\boldsymbol{H}}_i}{\mathit{\boldsymbol{A}}_i} + \\ {\left( {1 + c} \right)^{ - ({n_i} - 1)}}{\left( {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k - {n_i} + 1|k - {n_i} + 1} \right)} \right)^{ - 1}}。 \end{array} $

由于

$ \begin{array}{l} {\left( {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k - {n_i} + 1|k - {n_i} + 1} \right)} \right)^{ - 1}} = \\ \mathit{\boldsymbol{H}}_i^{\rm{T}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}\left( {k - {n_i} + 1} \right){\mathit{\boldsymbol{H}}_i} + \sum _i^{ - 1}\left( {k - {n_i} + 1|k - {n_i} + 1} \right), \end{array} $

并且定理1已经证明了Σ_i^-1 (k-n_i+1|k-n_i)>0, k≥n_i-1, 得到

$\mathit{\boldsymbol{A}}_i^{\left( {{n_i} - 1} \right){\rm{T}}}{\left( {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right)} \right)^{ - 1}}\mathit{\boldsymbol{A}}_i^{{n_i} - 1} > \sum\limits_{l = 0}^{{n_i} - 1} {{{\left( {1 + c} \right)}^{l - \left( {{n_i} - 1} \right)}}} \\ {\left( {{\mathit{\boldsymbol{H}}_i}\mathit{\boldsymbol{A}}_i^l} \right)^{\rm{T}}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}\left( {k + l - \left( {{n_i} - 1} \right)} \right){\mathit{\boldsymbol{H}}_i}\mathit{\boldsymbol{A}}_i^l.$

(22)

将式(22)两端分别乘以A_i^{-(n_i-1) T}和A_i^-(n_i-1), 可得

$ \begin{array}{l} {(\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right))^{ - 1}} > \sum\limits_{l = 0}^{{n_i} - 1} {{{\left( {1 + c} \right)}^{l - ({n_i} - 1)}}} {({\mathit{\boldsymbol{H}}_i}\mathit{\boldsymbol{A}}_i^{l - ({n_i} - 1)})^{\rm{T}}}\mathit{\boldsymbol{\tilde R}}_i^{ - 1}(k + l - ({n_i} - 1))\\ {\mathit{\boldsymbol{H}}_i}\mathit{\boldsymbol{A}}_i^{l - ({n_i} - 1)} = {((\mathit{\boldsymbol{I}} \otimes {\mathit{\boldsymbol{H}}_i})\mathit{\boldsymbol{A}})^{\rm{T}}}\mathit{\boldsymbol{R}}\left( k \right)((\mathit{\boldsymbol{I}} \otimes {\mathit{\boldsymbol{H}}_i})\mathit{\boldsymbol{A}})。 \end{array} $

因为(A_i, H_i)是可观测的, A_i可逆, 并且R(k)正定, 有

$ \begin{array}{c} {\rm{rank}}((\mathit{\boldsymbol{I}} \otimes {\mathit{\boldsymbol{H}}_i})\mathit{\boldsymbol{A}}) = {n_i},\\ {((\mathit{\boldsymbol{I}} \otimes {\mathit{\boldsymbol{H}}_i})\mathit{\boldsymbol{A}})^{\rm{T}}}\mathit{\boldsymbol{R}}\left( k \right)((\mathit{\boldsymbol{I}} \otimes {\mathit{\boldsymbol{H}}_i})\mathit{\boldsymbol{A}}) > 0, \end{array} $

则得到式(16)。根据式(12)和(16), 得到

$ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }} _i}\left( {k + 1|k} \right) < {\mathit{\boldsymbol{A}}_i}{\left( {{{((\mathit{\boldsymbol{I}} \otimes {\mathit{\boldsymbol{H}}_i})\mathit{\boldsymbol{A}})}^{\rm{T}}}\mathit{\boldsymbol{R}}\left( k \right)((\mathit{\boldsymbol{I}} \otimes {\mathit{\boldsymbol{H}}_i})\mathit{\boldsymbol{A}})} \right)^{ - 1}}\mathit{\boldsymbol{A}}_i^{\rm{T}} + {\mathit{\boldsymbol{R}}_i}, $

从而可得式(17)。证毕。

注3    文献[19]假设每个子系统的内部量测矩阵C_i列满秩, 而本文需要条件(A_i, H_i)完全能观测即可, 这表明本文的条件减弱了文献[19]所需的条件, 但是该条件仍然可以保证误差协方差矩阵正定并且有上界, 从而保证了算法的可行性。

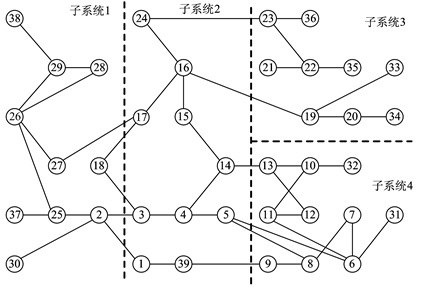
4 仿真实例

如图 1所示, IEEE 39节点系统被分为4个不重叠的子系统, 每个子系统分别包含10、10、10和9个节点, 并且划分后的图是无环的, 这满足本文的假设条件。划分后的图的直径是2, 文献[19]中的定理1已经证明该算法在每个时刻迭代2次后即可收敛, 所以为了得到Σ_i^* (k|k), 在仿真时每个时刻迭代2次。

系统中每个节点s的系统参数如下:

$ {\mathit{\boldsymbol{A}}_s} = \left[ {\begin{array}{*{20}{c}} {0.84}&0\\ 0&{0.87} \end{array}} \right],{\mathit{\boldsymbol{C}}_s} = \left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right],{\mathit{\boldsymbol{B}}_{ss'}} = {\mathit{\boldsymbol{B}}_{s's}} = \left[ {\begin{array}{*{20}{c}} {2.35}&{1.17}\\ { - 0.83}&{1.64} \end{array}} \right], $

式中s′∈N_s。并假设R_s=0.03²I, T_{s, s}=0.01²I, T_{s, s′}=0.02²I。将每个子系统所包含节点的参数结合起来即可得到子系统i的系统(1)(2)和(3)中的参数。

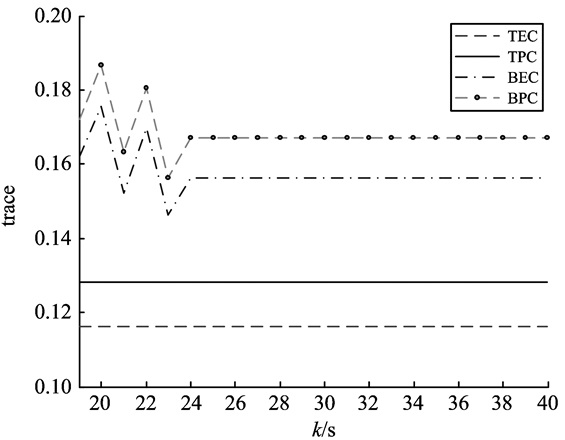
仿真的目的是根据该算法得到的误差协方差的迹来验证定理1和定理2的结论。误差协方差的迹分别表示为$\sum\limits_{i = 1}^4 {{\rm{Tr}}} \left\{ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^*\left( {k|k} \right)} \right\}({\rm{TEC}})$和$\sum\limits_{i = 1}^4 {{\rm{Tr}}} \left\{ {{\Sigma _i}\left( {k + 1|k} \right)} \right\}({\rm{TPC}})$, 其上界分别表示为BEC和BPC。TEC和TPC随时间的变化曲线如图 2所示。由于子系统的最大维数是20, 并且定理2必须满足k≥n_i-1, 所以误差协方差的上界从k=19开始得到, 而之前有限时间的结果都是有界的。误差协方差的迹及其上界的变化曲线如图 3所示。从图 2、3可以看出, 该算法得到的误差协方差是正定有界的, 并且严格小于给定的上界, 验证了本研究的主要结果。

5 结语

本研究讨论的动态系统适用于很多实际应用, 例如电力系统、传感器网络、多智能体系统等。主要目的是继续研究文献[19]提出的分布式状态估计算法, 通过将限制条件减弱为每个子系统可观测, 证明得到的误差协方差矩阵是正定并且有上界的, 保证了该算法在实际应用中的有效性和可行性, 可作为电力系统动态状态估计的有效方法。IEEE 39节点系统的模拟仿真验证了本研究的主要结论。下一步将研究非线性的时变系统, 给出新的分布式状态估计算法, 并且对模型参数进行辨识, 进一步优化算法, 得到误差协方差矩阵有界的结论。