2. 广西可信软件重点实验室, 广西 桂林 541004
2. Guangxi Key Laboratory of Trusted Software, Guilin 541004, Guangxi, China
“互联网+”使在线旅游业发展加速, 人们登陆旅游网站查看景点信息, 浏览其他用户对景点的评分、上传的照片或者游记等信息, 这极大地方便和丰富了用户对景点的选择。但是, 在线旅游业的飞速发展导致日益严重的信息过载现象[1], 信息的庞繁降低了用户做出旅游决策的效率。
推荐系统根据用户以往在网上留下的点击、浏览、评分等信息来建立用户行为模型, 分析其旅游偏好, 进而为其提供个性化的旅游推荐。很多旅游网站保存了用户关注的人及粉丝, 景点的类型标签, 用户对景点的评分信息等。不少研究利用这些信息来改进对用户推荐景点的算法。文益民等人从个性化旅游推荐的概念、内容、方法、用到的数据、实际应用以及其面临的挑战综合阐述了个性化旅游推荐的进展[2]。史一帆等人利用旅游网站上景点的标签信息及用户间的相互关注信息来改进传统的协同过滤推荐算法[3]。雷震等人根据用户对景点的评论分析用户的情感极性, 判断用户是否真正喜欢某个景点[4]。庞俊涛等人将用户对景点在多个方面评分看作用户对景点总体评分的上下文, 来改进对总体评分的预测[5]。MAGID等人从Flickr网站上用户分享的带有地理和时间标记的照片中提取用户的旅游偏好[6]。
近年来, 传统的协同过滤推荐算法[7]被应用于各个领域[3, 8-10], 成为推荐领域使用最广泛的方法之一。基于用户的协同过滤推荐算法最早是由GOLDBERG等人在构建Tapestry邮件过滤系统时提出的[7], 后来被GropLens用于向用户推荐新闻[11]; 基于物品的协同过滤推荐算法最早由SARWAR等人提出[12], 后来被亚马逊网站用于为用户推荐商品[8]。从传统的协同过滤推荐算法提出到现在, 不断有人尝试去改进。CHOI等人将其他物品与目标物品的相似性作为权重加入用户间相似性的计算[13]。LIU等人将用户评分的均值和方差作为用户的评分偏好来改进用户间相似性的计算[14]。ZHANG等人提出了利用物品的领域特征来构建用户对领域特征的偏好向量, 然后综合用户对物品的评分向量和对物品领域特征的偏好向量计算用户间的相似性[15]。YU等人利用相似性和信任度的加权取值(称为混合相似性)替代传统协同过滤推荐中的相似性来做预测[16]。CHANG等人针对MovieLens电影数据集中的电影评分及类型标签为用户建立了两个模型, 一个是用户观看各类电影比例的模型, 另一个是用户观看每类电影的平均评分模型, 利用这两个模型计算的用户间的相似性[17]。文俊浩等人提出了考虑用户共同评分物品占所有评分物品比例的Tanimoto系数, 并与传统的协同过滤计算的相似性融合, 使推荐更准确[18]。BREESE等人提出了反用户频率, 在计算用户间相似性时降低用户评分向量中那些被很多用户评过分的流行物品的影响[19]。项亮参考文献[19]提出的反用户频率, 给出了相似度计算具体实现并在Movielens数据集上验证了算法的效果[20]。李聪等人针对用户评分数据稀疏性和推荐实时性问题, 将用户间评分项并集中非目标用户区分为有推荐能力和无推荐能力用户[21]。以上这些方法仅利用了用户对物品的总体评分信息, 但总体评分结果的原因则不尽相同。比如:两个用户都对一个物品给了总体评分值为5的高分来表达他们对这个物品的喜欢。但实际原因可能是一个用户认为这个物品稀有, 具有收藏价值, 所以给了高分; 而另一个用户则是因为喜欢这个物品的颜色, 所以比较满意给了高分。因此, 从总体评分来看这两个用户似乎对该物品的喜好相同, 但实际则是不同。这反映出总体评分有时很难准确体现用户对物品的喜好程度。
在携程网等流行的在线旅游平台上, 用户对旅游景点的评分数据中不仅有用户对景点的总体评分, 还有用户对景点在景色、趣味性、性价比这些方面的评分。利用这些评分是否能够更准确地表达用户对景点的喜好?针对该问题, 本文提出了一种基于多方面评分的景点协同推荐算法。该方法综合利用用户对景点在景色、趣味性、性价比方面的评分改进了用户和景点相似性的计算, 再根据用户或者景点间的相似性预测目标用户对目标景点的总体评分。
1 基于多方面评分的景点协同推荐 1.1 评分表示与预测在旅游网站的景点评论模块中, 注册用户可以通过对景点评分来表达满意程度。不少旅游网站上用户不仅可以给出景点一个总体评分, 还可以给出景点多个方面的评分, 如在携程网上有用户对景点的总体评分, 也有对景点在景色、趣味性、性价比方面的评分。
1.1.1 构建用户-景点评分矩阵利用用户对景点的总体评分、景色方面评分、趣味性方面评分、性价比方面评分信息可以构建用户-景点评分矩阵
| $ {\mathit{\boldsymbol{R}}_{m,n}} = \\ \left[ {\begin{array}{*{20}{c}} {\left( {{r_{1,1,1}},{r_{1,1,2}},{r_{1,1,3}},{r_{1,1,4}}} \right)}&{\left( {{r_{1,2,1}},{r_{1,2,2}},{r_{1,2,3}},{r_{1,2,4}}} \right)}& \cdots &{\left( {{r_{1,n,1}},{r_{1,n,2}},{r_{1,n,3}},{r_{1,n,4}}} \right)}\\ {\left( {{r_{2,1,1}},{r_{2,1,2}},{r_{2,1,3}},{r_{2,1,4}}} \right)}&{\left( {{r_{2,2,1}},{r_{2,2,2}},{r_{2,2,3}},{r_{2,2,4}}} \right)}& \cdots &{\left( {{r_{2,n,1}},{r_{2,n,2}},{r_{2,n,3}},{r_{2,n,4}}} \right)}\\ \vdots & \vdots & \ldots & \vdots \\ {\left( {{r_{m,1,1}},{r_{m,1,2}},{r_{m,1,3}},{r_{m,1,4}}} \right)}&{\left( {{r_{m,2,1}},{r_{m,2,2}},{r_{m,2,3}},{r_{m,2,4}}} \right)}& \cdots &{\left( {{r_{m,n,1}},{r_{m,n,2}},{r_{m,n,3}},{r_{m,n,4}}} \right)} \end{array}} \right] $ | (1) |
式中: m为用户数; n为景点数; ri, j, 1为用户i对景点j的总体评分, ri, j, 2、ri, j, 3、ri, j, 4分别为用户i对景点j在景色、趣味性、性价比方面的评分。如果用户i对景点j没有评分, 将ri, j, 1、ri, j, 2、ri, j, 3、ri, j, 4的值赋为0。
1.1.2 评分预测基于用户相似性的评分预测, 如式(2):
| $ {\rm{pred}}\left( {u,s} \right) = {{\bar r}_{u,1}} + \frac{{\sum\limits_{u' \in {U_{{\rm{sim}}}}\left( u \right)} {{\rm{sim}}} \left( {u,u'} \right) \cdot \left( {{r_{u',s,1}} - {{\bar r}_{u',1}}} \right)}}{{\sum\limits_{u' \in {U_{{\rm{sim}}}}\left( u \right)} {{\rm{sim}}} \left( {u,u'} \right)}} $ | (2) |
式中:ru, 1为用户u对其已评分景点总体评分的平均值; Usim(u)为与用户u相似性大于0的用户集合; u′为其中的一个用户; sim (u, u′)为用户u与用户u′的相似性; pred (u, s)给出目标用户u对目标景点s的总体评分的预测。
基于物品相似性的评分预测, 如式(3):
| $ {\rm{pred}}\left( {u,s} \right) = \frac{{\sum\limits_{\mathit{s}' \in {S_{{\rm{sim}}}}\left( s \right)} {{\rm{sim}}} \left( {\mathit{s},\mathit{s}'} \right) \cdot \left( {{r_{u',s,1}} - {{\bar r}_{u,s',1}}} \right)}}{{\sum\limits_{\mathit{s}' \in {S_{{\rm{sim}}}}\left( s \right)} {{\rm{sim}}} \left( {\mathit{s},\mathit{s}'} \right)}} $ | (3) |
式中:Ssim(s)为与景点s相似性大于0的景点集合; s′为其中的一个景点; sim (s, s′)为景点s与景点s′的相似性。
1.2 基于多方面评分的相似性计算由于用户对景点不再只有一个总体评分, 还有对景点多个方面的评分, 利用这些评分可设计多种计算用户或物品间相似性的方法。
1.2.1 用户间相似性计算方法| $ {\rm{si}}{{\rm{m}}_1}\left( {a,b} \right) = \frac{{\sum\limits_{s \in S} {\left( {{r_{a,s,1}} - {{\bar r}_{a,1}}} \right)\left( {{r_{\mathit{b},s,1}} - {{\bar r}_{\mathit{b},1}}} \right)} }}{{\sqrt {\sum\limits_{s \in S} {{{\left( {{r_{a,s,1}} - {{\bar r}_{a,1}}} \right)}^2}} } \sqrt {\sum\limits_{s \in S} {{{\left( {{r_{\mathit{b},s,1}} - {{\bar r}_{\mathit{b},1}}} \right)}^2}} } }} $ | (4) |
| $ {\rm{si}}{{\rm{m}}_{2,k}}\left( {a,b} \right) = \frac{{\sum\limits_{s \in S} {\left( {{r_{a,s,\mathit{k}}} - {{\bar r}_{a,\mathit{k}}}} \right)\left( {{r_{\mathit{b},s,\mathit{k}}} - {{\bar r}_{\mathit{b},\mathit{k}}}} \right)} }}{{\sqrt {\sum\limits_{s \in S} {{{\left( {{r_{a,s,\mathit{k}}} - {{\bar r}_{a,\mathit{k}}}} \right)}^2}} } \sqrt {\sum\limits_{s \in S} {{{\left( {{r_{\mathit{b},s,\mathit{k}}} - {{\bar r}_{\mathit{b},\mathit{k}}}} \right)}^2}} } }}, $ | (5) |
| $ {\rm{si}}{{\rm{m}}_3}\left( {a,b} \right) = \frac{1}{{{\rm{len}}\left( S \right)}}\sum\limits_{s \in S} {\frac{{\sum\limits_{k = 2}^4 {\left( {{r_{a,s,\mathit{k}}} - {{\bar r}_{a,s}}} \right)\left( {{r_{\mathit{b},s,\mathit{k}}} - {{\bar r}_{\mathit{b},s}}} \right)} }}{{\sqrt {\sum\limits_{k = 2}^4 {{{\left( {{r_{a,s,\mathit{k}}} - {{\bar r}_{a,s}}} \right)}^2}} } \sqrt {\sum\limits_{k = 2}^4 {{{\left( {{r_{\mathit{b},s,\mathit{k}}} - {{\bar r}_{\mathit{b},\mathit{s}}}} \right)}^2}} } }}} , $ | (6) |
| $ {\rm{si}}{{\rm{m}}_4}\left( {a,b} \right) = \frac{{\sum\limits_{s \in S} {\sum\limits_{k = 2}^4 {\left( {{r_{a,s,\mathit{k}}} - {{\bar r}_a}} \right)\left( {{r_{\mathit{b},s,\mathit{k}}} - {{\bar r}_\mathit{b}}} \right)} } }}{{\sqrt {\sum\limits_{s \in S} {\sum\limits_{k = 2}^4 {{{\left( {{r_{a,s,\mathit{k}}} - {{\bar r}_a}} \right)}^2}} } } \sqrt {\sum\limits_{s \in S} {\sum\limits_{k = 2}^4 {{{\left( {{r_{\mathit{b},s,\mathit{k}}} - {{\bar r}_b}} \right)}^2}} } } }} $ | (7) |
| $ {\rm{si}}{{\rm{m}}_5}\left( {a,b} \right) = \frac{{\sum\limits_{s \in S} {\left( {\left( {{r_{a,s,1}} - {{\bar r}_{a,1}}} \right)\left( {{r_{\mathit{b},s,1}} - {{\bar r}_{\mathit{b},1}}} \right)*itempop\left( s \right)} \right)} }}{{\sqrt {\sum\limits_{s \in S} {{{\left( {{r_{a,s,1}} - {{\bar r}_{a,1}}} \right)}^2}} } \sqrt {\sum\limits_{s \in S} {{{\left( {{r_{\mathit{b},s,1}} - {{\bar r}_{\mathit{b},1}}} \right)}^2}} } }} $ | (8) |
| $ {\rm{si}}{{\rm{m}}_6}\left( {a,b} \right) = \frac{1}{{{\rm{len}}\left( S \right)}}\sum\limits_{s \in S} {\left( {\frac{{\sum\limits_{k = 2}^4 {\left( {{r_{a,s,k}} - {{\bar r}_{a,s}}} \right)\left( {{r_{\mathit{b},s,k}} - {{\bar r}_{\mathit{b},s}}} \right)} }}{{\sqrt {\sum\limits_{k = 2}^4 {\left( {{r_{a,s,k}} - {{\bar r}_{a,s}}} \right)} } \sqrt {\sum\limits_{k = 2}^4 {\left( {{r_{\mathit{b},s,k}} - {{\bar r}_{\mathit{b},s}}} \right)} } }}*{\rm{itempop}}\left( s \right)} \right)} , $ | (9) |
| $ {\rm{itempop}}\left( s \right) = \frac{1}{{\ln \left( {1 + N\left( s \right)} \right)}}. $ | (10) |
式中: a、b为用户; S为用户a和用户b共同评分的景点集合; s为其中的一个景点; len (S)为该集合的大小; N(s)为对景点s有评分的用户数; ra, 1、rb, 1分别为用户a和用户b对其已评分景点总体评分的平均值; ra, s、rb, s分别为用户a和用户b对景点s在景色、趣味性、性价比三方面的平均评分; ra、rb分别为用户a和用户b对其已评分景点在景色、趣味性、性价比方面的平均评分。itempop (s)的计算公式取自文献[20]。式(4)利用总体评分计算用户间相似性; 式(5)分别利用景色、趣味性、性价比评分计算用户间的相似性; 式(6)和式(7)综合利用用户对景点在景色、趣味性、性价比三个方面评分计算用户间的相似性; 式(8)利用总体评分和景点的流行度[20]计算用户间的相似性; 式(9)综合利用用户对景点在景色、趣味性、性价比三个方面评分和景点的流行度计算用户间的相似性。
1.2.2 景点间相似性计算方法| $ {\rm{si}}{{\rm{m}}_7}\left( {s,t} \right) = \frac{{\sum\limits_{u \in U} {\left( {{r_{\mathit{u},s,1}} - {{\bar r}_{s,1}}} \right)\left( {{r_{\mathit{u},t,1}} - {{\bar r}_{t,1}}} \right)} }}{{\sqrt {\sum\limits_{u \in U} {{{\left( {{r_{\mathit{u},s,1}} - {{\bar r}_{s,1}}} \right)}^2}} } \sqrt {\sum\limits_{u \in U} {{{\left( {{r_{\mathit{u},t,1}} - {{\bar r}_{t,1}}} \right)}^2}} } }}, $ | (11) |
| $ {\rm{si}}{{\rm{m}}_{8,k}}\left( {s,t} \right) = \frac{{\sum\limits_{u \in U} {\left( {{r_{\mathit{u},s,\mathit{k}}} - {{\bar r}_{s,\mathit{k}}}} \right)\left( {{r_{\mathit{u},t,\mathit{k}}} - {{\bar r}_{t,\mathit{k}}}} \right)} }}{{\sqrt {\sum\limits_{u \in U} {{{\left( {{r_{\mathit{u},s,\mathit{k}}} - {{\bar r}_{s,\mathit{k}}}} \right)}^2}} } \sqrt {\sum\limits_{u \in U} {{{\left( {{r_{\mathit{u},t,\mathit{k}}} - {{\bar r}_{t,\mathit{k}}}} \right)}^2}} } }},\mathit{k = }{\rm{2,3,4,}} $ | (12) |
| $ {\rm{si}}{{\rm{m}}_{9}}\left( {s,t} \right) = \frac{1}{3}\sum\limits_{k = 2}^1 {\frac{{\sum\limits_{u \in U} {\left( {{r_{\mathit{u},s,\mathit{k}}} - {{\bar r}_{s,\mathit{k}}}} \right)\left( {{r_{\mathit{u},t,\mathit{k}}} - {{\bar r}_{t,\mathit{k}}}} \right)} }}{{\sqrt {\sum\limits_{u \in U} {{{\left( {{r_{\mathit{u},s,\mathit{k}}} - {{\bar r}_{s,\mathit{k}}}} \right)}^2}} } \sqrt {\sum\limits_{u \in U} {{{\left( {{r_{\mathit{u},t,\mathit{k}}} - {{\bar r}_{t,\mathit{k}}}} \right)}^2}} } }}} , $ | (13) |
| $ {\rm{si}}{{\rm{m}}_{10}}\left( {s,t} \right) = \frac{{\sum\limits_{u \in U} {\sum\limits_{k = 2}^4 {\left( {{r_{\mathit{u},s,\mathit{k}}} - {{\bar r}_{s,\mathit{k}}}} \right)\left( {{r_{\mathit{u},t,\mathit{k}}} - {{\bar r}_{t,\mathit{k}}}} \right)} } }}{{\sqrt {\sum\limits_{u \in U} {{{\sum\limits_{k = 2}^4 {\left( {{r_{\mathit{u},s,\mathit{k}}} - {{\bar r}_{s,\mathit{k}}}} \right)} }^2}} } \sqrt {\sum\limits_{u \in U} {{{\sum\limits_{k = 2}^4 {\left( {{r_{\mathit{u},t,\mathit{k}}} - {{\bar r}_t}} \right)} }^2}} } }}, $ | (14) |
式中:s、t为景点; U为景点s和景点t共同评分的用户集合; u为其中的一个用户; rs, 1、rt, 1分别为用户集U中的用户对景点s和景点t总体评分的平均值; rs, k、rt, k分别为用户集U中的用户对景点s和景点t在第k个方面评分的平均值; rs、rt分别为用户集U中的用户对景点s和景点t在景色、趣味性、性价比方面所有评分的平均值。式(11)利用总体评分计算物品间的相似性; 式(12)分别利用景色、趣味性、性价比评分计算物品间的相似性; 式(13)和式(14)综合利用用户对景点在景色、趣味性、性价比三个方面的评分计算物品间的相似性。
2 试验方案设计 2.1 试验数据集本研究从旅游服务网站携程网(http://www.ctrip.com)上抓取桂林、杭州、上海3个城市的景点, 收集了用户对这些景点的总体评分信息以及在景色、趣味性、性价比三个方面的景点评分信息。桂林旅游数据集包括163个景点、16 532个用户、用户对景点的30 969条评分记录; 杭州旅游数据集包括210个景点、42 459个用户、用户对景点的71 112条评分记录; 上海旅游数据集包括270个景点、72 548个用户、用户对景点的149 147条评分记录。
图 1为携程网上用户对景点的评分实例, 图 2为从携程网上抓取用户对景点评分数据后存储在文本文件中的样本示例。

|
图 1 用户对景点的评分的网上实例 Figure 1 The example of user's rating for a scenery |
|
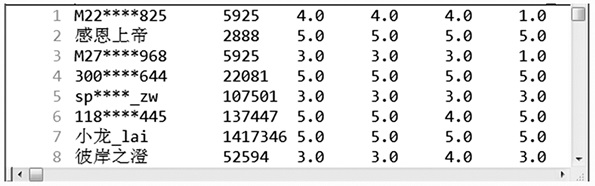
图 2 从携程网采集到的用户对景点的评分信息 Figure 2 User's rating for sceneries crawled from XieCheng website |
图 1中用户陆小凤对景点阳朔的总体评分为4, 在景色、趣味性、性价比方面的评分分别为4、3、3;图 2中每条记录代表一个用户对一个景点的所有评分信息, 如第1条记录“M22****825 5925 4.0 4.0 4.0 1.0”代表用户M22****825对景点5925的总体评分为4.0, 在景色方面评分为4.0, 在趣味性方面评分为4.0, 在性价比方面评分为1.0。
2.2 数据预处理为了方便试验, 对数据进行以下处理:
(1) 删除重复的用户评分记录, 选择用户对景点的最近评分作为该用户对该景点的评分;
(2) 删除只有1~2条评分记录的用户;
(3) 删除没有用户评分的景点。
经过预处理后, 桂林旅游数据集最终包括162个景点、2 189个用户、用户对景点的11 143条评分记录; 杭州旅游数据集最终包括210个景点、3 009个用户、用户对景点的17 927条评分记录; 上海旅游数据集最终包括270个景点、7 074个用户、用户对景点的46 962条评分记录。
2.3 评测指标为了检验提出的基于多方面评分的相似性计算方法的效果, 采用了最常见的5个指标对试验结果进行评估:均方根误差、平均绝对误差、覆盖率、准确率和F-度量。
(1) 均方根误差(root-mean-square error, RMSE)
| $ {\rm{RMSE = }}\sqrt {\frac{{\sum\limits_{\left( {{u_j},{s_j}} \right) \in E} {{{\left( {{r_{ij}} - {{\hat r}_{ij}}} \right)}^2}} }}{{\left| E \right|}}} . $ | (15) |
(2) 平均绝对误差(mean-absolute error, MAE)
| $ {\rm{MAE = }}\frac{1}{{\left| E \right|}}\sum\limits_{\left( {{u_j},{s_j}} \right) \in E} {\left| {{r_{ij}} - {{\hat r}_{ij}}} \right|} , $ | (16) |
式中:E为测试集; |E|为集合中元素的个数; (ui, sj)表示一个用户-景点对; rij为用户ui对景点sj的真实评分; rij为用户ui对景点sj的预测评分。均方根误差和平均绝对误差越小, 预测评分与真实评分的差距也越小, 推荐效果就越好。
(3) 覆盖率(coverage)
| $ {\rm{coverage = }}\frac{k}{M}, $ | (17) |
式中:k为能够计算预测评分的用户-景点对数, M为用户对景点有总体评分的数量。在本研究中, 如果预测评分不为0, 则认为用户对景点的评分能够预测; 如果预测评分为0, 则认为用户对景点的评分不能够预测。覆盖率描述的就是预测评分不为0的样本数占总样本数的比例, 覆盖率越高, 推荐效果就越好。
(4) 准确率(precision):
| $ {\rm{precision = 1 - }}\frac{{{\rm{RMSE}}}}{4}. $ | (18) |
式(18)是利用文献[3]中将均方根误差映射为准确率的方法, RMSE的值越小, 准确率就越大, 推荐效果也越好。
(5) F-度量(F-measure):
| $ F - {\rm{measure}} = \frac{{2 \times {\rm{precision}} \times {\rm{coverage}}}}{{{\rm{precision}} + {\rm{coverage}}}}. $ | (19) |
有时准确率和覆盖率二者会相互矛盾, 如有时准确率的提升是以减小覆盖率为代价, 或者提高覆盖率时准确率却下降。因此本研究采用了F-度量这一综合评价指标来权衡准确率和覆盖率。F-度量越大, 推荐效果也就越好。
2.4 对比试验设计采用留一交叉验证方法(leap-one-out cross validation)[3]对算法进行验证。留一交叉验证方法循环利用整个数据集中的一条数据作为测试集, 其他数据作为训练集, 直到每一条数据都作为一次测试数据, 之后综合每条数据的真实值和预测值计算各评测指标。为验证利用用户对景点在景色、趣味性、性价比三个方面评分来计算用户间和物品间的相似度的有效性, 设计了如下对比试验。
第一组和第二组对比试验基于用户间的相似性, 预测目标用户对目标物品的总体评分:
Ucf_global:利用式(4)计算用户间相似性;
Ucf_scenery:利用式(5)(k=2)计算用户间相似性;
Ucf_interest:利用式(5)(k=3)计算用户间相似性;
Ucf_price:利用式(5)(k=4)计算用户间相似性;
Ucf_sip1:利用式(6)计算用户间相似性;
Ucf_sip2:利用式(7)计算用户间相似性。
第二组对比试验为:
Ucf_itempop:利用式(8)计算用户间相似性;
Ucf_itempop_sip1:利用式(9)计算用户间相似性。
第三组试验基于物品间相似性, 预测目标用户对目标物品的总体评分:
Icf_global:利用式(11)计算物品间相似性;
Icf_scenery:利用式(12)(k=2)计算物品间相似性;
Icf_interest:利用式(12)(k=3)计算物品间相似性;
Icf_price:利用式(12)(k=4)计算物品间相似性;
Icf_sip1:利用式(13)计算物品间相似性;
Icf_sip2:利用式(14)计算物品间相似性。
3 试验结果与分析试验结果如表 1~3所示。表 1~3分别给出了每组对比试验在均方根误差、平均绝对误差、覆盖率、准确率、F-度量这5个指标上的试验结果。从表 1中可以看出, 综合了3个方面评分的Ucf_sip1、Ucf_sip2方法在3个城市的旅游数据集的5个指标上均优于只单独考虑景色、趣味性、性价比的Ucf_scenery、Ucf_interest、Ucf_price算法及利用总评分计算用户相似性的Ucf_global方法。从表 2也看到, Ucf_pop_sip1算法在5个指标上均优于Ucf_pop, 这说明利用用户对景点多个方面的评分信息能有效改善用户间相似性的计算。分析原因为:若两个用户对一个景点的评价在多个方面越相似, 那么用户间的相似性也越大; 评价的方面越多越能准确地反映用户的喜好。
| 表 1 第一组试验结果 Table 1 The first group experimental results |
| 表 2 第二组试验结果 Table 2 The second group experimental results |
| 表 3 第三组试验结果 Table 3 The third group experimental results |
表 3综合了三个方面评分的Icf_sip1方法, 在3个城市的旅游数据集的5个指标上均优于Icf_scenery、Icf_interest、Icf_price及Icf_global算法。Icf_sip2方法在桂林、杭州的旅游数据集的5个指标上均优于Icf_scenery、Icf_price、Icf_interest及Icf_global算法。在上海数据集上, Icf_sip2方法比Icf_sip1方法略差, 但两者差距极小。这说明利用用户对景点多个方面的评分信息也能有效改善物品间相似性的计算。分析其原因为:若两个物品在各方面得到不同用户的相似评价越多, 这两个物品就越有可能相似; 得到相似评价的方面越多, 物品相似的可能性也越大。但多方面评分的相似性更能体现用户间的相似性。
4 结语本研究提出基于多方面评分的景点协同推荐算法, 用以改进用户或景点间相似性的计算。从携程网上采集关于中国桂林、杭州、上海的景点信息, 设计了对比试验方案, 并通过均方根误差、平均绝对误差、覆盖率、准确率、F-度量指标来测评预测效果。试验结果表明, 相比于只利用单一的总体评分的推荐算法, 该算法使得用户及物品间的相似性计算更准确, 从而使评分预测更准确。未来可考虑通过综合利用更多的旅游数据, 如旅游图片、游记、用户评论以及地理位置信息等来更准确地计算用户或者物品间的相似性, 以进一步提高协同过滤的准确性。
| [1] |
乔向杰, 张凌云. 近十年国外旅游推荐系统的应用研究[J].
旅游学刊, 2014, 29 (8) : 117-127 QIAO Xiangjie, ZHANG Lingyun. Study on the application of foreign tourism recommendation system in recent ten years[J]. Tourism Tribune, 2014, 29 (8) : 117-127 |
| [2] | 文益民, 史一帆, 蔡国永, 等.个性化旅游推荐研究综述[EB/OL].[2014-07-03].http://www.paper.edu.cn/releasepaper/content/201407-56. |
| [3] |
史一帆, 文益民. 基于景点标签的协同过滤推荐[J].
计算机应用, 2014, 34 (10) : 2854-2858 SHI Yifan, WEN Yimin. Collaborative filtering recommendation based on tags of scenic spots[J]. Journal of Computer Applications, 2014, 34 (10) : 2854-2858 |
| [4] |
雷震, 文益民, 王志强, 等. 基于影响力控制的热传导算法[J].
智能系统学报, 2016, 11 (3) : 328-335 LEI Zhen, WEN Yimin, WANG Zhiqiang, et al. Heat conduction controlled by the influence of users and items[J]. CAAI Transactions on Intelligent Systems, 2016, 11 (3) : 328-335 |
| [5] |
庞俊涛, 张晖, 杨春明, 等. 基于概率矩阵分解的多指标协同过滤算法[J].
山东大学学报(工学版), 2016, 46 (3) : 65-73 PANG Juntao, ZHANG Hui, YANG Chunming, et al. Multi-criteria collaborative filtering algorithm based on probabilistic matrix factorization[J]. Journal of Shandong University (Engineering Science), 2016, 46 (3) : 65-73 |
| [6] | MAGID A, CHEN L, CHEN G, et al. A context-aware personalized travel recommendation system based on geotagged social media data mining[J]. International Journal of Geographical Information Science, 2013, 27 (4) : 662-684 DOI:10.1080/13658816.2012.696649 |
| [7] | GOLDBERG D, NICHOLS D, OKI B M, et al. Using collaborative filtering to weave an information tapestry[J]. Communications of the ACM, 1992, 35 (12) : 61-70 DOI:10.1145/138859.138867 |
| [8] | LINDEN G, SMITH B, YORK J. Amazon.com recommendations: item-to-item collaborative filtering[J]. IEEE Internet Computing[J]. IEEE Internet Computing, 2003, 7 (1) : 76-80 DOI:10.1109/MIC.2003.1167344 |
| [9] | DAS A S, DATAR M, GARG A, et al. Google news personalization: scalable online collaborative filtering[C]//Proceedings of the 16th International Conference on World Wide Web. New York, USA: ACM, 2007: 271-280. |
| [10] | BENNETT J, ELKAN C, LIU B, et al. KDD Cup and workshop 2007[J]. ACM SIGKDD Explorations Newsletter, 2007, 9 (2) : 51-52 DOI:10.1145/1345448 |
| [11] | RESNICK P, IACOVOU N, SUCHAK M, et al. GroupLens: an open architecture for collaborative filtering of netnews[C]// Proceedings of the 1994 ACM Conference on Computer Supported Cooperative Work. New York, USA: ACM, 1994: 175-186. |
| [12] | SARWAR B, KARYPIS G, KONSTAN J, et al. Item-based collaborative filtering recommendation algorithms[C]// Proceedings of the 10th International Conference on World Wide Web. Hong Kong, China: ACM, 2001: 285-295. |
| [13] | CHOI K, SUH Y. A new similarity function for selecting neighbors for each target item in collaborative filtering[J]. Knowledge-Based Systems, 2013, 37 (1) : 146-153 |
| [14] | LIU H F, HU Z, MIAN A, et al. A new user similarity model to improve the accuracy of collaborative filtering[J]. Knowledge-Based Systems, 2014, 56 (3) : 156-166 |
| [15] | ZHANG J, PENG Q, SUN S Q, et al. Collaborative filtering recommendation algorithm based on user preference derived from item domain features[J]. Physica A: Statistical Mechanics and its Applications, 2014, 396 (15) : 66-76 |
| [16] | YU X, WANG Z. A enhanced trust model based on social network and online behavior analysis for recommendation[C]// Proceedings of International Conference on Computational Intelligence and Software Engineering. Wuhan, China: IEEE, 2010: 1-4. |
| [17] | CHANG Q, WANG X K, YIN D, et al. The new similarity measure based on user preference models for collaborative filtering[C]// Proceedings of the 2015 IEEE International Conference on Information and Automation. Lijiang, China: IEEE, 2015: 557-582. |
| [18] |
文俊浩, 舒珊. 一种改进相似性度量的协同过滤推荐算法[J].
计算机科学, 2014, 41 (5) : 68-71 WEN Junhao, SHU Shan. Improved collaborative filtering recommendation algorithm of similarity measure[J]. Computer Science, 2014, 41 (5) : 68-71 |
| [19] | BREESE J S, HECKERMAN D, KADIE C. Empirical analysis of predictive algorithms for collaborative filtering[C]// Proceedings of the Fourteenth Conference on Uncertainty in Artificial Intelligence. Madison, USA: Morgan Kaufmann Publishers Inc, 1998: 43-52. |
| [20] | 项亮. 推荐系统实践[M]. 北京: 人民邮电出版社, 2012 . |
| [21] |
李聪, 梁昌勇, 马丽. 基于领域最近邻的协同过滤推荐算法[J].
计算机研究与发展, 2008, 45 (9) : 1532-1538 LI Cong, LIANG Changyong, MA Li. A collaborative filtering recommendation algorithm based on domain nearest neighbor[J]. Journal of Computer Research and Development, 2008, 45 (9) : 1532-1538 |




