2. 计算智能重庆市重点实验室, 重庆 400065
2. Chongqing Key Laboratory of Computational Intelligence, Chongqing 400065, China
时间序列预测方法是模拟时序数据的一种基本方法, 在现实生活的很多领域中都有着重大的意义。2007年, Taylor和Hinton等人观测到传统的受限玻尔兹曼机(restricted Boltzmann machine, RBM)模型可以高效的对数据分布式隐层概率进行推理[1-2], 于是在RBM模型基础上加入高斯思想和时序依赖条件, 提出基于高斯过程的条件受限玻尔兹曼机(Gaussian conditional RBM, GCRBM)时序模型, 该模型可以对带有高斯噪声的实值数据进行训练, 同时加入时序连接因子, 使得模型可以稳定的学习和生成大量的复杂时间序列数据。该模型继承了RBM优化目标似然函数时采用比度差异更新模型参数的规则[3-4], 让时序数据的学习和预测变得简单高效。
然而, 基于高斯过程的条件受限玻尔兹曼机时序模型只能对单一种类的时序数据进行很好的预测, 对多类时序数据的预测效果不是很好, 并且还难以训练真实的高维数据[1]。所以, 针对以上两个问题, 本研究提出基于集成深度学习的时间序列预测模型, 该模型集成了多个深网, 每一个深网都包含一个深可信网络模型(deep belief net, DBN)和GCRBM模型的组合。每一个深网首先通过DBN模型对每一类时序数据进行降维[5], 然后利用低维特征训练每一类数据的GCRBM时序模型。其中, DBN模型是深度学习的一个重要模型, 是HINTON G E等人于2006年提出来的一种非监督贪心逐层预训练加多层自动编码结构, 模型可以将原始高维数据映射至低维空间, 同时还含有相同的解码网络来恢复高维数据[6-8]。为了验证集成深度学习模型的可行性, 本研究采用中国科学院自动化研究所采集的CASIA-A步态数据集中16个人的步态序列进行了试验, 并结合相关方法(训练一个DBN网络对所有类别的时序数据降维, 然后利用RBF和支持向量机(support vector machine, SVM)对低维特征分类)进行比较, 试验结果验证了本研究方法的有效性和可行性。
1 相关技术简介本研究提出的模型中, 涉及到了两种基本模型, 首先用深可信网络模型对时序数据进行降维, 然后用基于GCRBM的时序模型对时序数据进行预测。
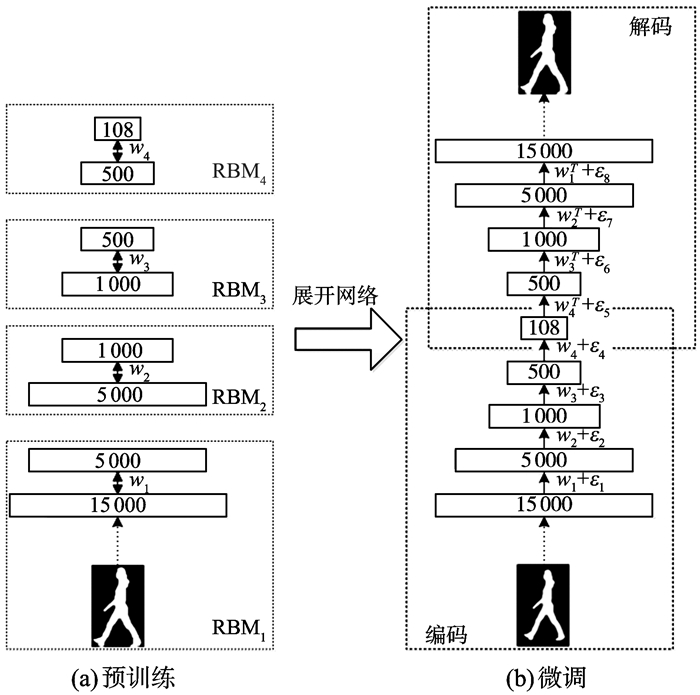
1.1 深可信网络模型深可信网络模型的总体结构包含两个过程:第一步是非监督贪心逐层RBM预训练; 第二步是多层反向传播神经网络(back propagation, BP)所构成的深层自动编码器(auto encoder, AE), 用于微调模型的权值。即模型首先通过多层RBM进行预训练, 然后将网络展开为编码学习和解码重构的双向自动编码器结构, 编码学习阶段将原始高维数据映射至低维空间, 解码重构阶段则通过相同的解码网络来重构数据[6-7]。深可信网络总体结构如图 1所示。
|
图 1 深可信网络工作结构 Figure 1 The working structure of deep belief network |
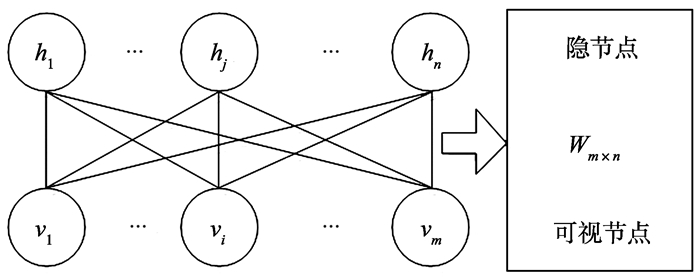
模型预训练所用到的RBM是含有随机二进制单元的两层网络, 分别是可视层和隐层, 两层之间带有对称的权值连接, 每层的节点之间无连接, 层和层节点间全连接[9-11], 其模型结构如图 2所示。
|
图 2 RBM基本结构 Figure 2 The basic structure of RBM |
RBM网络的输入层v和隐层h的能量函数
| $E\left( {v,h} \right) = - \sum\limits_i {{b_i}{v_i}} - \sum\limits_i {{c_j}{h_j}} - \sum\limits_i {{v_i}{h_j}{w_{ij}},} $ | (1) |
式中:vi和hj是可视层和隐层的网络节点值; bi和cj是可视层和隐层节点阈值; wij是连接两层之间权值。通过可视层输入, 得到隐层第j个节点的状态为有效值1的概率
| $p\left( {{h_j} = 1|v} \right) = f\left( {\sum\limits_{i = 1}^m {{w_{ij}}} \times {v_i} + {c_j}} \right),$ | (2) |
更新节点状态值是交替进行的, 即通过隐层节点值, 也可以得到可视层第i节点的状态为有效值1的概率
| $p\left( {{v_i} = 1|h} \right) = f\left( {\sum\limits_{j = 1}^n {{w_{ij}}} \times {h_j} + {b_i}} \right),$ | (3) |
网络的输出激励函数f(x)使用是sigmoid函数。RBM模型通过式(1)的整体能量函数E(v, h)为每一个可视层节点状态分配抽样概率
| $P\left( v \right) = \frac{{\sum\limits_h {{{\rm{e}}^{ - E\left( {v,h} \right)}}} }}{{\sum\limits_{v,h} {{{\rm{e}}^{ - E\left( {v,h} \right)}}} }},$ | (4) |
式中:分母表示一种配分函数形式[3], 代表基于所有可视层和隐层能量的节点活跃度; 分子代表基于所有隐层能量得到的可视层节点活跃度。一个系统中的能量越小, 则节点就越活跃。为了使可视层某一节点v的当前概率p(v)最大化, 则需要降低当前节点的能量, 并且同时提高其他节点的能量。通过对式(4)求对数操作logp(v)得到目标函数[3-4], 然后不断优化该目标函数, 并更新网络的权值和阈值参数(其中ε为模型学习率):
| ${w_{ij}} \leftarrow {w_{ij}} + \Delta {w_{ij}},\Delta {w_{ij}} = \varepsilon \frac{{\partial \log p\left( v \right)}}{{\partial {w_{ij}}}},$ | (5) |
| ${b_i} \leftarrow {b_i} + \Delta {b_i},\Delta {b_i} = \varepsilon \frac{{\partial \log p\left( v \right)}}{{\partial {b_i}}},$ | (6) |
| ${c_j} \leftarrow {c_j} + \Delta {c_j},\Delta {c_j} = \varepsilon \frac{{\partial \log p\left( v \right)}}{{\partial {c_j}}}.$ | (7) |
当模型预训练完成后, 将其展开为深层自动编码器双向网络结构, 编码初始权值使用RBM预训练好的权值信息, 然后执行BP学习算法微调参数[12], 在BP调整过程中不断降低原始数据和网络重构数据之间的重构误差[8]。通过向整个网络反向传播重构误差, 利用梯度下降算法调整网络权值和节点阈值, 直至满足最小误差要求。具体步骤为:
(1) 向前网络输出传播阶段
① 从样本集中选取样本和对应的标签信息(xp, yp), 将xp作为BP网络输入;
② 计算相应的网络实际输出op=fl(…(f2(f1(xpw1+θ1)w2+θ2)…)wl+θl), 其中: fl(x)是对第l层的sigmiod激励函数, wl是第l-1层和第l层之间节点间权值, θl是第l层隐层阈值信息。
(2) 向后的误差传播阶段
① 计算m个实际输出op与相应的理想输出yp的差值作为误差度量函数
| ${E_p} = \frac{1}{2}\sum\limits_{j = 1}^m {{{\left( {{y_{pj}} - {o_{pj}}} \right)}^2}} .$ | (8) |
② 通过整个网络向后方向传播误差, 传播过程中通过降低误差函数Ep的值来达到网络训练要求, 使用梯度下降算法进行网络权值修正
基于GCRBM时序模型也由两部分组成:第一部分是高斯的受限玻尔兹曼机(Gaussian RBM, GRBM)模型, 该模型的网络输出激励函数使用高斯函数N(x)代替sigmoid函数, 解决了RBM不能使用实型数据训练的问题; 第二部分是加条件的受限玻尔兹曼机(conditional RBM, CRBM), 该模型增加了两种直接连接时序信息的参数, 使得模型能够高效的预测时序数据。因此, CRBM模型在训练时序数据时会加上之前时刻的可视层数据作为固定输入, 通过结合前面几个时刻的时序过程来模拟一种时间依赖性[1-2]。
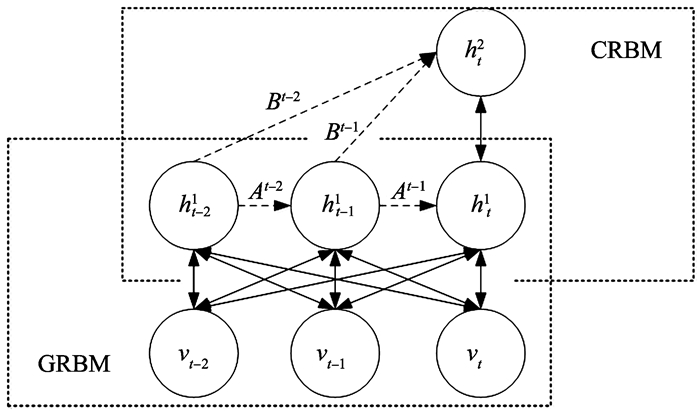
CRBM模型主要增加了两种类型的直连因子, 第一种因子A是从过去N个时间步的可视单元到当前时刻可视单元的配置参数; 第二种因子B是从过去M个时间步的可视单元到当前时刻隐层单元的配置参数。由于模型共含有3层网络, 前两层是GRBM结构, 所以GRBM的隐层可以看作是CRBM结构的可视层输入。图 3显示了结合3个时间步的时序模型结构图, 其中vi和hj是可视层和隐层的网络节点值, A和B是增加的两种直连因子。
|
图 3 GCRBM时序模型基本结构 Figure 3 The basic structure of GCRBM time series model |
CRBM训练过程中, 结合先前k个时刻的可视层数据作为动态变量, 实现直连的时间序列依赖性。所以在训练过程中某一时刻的可视层v和隐层h会加上之前k个时刻的可视层时序信息, 使得CRBM两层网络的阈值成为一种新的动态阈值bi, t和cj, t, 如下:
| ${b_{i,t}} = {b_i} + \sum\limits_k {{A_{ki}}{v_{k, < t}}} ,$ | (9) |
| ${c_{j,t}} = {c_j} + \sum\limits_k {{B_{ki}}{v_{k, < t}}} ,$ | (10) |
式中Aki和Bki表示模型的两种直连参数因子; bi和cj表示模型可视层和隐层节点静态阈值; vk, < t表示之前时间的可视层时序信息。结合模型权值和动态阈值, CRBM的能量函数[2]
| $\begin{array}{l} E\left( {{v_t},{h_t}|{v_{ < t}}} \right) = \frac{1}{2}\sum\limits_i {{{\left( {{v_{i,t}} - {b_{i,t}}} \right)}^2}} - \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{ij} {{w_{ij}}{v_{i,t}}{h_{j,t}} - \sum\limits_j {{c_{j,t}}{h_{j,t}}} ,} \end{array}$ | (11) |
式中: vi, t和hj, t为t时刻新的动态节点值。GCRBM模型更新权重和阈值的学习方法同RBM一致[3-4]。与一般RBM模型的不同之处在于:首先, GRBM网络的输出激励函数使用高斯函数N (x)代替sigmoid函数; 然后, CRBM在更新各层权值和阈值的同时, 还要更新两种直连因子A和B。以下为更新规则[2]:
| $\Delta A_{ki}^{\left( {t - q} \right)} = v_k^{t - q}\left( {\left\langle {v_i^t} \right\rangle - \left\langle {v_i^t} \right\rangle '} \right),$ | (12) |
| $\Delta B_{ij}^{\left( {t - q} \right)} = v_i^{t - q}\left( {\left\langle {h_j^t} \right\rangle - \left\langle {h_j^t} \right\rangle '} \right),$ | (13) |
式中, 〈vit〉和〈hjt〉为t时刻的网络节点值; 〈vit〉′和〈hjt〉′为t时刻的网络节点重构值[2]; vit-q为第t-1, t-2, …, t-q时刻的可视层节点值。
2 集成深度学习的时序预测模型基于GCRBM的时序模型可以稳定的预测时间序列[1-2], 但是该模型只能对单一种类的时序数据进行良好的预测, 对多类别的时序数据的预测效果并不是很好, 而且难以训练真实的高维数据。所以, 针对上述两个问题, 本研究提出基于集成深度学习的时间序列预测模型, 该模型集成了多个DBN模型和GCRBM模型的深网组合, 每一个深网首先通过DBN模型对每一类时序数据进行降维, 然后利用低维特征训练每一类数据的GCRBM时序模型。
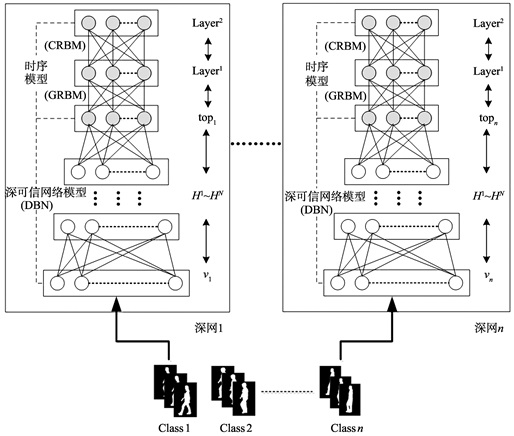
2.1 模型训练过程基于集成深度学习的时间序列预测模型总体结构如图 4所示, n个类别的步态时序数据分别训练n个深网结构, 每一个深网结构都由一个深可信网(DBN)和一个时序模型(GCRBM)组成。训练模型时, 每一类步态序列都要先通过DBN编码阶段学习低维特征, 低维特征再作为GCRBM模型的输入训练每一类步态序列相应的时序模型。每一个深网结构都会积累学习每一类别时序数据特征, 并更新网络参数。
|
图 4 集成深度学习模型总体结构 Figure 4 The overall structure of Integrated deep learning model |
模型的训练算法如下所示:
| 输入:n类时序数据V; DBN模型每层节点数Dl, l=1, …, k, DBN模型组的权值和阈值参数初始化wi/bi, i=1, …, n; GCRBM两层节点数layer1、layer2, GCRBM模型组的权值阈值和直接因子等参数初始化Xi/ci/Ai/Bi, i=1, …, n; 模型训练迭代次数e; RBM动量参数初始化θ; 神经网络学习率ε。 |
|
输出:网络模型参数Wi/bi、Xi/ci和Ai/Bi, i=1, …, n Step 1:训练一组深网模型 for m=1; m≤e do for i=1; i≤n do (1)通过式(5)~(7)的规则对多层RBM网络预训练并保存权值和阈值Wi/bi; (2)结合预训练参数, 根据1.1.2小节原理对模型进行微调, 保存权值阈值Wi/bi和低维特征topi; (3)利用低维特征topi训练时序模型, 结合公式(5)~(7)更新其权值阈值Xi/ci, 并结合式(12)(13)更新Ai/Bi因子。 end for end for Step 2:保存模型参数Wi/bi、Xi/ci和Ai/Bi, i=1, …, n |
给定一类时序数据的当前周期短序列, 其时序预测过程是:首先利用集成深网中DBN1~DBNn分别对数据学习低维特征, 并得到n个重构误差err1~errn, 通过重构误差计算样本最大重建概率, 识别出该时序在集成深网模型中对应类别的子网; 然后通过该子网中DBN编码学习获得时序低维特征, 利用该子网中GCRBM模型对低维特征预测后期时序的低维特征; 最后将预测出来的低维特征返回对应子网中的DBN解码重构出原始高维空间的时序数据。在DBN1~DBNn对数据样本x进行重建时, DBNi模型对x的重建概率
| $\begin{array}{l} P\left( {x'\left( t \right)|x} \right) = \frac{{\exp \left( { - {{\left\| {x'\left( i \right) - x} \right\|}^2}} \right)}}{{\sum\limits_i {\exp } \left( { - {{\left\| {x'\left( i \right) - x} \right\|}^2}} \right)}},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1 \ldots ,n. \end{array}$ | (14) |
从式(14)可知, 若DBNi对x的重建误差越小, 则所得到的重建概率最大, 即为正确识别x。通过找到DBN1~DBNn对x的最大重建概率P(x′(i)|x)来识别x类别, 识别规则
| $\begin{array}{l} C\left( x \right) = \arg \max \left\{ {P\left( {x'\left( i \right)|x} \right)} \right\},\\ \;\;\;\;\;\;\;\;\;\;\;i = 1, \ldots ,n, \end{array}$ | (15) |
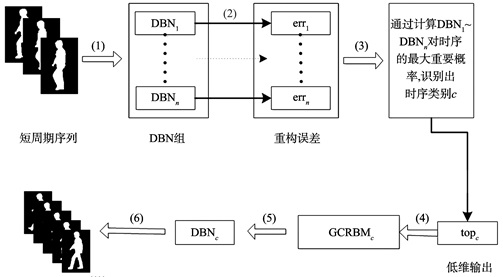
模型对时序的预测流程如图 5所示, 图中步骤可以简单描述为:(1) 对于一个新的步态短周期序列T, 遍历深可信网络组DBN1~DBNn; (2) 步态序列通过DBN1~DBNn得到重构误差err1~errn; (3) 通过n个重构误差err1~errn计算深网组对时序的最大重建概率, 识别出序列的类别c; (4) 利用相对应类别的DBNc的低维特征topc作为对应类别的时序模型GCRBMc输入来预测后期时序的低维特征; (5) 对模型预测的后期时序低维特征再通过对应类别的DBNc解码重构原始高维空间数据; (6) 将重构出的时序数据转换为步态图像序列。
|
图 5 集成深度学习模型时序预测流程 Figure 5 The time series predicting process of integrated deep learning model |
时序模型的预测算法为:
|
输入:某一类步态数据当前周期短序列T; 深网中n个子网模型参数Wi/bi、xi/ci和Ai/Bi, i=1, …, n; 模拟时序的目标帧数m。 |
| 输出:对当前周期短序列步态数据T的m帧时序预测数据 Step 1:识别步态序列类别, 并生成该类步态的后期时序预测数据 (1) 计算重构误差 for i=1; i≤n do 序列T经深网中DBNi模型, 得到重构数据与原数据的重构误差erri; end for (2) 通过式(14)(15)计算n组重构误差err1~errn和集成深网模型对时序的最大重建概率p, 识别出T的类别c; (3) 利用T的类别相对应的DBNc模型低维特征作为相对应类别时序模型GCRBMc的输入, 预测后期m帧时序低维特征g; Step 2:预测的时序低维特征g通过相对应的DBNc重构出原始空间数据g′。 |
为了验证模型对时间序列的预测性能, 本研究采用中国科学院自动化研究所采集的公开步态数据集CASIA-A进行了试验。该数据集一共含有20个人的行走步态数据, 本研究试验采用其中所有“00_1”和“00_3”数据, 即表示20个人的水平向左慢走和快走数据, 但是删除了其中3种序列特别少和1种效果特别差的序列。最终本研究方法一共使用了16个人的“水平向左步行”数据, 其中每一个人的步态序列对应一个类别, 每一类别序列数为120帧。试验对每一类别采用其前100帧作训练集, 后20帧作测试集, 并将每一帧步态图像经过剪切预处理, 其尺寸大小都统一为100*150, 图 6显示了预处理后的16类步态图像效果。

|
图 6 CASIA-A步态图像 Figure 6 The CASIA-A gait image |
集成深网络模型中每一个深网含有7层网络结构, 其中DBN网络含有5层网络(输入层、顶层输出和3个隐层), 时序模型含有3层网络。由于DBN的顶层输出作为时序模型的输入, 所以两种网络共用一层。在试验中, DBN向上学习采用“15 000-5 000-1 000-500-108”结构, 即输入层数据维度为15 000, 顶层输出维度为108, 中间三个隐层节点数分别为5 000、1 000和500。三层时序模型结构是“108-100-100”, 即输入层是DBN的输出层, 维度为108, 其第二层和第三层节点数均为100。由于试验数据一共有16类步态, 故集成模型需要训练16个结构为“15 000-5 000-1 000-500-108-100-100”的深网络。在RBM预训练阶段, 迭代次数为300次, BP神经网络微调次数为200次。训练时序模型时, 对其中GRBM和CRBM的训练迭代次数都是2 000次。
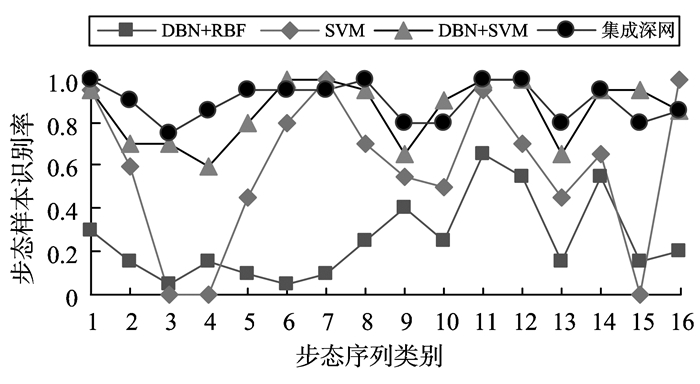
3.3 步态识别结果分析为了验证本研究方法的可行性, 通过试验比较了本研究方法与其余三种方法对同一个步态数据集的识别率[13-15]。第一种方法是先训练一个DBN网络对全部步态数据进行降维, 再用其低维特征使用径向基神经网络(radial basis function, RBF)进行分类; 第二种方法是直接使用支持向量机(support vector machine, SVM)分类器对原始步态数据进行分类; 第三种方法是先训练一个DBN网络对全部步态数据进行降维, 再用其低维特征使用SVM分类; 第四种是本研究提出的方法, 即集成深网络。试验数据中每一类步态测试数据含有20帧样本, 一共有16类, 图 7显示了几种方法对各类步态测试样本识别率情况。
|
图 7 几种方法的步态样本识别率对比结果 Figure 7 The contrastive result of several methods gait recognition rate |
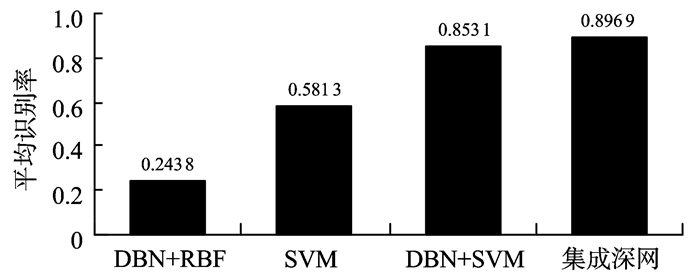
从图 7中可以看出, DBN+RBF和单独使用SVM这两种方法对于各个类别的步态样本识别效果比较紊乱, 其中几个类别样本识别率很高, 但大部分识别率较低。DBN+SVM和本研究方法效果都要优于前两者, 而本研究方法对各类步态样本识别率相比于DBN+SVM方法更好, 总体体现了本研究方法的优势。图 8则显示了各种方法对每一类步态全部样本的平均识别率, 从总体平均识别情况来看, 本研究方法同样优于其他几种方法。
|
图 8 几种方法的步态样本平均识别率对比情况 Figure 8 The contrastive result of several methods' average gait recognition rate |
为了整体把握模型对每一种步态序列的具体类别识别情况, 规定当某一类别的步态序列中识别样本数量达到一半以上, 则表示识别到该步态序列的类型。步态测试集每一类别都是20帧, 当其中某一类有11帧样本被识别正确, 则可以认为模型已经识别到该类步态序列, 然后通过时序模型模拟该类步态的后期时序数据。测试数据一共有16个步态序列类别, 几种方法对步态序列类别的识别数和识别率情况如表 1所示。
| 表 1 几种方法的步态序列类识别对比情况 Table 1 The contrastive result of several methods' classification of gait sequences |
由表 1可以看出:DBN+RBF方法对16类步态序列只能识别到5类, SVM能识别到11类, 而DBN+SVM以及本研究方法的效果依然优于前两者。本研究提出方法虽然对每一步态序列的样本不能达到全部识别, 但是都能很好地识别到11帧以上, 即本研究提出方法对步态序列的具体类别能够达到全部正确识别。
3.4 步态时序预测结果分析对于识别出来的序列, 根据对应类别的DBN模型的低维特征, 结合时序模型进行该步态的后期时序预测。预测效果相比于原图像有一些轻微噪声, 通过数字图像处理方法中的双峰值分割法加中值滤波对其进行去噪, 最后时序模型的模拟效果及其优化情况如图 9所示。试验结果表明:本研究提出模型可以对识别出的步态序列进行后期时序预测, 并能通过预测结果模拟出真实的步态序列。

|
图 9 时序模拟结果及其优化效果时序模拟结果及其优化效果时序模拟结果及其优化效果时序模拟结果及其优化效果 Figure 9 The simulated results and optimized effect of time series |
现对几种方法的时间复杂度进行客观分析。本研究提出的基于集成深度学习的时序模型训练过程一共迭代了e次, 且每一次迭代训练过程都要遍历n类步态时序数据, 所以本研究算法总体时间复杂度为O(ne); DBN+RBF方法训练一个DBN网络需要对全部步态数据进行降维, 再用其低维特征使用RBF进行分类, 其训练过程一共迭代了e次, 所以时间复杂度为O(e); SVM方法直接使用SVM分类器对全部步态数据进行一次性学习, 训练过程没有迭代, 其时间复杂度是O(1);第DBN+SVM方法先训练一个DBN网络对全部步态数据进行降维, 再用其低维特征使用SVM分类, 时间复杂度为O(e)。本研究提出方法的时间复杂度比其他比较方法高出n个数量级, 这是因为本研究方法集成了n个深网络导致的。但也正是因为集成了深度学习, 模型才体现了对n类步态的每一类别数据都能很好地学习其深层特征, 所以识别效果也优于其他几种方法。
4 结论本研究提出了一种集成深度学习的时间序列预测模型, 该模型集成多个深网结构, 每一个深网都通过DBN模型学习每一类时序数据低维特征, 并通过低维特征训练GCRBM时序模型。该模型的优点在于可以通过深可信网络组对目标数据进行降维并通过重建误差识别类别, 然后通过识别到的GCRBM模型预测目标数据的后期时序, 模型解决了基于高斯过程的条件受限玻尔兹曼机模型不能很好预测多类高维时序数据的问题。通过在中国科学院自动化研究所的CASIA-A步态数据集上进行试验, 试验结果表明本研究方法能够准确的识别出步态序列, 而且预测结果能够模拟出真实的步态序列, 这证实了本模型的有效性。下一步工作中, 将加入多种人体运动行为数据集, 继续进行试验和优化模型性能。
| [1] | TAYLOR G W, HINTON G E, ROWEIS S T. Modeling human motion using binary latent variables[C]// Advances in Neural Information Processing Systems (NIPS 19): Proceedings of the 2006 Conference.[S.l.]: MIT Press, 2007: 1345-1352. |
| [2] | TAYLOR G W, HINTON G E, ROWEIS S T. Two distributed-state models for generating high-dimensional time series[J]. Journal of Machine Learning Research, 2011, 12 (2) : 1025-1068 |
| [3] | HINTONG E. Training products of experts by minimizing contrastive divergence[J]. Neural Computation, 2006, 14 (8) : 1771-1800 |
| [4] | HINTON G E, OSINDERO S, WELLING M, et al. Unsupervised discovery of nonlinear structure using contrastive back propagation[J]. Cognitive Science, 2006, 30 (4) : 725-731 DOI:10.1207/s15516709cog0000_76 |
| [5] | ZENG Xianhua, LUO Siwei, WANG Jiao. Auto-associative neural network system for recognition[C]// Proceedings of International Conference on Machine Learning and Cybernetics (ICMLC 2007).[S.l.]: IEEE Conference Publications, 2007: 2885-2890. |
| [6] | HINTON G E, SALAKHUTDINOV R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313 (5786) : 504-507 DOI:10.1126/science.1127647 |
| [7] | HINTONG G E, SALAKHUTDINOV R. Supporting online material for reducing the dimensionality of data with neural networks[J]. Science, 2006, 504 (5786) : 504-507 |
| [8] | HINTONG G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18 (7) : 1527-1554 DOI:10.1162/neco.2006.18.7.1527 |
| [9] | SMOLENSKY P. Parallel distributed processing: information processing in dynamical systems: foundations of harmony theory[M]. Cambridge, USA: MIT Press, 1986 : 194 -281. |
| [10] | SALAKHUTDINOV R, JOSHUA B, TORRALBA A. Learning with hierarchical-deep models[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35 (8) : 1958-1971 |
| [11] | LAROCHELLE H, BEMGIO Y, LOURADOUR J, et al. Exploring strategies for training deep neural networks[J]. Journal of Machine Learning Research, 2009, 10 (6) : 1-40 |
| [12] |
孙志军, 薛磊, 许阳明. 深度学习研究综述[J].
计算机应用研究, 2012, 29 (8) : 2806-2810 SUN Zhijun, XUE Lei, XU Yangming. The research summary of deep learning[J]. Application Research of Computers, 2012, 29 (8) : 2806-2810 |
| [13] |
钟颖, 汪秉文. 基于遗传算法的BP神经网络时间序列预测模型[J].
系统工程与电子技术, 2002, 24 (4) : 9-11 ZHONG Ying, WANG Bingwen. The back propagation neural network based on genetic algorithm for predicting time series[J]. Journal of Systems Engineering and Electronics, 2002, 24 (4) : 9-11 |
| [14] |
张玉瑞, 陈剑波. 基于RBF神经网络的时间序列预测[J].
计算机工程与应用, 2005, 41 (11) : 74-76 ZHANG Yurui, CHEN Jianbo. A predicting time series model based on radial basis function neural network[J]. Computer Engineering and Applications, 2005, 41 (11) : 74-76 |
| [15] |
周若愚.基于SVR与半监督学习的时间序列预测[D].西安:西安电子科技大学, 2014.
ZHOU Ruoyu. A predicting time series model based on support vector regression and semi supervised learning[D]. Xi'an: Xidian University, 2014. http://cn.bing.com/academic/profile?id=763acf1875a7f97da4c8a63b23b7125b&encoded=0&v=paper_preview&mkt=zh-cn |




