2. 信息工程大学地理空间信息学院, 河南 郑州 450001
2. Institute of Geospatial Information, Information Engineering University, Zhengzhou 450001, Henan, China
为了保证我国基础地理信息的现势性, 国家测绘地理信息局2012年启动国家基础地理信息数据库动态更新工程, 至2014年已完成数据的三轮动态联动更新[1-2]。为避免大量数据的重复操作, 1:5万地形数据采用增量式更新方法, 在已有的数据基础上, 通过矢量空间数据实体间同名特征点匹配进行变化检测, 确定出需要更新的区域要素[3-5]。因此, 搜索的特征点需要位置准确、数量适中且分布合理, 为同名特征点匹配奠定基础。矢量数据匹配也是地理信息获取实时化、自动化等的关键技术[6-8]。
目前已有多种特征点的提取及匹配算法:提取算法中经典的算法有角度限制法、垂距限值法、Douglas-Peucker算法等。相比垂距限值法, Douglas-Peucker算法考虑了整条曲线, 但曲线起始点、限差的不确定对特征点精度影响较大, 曲线变形较大时一些局部变形特征点容易被遗漏[9-10]; 文献[11]提出的具有预测功能的矢量数据压缩算法, 虽然实现了较大数据压缩比, 但提取结果受起始点的影响较大, 需要找到最佳起始点; 文献[12]提出的基于最值点的Douglas-Peucker算法, 弥补了传统算法在图形复杂情况下出现的自相交, 但丢掉了局部变形的特征点; 文献[13]提出了一种基于斜率变化间接提取轮廓特征点的算法, 可以简化运算并减少噪声干扰, 但算法较繁杂; 文献[14]提出的改进矢量曲线特征点提取方法, 减少了计算量和数据冗余, 但会丢掉部分关键特征点。另外, 匹配的相似性度量指标有距离、形状、角度、方向和空间关系等[15-16]。文献[17]提出基于空间相似性的面实体匹配算法, 但该方法给出的形状中心点仅适合栅格图像, 具有一定局限性; 文献[18]提出基于拱高半径复变函数的面实体匹配算法, 有效地实现了同名实体的匹配, 但仅适用于面状要素的匹配; 文献[19]提出面质心结合多种匹配规则的匹配方法, 算法较复杂且只适用于面实体。文献[20]提出特征驱动下实体匹配指标自适应融合技术, 在一定程度上提高了匹配的智能性, 但也仅限面状要素的匹配。文献[21]和文献[22]分别用实体的重叠面积、比值及线实体的Frechet距离, 取得了较好的匹配效果。文献[23]和[24]对于面实体匹配较优, 但傅里叶变换方法较复杂。文献[25]利用方向关系进行实体匹配, 受限于方向关系的定量表达, 定性化比较困难。
鉴于已有算法的优点和局限性, 本研究结合矢量空间数据的坐标特征和方位角, 利用各个极值点斜率差的绝对值(以下简称斜率差值), 提出了一种分步提取特征点的算法和一种综合方位角与距离的同名特征点匹配算法, 经过试验验证分析, 本研究算法能同时适用于线状和面状矢量要素的特征点提取与匹配。
1 算法 1.1 特征点搜索算法本研究提出的特征点搜索算法采用分步提点的思想:首先提取实体要素在X、Y方向上的极值点; 其次在极值点中删除对曲线变化影响较小的冗余点; 最后对于一些变形较大但未能提取到特征点的曲线段添加合理特征点, 保留曲线局部特征。
1.1.1 提取极值点设S={pi=(xi, yi), i=1, 2, …, n}为地理实体要素轮廓点序列集合。提取X方向上极值点条件:
| $ {x_i} \ge {x_{i - 1}}{\rm{\& \& }}{x_i} > {x_{i + 1}}或{x_i} \le {x_{i - 1}}{\rm{\& \& }}{x_i}i + 1。 $ | (1) |
同理, 提取Y方向上极值点条件:
| $ {y_i} \ge {y_{i - 1}}{\rm{\& \& }}{y_i} > {y_{i + 1}}或{y_i} \le {y_{i - 1}}{\rm{\& \& }}{y_i}i + 1。 $ | (2) |
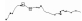
只要满足上述极值点提取公式的一种, 该点则被提取。图 1为提取结果示意图。

|
图 1 提取极值点结果示意图 Figure 1 The extraction result of extreme value point |
提取极值点作为初始特征点保留下来, 能避免直接搜索特征点时遗漏典型的特征点, 同时避免因阈值设置等因素导致提取的特征点不尽相同而造成特征点提取不稳定的弊端。
1.1.2 删除冗余极值点如图 1所示, pi与pi+6之间的极值点过于密集, 但对曲线的整体变形影响较小, 所以应删除这样的冗余极值点。
判断原则:设待判断极值点为pi, 其左右相邻极值点分别为pi-1、pi+1, 分别连接待判断极值点和左右相邻极值点, 可得两条连线斜率分别为kpipi-1、kpi+1pi, Δki为斜率差值, 则判断条件:
| $ \Delta {k_i} = |{k_{{p_i}{p_{i - 1}}}} - {k_{{p_{i + 1}}{p_i}}}| \le m,舍去; > m,保留。 $ | (3) |
其中:m为阈值, 阈值选取方法如表 1所示;
| $ {k_{{p_i}{p_{i - 1}}}} = {y_i} - {y_{i - 1}}{x_i} - {x_{i - 1}};{\rm{ }}{k_{{p_{i + 1}}{p_i}}} = {y_{i + 1}} - {y_i}{x_{i + 1}} - {x_i}. $ |
| 表 1 阈值选择 Table 1 Threshold selection |
添加合理特征点采用“查缺补漏, 因地制宜”的原则。首先以第二步保留的特征点为界将曲线分段, 在各段内按比例增加采样点, 然后对增加的采样点采用上述判断原则, 将采样点斜率差值按升序排列, 根据实际情况确定需要保留采样点的比率, 作为特征点。
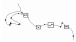
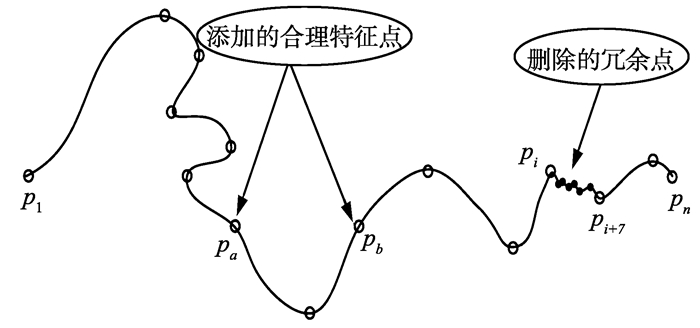
特征点提取结果如图 2所示, 其中点pa、pb表示添加的合理特征点, pi与pi+7之间表示删除冗余点的结果。
|
图 2 添加合理特征点 Figure 2 Add the reasonable feature points |
本研究提出结合距离和方位角的相似度匹配算法, 将这两个条件所判别的特征点相似程度归结为相似度, 来衡量特征点是否为同名特征点, 从而提高特征点匹配的精度。匹配步骤如下:
(1) 选取控制点
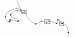
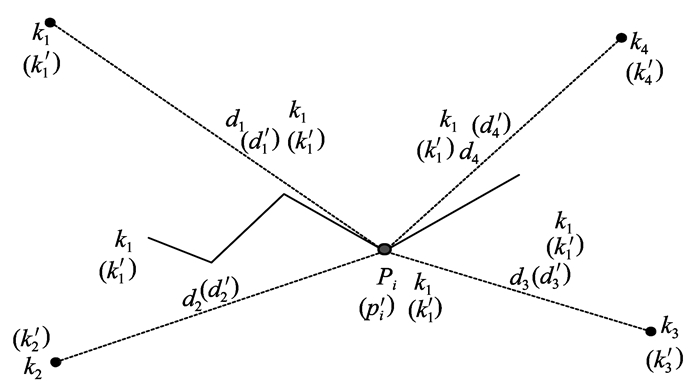
在进行匹配的两幅矢量图上选取相对应的四对控制点k1和k′1、k2和k′2、k3和k′3、k4和k′4, 保证控制点合理的分布在数据的四个方位, 以便有效的控制全部特征点数据。特征点与各控制点距离示意图如图 3所示。
|
图 3 特征点与各控制点距离示意图 Figure 3 The distance of feature point and control points |
(2) 计算距离平均差值
将特征点分别与控制点相连, 待匹配特征点pi和四个控制点的距离为d1、d2、d3和d4, 候选特征点p′i与四个控制点的距离为d′1、d′2、d′3、d′4, 如图 3所示。分别计算两幅矢量图上特征点与控制点距离之和, 并作差取平均, 计算平均距离差值
| $ {D_{{\rm{mean}}}} = \frac{{({d_1} + {d_2} + {d_3} + {d_4}) - (d{\prime _1} + d{\prime _2} + d{\prime _3} + d{\prime _4})}}{4}。 $ | (4) |
(3) 计算夹角
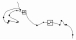
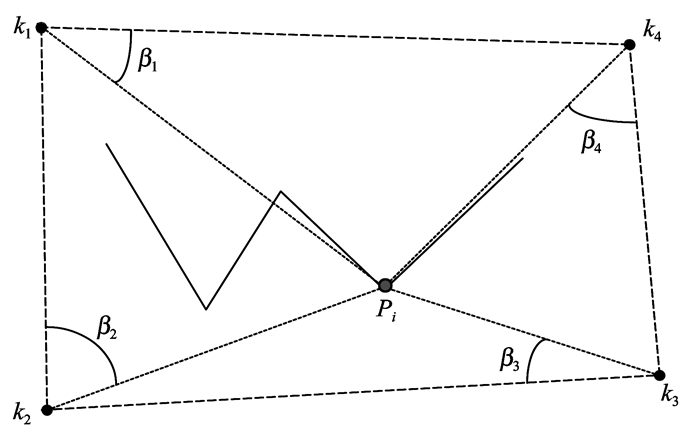
在进行夹角计算时, 为了保证不受坐标系的影响, 不能使用方位角, 夹角为控制点与特征点的连线和控制点与其顺时针相邻控制点连线之间的角度。在计算夹角时, 要保证夹角对应位置的准确性。角度计算示意图如图 4所示。
|
图 4 角度计算示意图 Figure 4 The angle calculation |
夹角β计算公式如下:
| $ \beta = {\alpha _1} - {\alpha _2}。 $ | (5) |
式中: α1表示对应的控制点ki(i=1, 2, 3, 4)与特征点pi连接的边的方位角; α2表示对应的控制点ki(i=1, 2, 3, 4)与其顺时针相邻控制点连接的边的方位角。当β > π时, β=2π-β。夹角计算示意图如图 5所示。

|
图 5 夹角计算示意图 Figure 5 The included angle calculation |
(4) 计算角度平均差值
两幅矢量空间数据上同名特征点所对应的四个夹角进行对比, 并求其差值, 将所得四个差值求平均, 得到角度平均差值
| $ {A_{{\rm{mean}}}} = \frac{{({\beta _1} + {\beta _2} + {\beta _3} + {\beta _4}) - \left( {\beta {\prime _1} + \beta {\prime _2} + \beta {\prime _3} + \beta {\prime _4}} \right)}}{4}。 $ | (6) |
(5) 计算相似度
计算两幅矢量空间数据上任意特征点之间的相似度S, 若S大于给定阈值T, 则对应两点为同名特征点。S计算公式如下:
| $ S = 1 - \frac{{{D_{{\rm{mean}}}}}}{{{d_{{\rm{max}}}}}} - \frac{{{A_{{\rm{mean}}}}}}{{{a_{{\rm{max}}}}}}。 $ | (7) |
其中:dmax=max{d1, d2, d3, d4, d′1, d′2, d′3, d′4}; amax=max{β1, β2, β3, β4, β′1, β′2, β′3, β′4}。
由此可以看出, 相似度S越大, 则表示两个点的相似程度越高。当存在多个点匹配时, 取相似度最大的一对点作为同名特征点。
2 试验与分析试验主要是对相同坐标系下不同比例尺的线实体和相同坐标系下不同时相的面实体进行同名特征点匹配, 验证本研究所提算法对同名特征点提取与匹配的效果。
2.1 相同坐标系下不同比例尺的线实体同名特征点匹配 2.1.1 试验数据试验所采用的数据来自国家基础地理信息系统数据库中的全国1:1 000万铁路矢量数据和全国1:1 500万铁路矢量数据中的部分数据(简称试验数据一)。试验数据如图 6所示。

|
图 6 试验数据一 Figure 6 The experimental data 1 |
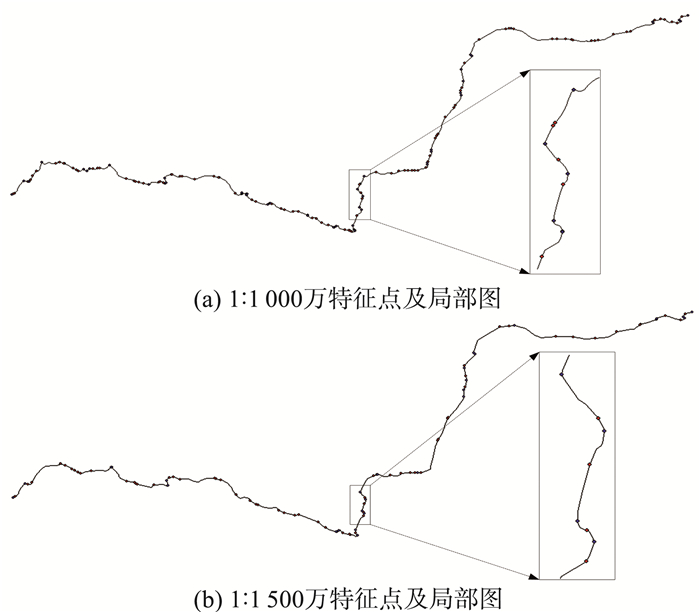
线实体的极值点一般是进行特征点匹配的主要对象。利用本研究所提出的特征点搜索算法, 提取的特征点及局部放大图如图 7所示, 其中蓝色圆点表示第二步保留的特征点, 红色圆点表示第三步添加的合理特征点。经过反复试验, 删除冗余极值点阈值m=tan 125°。补充合理特征点, 采样点所取比率为20%, 采样点斜率差值排序后, 所取比率为20%。
|
图 7 试验数据一特征点提取及局部图 Figure 7 The feature points of the experimental data 1 and local map |
由于1:1 000万的线实体与1:1 500万的线实体处在同一坐标系下, 两幅矢量数据上选取的控制点坐标相同, 控制点坐标如表 2所示。
| 表 2 试验数据一所选控制点 Table 2 The control points of the experimental data 1 |
在特征点提取和控制点确定的基础上, 利用Matlab实现特征点的匹配。经过反复试验, 相似度阈值取为0.996。对相似度匹配结果进行整理, 可得匹配情况如表 3所示。
| 表 3 线实体相似度匹配结果 Table 3 The matching results of linear entity similarity |
表 3表明, 当T=0.996时, 匹配成功点为51个, 其中4个特征点匹配重复, 匹配正确率为92.15%。
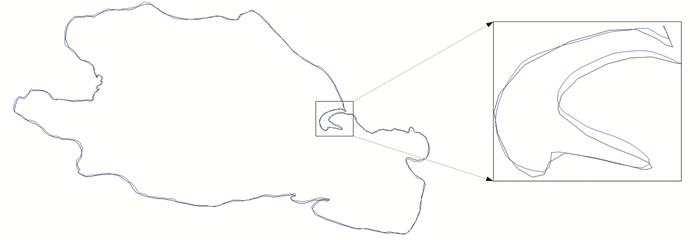
2.2 相同坐标系下不同时相的面实体同名特征点匹配 2.2.1 试验数据图 8为面实体试验所采用的不同时相青海湖边界矢量数据(简称试验数据二)。其中蓝色边界为2000年数据, 灰色边界为2008年数据。
|
图 8 试验数据二边界叠加及局部图 Figure 8 The boundary superposition of the experimental data 2 and local map |
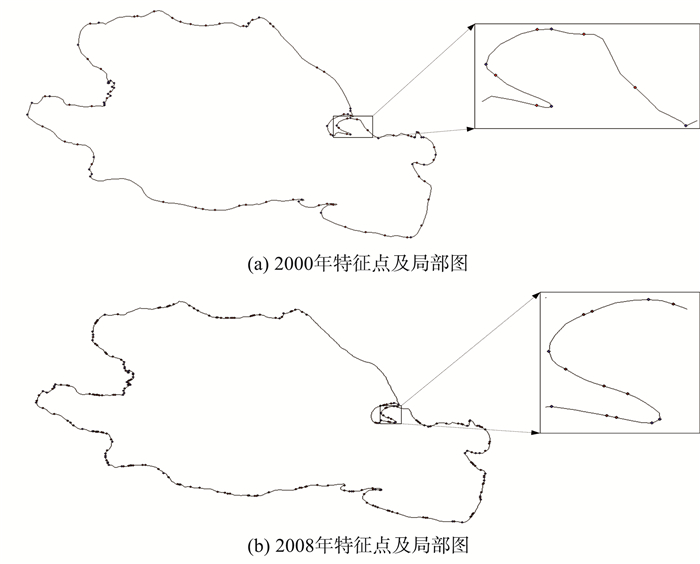
面实体特征点提取与线实体特征点提取方法类似, 面实体特征点提取结果如图 9所示。
|
图 9 试验数据二特征点提取及局部图 Figure 9 The feature points of the experimental data 2 and local map |
试验数据二所选取的控制点如表 4所示。
| 表 4 试验数据二所选控制点 Table 4 The control points of the experimental data 2 |
经过反复试验相似度阈值取为0.965。对相似度匹配结果进行整理, 可得匹配情况如表 5所示。试验结果表明, 当相似度阈值sim0=0.965时, 匹配成功点数r=61, 其中17个特征点匹配重复, 匹配正确率P=72.13%。表 5中n为匹配中所用的特征点数。由于本试验所采用的是相同坐标系不同时相青海湖矢量数据, 青海湖边界发生了一定变化, 所以匹配正确率相对较低, 与实际情况相符。
| 表 5 匹配试验结果 Table 5 The matching results |
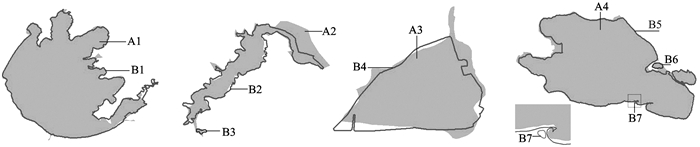
试验选取中国两个不同年份(2008年和2015年)水系数据, 选取如图 10所示4组算例:(a) A1和B1, (b) A2和B2、B3, (c) A3和B4, (d) A4和B5、B6、B7。文献[11]中算法综合利用待匹配实体形心、边界点、面积等属性来描述实体间的相似度, 文献[15]通过计算两实体的重叠面积来描述实体间的相似度。采用查准率和查全率作为性能评估指标, 与文献[11]和文献[15]进行试验对比分析。试验结果如表 6~8所示。
|
图 10 匹配试验所用实体对 Figure 10 The entities of the experimental |
| 表 6 本研究算法匹配结果 Table 6 The matching results of this research |
| 表 8 本研究算法与文献[11]、[15]算法比较 Table 8 Results of comparison with matching methodsin the references [11] and [15] |
文献[11]算法相似度模型虽然简单易实现, 匹配速度快, 但是匹配中要求两形状边界节点和实体形心相对位置一致, 故节点坐标对匹配精度影响较大。文献[15]利用重叠面积进行相似度计算, 但如图 10和表 7所示, 当A4和B7并不存在重叠面积时, 将不能识别两者的匹配度。本研究算法避免文献[15]中出现的弊端, 利用距离和斜率差进行特征点的搜索, 避免了文献[11]中边界节点和实体形心相对位置的影响, 匹配结果正确率较高, 算法有效。
3 结语本研究分析了当前同名特征点搜索与匹配算法的优劣, 并在此基础上提出了基于斜率差值和方位角的同名特征点搜索和匹配算法, 并分别对同一坐标系下不同比例尺的线实体以及同一坐标系下不同时相面实体进行试验, 试验结果分析验证了本研究所提出的方法是合理可行的。但算法还存在一定的不足, 如在计算相似度时, 出现了重复匹配的现象, 在后续的研究中将考虑如何减少重复匹配(如增加语义条件等), 提高匹配精度。
| [1] |
王东华, 刘建军. 国家基础地理信息数据库动态更新总体技术[J].
测绘学报, 2015, 44 (7) : 822-825 WANG Donghua, LIU Jianjun. Key techniques for dynamic updating of national fundamental geographic information database[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44 (7) : 822-825 |
| [2] |
刘建军, 吴晨琛, 杨眉, 等. 对基础地理信息应需及时更新的思考[J].
地理信息世界, 2016, 23 (2) : 79-82 LIU Jianjun, WU Chenchen, YANG Mei, et al. Thoughts of demand-response real-time updating of fundamental geographic information[J]. Geomatics World, 2016, 23 (2) : 79-82 |
| [3] |
王东华, 刘建军, 商瑶玲, 等. 国家1: 50 000基础地理信息数据库动态更新[J].
测绘通报, 2013, 7 : 1-4 WANG Donghua, LIU Jianjun, SHANG Yaoling, et al. Dynamic updating of national fundamental geography information database[J]. Bulletin of Surveying and Mapping, 2013, 7 : 1-4 |
| [4] |
刘建军. 国家基础地理信息数据库建设与更新[J].
测绘通报, 2015, 10 : 1-3 LIU Jianjun. Construction and updating of national fundamental geographic information database[J]. Bulletin of Surveying and Mapping, 2015, 10 : 1-3 |
| [5] |
张元杰, 刘建军, 刘剑炜, 等. 要素级多时态地形数据库建库与管理技术设计[J].
地理信息世界, 2014, 21 (1) : 29-32 ZHANG Yuanjie, LIU Jianjun, LIU Jianwei, et al. Building feature based multi spatio-temporal topographic database management system[J]. Geomatics World, 2014, 21 (1) : 29-32 |
| [6] |
付仲良, 周凡, 逯跃锋. 基于GIS技术的电网应急态势标绘[J].
山东大学学报(工学版), 2013, 43 (4) : 1-6 FU Zhongliang, ZHOU Fan, LU Yuefeng. Power grid emergency situation plotting technology based on GIS[J]. Journal of Shandong University (Engineering Science), 2013, 43 (4) : 1-6 |
| [7] |
郑君君, 夏胜平, 李新光, 等. 基于RSOM树的图像K近邻求解算法[J].
山东大学学报(工学版), 2011, 41 (2) : 80-84 ZHENG Junjun, XIA Shengping, LI Xinguang, et al. Knearest neighbors detecting algorithm based on a RSOM tree[J]. Journal of Shandong University (Engineering Science), 2011, 41 (2) : 80-84 |
| [8] |
许靖, 蔡文学, 黄晓宇. 基于经验修正策略的延时地图匹配算法[J].
山东大学学报(工学版), 2011, 41 (5) : 69-75 XU Jing, CAI Wenxue, HUANG Xiaoyu. An empirical correction strategy based delays map-matching algorithm[J]. Journal of Shandong University (Engineering Science), 2011, 41 (5) : 69-75 |
| [9] | MCMASTER R B. The integration of simplification and smoothing algorithms in line generalization[J]. Cartographica, 1989, 26 (1) : 101-121 DOI:10.3138/C213-3627-90X7-LR15 |
| [10] |
牛玉礼, 李岁劳, 任鸿飞, 等. 一种基于曲率分析的电子地图数据压缩方法[J].
机械与电子, 2013 (7) : 23-26 NIU Yuli, LI Suilao, REN Hongfei, et al. A new method of electronic map data compression based on the curvature analysis[J]. Machinery & Electronics, 2013 (7) : 23-26 |
| [11] |
黄培之. 具有预测功能的曲线矢量数据压缩方法[J].
测绘学报, 1995, 24 (4) : 316-319 HUANG Peizhi. Vector data compression with prediction function[J]. Acta Geodaetica et Cartographica Sinica, 1995, 24 (4) : 316-319 |
| [12] |
赵永清, 谢传节, 乔玉良, 等. 基于最值点的道格拉斯普克压缩算法[J].
软件导刊, 2008, 11 (7) : 60-62 ZHAO Yongqing, XIE Chuanjie, QIAO Yuliang, et al. Douglas-peucker compressing algorithm about extreme points[J]. Software Guide, 2008, 11 (7) : 60-62 |
| [13] |
王海晓, 朱旭光. 一种基于斜率变化间接提取轮廓特征点的算法[J].
软件导刊, 2010, 11 (9) : 66-67 WANG Haixiao, ZHU Xuguang. An algorithm of extracting contour feature points based on slope variation[J]. Software Guide, 2010, 11 (9) : 66-67 |
| [14] |
喜文飞, 方源敏, 隋玉成, 等. 一种改进的矢量曲线特征点提取方法[J].
江西科学, 2011, 29 (2) : 282-284 XI Wenfei, FANG Yuanmin, SUI Yucheng, et al. An improved feature extraction method of vector curves[J]. Jiangxi Science, 2011, 29 (2) : 282-284 |
| [15] |
徐枫, 邓敏, 赵彬彬, 等. 空间目标匹配方法的应用分析[J].
地球信息科学学报, 2009, 11 (5) : 657-663 XU Feng, DENG Min, ZHAO Binbin, et al. A detailed investigation on the methods of object matching[J]. Journal of Geo-Information Science, 2009, 11 (5) : 657-663 DOI:10.3724/SP.J.1047.2009.00657 |
| [16] |
孟妮娜.尺度变换中空间关系相似性的计算与评价[D].武汉:武汉大学, 2011.
MENG Nina. Calculation and evaluation of spatial relations similarity degree in cartographic generalization[D].Wuhan: Wuhan University, 2011. http://cn.bing.com/academic/profile?id=020f7a0a803302febb5ead1550a886b7&encoded=0&v=paper_preview&mkt=zh-cn |
| [17] |
郝燕玲, 唐文静, 赵玉新, 等. 基于空间相似性的面实体匹配算法研究[J].
测绘学报, 2008, 37 (4) : 501-506 HAO Yanling, TANG Wenjing, ZHAO Yuxin, et al. Areal feature matching algorithm based on spatial similarity[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37 (4) : 501-506 |
| [18] |
付仲良, 逯跃锋. 一种基于拱高半径复变函数的面实体匹配算法[J].
计算机应用研究, 2012, 29 (9) : 3303-3306 FU Zhongliang, LU Yuefeng. Polygon entity matching algorithm based on arc-height radius complex function[J]. Application Research of Computers, 2012, 29 (9) : 3303-3306 |
| [19] | YUAN S, TAO C. Development of conflation components[C]//Proceedings of Geoinformatics 1999 Conference. Ann Arbor, USA: University of Michigan, 1999:1-13. |
| [20] |
叶亚琴, 陈波, 万波, 等. 特征驱动下区实体匹配指标自适应融合技术[J].
测绘科学, 2012, 37 (6) : 101-103 YE Yaqin, CHEN Bo, WAN Bo, et al. Adaptive fusion technology of match indicators on area entity driven by data characteristics[J]. Science of Surveying and Mapping, 2012, 37 (6) : 101-103 |
| [21] |
吴建华, 付仲良. 数据更新中要素变化检测与匹配方法[J].
计算机应用, 2008, 28 (6) : 1612-1615 WU Jianhua, FU Zhongliang. Methodology of feature change detection and matching in data updating[J]. Journal of Computer Applications, 2008, 28 (6) : 1612-1615 DOI:10.3724/SP.J.1087.2008.01612 |
| [22] |
安晓亚, 刘平芝, 杨云, 等. 一种线状要素几何相似性度量方法及其应用[J].
武汉大学学报:信息科学版, 2015, 40 (9) : 1225-1229 AN Xiaoya, LIU Pingzhi, YANG Yun, et al. A geometric similarity measurement method and applications to linear feature[J]. Geomatics and Information Science of Wuhan University, 2015, 40 (9) : 1225-1229 |
| [23] |
黄智深, 钱海忠, 郭敏, 等. 面状居民地匹配骨架线傅里叶变化方法[J].
测绘学报, 2013, 42 (6) : 913-921 HUANG Zhishen, QIAN Haizhong, GUO Min, et al. Matching algorithm of polygon habitations based on their skeleton-lines using Fourier transform[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42 (6) : 913-921 |
| [24] |
陈占龙, 覃梦娇, 吴亮, 等. 利用多级弦长弯曲度复函数构建复杂面实体综合形状相似度量模型[J].
测绘学报, 2016, 45 (2) : 224-232 CHEN Zhanlong, QIN Mengjiao, WU Liang, et al. Establishment of the comprehensive shape similarity model for complex polygon entity by using bending multilevel chord complex function[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45 (2) : 224-232 |
| [25] |
陈占龙, 周林, 龚希, 等. 基于方向关系矩阵的空间方向相似性定量计算方法[J].
测绘学报, 2015, 44 (7) : 813-821 CHEN Zhanlong, ZHOU Lin, GONG Xi, et al. A quantitative calculation method of spatial direction similarity based on direction relation matrix[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44 (7) : 813-821 |