基于MapReduce模型的分布式粒子群算法

引用本文

范德斌, 邓长寿, 袁斯昊, 谭旭杰, 董小刚. 基于MapReduce模型的分布式粒子群算法[J]. 山东大学学报(工学版), 2016, 46(6): 23-30. DOI: 10.6040/j.issn.1672-3961.1.2016.161. 复制到剪切板

FAN Debin, DENG Changshou, YUAN Sihao, TAN Xujie, DONG Xiaogang. Distributed particle swarm optimization algorithm based on mapreduce[J]. Journal of Shandong University (Engineering Science), 2016, 46(6): 23-30. DOI: 10.6040/j.issn.1672-3961.1.2016.161. 复制到剪切板

基金项目

国家自然科学基金资助项目(61364025);武汉大学软件工程国家重点实验室开放基金资助项目(SKLSE2012-09-39);江西省教育厅科学技术资助项目(GJJ13729, GJJ14742)

作者简介

范德斌(1981-), 男, 江西赣州人, 副教授, 硕士, 主要研究方向为计算智能.E-mail:fandebin@126.com

通讯作者

邓长寿(1972-), 男, 安徽肥西人, 教授, 博士(后), 主要研究方向为计算智能.E-mail:csdeng@jju.edu.cn

文章历史

收稿日期：2015-12-30
网络出版时间：2016-09-22 08:55:10

Contents Abstract Full text Figures/Tables PDF

基于MapReduce模型的分布式粒子群算法

范德斌, 邓长寿, 袁斯昊, 谭旭杰, 董小刚

九江学院信息科学与技术学院, 江西九江 332005

收稿日期：2015-12-30 ；网络出版时间：2016-09-22 08:55:10

基金项目：国家自然科学基金资助项目(61364025);武汉大学软件工程国家重点实验室开放基金资助项目(SKLSE2012-09-39);江西省教育厅科学技术资助项目(GJJ13729, GJJ14742)

作者简介：范德斌(1981-), 男, 江西赣州人, 副教授, 硕士, 主要研究方向为计算智能.E-mail:fandebin@126.com

通讯作者：邓长寿(1972-), 男, 安徽肥西人, 教授, 博士(后), 主要研究方向为计算智能.E-mail:csdeng@jju.edu.cn

摘要：通过对传统的单种群粒子群算法的分析, 提出一种基于MapReduce模型的分布式粒子群算法, 解决粒子群算法在求解大规模优化问题时求解效率和精度明显下降等问题。在粒子群进化过程中, 粒子速度和位置的更新采用惯性权重的方法, 其权重值线性递减, 并且利用多子群进化策略, 提高算法的收敛精度。通过MapReduce模型实现算法的并行化, 有效提高算法求解效率。选取目前比较流行的几种算法, 并在13个500维、1 000维的标准测试函数上仿真试验, 结果显示该算法具有良好的优化性能。

关键词: 粒子群并行大规模优化分布式 MapReduce模型

Distributed particle swarm optimization algorithm based on mapreduce

FAN Debin, DENG Changshou, YUAN Sihao, TAN Xujie, DONG Xiaogang

School of Information and Technology, Jiujiang University, Jiujiang 332005, Jiangxi, China

Abstract: A distributed particle swarm optimization algorithm based on MapReduce was proposed through the analysis of the traditional single population particle swarm optimization algorithm, which was used to solve the algorithm problems of decreased efficiency and accuracy in large scale optimization. In the evolutionary process of particle swarm algorithm, the particle's velocity and position was updated by using the method of inertia weight, its value was decreased linearly, the accuracy of convergence was improved by adopting the strategies of multi population evolution. The process of the algorithm was parallel through the MapReduce model, which could improve the efficiency of the algorithm effectively. Several popular algorithms were selected and tested on 13 benchmark functions of 500 dimensions and 1 000 dimensions. The results showed that the algorithm has good optimization performance.

Key words: particle swarm optimization parallel large scale optimization distributed MapReduce model

0 引言

粒子群优化算法(particle swarm optimization, PSO)是模拟鸟类扑食行为的群体智能算法^[1], 由KENNDY J等人于1995年提出。PSO算法简单、需要调整的参数少, 具有较高的收敛速度、鲁棒性等特点, 广泛应用于函数优化^[2]、模糊系统控制^[3]、神经网络训练^[4]以及其他遗传算法^[5-6]的应用领域等, 且已取得较好的效果。算法在解决低维函数优化问题时表现出出色的性能, 然而随着维数和群体规模的增大, 传统的单机模式在求解问题时所需的时间和空间代价巨大, 算法存在收敛速度下降、求解精度不高、甚至无法找到问题的最优解等缺陷^[7]。即使通过增加硬件资源, 也无法满足人们的需求。近年来兴起的用于处理大数据的MapReduce模型^[8-9], 具有并行计算、分布式计算等特点, 是解决此类问题的一种可行、可靠的途径之一。目前关于粒子群算法结合MapReduce实现的研究有一些成果, 例如文献[10]介绍了基本的粒子群算法在MapReduce模型下的一种实现方式^[10]; 文献[11]提出基于粒子群算法的k-means算法在MapReduce上的实现^[11]; 文献[12]利用MapReduce模型设计并实现了粒子群投影寻踪算法的并行化, 取得不错的加速性能。而针对大规模优化问题的研究尚未深入。本研究旨在将粒子群算法与MapReduce模型结合, 提出一种基于MapReduce模型的分布式粒子群优化算法(distributed Particle swarm optimization based on MapReduce, DPSO-MR)。DPSO-MR采用惯性权重线性递减权值策略, 并结合多子群进化策略, 从而提高算法的收敛速率, 解决求解大规模优化问题时所需的时间和空间代价过高的问题。

1 基本概念 1.1 基本粒子群算法

粒子群算法中每个鸟就是PSO算法中的1个粒子, 代表D维搜索空间中的1个点, 设群体由N个粒子组成, 每个粒子都有1个当前位置和飞行速度:

$ {X_i} = \left[ {{x_{i1}},{x_{i2}}, \ldots ,{x_{id}}} \right], $

(1)

$ {V_i} = \left[ {{v_{i1}},{v_{i2}}, \ldots ,{v_{id}}} \right], $

(2)

其中:i=1, 2, …, N, 每个粒子在搜索空间中飞行, 通过迭代找到最优解。P_i=[p_i1,p_i2,…, p_id]为粒子的个体最优解, P_g=[p_g1,p_g2,…, p_gd]为种群中所有粒子的全局最优解。

在每次迭代中, 粒子的速度和位置根据式(3)、式(4)所示的形式进行更新:

$ \begin{array}{l} {v_{id}}\left( {k + 1} \right) = w{v_{id}}\left( k \right) + {c_1}{r_1}\left( {{p_{id}}\left( k \right) - {x_{id}}\left( k \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{c_2}{r_2}\left( {{p_{gd}} - {x_{id}}\left( k \right)} \right), \end{array} $

(3)

$ {x_{id}}\left( {k + 1} \right) = {x_{id}}\left( k \right) + {v_{id}}\left( {k + 1} \right), $

(4)

式中:k是迭代次数; r₁和r₂是[0, 1]之间的随机数, 这两个参数对群体的多样性起作用; c₁和c₂是加速因子, 使粒子具有自我总结和向群体中优秀个体学习的能力, 从而向粒子个体最优解以及群体全局最优解靠近, 在迭代过程中, 适当调整这两个参数, 可以减少局部收敛的困扰, 当然也会使收敛速度加快; w是惯性权重, 影响粒子的探索能力和开发能力^[13]。在基本粒子群算法中, 粒子采用相同的搜索策略, 粒子的多样性大大下降。

1.2 MapReduce介绍

MapReduce是一个流行的针对数据密集任务的分布式计算模型, 它的概念和思想主要来自矢量编程语言和函数式编程语言, 极大地方便编程人员在不会分布式并行编程的情况下, 将自己的程序部署在分布式系统上^[14]。

MapReduce模型简单易懂, 将复杂的并行计算过程高度地抽象成为2个函数, 即Map和Reduce。其中, Map函数负责对整个任务进行分解, 而Reduce函数负责把分解后的多任务处理结果进行规约汇总。Map函数接收1组数据并将其转换为1个key-value对列表, 输入域中每个元素对应1个key-value对。Reduce函数接收Map函数生成的列表, 然后根据它们的key值缩小key-value对列表, 同时作为最终的结果写入分布式文件系统(hadoop distributed file system, HDFS)。

MapReduce的具体工作流程见图 1。

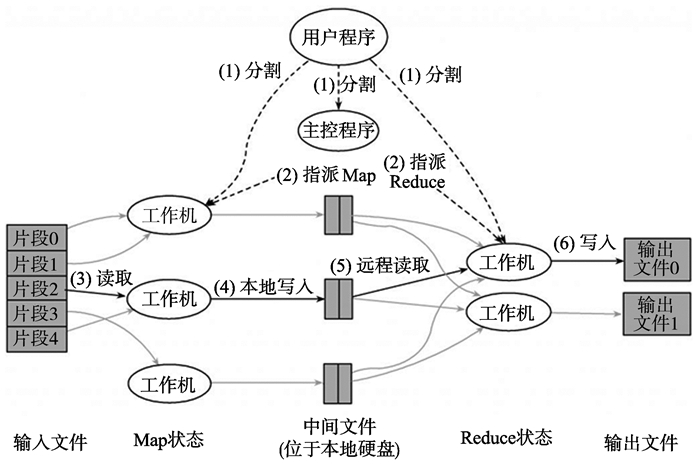
图 1 MapReduce工作流程 Figure 1 Work flow of MapReduce

2 基于MapReduce模型的分布式粒子群算法 2.1 线性递减权值策略

文献[15]于1998年首次提出惯性权重的概念, 通过研究发现惯性权重可以很好地控制粒子的搜索范围, 惯性权重选取的好坏直接影响到算法性能和效率。

目前粒子群算法中惯性权重的确定从依赖经验到各种策略的初探取得了一定的成效。由于惯性权重的选择仍旧缺乏理论性的指导, 不同惯性权重的选择可能导致算法不同的收敛速度甚至不收敛。当惯性权重较大时, 算法的全局寻优能力较强; 当惯性权重较小时, 算法的局部寻优能力较强。为了避免粒子群算法陷入局部最优以及收敛速度过慢的问题, 文献[15]提出将惯性权重设置为呈线性递减的形式:

$ w = {w_{{\rm{start}}}} - ({w_{{\rm{start}}}} - {w_{{\rm{end}}}}) \times t/{t_{{\rm{max}}}} $

(5)

其中:t_max为最大迭代次数; w_start和w_end分别表示初始惯性权重和终止惯性权重, 通常w_start=0.9, w_end=0.4。由式(5)可知, 算法在开始时具有良好的全局搜索性能, 能够迅速定位到接近全局最优点的位置, 而在后期具有良好的局部搜索能力, 能够准确地得到全局最优解。

标准测试函数说明w从0.9减小到0.4时能极大地改善PSO算法的性能。但是也存在缺陷:迭代初期, 即使粒子已接近全局最优点由于其局部搜索能力较弱也可能会被错过, 迭代后期由于粒子全局搜索能力变弱, 容易陷入局部最优; 最大迭代次数较难预测, 从而影响算法的性能。为此需要增加粒子的多样性, 避免PSO早熟。多子群进化策略是目前增加粒子多样性的重要方法之一。

2.2 多子群进化策略

LVBJERG于2001年首次提出了多子群进化策略^[16], 即将群体划分为多个子种群分别独立进化, 在进化一定代数之后, 子种群之间依据一定的迁移规则进行个体迁移, 进而增加粒子向不同粒子学习的概率, 避免全体粒子收敛于同一个局部极值点。

为了进一步提高PSO算法求解大规模优化问题整体性能, 本研究提出的DPSO-MR算法采用多子群进化策略来实现PSO算法的并行化。

算法实现中最重要的参数是迁移拓扑结构和迁移方法^[17-18]。常见的迁移拓扑结构有链式拓扑、层叠式拓扑、环形拓扑等。其中, 环形拓扑结构有多种实现形式。在DPSO-MR算法中采用更适合于并行进化算法的环+1+2拓扑结构^[19](见图 2)。迁移方法采用的是源种群和目标种群依据“优-差”进行替换, 即用源种群最优的n个体替换目标种群最差的n个个体。

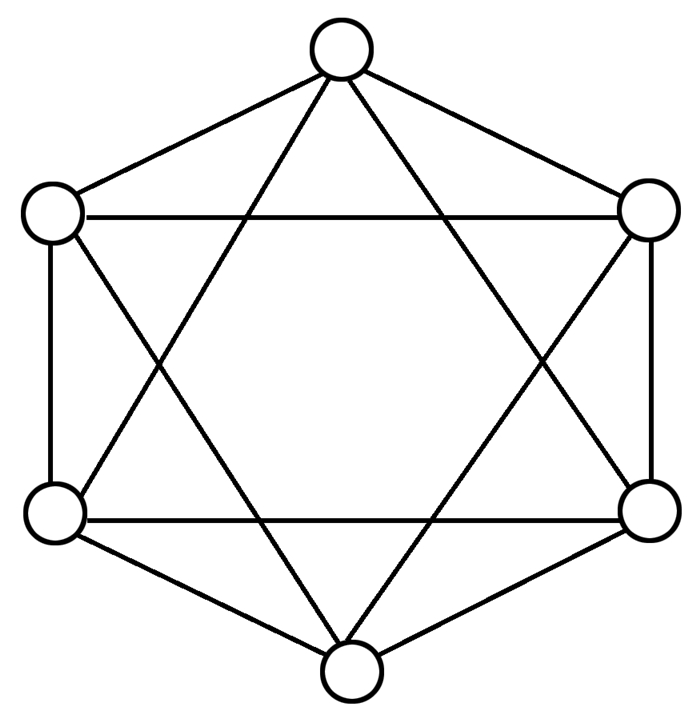
图 2 环+1+2拓扑结构 Figure 2 Topology ring+1+2

多子群进化策略不仅可以有效降低计算任务时间消耗, 而且可以明显改善算法的全局搜索能力, 从而维持粒子的多样性, 提高收敛速率, 平衡算法的全局搜索与局部搜索能力。

2.3 DPSO-MR的实现

算法总体思想将要处理的数据存储为key-value对, 其格式为[key_i, value_i], 其中:m为种群数目; i=1, 2, …, m; key_i是1个整数, 是第i个子种群的索引; value_i是1个列表, 包含第i个子种群中所有个体。

为了降低重启Map的负载, 将整个种群分成相对独立的子种群, 同时独立进化各个子种群, 在2个子种群间通过迁移操作进行个体移动。

本研究依据环+1+2拓扑结构来进行子种群之间的个体迁移操作, 每个子种群节点都与4个节点相邻, 个体的迁移只在相邻的节点间进行。

由于Map的并行操作, 已经将总任务分解, 并分配给集群运行。而每个Map任务都是1个子群的独立进化过程。因此, 算法不采用Reduce排序汇总, 产生中间数据直接存入HDFS。这样可以在一定程度上提高效率, 缩短时间。

算法描述如下:

算法1 DPSO-MR算法描述

{

步骤1 初始化参数。

(a) 设定子种群数目, 设置最大迭代代数, 初始迭代代数k=0;

(b) 设定子种群粒子规模, 并随机初始化粒子位置和速度;

步骤2 检查算法是否符合终止条件。

如果符合终止条件, 则输出全局最优粒子, 算法停止, 否则转到步骤3。

步骤3 子种群进化。

(a) 从HDFS中读取子种群;

(b) 独立进化每一个子种群:

计算粒子适应度值, 根据式(5)计算惯性权重, 根据式(3)~(4)更新粒子速度位置和速度, 找出每个子种群的最优粒子和全局最优粒子。

步骤4 依据环+1+2拓扑结构, “优-差”迁移方法迁移个体。

步骤5 子种群写入HDFS。

步骤6 k=k+1。

步骤7 转到步骤2。

}

3 试验与分析 3.1 算法参数设置及测试函数

为了验证本研究提出的DPSO-MR算法在求解大规模优化问题的有效性, 本研究选用经典PSO算法、协同差分演化算法(differential evolution with cooperative coevolution, DECCG)^[20], 基于MapReduce模型的差分进化算法(differential evolution based on MapReduce, DE-MR)进行对比试验。文中引入了13个Benchmark测试函数^[21]进行分析, 表 1列出了这些Benchmark测试函数的名称、表达式、定义域、全局最优值等, 其中, f₁~f₇为单峰函数, f₈~f₁₃为多峰函数。

表 1 测试函数表 Table 1 Benchmark functions

名称	表达式	定义域	最优解
Sphere Model	${f_1}\left( x \right) = \sum\limits_{i = 1}^n {x_i^2} $	[-100, 100]	0
Schwefel's Problem 2.22	${f_2}\left( x \right) = \sum\limits_{i = 1}^n {\left\| {{x_i}} \right\|} + \prod\limits_{i = 1}^n {\left\| {{x_i}} \right\|} $	[-10, 10]	0
Schwefel's Problem 1.2	${f_3}\left( x \right) = \sum\limits_{i = 1}^n {{{\left( {\sum\limits_{j = 1}^i {{x_j}} } \right)}^2}} $	[-100, 100]	0
Schwefel's Problem 2.21	f₄(x)=max_i{\|x_i\|, 1≤i≤n}	[-100, 100]	0
Generalized Rosenbrock's Function	${f_5}\left( x \right) = \sum\limits_{i = 1}^{n - 1} {\left[ {100{{\left( {{x_{i + 1}} - x_i^2} \right)}^2} + {{\left( {{x_i} - 1} \right)}^2}} \right]} $	[-30, 30]	0
Step Function	${f_6}\left( x \right) = \sum\limits_{i = 1}^n {{{\left( {\left\| {{x_i} + 0.5} \right\|} \right)}^2}} $	[-100, 100]	0
Quartic with Noise	${f_7}\left( x \right) = \sum\limits_{i = 1}^n {ix_i^4} + {\rm{random[0, 1)}}$	[-1.28, 1.28]	0
Generalized Schwefel's Problem 2.26	${f_8}\left( x \right) = \sum\limits_{i = 1}^n { - {x_i}\sin \left( {\sqrt {\left\| {{x_i}} \right\|} } \right)} $	[-500, 500]	-D×4.189 829×10²
Generalized Rastrigin's Function	${f_9}\left( x \right) = \sum\limits_{i = 1}^n {\left[ {x_i^2 - 10\cos \left( {2\pi {x_i}} \right) + 10} \right]} $	[-5.12, 5.12]	0
Ackley's Function	${f_{10}}\left( x \right) = - 20\exp \left( { - 0.2\sqrt {\frac{1}{2}\sum\limits_{i = 1}^n {x_i^2} } } \right) - \exp \left( {\frac{1}{n}\sum\limits_{i = 1}^n {\cos 2\pi {x_i}} } \right) + 20 + e$	[-32, 32]	0
Generalized Griewank Function	${f_{11}}\left( x \right) = \frac{1}{{4\;000}}\sum\limits_{i = 1}^n {x_i^2} - \prod\limits_{i = 1}^n {\cos \left( {\frac{{{x_i}}}{{\sqrt i }}} \right) + 1} $	[-600, 600]	0
Generalized Penalized Functions 1	${f_{12}}\left( x \right) = \frac{\pi }{n}\left\{ {10{{\sin }^2}\left( {\pi {y_i}} \right) + \sum\limits_{i = 1}^{n - 1} {{{\left( {{y_i} - 1} \right)}^2}\left[ {1 + 10{{\sin }^2}\left( {\pi {y_{i + 1}}} \right)} \right] + {{\left( {{y_n} - 1} \right)}^2}} } \right\} + \sum\limits_{i = 1}^n {u\left( {{x_i},10,100,4} \right)} $	[-50, 50]	0
Generalized Penalized Functions 2	${f_{13}}\left( x \right) = 0.1\left\{ {{{\sin }^2}\left( {3\pi {x_1}} \right) + \sum\limits_{i = 1}^{n - 1} {{{\left( {{x_i} - 1} \right)}^2}\left[ {1 + {{\sin }^2}\left( {3\pi {x_{i + 1}}} \right)} \right] + \left( {{x_n} - 1} \right)\left[ {1 + {{\sin }^2}\left( {2\pi {x_n}} \right)} \right]} } \right\} + \sum\limits_{i = 1}^n {u\left( {{x_i},5,100,4} \right)} $	[-50, 50]	0
注：${y_i} = 1 + \frac{1}{4}\left( {{x_i} + 1} \right),u\left( {{x_i},a,k,m} \right) = \left\{ {\begin{array}{*{20}{l}} {k{{\left( {{x_i} - a} \right)}^m},{x_i} > a,}\\ {0, - a \le {x_i} \le a,}\\ {k{{\left( { - {x_i} - a} \right)}^m},{x_i}< - a.} \end{array}} \right.$

表 1 测试函数表 Table 1 Benchmark functions

算法参数设置如下:为了增强可比性, 经典PSO算法和DPSO-MR算法的c₁=c₂=2, 进化的惯性权重w从0.9线性递减至0.4, 试验将种群平均分为20个子种群, 种群总规模为1 000, 迁移频率为500代(也即是每隔500代进行一次迁移), 迁移数量为15个个体; DECCG算法采用原文献参数设置; DE-MR算法的缩放因子F=0.5, 交叉概率CR=0.5, 种群规模为1 000。500维、1 000维都以评估次数达到D×5 000次为结束条件(D为维数)。为了排除随机性, 针对每个函数, 试验以25次独立试验的统计结果进行分析。试验使用8台x86结构的计算机组建集群, 每台机器配置一致:64bit core i7 cpu, 主频3.4G, 内存8G, Ubuntu13.10操作系统, 安装使用Hadoop2.2.0平台, 算法采用Eclipse环境, Java语言编程实现。

3.2 算法精度比较分析

试验统计结果(最优值, 最差值, 平均值及方差)见表 2所示。

表 2 收敛性试验结果表 Table 2 The experimental results of convergence

问题	算法	最优值		最差值		平均值		方差
问题	算法	500维	1 000维	500维	1 000维	500维	1 000维	500维	1 000维
f₁	PSO	1.61×10⁵	2.04×10⁶	2.57×10⁵	2.72×10⁶	2.11×10⁵	2.30×10⁶	1.50×10⁵	2.79×10⁴
	DECCG	9.46×10^-33	4.96×10^-29	1.75×10^-31	1.58×10^-28	5.04×10^-32	9.61×10^-29	3.31×10^-32	3.11×10^-29
	DPSO-MR	0	0	0	0	0	0	0	0
	DE-MR	1.61×10^-8	3.6 5×10^-4	1.57×10^-7	1.17×10^-3	5.94×10^-8	7.09×10^-4	3.92×10^-8	2.36×10^-4
f₂	PSO	1.18×10⁴	1.04×10⁵	7.41×10³	9.87×10⁴	2.23×10⁴	7.16×10⁴	1.80×10⁴	3.30×10⁴
	DECCG	9.14×10^-17	3.68×10^-15	1.00×10^-16	8.16×10^-14	1.156×10^-16	1.70×10^-14	9.25×10^-17	1.77×10^-14
	DPSO-MR	0	0	2.17×10³	4.53×10³	6.21×10²	8.25×10²	6.88×10²	1.15×10³
	DE-MR	2.90×10^-6	3.18×10^-3	1.54×10^-5	6.61×10^-3	7.24×10^-6	4.94×10^-3	2.50×10^-6	8.33
f₃	PSO	2.39×10⁷	7.14×10⁸	4.36×10⁷	9.93×10⁸	3.35×10⁷	8.68×10⁸	4.78×10⁶	6.51×10⁷
	DECCG	9.57×10^-15	2.25×10^-4	1.05×10^-14	2.80×10^-3	2.41×10^-14	1.20×10^-3	1.87×10^-14	6.70×10^-4
	DPSO-MR	0	0	0	0	0	0	0	0
	DE-MR	1.76×10⁶	7.57×10⁶	2.83×10⁶	1.13×10⁷	2.49×10⁶	9.39×10⁶	2.48×10⁵	9.46×10⁵
f₄	PSO	3.56×10²	3.73×10²	3.84×10²	4.15×10²	3.73×10²	4.01×10²	6.94	7.98
	DECCG	1.38×10^-7	2.22×10^-2	4.17×10^-7	4.09×10^-2	2.78×10^-7	3.19×10^-2	6.86×10^-8	4.72×10^-3
	DPSO-MR	0	0	4.58×10^-265	3.14×10^-284	1.83×10^-266	1.28×10^-285	0	0
	DE-MR	4.58×10¹	72.2	4.84×10¹	7.66×10¹	4.72×10²	7.56×10¹	6.27×10^-1	9.54×10^-1
f₅	PSO	3.77×10¹¹	9.95×10¹²	7.33×10¹¹	1.02×10¹³	5.42×10¹¹	9.23×10¹²	7.90×10¹⁰	1.29×10¹²
	DECCG	4.90×10²	9.87×10²	4.92×10²	9.85×10²	4.91×10²	9.86×10²	0.49	0.411
	DPSO-MR	4.98×10²	9.98×10²	4.99×10²	9.99×10²	4.99×10²	9.99×10²	0.221	0.200
	DE-MR	1.88×10³	4.99×10³	2.52×10³	6.22×10³	2.25×10³	5.58×10³	1.71×10³	3.23×10²
f₆	PSO	1.60×10⁵	2.04×10⁶	2.62×10⁵	2.52×10⁶	2.10×10⁵	2.30×10⁶	2.86×10⁴	1.29×10⁵
	DECCG	0	0	0	0	0	0	0	0
	DPSO-MR	0	0	0	0	0	0	0	0
	DE-MR	0	0	0	0	0	0	0	0
f₇	PSO	1.03×10¹²	2.81×10¹³	9.80×10¹¹	4.24×10¹³	1.07×10¹²	3.48×10¹³	2.32×10¹¹	3.87×10¹²
	DECCG	7.56×10^-5	1.50×10^-3	4.89×10^-4	3.70×10^-3	2.73×10^-4	2.62×10^-3	1.58×10^-4	6.68×10^-4
	DPSO-MR	1.04×10^-9	2.32×10^-8	8.77×10^-7	8.92×10^-7	2.13×10^-7	2.50×10^-7	1.98×10^-7	2.23×10^-7
	DE-MR	2.17×10^-1	6.49×10^-1	2.75×10^-1	7.81×10^-1	2.59×10^-1	7.16×10^-1	1.23×10^-2	3.18×10^-2
f₈	PSO	-9.18×10⁴	-1.44×10⁵	-8.30×10⁴	-1.22×10⁵	-8.77×10⁴	-1.34×10⁵	2.42×10³	4.51×10³
	DECCG	-2.09×10⁵	-4.19×10⁵	-2.09×10⁵	-4.19×10⁵	-2.09×10⁵	-4.19×10⁵	1.41×10^-7	9.28×10^-11
	DPSO-MR	-2.80×10²⁵⁵	-1.16×10²³⁸	-Inf	-2.92×10¹⁸¹	-Inf	-Inf	NaN	NaN
	DE-MR	-2.09×10⁵	-4.04×10⁵	-2.09×10⁵	-4.06×10⁵	-2.09×10⁵	-4.04×10⁵	1.46×10^-3	2.03×10³
f₉	PSO	1.68×10⁵	2.13×10⁶	2.55×10⁵	2.76×10⁶	2.07×10⁵	2.33×10⁶	2.11×10⁴	1.35×10⁵
	DECCG	0	0	0	3.55×10^-14	0	1.25×10^-14	0	7.49×10^-15
	DPSO-MR	0	0	0	0	0	0	0	0
	DE-MR	38.7	483	103	708	69.6	584	17	60.3
f₁₀	PSO	21.3	21.5	21.5	21.6	21.5	21.5	0.055 5	0.037 7
	DECCG	4.00×10^-14	1.15×10^-13	6.13×10^-14	1.39×10^-13	5.23×10^-14	1.27×10^-13	5.44×10^-15	7.11×10^-15
	DPSO-MR	4.44×10^-16	4.44×10^-16	4.44×10^-16	4.44×10^-16	4.44×10^-16	4.44×10^-16	0	0
	DE-MR	2.65×10^-6	3.82×10^-4	6.82×10^-6	7.72×10^-4	4.53×10^-6	5.05×10^-4	1.05×10^-6	9.90×10^-5
f₁₁	PSO	36.5	502	64.4	666	49.5	575	5.95	41.5
	DECCG	0	6.66×10^-16	2.22×10^-16	1.33×10^-15	1.38×10^-16	9.50×10^-16	6.63×10^-17	1.44×10^-16
	DPSO-MR	0	0	0	0	0	0	0	0
	DE-MR	1.87×10^-9	2.49×10^-5	2.89×10^-8	1.19×10^-4	9.56×10^-9	5.77×10^-5	5.59×10^-9	2.47×10^-5
f₁₂	PSO	2.73×10¹¹	5.52×10¹²	6.58×10¹¹	8.60×10¹²	4.10×10¹¹	6.99×10¹²	9.37×10¹⁰	7.75×10¹¹
	DECCG	2.20×10^-23	6.20×10^-28	9.16×10^-23	1.95×10^-27	4.97×10^-23	1.24×10^-27	1.79×10^-23	3.30×10^-28
	DPSO-MR	0.776	0.959	1.16	1.17	1.01	1.10	0.121	0.066 4
	DE-MR	2.21×10^-9	2.30×10^-4	2.70×10^-8	0.088 5	8.13×10^-9	0.010 8	5.84×10^-9	0.020 5
f₁₃	PSO	3.23×10¹¹	9.82×10¹²	7.09×10¹¹	1.01×10¹³	4.89×10¹¹	7.87×10¹²	1.14×10¹¹	8.78×10¹¹
	DECCG	8.76×10^-20	5.27×10^-24	0.011	0.011	1.76×10^-3	2.64×10^-3	4.11×10^-3	4.79×10^-3
	DPSO-MR	49.7	99.7	49.8	99.8	49.8	99.8	0.019	0.026 2
	DE-MR	-1.15	-1.14	-1.15	-1.14	-1.15	-1.14	5.49×10^-7	6.32×10^-3

表 2 收敛性试验结果表 Table 2 The experimental results of convergence

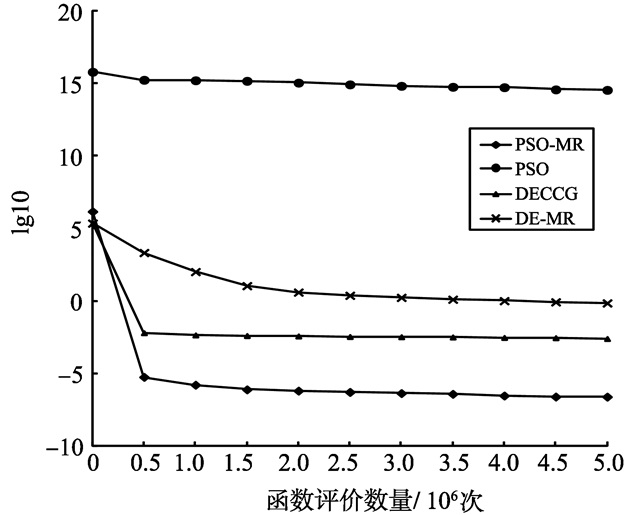
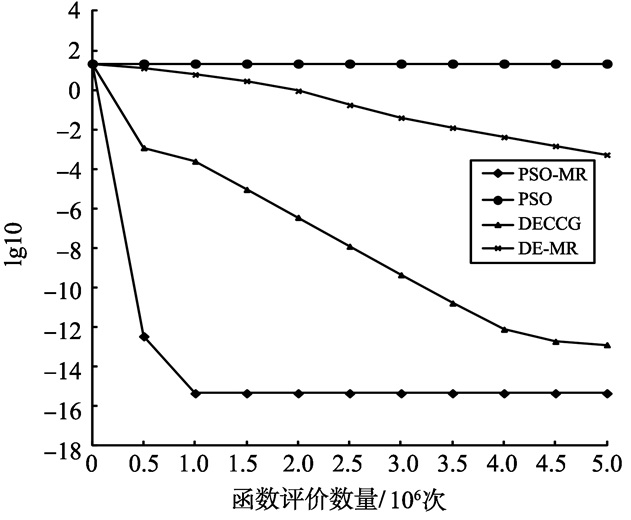
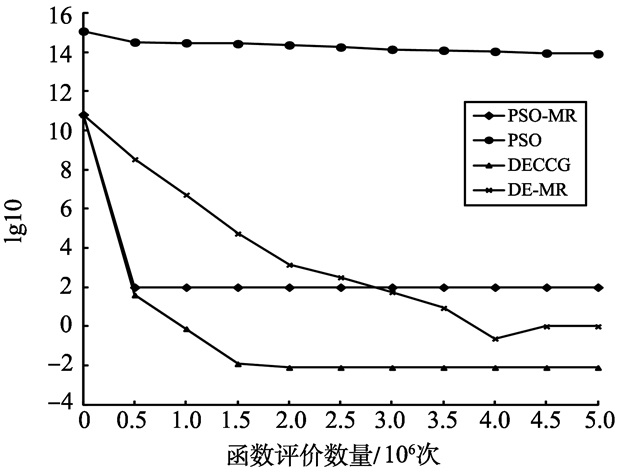
通过比较分析, DPSO-MR算法在大多数情况下求解性能都优于其他算法, 而经典PSO算法在维数500和维数1 000的情况下, 全部都陷入局部最优, 且求解精度远不如DECCG算法、DPSO-MR算法和DE-MR算法。表明在基于MapReduce模型的分布式计算平台上算法的运行速度大幅度地加快, 同时通过多子群进化策略, 使PSO算法跳出局部最优, 最终依靠Hadoop集群高速运行速度快速找到最优解。图 3~8给出了6个测试函数f₁、f₃、f₄、f₇、f₁₀、f₁₃随着函数评价数量的适应度值进化曲线。图中使用的数据是算法25次独立优化的平均值, 横坐标为函数评价数量, 纵坐标为lg10(适应度值)。从收敛曲线看出, DPSO-MR算法在进化过程中, 具有较强的收敛能力, 且能够持续的寻找全局最优解, 在收敛精度、收敛速率上优于其它3种算法, 较好的提升了PSO算法求解的整体性能。

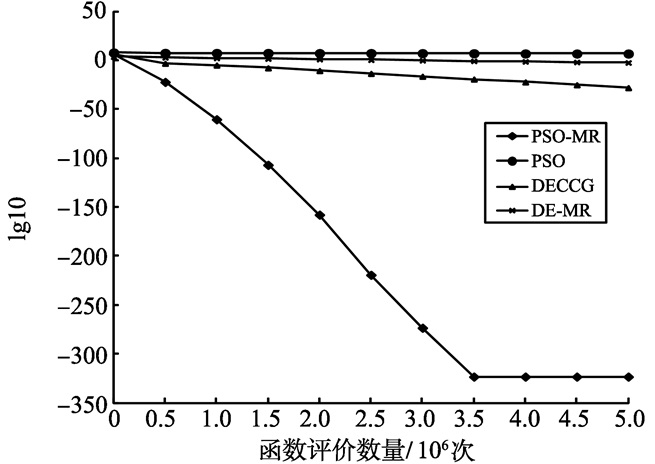
图 3 f₁函数收敛曲线图 Figure 3 The Convergence figure of Function f₁

图 4 f₃函数收敛曲线图 Figure 4 The Convergence figure of Function f₃

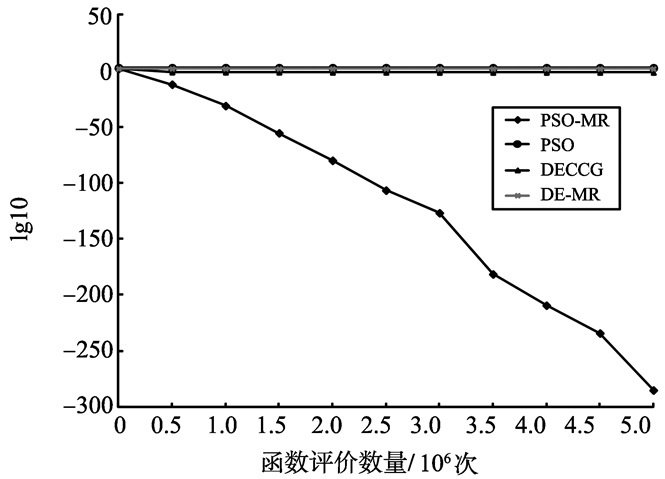
图 5 f₄函数收敛曲线图 Figure 5 The Convergence figure of Function f₄

图 6 f₇函数收敛曲线图 Figure 6 The Convergence figure of Function f₇

图 7 f₁₀函数收敛曲线图 Figure 7 The Convergence figure of Function f₁₀

图 8 f₁₃函数收敛曲线图 Figure 8 The Convergence figure of Function f₁₃

3.3 加速比比较分析

对于表 1中的13个1 000维函数, DPSO-MR算法选择1到7个数据节点进行试验, 结束条件为适应值函数的评价数量达到5.0×10⁶, 记录每个函数在不同数据节点下完成任务的平均消耗时间, 具体结果见表 3。

表 3 加速性能试验表 Table 3 Acceleration experiment ms

问题	节点数
问题	1	2	3	4	5	6	7
f₁	315 052	251 394	211 999	200 634	195 184	202 453	197 359
f₂	297 493	254 194	210 242	204 178	196 089	201 893	197 122
f₃	1 286 796	1 258 964	994 933	1 017 986	997 657	987 413	973 340
f₄	296 225	251 576	211 380	198 802	191 765	199 988	196 007
f₅	299 975	253 474	214 156	201 197	194 927	198 423	196 846
f₆	300 483	253 819	213 185	200 758	195 178	199 799	195 680
f₇	299 053	254 605	212 147	201 949	193 403	199 534	195 514
f₈	393 981	296 593	283 181	261 404	220 788	242 939	242 554
f₉	331 539	256 421	239 411	219 693	209 020	219 812	215 700
f₁₀	333 058	259 569	235 472	218 926	207 115	218 761	215 224
f₁₁	333 075	259 509	242 410	224 743	211 628	220 322	223 706
f₁₂	405 060	300 737	282 382	244 818	224 748	257 396	258 203
f₁₃	344 784	270 318	254 363	236 934	224 133	227 538	234 587
平均值	402 813	340 090	292 712	279 386	266 280	275 098	272 450

表 3 加速性能试验表 Table 3 Acceleration experiment ms

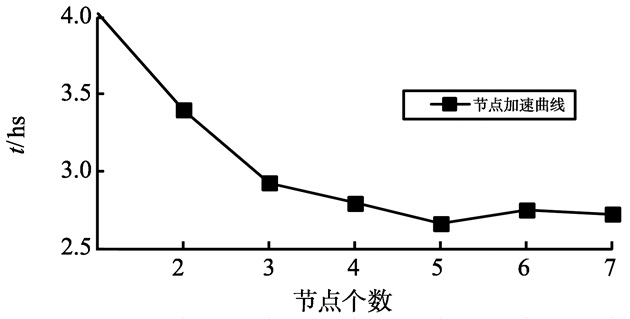
从表 3的结果来看, 随着节点数的逐步增加, 执行算法所消耗的时间在不断减少, 当数据节点数增加到5个时, 算法所消耗的时间最少。当数据节点数增加到6个及以上时, 并不能降低算法所消耗的时间。

经分析得知, 这与DPSO-MR算法和集群的设置有关。在MapReduce模型中, 1个子种群对应1个Map任务, 集群中每个数据节点Map任务的最大执行数为4。算法中设置子种群数为20个, 为了使集群资源得到充分利用, 即每个数据节点Map任务数达到最大, 数据节点数为5个时能充分使用资源。当增加数据节点数时, 必然会有部分节点不能充分使用资源, 而多出来的节点却会带来通信上的消耗。因此, 继续增加节点不能有效减少算法的执行时间。

图 9的加速性能曲线证明了以上分析结果。

图 9 加速性能曲线图 Figure 9 Acceleration figure

4 结论

为了提高PSO算法对大规模优化问题的性能, 提出一种基于MapReduce模型的分布式粒子群算法。算法采用了分布式并行编程模型MapReduce, 引入了惯性权重线性递减权值策略和多子群进化策略。惯性权重线性递减权值策略有利于改善算法的性能和效率; 多子群进化策略有利于降低计算任务时间消耗、提高了粒子的多样性, 平衡了算法的全局搜索与局部搜索能力。算法突破了传统单机处理模式的限制。选择了13个500维、1 000维基准测试函数仿真试验表明:DPSO-MR算法不仅收敛速度快, 加速性能高, 而且算法具有良好的稳定性。

参考文献

[1]	KENNEDY J, EBERHART R C.Particle swarm optimization[C]//IEEE International Conference on Neural NetworksPerth. Australia:IEEE, 1995:1942-1948.
[2]	陈永刚, 魏汪洋, 肖春宝. 粒子群优化算法在函数优化上的研究与发展[J]. 西安邮电学院学报, 2009, 14 (3) : 113-116 CHEN Yonggang, WEI Wangyang, XIAO Chunbao. Research and development of particle swarm optimization algorithm in function optimazation[J]. Journal of Xi'an University of Post and Telecommunications, 2009, 14 (3) : 113-116
[3]	孟庆宽, 仇瑞承, 张漫, 等. 基于改进粒子群优化模糊控制的农业车辆导航系统[J]. 农业机械学报, 2015, 46 (3) : 29-36 MENG Qingkuan, QIU Ruicheng, ZHANG Man, et al. Navigation system of agricultural vehicle based on fuzzy logic controller with improved particle swarm optimization algorithm[J]. Journal of Transactions of the Chinese Society for Agricultural Machinery, 2015, 46 (3) : 29-36
[4]	徐乐华, 凌卫新, 熊丽琼. 基于面向对象自适应粒子群算法的神经网络训练[J]. 计算机应用研究, 2009, 26 (1) : 111-113 XU Lehua, LIN Weixin, XIONG Liqiong. Neural network training based on object-oriented adaptive particle swarm optimization[J]. Journal of Application Research of Computers, 2009, 26 (1) : 111-113
[5]	张鑫源, 胡晓敏, 林盈. 遗传算法和粒子群优化算法的性能对比分析[J]. 计算机科学与探索, 2014, 8 (1) : 90-102 ZHANG Xinyuan, HU Xiaomin, LIN Ying. Comparisons of genetic algorithm and particle swarm optimization[J]. Journal of Frontiers of Computer Science & Technology, 2014, 8 (1) : 90-102
[6]	金敏, 鲁华祥. 一种遗传算法与粒子群优化的多子群分层混合算法[J]. 控制理论与应用, 2013, 30 (10) : 1231-1238 JIN Min, LU Huaxiang. A multi-subgroup hierarchical hybrid of genetic algorithm and particle swarm optimization[J]. Journal of Control Theory & Applications, 2013, 30 (10) : 1231-1238
[7]	汪靖, 吴志健. 在GPU上求解大规模优化问题的反向策略的PSO算法[J]. 武汉大学学报(理学版), 2011, 57 (2) : 148-154 WANG Jing, WU Zhijian. Opposition-based particle swarm optimization for solving large scale optimization problems on graphic process unit[J]. Journal of Wuhan University (Science Edition), 2011, 57 (2) : 148-154
[8]	DEAN J, GHEMAWAT S. MapReduce: simplified data processing on large clusters[J]. Proceedings of Operating Systems Design and Implementation, 2004, 51 (1) : 107-113
[9]	DEAN J, GHEMAWAT S. MapReduce: a flexible data processing tool[J]. Communications of the Acm, 2010, 53 (1) : 72-77 DOI:10.1145/1629175
[10]	MCNABB A W, MONSON C K, SEPPI K D. Parallel PSO using MapReduce[C]//IEEE Congress on Evolutionary Computation. Singapore:IEEE, 2007:7-14.
[11]	马汉达, 杨丽娜. 基于Hadoop的PSO-KM聚类算法的并行实现[J]. 信息技术, 2015, 39 (7) : 90-94 MA Handa, YANG Lina. Parallel implementation of PSO-KM clustering algorithm based on Hadoop[J]. Journal of information technology, 2015, 39 (7) : 90-94
[12]	黄奕平, 万剑怡, 万中英, 等. 基于MapReduce的粒子群投影寻踪模型的设计与实现[J]. 江西师范大学学报(自然科学版), 2012, 36 (4) : 388-394 HUANG Yiping, WAN Jianyi, WAN Zhongying, et al. The design and implementing for projection pursuit model using PSO based on MapReduce[J]. Journal of Jiangxi Normal University (Natural Science Edition), 2012, 36 (4) : 388-394
[13]	SHI Y, EBERHART R C. Particle swarm optimization with fuzzy adaptive inertia weight[J]. International Journal of Bio Inspired Computation, 2001, 1 (12) : 32-49
[14]	RANGER C, RAGHURAMAN R, PENMETSA A, et al. Evaluating MapReduce for multi-core and multiprocessor systems[C]//IEEE 13th International Symposium on High Performance Computer Architecture. Scottsdale, USA: IEEE, 2007:13-24.
[15]	SHI Y, EBERHART R C. A modified particle swarm optimizer[C]//Proceedings of IEEE World Congress on Computational Intelligence. Scottsdale, USA: IEEE, 1998:69-73.
[16]	LØVBJERG M, RASMUSSEN T K, KRINK T. Hybrid particle swarm optimizer with breeding and subpopulations[C]//Proceedings of International Conference on Genetic and Evolutionary Computation. San Francisco, USA:ACM, 2001:469-476.
[17]	王雪飞, 王芳, 邱玉辉. 一种具有动态拓扑结构的粒子群算法研究[J]. 计算机科学, 2007, 34 (3) : 205-207 WANG Xuefei, WANG Fang, QIU Yuhui. Research on a Novel Particle Swarm Algorithm with Dynamic Topology[J]. Journal of Computer Science, 2007, 34 (3) : 205-207
[18]	石松, 陈云. 层次环形拓扑结构的动态粒子群算法[J]. 计算机工程与应用, 2013, 49 (8) : 1-5 SHI Song, CHEN Yun. Dynamic particle swarm optimization algorithm with hierarchical ring topology[J]. Journal of Computer Engineering and Applications, 2013, 49 (8) : 1-5
[19]	RUCIŃSKI M, IZZO D, BISCANI F. On the impact of the migration topology on the island model[J]. Parallel Computing, 2010, 36 (10) : 555-571
[20]	YANG Z Y, TANG K, YAO X. Large scale evolutionary optimization using cooperative coevolution[J]. Information Sciences, 2008, 178 (15) : 2985-2999 DOI:10.1016/j.ins.2008.02.017
[21]	YAO X, LIU Y, LIN G M, et al. Evolutionary programming made faster[J]. IEEE Transactions On Evolutionary Computation, 1999, 3 (2) : 82-102 DOI:10.1109/4235.771163