岩体是由完整的岩石基体和裂隙组成, 且岩石基体的渗透系数远小于裂隙的渗透系数, 一般认为, 岩体内的渗流主要由裂隙控制[1-2]。当隧道开挖时, 岩体内赋存的水体将通过裂隙渗透到掌子面内, 从而影响隧道周边岩体的水力学特性, 进而影响隧道建设的安全性。当隧道在长距离反坡施工期间遭受突涌水, 且排水能力不足时, 隧道易被淹没, 轻则影响工期, 造成经济损失, 重则造成人员伤亡[3]。随着我国隧道建设向地质环境复杂的西部山区转移, 比如湖北沪蓉西齐岳山隧道出口段反坡施工中, 突遇大型涌水, 导致隧道被淹, 延误工期超过半年, 造成大量的经济财产损失[4-5]。所以, 亟需解决隧道开挖过程中涌水量预测难题。
国内外很多学者对隧道涌水量已做过相关研究。王晓明等人采用蒙特卡洛方法建立岩体裂隙网络, 对隧道涌水量进行概率研究, 最后提出一种概率预测方法[6]; 喻成云等人基于大量的实际隧道涌水量数据, 利用数学统计方法, 建立了预测隧道涌水量的回归方程[7]; 刘牛生研究并制定了基于隧道涌水量变化的排水设置方案[8]。但在实际岩体中, 裂隙分布形态复杂, 且裂隙赋存于岩体内部, 其长度分布、开度变化、倾角、走向等参数均难以测得。根据大量的现场地质调查数据, 研究发现裂隙的长度一般服从对数正态分布、幂函数分布、分形分布、指数分布等[9-14], 其中, 幂函数分布被普遍接受, 并得到了大量应用[15-20]。顾博渊等人通过总结自20世纪80年代起提出的隧道涌水量预测模型, 认为其主要分为两大类:确定性数学模型方法和随机性数学模型分析方法[21-25], 前者包括降雨入渗法、比拟法、地下水径流法等, 后者包括灰色关联理论、时间序列分析法、黑箱理论等。赵继增探讨了青岛胶州湾海底隧道涌水断层全断面帷幕注浆技术[26]。张庆松等人针对岩溶隧道施工风险评价和突水灾害防治技术进行了深入研究[27]。通过文献调研发现, 很多学者主要研究了不同地质条件、不同隧道模型的涌水量预测问题, 尚没有考虑围岩内赋存水体深度、隧道直径和开挖距离对隧道涌水量的影响[28-31]。
近年来随着数值建模技术的进步和计算能力的发展, 离散裂隙网络模型被用来解决更加复杂的工程问题。围岩内的水体主要通过连通的裂隙网络渗透到隧道开挖的掌子面, 因此建立符合实际情况的离散裂隙网络模型, 对影响隧道涌水量的因素进行参数分析, 预测隧道涌水量是十分重要的任务。本研究基于蒙特卡洛方法, 建立符合实际情况的复杂岩体裂隙网络模型, 考虑隧道开挖距离、隧道直径、赋存于围岩内的水体深度等多因素的影响, 观测流体在裂隙内的分布规律, 最终得到预测隧道涌水量的多参数回归方程。本研究可为预测隧道涌水量、评估隧道在建设期的安全性提供理论和技术指导。
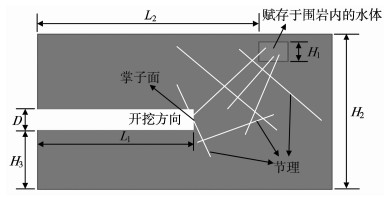
1 模型参数裂隙发育岩体内隧道开挖示意图如图 1所示。随着隧道开挖的推进, 隧道离赋存于围岩内的水体越来越近, 作用于掌子面的水压力不断增大, 其涌水量也逐渐加大。
|
图 1 裂隙发育岩体内隧道开挖示意图 Figure 1 Schematic of tunnel excavation in fractured rock masses |
岩体裂隙网络模型参数如表 1所示。
| 表 1 模型参数表 Table 1 Parameters of the model |
在20世纪80年代, 由于缺少现场地质调查数据, 国内外学者一般假设离散裂隙网络由长度相等的裂隙组成[32-36], 随着研究的深入和地质调查数据的增多, 近年来的研究发现自然界中裂隙的长度一般服从幂函数分布[12]、指数函数分布[14]和对数正态分布[37-38], 其中幂函数分布得到了最为广泛的应用[15-18, 39-40]。本研究假设裂隙长度服从幂函数分布, 如式(1):
| $ n = \alpha {l^{-a}}, $ | (1) |
式中:n为裂隙的数量; l为裂隙的长度; a为幂指数; α为正相关系数。幂指数a对裂隙的密度及裂隙网络渗透性有重要影响, 研究发现由于受岩体种类、地应力作用、调查范围、调查精度等影响, a一般取1.0~3.5[41-44], 本研究假设a=2.5。裂隙的长度可由式(2)计算得到:
| $ l = {l_{\min }}R_1^{-\frac{1}{a}}。 $ | (2) |
式中R1为0~1之间均匀分布的随机数。假设裂隙中心点(xi, yi)和倾角θ均匀随机分布, 则在x=[xg1, xg2], y=[yg1, yg2]的区域内生成裂隙网络模型时, 每一条裂隙的起点(xstart, ystart)和终点(xend, yend)的计算公式为
| $ \begin{array}{l} {x_{{\rm{start}}}} = {x_i}-l\cos \theta, \\ {y_{{\rm{start}}}} = {y_i}-l\sin \theta, \\ {x_{{\rm{end}}}} = {x_i} + l\cos \theta, \\ {y_{{\rm{end}}}} = {y_i}-l\sin \theta 。 \end{array} $ |
其中:xi∈[xg1, xg2]; yi∈[yg1, yg2]; θ∈[0, 2π]。由于裂隙内的流体一般为不可压缩的粘性牛顿流体, 所以假设裂隙内的流体流动服从立方定律
| $ Q = \frac{{w{e^3}}}{{12\mu }}\frac{{\Delta P}}{l}。 $ | (3) |
式中:Q为流量; e为裂隙的开度; P为压力; μ为粘度; w为裂隙的宽度, 在二维模型中, w=1。其中流量和压力线性相关, 和开度的立方成正比。流体的密度为998.2 kg/m3, 粘度为0.001 Pa·s。考虑到实际工程中很难测定裂隙的开度分布, 为简化计算, 假设所有的裂隙具有相同的开度e=100 μm。
2 离散裂隙网络模型及边界条件基于具有开源代码的二维离散元软件通用离散单元法程序(universal distinct element code, UDEC), 利用FISH语言, 自编函数建立裂隙网络模型和渗流计算程序。利用表 1的模型参数, 生成96个不同水体深度H1(H1=1~7 m)、不同隧道直径D(D=4~10 m)、不同开挖距离L1(L1=1~17 m)的复杂裂隙网络模型, 其中的三个模型如图 2所示。本研究的裂隙网络模型仅代表节理发育的坚硬岩体, 岩石基体的渗透性远小于裂隙的渗透性, 甚至可忽略不计的情况。

|
图 2 裂隙网络数值模型 Figure 2 Numerical models of fracture networks |
由于隧道开挖后要进行二衬并设置防水层, 所以假设流体从赋存于围岩内的水体流入裂隙网络模型, 从隧道掌子面流出, 其他边界的渗漏可忽略不计, 均设为不透水边界。当流入岩体的流量等于流出岩体的流量时, 认为流体流动达到稳态, 记录此时的流量, 即为通过隧道掌子面的涌水量。
3 结果及分析不同水体深度H1、不同隧道直径D、不同开挖距离L1的裂隙网络内流速分布如图 3所示, 灰色代表裂隙网络, 蓝色代表流量分布, 每条蓝色线宽为3×10-11m3/s。流体的主要流动路径由连接入口边界和出口边界的连通裂隙组成, 如图 3中黄色箭头所示, 此处裂隙内的流速最大, 离连接入口边界和出口边界的连通裂隙越远, 裂隙内的流速越小, 比如左上角和左下角的裂隙内流速基本为零。随着开挖距离的增加, 离水体越近, 可预测通过掌子面的涌水量越多。水体越深, 其水压力越大, 通过掌子面的涌水量也将越多。

|
图 3 流速分布示意图 Figure 3 Flow rate distributions |
通过改变水体深度H1、隧道直径D、开挖距离L1, 计算通过掌子面的涌水量, 结果如图 4所示。图中数据点代表数值计算结果, 曲线为拟合结果。结果表明, 当水体深度H1较小(图 4中H1=1, 4 m)时, 涌水量与开挖距离L1具有幂函数关系, 且随着隧道直径D的增加, Q~L1幂函数关系的正相关系数和指数均增加; 当水体深度H1较大(图 4中H1=7 m)时, 涌水量与开挖距离L1具有线性关系, 且随着隧道直径D的增加, 线性项系数和常数项均增加。

|
图 4 隧道涌水量和开挖距离关系曲线 Figure 4 Relationship of flow rate and excavation distance |
由于水体深度H1=1~4 m、隧道直径D=4~10 m、开挖距离L1=1~17 m, 共96种工况, 所以, 可建立考虑水体深度H1、隧道直径D和开挖距离L1的隧道涌水量预测公式。每一种工况对应的H1、D和L1的数值如表 2所示。
| 表 2 不同计算工况下隧道涌水量预测结果 Table 2 Predictions of flow rate for different cases |
通过Datafit数据拟合软件, 对表 2中的结果进行拟合, 结果发现隧道的涌水量和H1、D和L1呈指数函数关系:
| $ \begin{array}{l} Q = \exp (0.020\;8{L_1} + 0.031\;7{H_1} + \\ \;\;\;\;\;\;\;\;\;\;\;0.040\;9D-19.459)。 \end{array} $ | (4) |
结果表明, 系数0.040 9> 0.031 7> 0.020 8, 即对隧道涌水量的影响程度由高到低依次为D> H1>L1。将式(4)得到的预测结果和数值计算结果对比如图 5所示。分析发现, 二者能很好吻合, 相关系数R2>0.95。由此得出, 式(4)可用来预测隧道开挖过程中涌水量的动态变化。

|
图 5 预测结果和计算结果对比 Figure 5 Comparison of predicted and calculated results |
隧道涌水量预测公式(4)是基于裂隙平均开度为100 μm的假设而得到, 当实际岩体裂隙的平均开度发生变化时, 其涌水量也将发生变化。由式(3)可知, 流量和开度的三次方成正比, 所以, 对于任意平均开度为e的岩体裂隙网络模型, 隧道涌水量可通过式(5)预测得到:
| $ \begin{array}{l} Q = {(10\;000e)^3} \times \exp (0.020\;8{L_1} + 0.031\;7{H_1} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.040\;9D-19.459)。 \end{array} $ | (5) |
式中e的单位为m。
需要注意的是, 如果模型参数超出表 1的取值范围, 且二者相差不是很大时, 建议仍采用式(4)进行隧道涌水量的预测; 如果二者相差较大, 建议根据新的模型参数, 重新建模、计算, 拟合新的隧道涌水量预测公式。
4 结论建立了长度服从幂函数分布的离散裂隙网络数值模型, 针对不同水体深度、隧道直径和开挖距离共96种工况进行数值模拟, 计算通过隧道掌子面的涌水量, 最终拟合得到预测隧道涌水量的多参数回归方程。
(1) 流体的主要流动路径由连接入口边界和出口边界的连通裂隙组成, 此处裂隙内的流速最大, 离连接入口边界和出口边界的连通裂隙越远, 裂隙内的流速越小。
(2) 当水体深度H1较小(比如H1=1, 4 m)时, 涌水量与开挖距离L1具有幂函数关系, 且随着隧道直径D的增加, Q-L1幂函数关系的正相关系数和指数均增加; 当水体深度H1较大(比如H1=7 m)时, 涌水量与开挖距离L1具有线性关系, 且随着隧道直径D的增加, 线性项系数和常数项均增加。
(3) 基于Datafit数据拟合软件, 对96种工况的数值计算结果进行拟合, 发现隧道的涌水量Q和水体深度H1、隧道直径D和开挖距离L1呈指数函数关系, 这些参数对隧道涌水量影响程度由高到低依次为:隧道直径>水体深度>开挖距离。通过回归方程的预测结果和数值计算结果对比发现, 二者能很好吻合, 从而验证了该回归方程具有普适性, 可以对节理发育岩体内隧道涌水量进行动态预测。
但本研究仅考虑赋存于围岩内的水体深度、隧道直径和开挖距离三个因素对隧道涌水量的影响, 尚未考虑其他因素, 比如地质构造的几何分布、应力作用、隧道开挖引起的裂隙扩展等对涌水量的影响。因为复杂网络模型内的流固耦合机理较复杂, 迭代计算需要耗费大量的人力、物力, 常规计算机无法满足计算要求, 计算成本较高, 所以改进迭代算法、提高计算速度、考虑流固耦合作用将是接下来的研究重点, 今后条件允许时, 也需要针对实际隧道工程, 对预测隧道涌水量的经验公式进行验证应用。
| [1] | MIN K B, JING L. Numerical determination of the equivalent elastic compliance tensor for fractured rock masses using the distinct element method[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40 (6) : 795-816 DOI:10.1016/S1365-1609(03)00038-8 |
| [2] | MIN K B, RUTQVIST J, TSANG C F, et al. Stress-dependent permeability of fractured rock masses: a numerical study[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41 (7) : 1191-1210 DOI:10.1016/j.ijrmms.2004.05.005 |
| [3] |
李方东. 基于涌水量预估和动态监测的公路隧道长距离反坡排水施工技术及其应用[J].
隧道建设, 2015, 35 (12) : 1321-1330 LI Fangdong. Reverse slope drainage technology based on water inflow prediction and dynamic monitoring and its application in long tunnel[J]. Tunnel Construction, 2015, 35 (12) : 1321-1330 |
| [4] |
胡子平. 宜万铁路齐岳山隧道选线, 施工与管理[J].
铁道标准设计, 2010 (8) : 12-19 HU Ziping. Route selection, construction and management of Qiyueshan tunnel in Yiwan railway[J]. Railway Standard Desigh, 2010 (8) : 12-19 |
| [5] |
左玉杰. 反坡富水岩溶隧道抽排水系统的设置和应用[J].
铁道建筑技术, 2007 (4) : 26-29 ZUO Yujie. A rangement and application of the tunnel drainage system in the reverse-slope stratum with a bundant water[J]. Railway Construction Technology, 2007 (4) : 26-29 |
| [6] |
王晓明, 曹正波. 基于水均衡方法的隧道涌水量概率预测[J].
交通标准化, 2014, 42 (23) : 112-114 WANG Xiaoming, CAO Zhengbo. Probabilistic prediction of water inflow into a tunnel using water balance method[J]. Transport Standardization, 2014, 42 (23) : 112-114 |
| [7] |
喻成云.基于统计分析的西南岩溶区隧道涌水量预测探析[D].成都:成都理工大学, 2013.
YU Chengyun. Based on statistical analysis of southwest China karst tunnel inflow forecast analysis[D]. Chengdu: Chengdu University of Technology, 2013. |
| [8] |
刘牛生. 特长隧道涌水综合反坡排水施工技术[J].
建筑, 2010 (12) : 44 LIU Niusheng. Construction techniques for reverse slope drainage of a long tunnel[J]. Construction and Architecture, 2010 (12) : 44 |
| [9] | CHELIDZE T, GUEGUEN Y. Evidence of fractal fracture[J]. International Journal of Rock Mechanics and Mining Sciences, 1990, 27 (3) : 223-225 DOI:10.1016/0148-9062(90)94332-N |
| [10] | WATANABE K, TAKAHASHI H. Fractal geometry characterization of geothermal reservoir fracture networks[J]. Journal of Geophysical Research: Solid Earth, 1995, 100 : 521-528 DOI:10.1029/94JB02167 |
| [11] | WATANABE K, TAKAHASHI H. Parametric study of the energy extraction from hot dry rock based on fractal fracture network model[J]. Geothermics, 1995, 24 (2) : 223-236 DOI:10.1016/0375-6505(94)00049-I |
| [12] | KOLYUKHIN D, TORABI A. Power-law testing for fault attributes distributions[J]. Pure and Applied Geophysics, 2013, 170 (12) : 2173-2183 DOI:10.1007/s00024-013-0644-3 |
| [13] | DMITRIY K, ANITA T. Statistical analysis of the relationships between faults attributes[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 2012, 117 (B5) : 81-88 |
| [14] | TORABI A, BERG S S. Scaling of fault attributes: a review[J]. Marine and Petroleum Geology, 2011, 28 (8) : 1444-1460 DOI:10.1016/j.marpetgeo.2011.04.003 |
| [15] | CHILDS C, WALSH J J, WATTERSON J. A method for estimation of the density of fault displacements below the limits of seismic resolution in reservoir formations[J]. North Sea Oil and Gas Reservoirs-II, 1990 : 309-318 |
| [16] | SORNETTE A, DAVY P, SORNETTE D. Fault growth in brittle-ductile experiments and the mechanics of continental collisions[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 1993, 98 (B7) : 12111-12139 DOI:10.1029/92JB01740 |
| [17] | BOUR O, DAVY P. Connectivity of random fault networks following a power law fault length distribution[J]. Water Resources Research, 1997, 33 (7) : 1567-1583 DOI:10.1029/96WR00433 |
| [18] | REEVES D M, PARASHAR R, POHLL G, et al. The use of discrete fracture network simulations in the design of horizontal hillslope drainage networks in fractured rock[J]. Engineering Geology, 2013, 163 : 132-143 DOI:10.1016/j.enggeo.2013.05.013 |
| [19] | PARASHAR R, REEVES D M. On iterative techniques for computing flow in large two-dimensional discrete fracture networks[J]. Journal of Computational and Applied Mathematics, 2012, 236 (18) : 4712-4724 DOI:10.1016/j.cam.2012.02.038 |
| [20] | BAGHBANAN A, JING L. Hydraulic properties of fracture rock masses with correlated fracture length and aperture[J]. International Journal Rock Mechanics Mining Sciences, 2007, 44 (5) : 704-719 DOI:10.1016/j.ijrmms.2006.11.001 |
| [21] |
顾博渊, 史宝童, 黄嫚. 山岭隧道涌水量预测方法分类及相关因素分析[J].
隧道建设, 2015, 35 (12) : 1258-1263 GU Boyuan, SHI Baotong, HUANG Man. Classification of water inflow prediction methods for mountain-crossing tunnels and analysis on related factors[J]. Tunnel Construction, 2015, 35 (12) : 1258-1263 |
| [22] |
田海涛, 董益华, 王延辉. 隧道涌水量预测的研究[J].
水利与建筑工程学报, 2007, 5 (3) : 75-77 TIAN Haitao, DONG Yihua, WANG Yanhui. Study on forecasting for water-gushed yield of tunnel[J]. Journal of Water Resources and Architectural Engineering, 2007, 5 (3) : 75-77 |
| [23] |
姜爱民, 杨辉, 张明. 确定性数学模型方法预测隧道涌水量研究[J].
工程勘察, 2012, 40 (6) : 37-41 JIANG Aimin, YANG Hui, ZHANG Ming. Study on deterministic mathematical model for predicting water gushing yield of tunnel[J]. Geotechnical Investigation and Surveying, 2012, 40 (6) : 37-41 |
| [24] |
陶玉敬, 彭金田, 陶炳勋. 隧道涌水量预测方法及其分析[J].
四川建筑, 2007, 27 (6) : 109-110 TAO Yujing, PENG Jintian, TAO Bingxun. Study and analysis on forecasting for water-gushed yield of tunnel[J]. Sichuan Architecture, 2007, 27 (6) : 109-110 |
| [25] |
郑黎明. 隧道涌水灾害预测的随机性数学模型方法[J].
西南交通大学学报, 1998, 33 (3) : 273-278 ZHENG Liming. A stochastic mathematic method for predicting gushing water from tunnel surrounding rockmasses[J]. Journal of Southwest Jiaotong University, 1998, 33 (3) : 273-278 |
| [26] |
赵继增. 青岛胶州湾海底隧道涌水断层全断面帷幕注浆技术研究[J].
山东大学学报(工学版), 2009, 39 (6) : 116-120 ZHAO Jizeng. Study of full-face curtain grouting on water-burst fault F4-4 subsea tunnel in Qingdao Jiaozhou bay[J]. Journal of Shandong University (Engineering Science), 2009, 39 (6) : 116-120 |
| [27] |
张庆松, 李术才, 韩宏伟, 等. 岩溶隧道施工风险评价与突水灾害防治技术研究[J].
山东大学学报(工学版), 2009, 39 (3) : 106-110 ZHANG Qingsong, LI Shucai, HAN Hongwei, et al. Study on risk evaluation and water inrush disaster preventing technology during construction of karst tunnels[J]. Journal of Shandong University (Engineering Science), 2009, 39 (3) : 106-110 |
| [28] |
薛翊国, 李术才, 张庆松, 等. 隧道信息化施工地质灾害预警预报技术研究[J].
山东大学学报(工学版), 2008, 38 (5) : 25-30 XUE Yiguo, LI Shucai, ZHANG Qingsong, et al. Prediction and early-warning technology of geological hazards in tunnel informational construction[J]. Journal of Shandong University (Engineering Science), 2008, 38 (5) : 25-30 |
| [29] |
邱道宏, 钟世航, 李术才, 等. 陆地声纳法在隧道不良地质超前预报中的应用[J].
山东大学学报(工学版), 2009, 39 (4) : 17-20 QIU Daohong, ZHONG Shihang, LI Shucai, et al. Application of the land sonar method in tunnel defective geological advanced prediction[J]. Journal of Shandong University (Engineering Science), 2009, 39 (4) : 17-20 |
| [30] |
马秀媛, 李逸凡, 张立, 等. 数值方法在矿井涌水量预测中的应用[J].
山东大学学报(工学版), 2011, 41 (5) : 86-91 MA Xiuyuan, LI Yifan, ZHANG Li, et al. Numerical methods in predicting mine discharge[J]. Journal of Shandong University (Engineering Science), 2011, 41 (5) : 86-91 |
| [31] |
刘斌, 李术才, 张庆松, 等. 隧道地质灾害预警体系中岩溶裂隙水综合预报技术研究[J].
山东大学学报(工学版), 2009, 39 (3) : 115-121 LIU Bin, LI Shucai, ZHANG Qingsong, et al. Study of the prediction of karst-fractured groundwater in prediction and early warning system of tunnel geologic hazards[J]. Journal of Shandong University (Engineering Science), 2009, 39 (3) : 115-121 |
| [32] | ENGLMAN R, GUR Y, JAEGER Z. Fluid flow through a crack network in rocks[J]. Journal of Applied Mechanics, 1983, 50 (4a) : 707-711 DOI:10.1115/1.3167133 |
| [33] | ROBINSON P C. Connectivity of fracture systems-a percolation theory approach[J]. Journal of Physics A: Mathematical and General, 1983, 16 (3) : 605 DOI:10.1088/0305-4470/16/3/020 |
| [34] | ROBINSON P C. Numerical calculations of critical densities for lines and planes[J]. Journal of Physics A: Mathematical and General, 1984, 17 (14) : 2823 DOI:10.1088/0305-4470/17/14/025 |
| [35] | BALBERG I, ANDERSON C H, ALEXANDER S, et al. Excluded volume and its relation to the onset of percolation[J]. Physical Review B, 1984, 30 (7) : 3933-3943 DOI:10.1103/PhysRevB.30.3933 |
| [36] | GUEGUEN Y, DIENES J. Transport properties of rocks from statistics and percolation[J]. Mathematical Geology, 1989, 21 (1) : 1-13 DOI:10.1007/BF00897237 |
| [37] | SAHIMI M. Flow phenomena in rocks: from continuum models to fractals, percolation, cellular automata, and simulated annealing[J]. Reviews of Modern Physics, 1993, 65 (4) : 1393 DOI:10.1103/RevModPhys.65.1393 |
| [38] | ANDRADE JR J S, OLIVEIRA E A, MOREIRA A A, et al. Fracturing the optimal paths[J]. Physical Review Letters, 2009, 103 (22) : 225503 DOI:10.1103/PhysRevLett.103.225503 |
| [39] | DAVY P. On the frequency-length distribution of the San Andreas fault system[J]. Journal of Geophysical Research, 1993, 98 (B7) : 12141-12151 DOI:10.1029/93JB00372 |
| [40] | BOGDANOV I I, MOURZENKO V V, THOVERT J F, et al. Effective permeability of fractured porous media with power-law distribution of fracture sizes[J]. Physical Review E, 2007, 76 (3) : 73-82 |
| [41] | DVERSTORP B, ANDERSSON J. Application of the discrete fracture network concept with field data: possibilities of model calibration and validation[J]. Water Resources Research, 1989, 25 (3) : 540-550 DOI:10.1029/WR025i003p00540 |
| [42] | TSANG Y W, TSANG C F, HALE F V, et al. Tracer transport in a stochastic continuum model of fractured media[J]. Water Resources Research, 1996, 32 (10) : 3077-3092 DOI:10.1029/96WR01397 |
| [43] | DE DREUZY J R, DAVY P, BOUR O. Hydraulic properties of two-dimensional random fracture networks following a power law length distribution: 2. permeability of networks based on lognormal distribution of apertures[J]. Water Resources Research, 2001, 37 (8) : 2079-2095 DOI:10.1029/2001WR900010 |
| [44] | DE DREUZY J R, DAVY P, BOUR O. Hydraulic properties of two-dimensional random fracture networks following a power law length distribution: 1. effective connectivity[J]. Water Resources Research, 2001, 37 (8) : 2065-2078 DOI:10.1029/2001WR900011 |




