2. 中铁大桥勘测设计院有限公司, 湖北 武汉 430050;
3. 中铁大桥(南京)桥隧诊治有限公司, 江苏 南京 210061
2. China Zhongtie Major Bridge Reconnaissance and Design Institute Co LTD, Wuhan 430050, Hubei, China;
3. China Zhongtie Major Bridge (Nanjing) Bridge and Tunnel Detecting and Treatment Co LTD, Nanjing 210061, Jiangsu, China
斜拉桥主梁的施工方法与梁式桥类似, 大体可以分为四种形式:平转法、顶推法、悬臂法和支架法, 支架法是目前斜拉桥主梁施工的主要方法之一。支架法施工简单, 能够确保结构设计满足线型的要求[1], 非常适用于搭设支架后不影响桥下交通的情况。石程华、李建刚通过建立满堂支架有限元模型, 基于实测结果, 分析验证了满堂支架在预压试验和混凝土浇筑等施工阶段的应力应变状态, 并提出了相应的施工监测方法[2]。LOZANO-GALANT J A等人基于正装分析提出了前向算法(forward algorithm, FA)应用于临时支架搭设方法的数值计算[3]。苏卫国、郑文通等人研究分析了支架受力行为及剪力撑屈服破坏的应力极限, 给出了支架受力最不利区域[4]; 刘东海等人对复杂地形条件下满堂支架的施工要点进行了分析[5]。
斜拉桥由于合理地利用梁、塔和高强度斜拉索各自的材料和力学特点, 在跨越大的障碍或河流时常作为优先桥型之一[6-7]。随着科学技术的发展, 斜拉桥塔梁施工新方法也越来越多, 其中“塔梁同步”施工作为一种新的施工方法具有明显优点:缩短工期, 节约成本, 方案经济。目前对塔梁同步施工的研究已比较多, 张拥军等人对满堂支架法塔梁同步施工监控内容及方法做了分析研究[8]; 张淑坤等人对大跨度悬臂法塔梁同步施工的影响因素及相应施工控制方法做了一一分析, 得出了主要影响因素与次要影响因素[9]; 刘爱林、王剑峰结合安庆长江铁路大桥, 对塔梁同步施工的关键施工技术及桥塔线型控制技术进行了研究[10]。
斜拉桥塔梁同步施工过程中, 在主塔尚未封顶之前就要进行斜拉索挂索及张拉, 因此对主塔两侧索力均等及塔偏偏位有较高要求。顾箭锋、曾祥红采用Midas/Civil有限元软件建立斜拉桥有限元模型, 利用影响矩阵法计算其合理成桥索力、合理施工索力, 分析了塔梁同步施工过程塔顶偏位的计算值[11]; 张文献等人通过建立某桥的有限元分析模型, 提出了利用综合法计算成桥索力的方法[12]; 赵玲等人通过建立斜拉桥的修正模型, 提出了综合运用斜拉桥竖弯振型频率变化、主梁模态曲率变化以及拉索索力变化进行拉索损伤位置识别的实用方法[13]; 蓝其平、陈景平对塔梁同步施工测量技术进行研究与分析, 得出塔梁同步施工中塔柱因受不均匀水平力产生塔柱偏移的修正方法[14]。
目前, 塔梁同步施工中考虑满堂支架分段拆除对斜拉桥结构力学特性影响的研究很少, 本研究参照文献[15-19]中有关斜拉桥及连续刚构桥结构受力特性的有限元分析方法, 以邹城斜拉桥为施工背景, 利用Midas/Civil有限元软件对该桥施工过程的结构受力进行了数值仿真计算, 对比计算结果与现场实测数据, 重点研究了满堂支架分段拆除的塔梁同步施工过程对斜拉桥主梁、主塔上、下塔柱和斜拉索等结构力学性能的影响。邹城斜拉桥于2015-04-10桥面铺装完成, 主桥线型及结构受力均满足设计要求, 计算分析及实测结果表明:满堂支架分段拆除的塔梁同步施工不仅能保证斜拉桥有良好的力学性能、施工质量, 还能明显缩短施工工期、降低工程造价, 为同类型的斜拉桥施工提供参考。
1 工程背景邹城斜拉桥为独塔双柱双跨双索面预应力混凝土斜拉桥, 墩塔梁固结体系, 跨越京沪铁路和站场线路及规划的电厂专用线, 共跨越14股道。斜拉桥布置图如图 1所示。
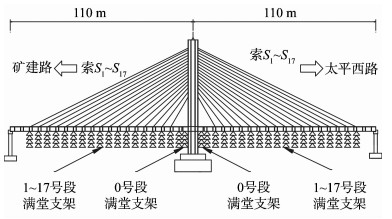
|
图 1 邹城斜拉桥布置及斜拉索、满堂支架编号 Figure 1 The stay-cables number and the full scaffold number of Zoucheng cable-stayed bridge 注: 1~17号段支架编号与索号S1~S17沿主梁纵向位置一一对应。 |
主桥跨径组合为110.0 m+110.0 m, 主塔为双柱钢筋混凝土结构, 塔高为51.6 m; 截面为箱形, 顺桥向宽6.0 m, 横桥向宽3.0 m; 主墩采用实体墩, 做矩形槽挖空; 全桥共34对(68根)平行钢丝束斜拉索, 索面呈扇形布置, 索力采用二次张拉方式; 邹城斜拉桥为转体斜拉桥, 转体质量21 000 t, 转体角度97°, 转体长度99.0 m+99.0 m, 转盘采用球面直径8.0 m的球铰转盘, 平面投影直径4.2 m, 分上下两片, 钢板厚度均为5.5 cm。
主梁采用纵、横、竖三向预应力体系。纵、横向预应力张拉控制应力均为1 302 MPa。梁索锚固区竖向预应力采用JL32精轧螺纹粗钢筋及YGM-32锚具, 预应力管道采用Φ50金属铁皮管。邹城斜拉桥施工实景如图 2所示。

|
图 2 施工实景 Figure 2 Live-action of construction |
因受施工工期的影响, 鉴于现场地形、施工组织、施工条件满足要求, 邹城斜拉桥施工采用塔梁同步施工、同时考虑满堂支架分段拆除的施工方案, 施工方案由原设计施工(工法一)改为实际施工(工法二), 如表 1所示。表 1中主梁0号块、1号块、2号块分别距离主梁中心0~10.0 m、10.0~51.5 m, 51.5~99.0 m; 主塔第一段、第二段、第三段分别位于梁顶面以上0~22.0 m、22.0~42.0 m、42.0~51.6 m。工法一中主塔、主梁、斜拉索、满堂支架拆除各工况分别施工, 施工工期分明; 工法二中主塔、主梁、斜拉索、满堂支架同步交错施工。
| 表 1 部分主桥施工方案 Table 1 Some construction stages of the bridge construction |
工法一与工法二的施工工期对比分析如表 2所示。由表中可看出, 工法二塔梁同步施工工期缩减了29 d, 为该桥后期转体时间的选择创造了更大的空间, 更重要的是能够保证该桥转体后在合适的大气温度下合龙。
| 表 2 上部结构施工时间对比 Table 2 Comparison of the construction times of the upper-structure |
邹城斜拉桥有限元计算模型如图 3所示。采用Madis/Civil软件进行数值计算, 模型中共有359个节点, 331个单元, 其中斜拉索只受拉单元34个, 并应用弹性连接的受压类型模拟满堂支架, 建立弹性连接单元54个。模型中考虑预应力荷载, 张拉应力为1 302 MPa, 考虑了5种预应力钢束类型, 41类预应力钢束形状, 在主梁施工工况中考虑了预应力张拉工况。结合现场实测数据, 分析该施工过程中斜拉索、满堂支架、主塔的受力情况及主梁的线型变化。

|
图 3 邹城斜拉桥有限元模型 Figure 3 Finite element model of the Zoucheng cable-stayed bridge |
斜拉索挂索、张拉过程复杂且历时较长, 施工期间昼夜温度变化、施工顺序、施工人员技术水平等因素都会对斜拉索索力造成影响[20]。依据表 1中工法二的施工方案, 邹城斜拉桥斜拉索S1~S7初拉完成后, 主梁0号段满堂支架拆除, S13~S17索依次初张完成后, 主梁1~7号段满堂支架依次逐步拆除, 因此在邹城斜拉桥施工中需加强对斜拉索索力的控制, 既要保证主塔两侧张拉索力均等, 还要时刻关注满堂支架拆除过程中斜拉索索力变化值(CFC), 严格控制好施工的安全。
斜拉索初次张拉索力模型计算值与施工张拉后的实测值如表 3所示。表 3中索力实测值为单侧两根索初张索力的平均值。由表 3可知, 经对比分析, 斜拉索初张索力模型计算值与施工实测值相吻合。
| 表 3 斜拉索初张索力 Table 3 Initial tension force of cable |
斜拉索张拉过程中考虑现场满堂支架分节段拆除, 0号段满堂支架拆除前后S1~S7索力变化情况如图 4所示, 1~7号段满堂支架拆除前后索S1~S17索力变化情况如图 5所示。
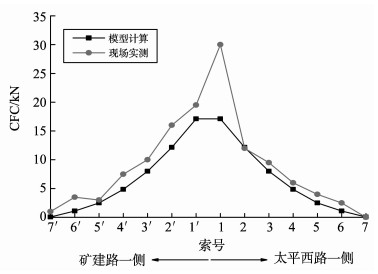
|
图 4 主梁0号段支架拆除前后索力变化 Figure 4 The cable force changes before and after the remove of the No.0 segment full scaffold |
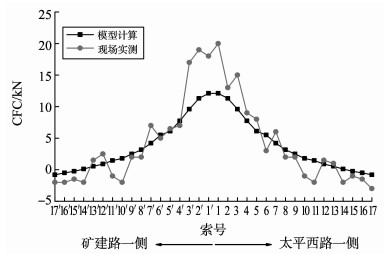
|
图 5 主梁1~7号段支架拆除前后索力变化 Figure 5 The cable force changes before and after the remove of the No.1~7 segment full scaffold |
图 4中索S1的模型计算最大索力变化值为17.1 kN, 占该索索力的0.96%;实测最大变化为30.0 kN, 占该索索力的1.67%。图 5中索S1的模型计算最大索力变化值为12.1 kN, 占该索索力的0.70%;实测最大变化值为20.0 kN, 占该索索力的1.16%。同时, 考虑斜拉索的拉索面积, 斜拉索S8的应力最大, 模型计算值为605.8 MPa, 实测值为610.1 MPa, 斜拉索材料的设计应力为1 670 MPa, 对应的安全系数模型计算值是2.76, 实测值是2.74, 均满足施工期索力2.5倍安全系数的要求。且由图 4、5可知, 斜拉索索力模型计算变化值与施工实测变化值相吻合, 有限元模型计算结果可靠。
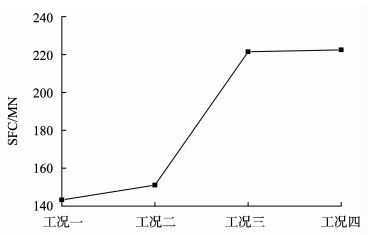
3.2 满堂支架、主墩支反力主桥施工过程中, 满堂支架受力及结构的合理性直接关系到主梁的施工质量和安全稳定。应用有限元软件Midas/Civil建模计算, 分析了满堂支架0号段拆除, 对1~17号段支架的影响; 以及1~7号段支架拆除, 对8~17号段支架的影响。0号段满堂支架拆除前后1~17号段满堂支架受力变化(FFC)情况如图 6所示; 0号段满堂支架拆除前后(工况一、工况二), 1~7号段满堂支架拆除前后(工况三、工况四)主墩永久支反力的变化(SFC)情况如图 7所示。
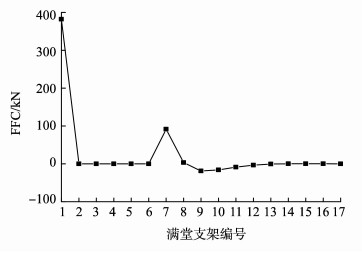
|
图 6 1~17号段满堂支架支反力大小变化 Figure 6 The support force changes of the No.1~17 segment full scaffold |
|
图 7 各施工工况下主墩永久支反力 Figure 7 The permanent support force changes under the construction stages |
经由Midas/Civil模型计算, 当索S1~S7依次分别张拉完成后, 1~6号支架支反力值依次变为0(即支架与底模脱离), 此时7号支架仍存在支反力, 其值明显减小, 仅为斜拉索张拉前支反力的17.16%。由图 6可知, 0号段支架拆除, 1号支架支反力变化值最大为382 kN, 2~7段支架支反力变化值不大, 均在100 kN以内。且经模型计算, 当索S8~S17依次分别张拉完成后, 7~17号支架支反力值依次变为0, 此时梁底与支架已全部脱离, 支架拆除对主桥受力已没有影响。由图 7可知, 主墩支反力随各施工工况的进行逐渐增大。
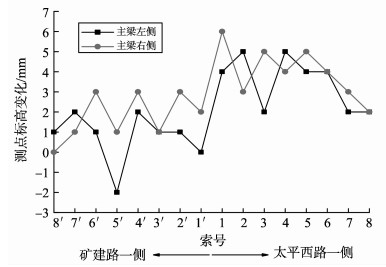
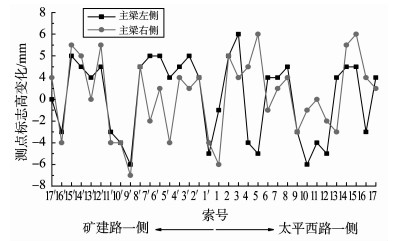
3.3 主桥线型斜拉桥采用的施工方法属于分段施工, 随着施工过程的进行, 桥梁结构各施工工况下的线型在不断发生变化。Midas/Civil模型计算结果显示, 0号段、1~7号段支架拆除前后, 主梁线型最大变化值为0.6 mm, 几乎没有变化, 因此不做分析。现场0号段、1~7号段支架拆除前后主梁线型测点标高变化值如图 8、9所示。图 8、9中主梁线型测点编号与索S1~S17编号沿主梁纵向位置一一对应。
|
图 8 0号段支架拆除前后主梁实测线型变化 Figure 8 The measured linear changes before and after the No.0 segment full scaffold |
|
图 9 1~7号段支架拆除前后主梁实测线型变化 Figure 9 The measured linear changes before and after the demolition of the No.1-7 segment full scaffold |
主梁线型测量使用莱卡NA730水准仪, 每km高程往返测精度1.2 mm, 且实际测量过程测量人员固定, 测试时间为清晨, 测量数据可靠。图 8中0号段支架拆除前后主梁实测线型最大变化值为6 mm, 图 9中1~7号段支架拆除前后主梁实测线型最大变化值为-7 mm, 主梁线型变化不大。
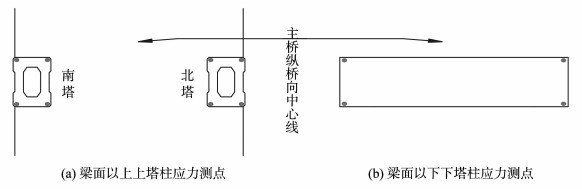
3.4 塔梁固结处应力采用塔梁同步施工技术的斜拉桥, 其施工控制目标与普通斜拉桥无异, 即达到所谓的合理成桥状态, 同时确保施工过程中桥梁结构的安全。邹城斜拉桥在主塔第三阶段尚未施工完成时, 就考虑0号段满堂支架拆除。理论分析可知, 塔梁固结处的压应力储备较小, 现场在主塔浇筑前, 预先在塔梁固结处布设应力测点。具体为取主塔塔梁固结处梁面以上1 m位置及梁底以下1 m位置两个应力测试断面, 断面位置应力测点平面分布如图 10所示。
|
图 10 主塔应力测点平面分布图 Figure 10 Plane distribution of stress measurement points of main tower 注:图中圆点表示应力传感器布设位置。 |
对0号段满堂支架拆除前、后, 1~7号段满堂支架拆除前、后四个工况进行分析, 模型应力计算结果与现场施工后应力实测结果如表 4所示。表 4中各工况下的应力实测值为每个断面应力测试值的平均值。
| 表 4 塔梁固结处应力 Table 4 The stress in the consolidation position betweenthe beam and the tower |
从表 4可以看出, 以上各施工工况下塔梁固结处应力均处于压应力状态, 0号段支架、1~7号段支架拆除后压应力相比拆除前略有增大, 最大变化值为-0.3 MPa, 主塔结构受力安全。
4 结论(1) 通过有限元计算结果, 满堂支架0号段拆除后, 1号段支反力增大382 kN, 支反力较拆除前增大18.5%, 建议现场支架预压时相应节段考虑一定安全系数, 同时施工过程中加强监测力度。
(2) 斜拉桥满堂支架全部拆除, 体系转换完成后要切实做好斜拉索索力及主梁挠度变化监测, 确保主塔两侧受力均衡。主墩受力一直增大且考虑到全桥转体尚未封铰, 易受外部因素影响, 要进行临时锁定。
(3) 本研究证实了满堂支架分段拆除塔梁同步施工方案可行性, 可为主桥转体前结构受力状态提供参考。同时, 考虑到主桥转体过程中影响参数更多, 可进一步开展转体过程中外部因素(如风荷载等)影响下主梁、主塔和斜拉索力学特性研究。
| [1] |
游朝辉, 魏星. 支架法施工斜拉桥主梁线性控制[J].
科技与企业, 2013 (21) : 202 YOU Chaohui, WEI Xing. Linear control of main girder of cable stayed bridge with full scaffold method[J]. Science-Technology Enterprise, 2013 (21) : 202 |
| [2] |
石程华. 现浇箱梁碗扣式满堂支架整体计算分析与监测技术研究[J].
公路, 2015 (7) : 156-160 SHI Chenghua. Study on the integral calculation analysis and monitoring technology of cast-in-situ box girder bowlfull scaffold construction[J]. Highway, 2015 (7) : 156-160 |
| [3] | LOZANO-GALANT J A, PAYA-ZAFORTEZA I, XU D, et al. Forward Algorithm for the construction control of cable-stayed bridges built on temporary supports[J]. Engineering Structures, 2012, 40 (7) : 119-130 |
| [4] |
苏卫国, 刘剑. 现浇箱梁高支模满堂支架的有限元分析[J].
华南理工大学学报(自然科学版), 2013, 41 (2) : 82-87 SU Weiguo, LIU Jian. Finite element analysis of cast-in-situ box girder bowlfull scaffold[J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41 (2) : 82-87 |
| [5] |
刘东海, 杨健, 方军. 复杂地形条件下满堂支架法现浇箱梁的应用[J].
公路交通科技(应用技术版), 2013 (11) : 362-365 LIU Donghai, YANG Jian, FANG Jun. The application of bowlfull scaffold method of cast-in-place box girder under the complex terrain condition[J]. Journal of Highway Traffic Science and Technology (Application Technology), 2013 (11) : 362-365 |
| [6] | 徐君兰. 大跨度桥梁施工控制[M]. 北京: 人民交通出版社, 2000 . |
| [7] | 向中富. 桥梁施工控制技术[M]. 北京: 人民交通出版社, 2001 . |
| [8] |
张拥军, 蒋卫东. 超宽斜拉桥塔梁同步施工方案与控制技术[J].
公路交通科技(应用技术版), 2009 (5) : 172-175 ZHANG Yongjun, JIANG Weidong. Synchronous construction scheme and control technology of tower beam of super-breadth cable-stayed bridge[J]. Journal of Highway Traffic Science and Technology (Application Technology), 2009 (5) : 172-175 |
| [9] |
张淑坤, 张向东, 陆启珂. 大跨度斜拉桥塔梁同步施工控制技术[J].
广西大学学报(自然科学版), 2012, 37 (1) : 88-93 ZHANG Shukun, ZHANG Xiangdong, LU Qike. Research on the construction control technology of large span cable-stayed bridge tower and girder[J]. Journal of Guangxi University (Natural Science Edition), 2012, 37 (1) : 88-93 |
| [10] |
刘爱林, 王剑峰. 安庆长江铁路大桥主桥桥塔施工关键技术[J].
桥梁建设, 2013, 43 (3) : 31-36 LIU Ailin, WANG Jianfeng. Key techniques for construction of pylons of main bridge of anqing changjiang river railway bridge[J]. Bridge Construction, 2013, 43 (3) : 31-36 |
| [11] |
顾箭峰, 曾祥红. 混合梁斜拉桥塔梁同步施工可行性分析[J].
桥梁建设, 2016, 46 (1) : 111-116 GU Jianfeng, ZENG Xianghong. Feasibility analysis of synchronous construction of pylon and main girder of hybird girder cable-stayed bridge[J]. Bridge Construction, 2016, 46 (1) : 111-116 |
| [12] |
张文献, 刘旭光, 李东炜, 等. 斜拉桥成桥及施工阶段的索力优化[J].
东北大学学报(自然科学版), 2009, 30 (8) : 1201-1204 ZHANG Wenxian, LIU Xuguang, LI Dongwei, et al. Optimizing cable tension during construction and completion of a cable-stayed bridge[J]. Journal of Northeastern University (Natural Science), 2009, 30 (8) : 1201-1204 |
| [13] |
赵玲, 李爱群, 缪长青, 等. 大跨斜拉桥的拉索损伤识别[J].
桥梁建设, 2004 (5) : 19-22 ZHAO Ling, LI Aiqun, MIU Changqing, et al. Identification of damages in stay cables of long-span cable-stayed bridges[J]. Bridge Construction, 2004 (5) : 19-22 |
| [14] |
蓝其平, 陈景平. 关于斜拉桥塔梁同步施工测量技术的研究[J].
测绘通报, 2011 (9) : 48-51 LAN Qiping, CHEN Jingping. On simultaneous construction survey technique for beam tower of cable-stayed bridge[J]. Bulletin of Surveying and Mapping, 2011 (9) : 48-51 |
| [15] |
王立峰, 王二强, 孙永存, 等. 万吨级斜拉桥转体施工过程的力学特性[J].
交通运输工程学报, 2015, 15 (3) : 52-61 WANG Lifeng, WANG Erqiang, SUN Yongcun, et al. Mechanical properties of ten thousand-ton class cable-stayed bridge in rotation construction process[J]. Journal of Traffic and Transportation Engineering, 2015, 15 (3) : 52-61 |
| [16] | PEDRO J J O, REIS A J. Nonlinear analysis of composite steelconcrete cable-stayed bridges[J]. Engineering Structures, 2010, 32 : 2702-2716 DOI:10.1016/j.engstruct.2010.04.041 |
| [17] | NADERIAN H, CHEUNG M M S, SHEN Z Y, et al. Integrated finite strip analysis for long-span cable-stayed bridges[J]. Computers and Structures, 2015, 158 : 82-97 DOI:10.1016/j.compstruc.2015.05.031 |
| [18] |
徐向峰, 赵香萍, 张峰, 等. 重载铁路连续刚构桥徐变精细化数值分析[J].
山东大学学报(工学版), 2015, 45 (4) : 69-74 XU Xiangfeng, ZHAO Xiangping, ZHANG Feng, et al. Refined analysis of creep effect for heavy haul railway continuous rigid frame bridge[J]. Journal of Shandong University (Engineering Science), 2015, 45 (4) : 69-74 |
| [19] |
王海源, 章龙, 张乐文, 等. 预防连续箱梁施工裂缝的温度监测与有限元分析[J].
山东大学学报(工学版), 2011, 41 (3) : 82-88 WANG Haiyuan, ZHANG Long, ZHANG Lewen, et al. Temperature monitoring and finite element analysis of preventing construction cracks in a continuous box girder[J]. Journal of Shandong University (Engineering Science), 2011, 41 (3) : 82-88 |
| [20] |
李小珍, 蔡婧, 强士中. 大跨度钢箱梁斜拉桥索梁锚固结构型式的比较研究[J].
土木工程学报, 2004, 37 (3) : 73-79 LI Xiaozhen, CAI Jing, QIANG Shizhong. Studies on models of cable-girder anchorage for long-span cable-stayed bridges with steel box girder[J]. China Civil Engineering Journal, 2004, 37 (3) : 73-79 |




