2. 中国科学院岩土力学研究所, 湖北 武汉 430000;
3. 广西新发展交通集团有限公司, 广西 南宁 530029;
4. 桂林理工大学土木与建筑工程学院, 广西 桂林 541004;
5. 广西大学土木与建筑工程学院,广西 南宁 530004;
6. 交通运输部公路科学研究院, 北京 100088
2. Institute Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430000, Hubei, China ;
3. Guangxi Xinfazhan Communications Group, Nanning 530029, Guangxi, China ;
4. College of Civil Engineering and Architecture, Guilin University of Technology, Guilin 541004, Guangxi, China ;
5. College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, Guangxi, China ;
6. Research Institute of Highway Ministry of Transport, Beijing 100088, China
我国高速公路通车里程世界第一, 其中绝大部分是沥青路面, 对道路进行科学养护和管理是道路大建设以后的重要任务。 借助力学手段揭示路面病害产生机理, 并提出有效的病害防治技术, 是养护工作的重中之重, 具有重要的工程和社会意义。
当前世界各国众多的沥青路面设计方法主要分为两类:一是以经验或试验为依据的经验法;二是以力学分析为基础, 考虑环境、交通条件以及材料特性为依据的力学经验法。 经验法重在试验, 适应于新建道路, 而旧路改造就很难使用;车辆荷载不同, 不同地方的气候环境、水文地质不同, 在各地大量修建试验路进行大量的试验, 其费用非常昂贵, 难以承担;同时经验法对新材料的应用很难适应, 对具体材料的实际性能很难较好地利用;对路面性能的预测也不够准确。 但该方法在现代路面发展初期作为路面设计的一种过渡方法, 却是一种很好很成熟的方法。 近年来随着交通量的增加、气候条件的改变和新型材料的发展等, 力学经验的分析法悄然兴起。 这种力学分析方法, 采用结构分析的理论和计算方法, 建立多维的有限元模型, 综合考虑荷载、材料、气候和地质等因素的影响, 确保路面既经济又安全地在服务期限内发挥较好的使用性能。 壳牌(SHELL)沥青路面设计方法、美国AASHTO力学经验法设计指南及德国累斯顿工业大学路面设计研究所一直以来研究的Dresden模型均属于这种方法。
目前我国路面主要利用层状弹性体系理论进行设计, 这种理论对新建路面的力学分析是适用的。 但是, 路面病害的力学机理非常复杂, 涉及到多种力学理论, 层状弹性体系理论远不能满足工程要求, 需要建立路面病害力学理论体系。 例如, 为了更好地预测全寿命周期内沥青路面的弯沉和变形, 需要借助弹塑性和黏弹性力学;路面开裂分析需借助断裂力学和损伤力学;复杂的水损坏分析需借助流固耦合力学分析;道路翻浆需借助多物理场分析;路面磨损需借助摩擦与磨损力学进行分析。 为此, 本研究从破坏力学的角度, 对沥青路面几种主要病害的力学机理进行了概括性分析, 对国内外与路面病害有关的力学研究进行了简要论述, 希望对路面病害力学体系的建立起到一定的指导作用。
1 常温下路面的塑性变形 1.1 常用道路材料塑性本构模型本构模型的选取, 主要遵循以下两个原则:
(1) 材料模型要尽量符合实际情况。
(2) 材料模型要尽量简单, 参数要少且容易获取。 一般情况下, 参数越多, 越不容易精确获得。 在参数测不准的情况下, 越多的参数反而会影响计算精度。
目前路面力学分析中应用最多的理想弹塑性模型是Tresca模型、Mises模型和Mohr-coulomb(M-C)模型, 其中M-C模型因为考虑了平均主应力的影响, 被广泛应用。 另外, 路面材料试验表明, 在应力达到峰值后应力会下降, 表现为应变软化现象, 所以应变软化模型应该更能反映实际情况。
应变软化是许多路面材料的本构特性。 应变软化主要有两类[1]:一类是非相关软化;另一类是考虑初始缺陷导致损伤演化而引起的材料软化。
第一类软化是因剪胀角与内摩擦角不等引起的。 对这种材料, 发生破坏的方向与材料流动的方向不一致, 即速度特征线与应力特征线不一致。 对θ=0的非相关材料, 速度特征线与最大主应力方向成45°角, 而应力特征线与最大主应力方向之间的夹角为π/4-θ/2。
第二类软化是在本构模型中考虑了材料的损伤演化。 在一些商用软件如FLAC3D中, 软化模型是由M-C模型修正而来的。 其通过定义c和φ随σi=k中Mises应力的增大而减小的规律曲线, 来表示损伤的演化和材料的软化。
以上两类软化模型理论上都会使材料内部形成剪切带, 并伴有软化现象发生。 但实际上对剪切带的模拟一般较难, 这要依赖于单元网格的划分。 网格划分得越细, 剪切带越容易形成。 所以, 模拟剪切带会耗费大量的机时, 这也是大多采用理想弹塑性模型来进行计算的原因。 若要研究开裂, 最有效的方法是借助于断裂力学和损伤力学等高等力学手段。
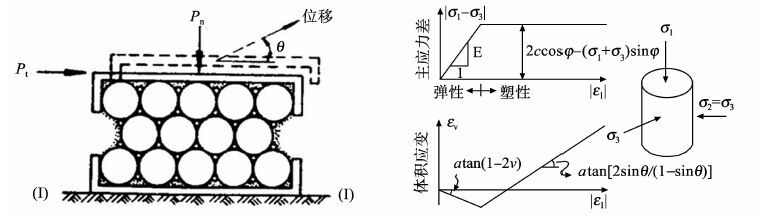
1.2 路面材料的剪胀一般情况下, 剪切变形往往伴随着体积增加, 这种特性叫做剪胀。 剪胀性可以通过图 1所示的简单物理模型进行说明[2]。 模型上作用着两个力, 一个是法向力Pn, 另一个是水平力Pt。 假设Pn保持常数, 而使Pt从零逐渐增加, 直至产生滑动。 在滑动瞬时, Pt不仅需要克服黏聚力, 而且还必须超过由两类摩擦引起的阻力。 第一类摩擦发生在相邻集料和细颗粒的接触面上, 叫做面摩擦;第二类摩擦是由集料和细颗粒本身阻止改变其相对位置所引起的, 叫咬合摩擦。 这种咬合摩擦除了引起侧向位移外, 还可引起向上的位移。 因此, 位移向量必会与滑动面成一个角度θ, 称为剪胀角。
|
图 1 剪胀的物理模型 Figure 1 Physical model of shear dilatation |
沥青路面永久性变形, 包括路面弯沉、车辙等, 是沥青路面主要病害之一。 在过去的十几年中, 道路交通量急剧增加, 尤其是大型重载卡车数量越来越多, 重型车辆荷载反复作用导致道路永久变形病害发生时间越来越早, 进行路面塑性变形分析具有重要意义。
元松等利用动力有限元计算并分析了柔性路面结构在落锤式弯沉仪(falling weight deflectionmeters, FWD)作用下的动力响应特性, 发现随路面强度增加, 路面对荷载的扩散能力逐渐增强, 同时中央弯沉峰值减小, 其中面层强度对弯沉峰值影响最为明显, 另外面层强度越大, 弯沉盆面积越大[3]。 郑元勋和杨培冰改变沥青路面温度, 建立有限元热-结构耦合模型[4]。 研究发现, 在FWD动态加载下路面温度对路面动态弯沉尤其是最大弯沉值影响较为显著;温度一定时, 弯沉随路面厚度增加呈逐渐减小趋势;而随温度增高, 路面厚度对弯沉的影响逐渐减小。 黄磊等采用BISAR软件模拟在FWD作用下道路各结构层参数对路面弯沉的影响, 结果显示土基模量影响最为显著[5]。 赵杏梅通过模型试验表明, 增大车辆轴重会使基层顶部竖向应变、路表弯沉显著增大, 加速路面的破坏, 因此应控制重载和超载车辆比例;车速越大, 各响应值越小, 对沥青路面的破坏越小;增大中面层模量能显著减小路表弯沉;增大基层模量能有效减小路表弯沉和基层顶部竖向压应变[6]。 刘宇星等建立了沥青路面层状半空间弹塑性模型, 通过ANSYS瞬态动力分析模拟小球贯入试验, 并采用动态设计参数(动态模量)得到了冲击荷载作用下沥青路表面的塑性变形规律, 同时验证了理论计算结果和材料参数的合理性[7]。 郑健龙通过大量交通量调查和路表弯沉检测, 建立了沥青路面容许弯沉与累计交通量的幂函数关系, 揭示了沥青路面相对弯沉变化规律[8]。
2 路面开裂的断裂与损伤力学模型沥青路面的裂缝有龟裂、反射裂缝、温度裂缝、路基不均匀沉降引起的裂缝等。 路面宏观的裂缝现象是路面结构在轴载和环境共同作用下力学行为的直接反映。 沥青路面暴露在自然环境和行车荷载的作用下, 加上前期施工因素的影响, 使许多沥青路面在竣工后1~2a内就出现了早期破坏, 因此开展路面开裂与损伤力学行为的研究是至关重要的。 随着力学领域中破坏理论研究的发展, 关于沥青路面结构开裂破坏的研究有了很大发展。
2.1 沥青材料疲劳破坏分析方法沥青路面受到反复的交通荷载, 疲劳破坏是路面的主要破坏形式。 沥青材料疲劳破坏分析主要有以下4种方法。
(1) 现象学法
现象学法主要是通过试验将疲劳寿命与所施加应变(或应力)、材料劲度及材料或环境参数等建立关系, 提出经验型的疲劳寿命模型。 常用的有一下三种模型。
① 疲劳寿命-应变模型
根据疲劳试验结果, 沥青混合材料疲劳寿命和应变的关系通常用下式进行表述:
| ${{N}_{f}}={{({{\varepsilon }_{t}})}^{-n}}, $ | (1) |
式中, Nf为疲劳破坏时荷载的重复作用次数;εt为拉应变;k、n为与材料性质和试验条件有关的回归系数。
② 疲劳寿命-应变-劲度模型
由于沥青混合材料是黏弹性材料, 其劲度模量随温度和荷载作用时间的不同而发生变化。 研究表明, 混合料的劲度和疲劳寿命有较强的相关性。
MONISMITH C L 和SALAM Y M建立了包含混合料劲度的疲劳模型[9]:
| ${{N}_{f}}=k{{(\varepsilon t)}^{-n}}{{(Smix)}^{-m}}, $ | (2) |
式中, Nf为疲劳破坏时荷载的重复作用次数;εt为沥青层底部拉应变;Smix为沥青混合料劲度模量;k、n为与材料性质和试验条件有关的回归系数。
③ 疲劳寿命-应变-材料和环境参数模型
为了提高疲劳模型的适用性, 对不同类型沥青混合料开展不同试验环境下的疲劳试验, 建立了包含材料参数的疲劳寿命预测模型。 不同学者提出了不同的疲劳寿命-应变-材料和环境参数模型。
现象学方法具有简便直观, 可直接应用于路面疲劳寿命设计的优点, 但疲劳寿命只与初始试验条件有关, 且试验方法不统一。
(2) 能耗模型
自滞回能与疲劳特性的关系被提出以来, 人们逐渐注意到疲劳损伤的产生、累积以及疲劳破坏都与疲劳过程中的能量吸收与累积有关。 疲劳过程中观察到的Bauschinger效应和迟滞现象都证明了这个过程中耗散的能量。 因此, 人们自然而然地希望能用能量的累积来描述材料的损伤过程。 能量耗散与损伤演化的密切关系使得这种描述具有明确的物理意义, 同时能量作为标量的可加性使得这种描述更具简捷性。 随着疲劳试验方法和测试技术的完善, 人们能够精确地测量疲劳过程中能量的耗散, 这为疲劳能量理论的发展奠定了试验基础。
1972年VAN DIJK W和MOREAUD H等首先将能耗的概念用于分析沥青膜的疲劳问题[10], 并将能量的概念扩展到沥青混合料的疲劳分析中, 其后许多研究者都采用“能量法”研究过沥青混合料的疲劳特性。 其基本思想是将沥青混合料的疲劳寿命与失效前的累积耗散能相关联:
| $WN=A{{(Nf)}^{z}}, $ | (3) |
式中, Nf为疲劳寿命;WN为疲劳屈服前的累积耗散能;A、z为由试验数据拟合得到的常数。
总体来说, 能量方法的优点是疲劳寿命与试验方法无关, 但其缺点就是未能考虑疲劳破坏发展过程。
(3) 断裂力学分析方法
基于结构内部存在裂缝类缺陷的断裂力学理论与方法在沥青类路面工程中的应用, 至今为止依次经历了线弹性断裂力学、疲劳断裂力学与黏弹性断裂力学等几类断裂力学理论与方法。 由于沥青类路面结构始终处在交通荷载和温度荷载的循环作用下, 其破坏主要表现为疲劳破坏特征。 因此, 目前关于沥青类路面结构的开裂研究主要集中在疲劳断裂力学理论与方法的应用。 在应用严格意义上的疲劳断裂力学理论与方法时, 人们普遍采用基于应力强度因子的Paris经验性方程, 描述沥青类路面疲劳裂缝扩展过程, 并以此计算疲劳裂缝扩展寿命。 根据理论分析结果和疲劳断裂试验数据, 提出沥青类路面结构的使用寿命预测方法。 由于沥青材料具有较强的温度敏感性, 具有热黏弹性材料特征, 研究发现用Schapery理论研究沥青混合料及其结构的疲劳裂缝扩展过程比较准确。
(4) 损伤力学分析方法
目前很多学者利用损伤力学开展了沥青路面破坏分析, 提出了一些工程上可行的模型和方法, 其中Miner疲劳损伤线性累积模型已经被广泛用来预测沥青路面的疲劳寿命。 损伤力学与断裂力学一起组成路面破坏力学的主要框架, 以研究路面由损伤直至断裂破坏的力学规律。 下面将简要论述沥青路面断裂力学和损伤力学分析方法和模型。
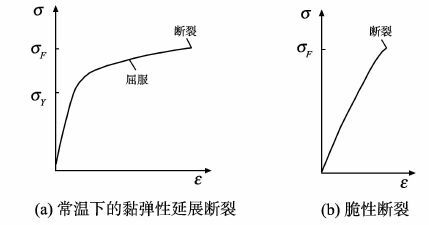
2.2 基于断裂力学的沥青材料开裂行为与力学模型 2.2.1 沥青材料开裂行为在不同环境下, 沥青材料的开裂表现为图 2所示的两种不同的行为[11]:(1) 常温下沥青材料发生的黏弹性断裂;(2) 低温下沥青材料发生的脆性断裂。 一般来讲, 在沥青材料发生断裂之前, 处于材料极限应变范围内的大多为弹性形变。 对于常温下沥青材料发生的延展黏弹性断裂, 是指当材料超过强度σY发生断裂, 在裂纹尖端的塑性区发生塑性变形的行为。 在这种情况下, 最终断裂时的极限应力将会在材料产生足够大的非弹性形变后产生。 对于低温下沥青材料发生的脆性断裂, 在断裂前将不会发生明显的非弹性形变。
|
图 2 沥青材料的断裂力学行为 Figure 2 Fracture mechanics behavior of asphalt material |
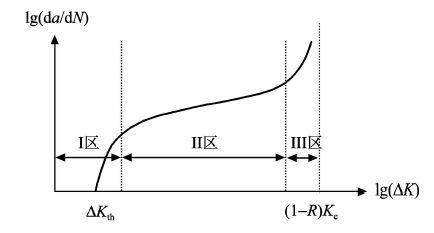
作为沥青路面破坏的主要形式之一, 疲劳断裂是道路工作者关注的焦点问题之一。 一般认为沥青路面发生疲劳断裂的主要原因是路面内的微缺陷在循环荷载作用下出现了微裂纹生长, 并最终导致宏观裂缝而发生破坏。 需要注意的是, 该阶段的“裂纹生长”是分阶段逐步进行的, 结构的破坏正是由于其内部存在的缺陷引起的应力集中与内部损伤, 当这种应力集中与损伤积累超过材料与结构抵抗破坏的容许值时, 就引起内部缺陷的发展, 并导致结构的破坏。 总地来说, 疲劳破坏可以分为图 3所示的3个阶段。
(1) 第Ⅰ阶段(Ⅰ区):存在一个门槛应力强度因子幅 ΔKth, 当应力强度因子范围低于门槛值时, 即 ΔK≤ΔKth时, 疲劳裂纹基本不扩展。 这个阶段为疲劳裂纹的萌生阶段, 由于疲劳裂纹萌生后的初始扩展阶段和裂纹的萌生阶段没有明显的界限, 区分起来比较困难, 因此把裂纹扩展的初始阶段也归入疲劳裂纹扩展的第Ⅰ阶段。
(2) 第Ⅱ阶段(Ⅱ区):为裂纹的稳定扩展阶段(亚临界扩展阶段), 此时应力强度因子范围大于 ΔKth。 在该区内, 裂纹扩展速率da/dN与应力强度因子幅服从下面要介绍的Paris方程, 所以也称Paris区。
(3) 第Ⅲ阶段(Ⅲ区):为裂纹快速扩展阶段, 此时da/dN很大, 疲劳裂纹扩展寿命短, 其对裂纹扩展寿命的贡献通常可以不考虑。 断裂发生条件是由Kmax <Kc所控制, 而由换算关系ΔK=(1-R)Kmax可知, 图 3的上渐近线为 ΔK=(1-R)Kc (Kc为材料的断裂韧性, R为荷载应力比)。
|
图 3 疲劳裂纹生长示意图 Figure 3 Schematic of the development of fatigue crack |
在实际工程应用中, 一般主要以第Ⅱ阶段作为疲劳裂纹扩展寿命的研究区域。
2.2.3 沥青路面疲劳断裂模型目前, 描述循环荷载作用下路面裂纹生长最常用的模型是由PARIS P C和ERDOGAN F A提出的, 即Paris方程(1963年)[12]:
| $\frac{da}{dN}=C{{(\Delta K)}^{m}}, $ | (4) |
式中, C和m都是材料疲劳性能参数, 需要由试验测出。
Paris公式的主要物理意义为基于相应的材料参数计算沥青材料在给定初始裂纹和循环荷载作用下的疲劳寿命。 当裂缝达到其临界长度ac时的应力荷载循环次数N就成为沥青疲劳寿命的主要指标。 考虑沥青试件受到循环应力强度因子
| $N\left( a \right)=\frac{1}{C{{(\Delta \sigma )}^{m}}}{{\int }_{a}}{{_{i}}^{a}}\frac{d\bar{a}}{{{[\sqrt{\pi \bar{a}}F(\bar{a})]}^{m}}}。$ | (5) |
MAJIDZADEH K和TALBERT L O是最早应用Paris方程, 利用工程断裂力学知识分析路面结构疲劳破坏现象的学者[13]。 他们在研究设有柔性界面层的路面裂缝疲劳问题时发现:有限元计算过程中为了达到足够的计算精度, 运用有限元方法计算路面裂缝尖端的应力强度因子时裂缝尖端的单元划分具有特殊性, 采用奇异单元划分后的计算结果较为精确。 对于这种情况, 他们提出了使用更多高次项的数学表达式来描述沥青混合料的疲劳开裂:
| $\frac{da}{dN}=AK+B{{K}^{2}}+C{{K}^{4}}+D{{K}^{6}}, $ | (6) |
式中A、B、C和D为材料断裂参数。
但是采用高次数学表达式时, 由于结构模型参数较多, 与实际道路系统的力学性能比较难相符, 因此MAJIDZADEH K和TALBERT L O又对模型进行了简化:
| $\frac{da}{dN}={{A}_{1}}{{K}^{2}}+{{A}_{2}}{{K}^{4}}, $ | (7) |
式中A1和A2为材料断裂参数。
简化模型经计算发现计算精度有所降低, 但是对于道路的设计计算却更加方便。 Paris方程得出的实际上是基于弹性材料得到的结果, 然而沥青混合料的力学行为具有明显的黏弹性特征, 多年的研究发现, 用Sehapery理论[14-16]来研究沥青及沥青混合料的黏弹性特性及其道路体系结构的疲劳裂缝扩展过程比较准确。 这一理论与Paris方程在形式上具有相似性, 可以利用此理论预测Paris方程中的C和m两个参数:
| $C=\frac{\pi }{6{{\sigma }_{m}}^{2}{{I}_{1}}^{2}}{{\left[ \text{ }\frac{\left( 1-{{\mu }^{2}} \right){{D}_{2}}}{2\Gamma } \right]}^{\frac{1}{n}}}\cdot \int_{_{0}}^{\Delta t}{w}{{\left( t \right)}^{m}}dt。$ | (8) |
对于控制位移试验:
| $m=2\left( 1+\frac{1}{n} \right)。$ | (9) |
对于控制应力试验:
| $m=\frac{2}{n}, $ | (10) |
以上各式中, I1为因子, 取决于裂尖应力条件、破坏应力和破坏区长度;D2为在时间t=1s时的柔量;μ是泊松比;Γ是断裂能量, 定义为形成单位裂纹表面面积所做的功;W(t)为应力强度因子的波形;n为拉伸蠕变柔量曲线的斜率;σm为最大拉伸强度;Δt为完成一次加载循环的加载周期。
后来, 研究者在此基础上, 经过采用不同试验方法对不同的沥青混合料开展疲劳断裂试验, 提出了用Schapery理论计算疲劳断裂参数的修正公式[17]。
JACOBS MM J提出了与试验测试结果吻合较好的另一种形式的参数[18]:
| $C={{10}^{d}}{{(\frac{1}{\sigma m})}^{a}}{{(\frac{1}{2{{\Gamma }_{stat}}})}^{\frac{b}{n}}}{{(\frac{1}{{{S}_{mas}}}1)}^{\frac{c}{n}}}, $ | (11) |
式中, Γstat为从静态(或半静态)试验中确定的断裂能量;Smas为由主曲线确定的混合料的刚度模量; a、b、c、d为回归系数。
JACOBS MM J通过大量沥青混合料的试验发现C和m遵从下列关系:
| $\text{lg}C=-2.36-1.14m。$ | (12) |
在实际工程问题中, 由于交通荷载的不对称、 路面结构的不对称或者裂纹方位的不对称以及材料的各向异性, 使裂纹经常以复合型的形式存在。 在复合型裂纹扩展速率的研究中, 由于Ⅱ型和Ⅲ型裂纹的存在, 使问题变得更为复杂。 含有Ⅱ型裂纹的情况往往改变原裂纹的扩展方向; 含有Ⅲ型裂纹的情况往往发生裂纹面的扭转。 一个常规的处理方法就是将各型裂纹对应的应力强度因子采用某种方式组合, 以有效应力强度因子ΔKeff作为控制参量来分析问题。 ROSITER J等通过三点弯拉试验, 提出了Ⅰ型与Ⅱ型并存的复合型开裂的广义Paris公式[19]:
| $\frac{da}{dN}=C{{(\Delta {{K}_{eff}})}^{m}}, $ | (13) |
式中:Keff为与ΔKⅠ和ΔKⅡ有关的有效应力强度因子:
| $\Delta {{K}_{eff}}={{(\Delta {{K}_{Ⅰ}}^{4}+3.5\Delta {{K}_{Ⅱ}}^{4})}^{0.25}}, $ | (14) |
| $C=\frac{3.53\times {{10}^{-6}}\Delta {{K}_{Ⅰ}}+4.67\times {{10}^{-3}}\Delta {{K}_{Ⅱ}}}{\Delta {{K}_{Ⅰ}}+\Delta {{K}_{Ⅱ}}}\times {{10}^{-3}}, $ | (15) |
| $m=\frac{3.5\Delta {{K}_{Ⅰ}}}{\Delta {{K}_{Ⅰ}}+\Delta {{K}_{Ⅱ}}}$ | (16) |
Paris方程由于其简便直观的特点, 在沥青疲劳性能预测方面获得了广泛应用。 但很多试验发现疲劳裂纹扩展速率受到平均应力或更普遍地认为受到应力比的影响, 有几种疲劳裂纹扩展速率模型考虑了应力比的影响, 较有名的有Forman方程[20]和Walker方程[21]。 Forman方程同时也将材料的断裂韧性Kc考虑为重要影响因素:
| $\frac{da}{dN}=\frac{C{{\left( \Delta K \right)}^{m}}}{\left( 1-R \right){{K}_{c}}-\Delta K}, $ | (17) |
式中, R=Kmin/Kmax, 称为应力比。
Walker方程也是工程中描述应力比对裂纹扩展速率影响的一个常用数学模型, 并且考虑了峰值载荷时的应力强度因子Kmax的影响:
| $\frac{da}{dN}=C{{[{{\left( 1-R \right)}^{m}}{{K}_{max}}]}^{n}}, $ | (18) |
式中C、m、n是由不同应力比下的疲劳裂纹扩展实验数据拟合得到的3个材料参数。
在疲劳断裂力学研究过程中, 一些学者对Paris方程做了进一步的修正, 对沥青路面的开裂有重要的借鉴意义。 ELBER W在平面应力试件拉—拉疲劳裂纹扩展试验中观察到裂纹闭合现象[22]。 只有当施加应力大于某一应力水平时, 裂纹才能完全张开, 此应力为裂纹张开应力;卸载时小于某一应力水平, 裂纹即开始闭合, 此应力为裂纹闭合应力。 试验证明张开应力与闭合应力大小基本相同。 根据他提出的裂纹闭合理论, 对Paris公式修正如下:
| $\frac{da}{dN}=C{{(\Delta {{K}_{eff}})}^{m}}=C{{\left( U\Delta K \right)}^{m}}={{U}^{m}}C{{\left( \Delta K \right)}^{m}}, $ | (19) |
式中, U为裂纹闭合参数, U=ΔKeff/ΔK=Δσeff/Δσ<1, 其中有效应力幅Δσeff为最大应力σmax与张开应力σop之差。
裂纹闭合理论对裂纹扩展加速和迟滞现象做出了初步解释, 对深入认识路面疲劳裂缝扩展的复杂机理十分有益。
由图 3可见, 只有当应力强度因子变化大于ΔKth时, 裂纹才会扩展。 为了考虑门槛应力强度因子幅ΔKth的影响, DONAHUE R J等对Paris公式做了如下修正[23]:
| $\frac{da}{dN}=C{{(\Delta K-\Delta {{K}_{th}})}^{m}}。$ | (20) |
而1977年, MCEVILY A J和GROEGER J在关于疲劳裂纹扩展门槛的研究中, 提出了如下方程(此时材料常数m=2) [24]:
| $\frac{da}{dN}=C{{(\Delta K-\Delta {{K}_{th}})}^{2}}(1+\frac{\Delta K}{{{K}_{c}}-{{K}_{max}}})。$ | (21) |
20世纪30年代, GRIFFITH首先提出在裂纹扩展过程中由于物体内部能量的释放所产生的裂纹驱动力导致了裂纹的增长, 这种裂纹驱动力称为能量释放率G, 与裂纹尺寸及外加荷载有关。
能量释放率G和应力强度因子K有直接关系, 对于Ⅰ、Ⅱ型裂纹有:
| $\left\{ \begin{matrix} G={{K}^{2}}E, \text{ }\left( 平面应变 \right); \\ G=\left( 1-{{\mu }^{2}} \right){{K}^{2}}E, \text{ }\left( 平面应变 \right) \\ \end{matrix} \right.$ | (22) |
对于Ⅲ型裂纹有:
| $G=(1+{{\mu }^{2}}){{K}^{2}}/E, $ | (23) |
以上各式中, E为弹性模量;μ为泊松比。
因此, 若求得能量释放率变化幅度ΔG, 则可把Paris方程用能量形式来表示:
| $\frac{da}{dN}=C{{\left( \Delta G \right)}^{m}}$ | (24) |
线弹性断裂力学给出的裂尖附近的应力趋于无穷大, 然而事实上任何实际工程材料, 都不可能承受无穷大的应力作用, 因此裂尖附近的材料必然要进入塑性, 发生屈服。 随着塑性变形量的增加, 裂尖塑性区增大, 疲劳裂纹扩展速率也不断增加, 再用ΔK来计算疲劳裂纹扩展速率往往会得出不安全的结论, 此时控制疲劳裂纹扩展的参量则宜用弹塑性断裂参量来描述。 弹塑性断裂力学中的一个主要问题是确定一个能定量表征裂纹尖端应力、应变场强度的参量, 其既易于计算出来, 又能通过试验测定出来。 J积分就是这样的一个理想的场参量。 已经证明, 对于单一材料裂纹扩展, 在线弹性状态下, 断裂力学中的J积分等于能量释放率G;或者当应力很低, 且裂尖塑性区尺寸相对于裂纹长度和试样尺寸很小时, 也可认为J积分等于能量释放率G。 所以可以以J积分幅值作为控制参量, 可得Paris方程的修正形式:
| $\frac{da}{dN}={{C}_{J}}{{\left( \Delta J \right)}_{{}}}^{mJ}$ | (25) |
式中CJ、mJ为以J积分为控制参量时的材料常数。
2.3 基于损伤力学的沥青路面破坏力学模型 2.3.1 疲劳损伤在交通荷载作用下, 路面实际受到一个反复动态加载—卸载的过程, 所以疲劳损伤的描述显得尤为重要。 在交变荷载作用下, 结构中会有大量的微裂纹形成, 并且微裂纹随着荷载循环次数的增加而逐渐扩展, 最终形成宏观裂纹, 导致材料的断裂, 这种破坏称为疲劳损伤破坏。 在结构破坏之前的荷载循环次数NF称为疲劳寿命。 对于应力水平较低的高周疲劳, 变形主要为弹性疲劳。 对于应力水平较高的低周疲劳, 则往往有塑性变形发生。 疲劳过程中的损伤问题由于其重要的工程意义而得到了人们的高度重视。
在疲劳损伤理论中, 损伤常常表示为荷载循环次数的函数。 一般情况下, 疲劳损伤的演化方程可表示为如下形式:
| $\delta D\text{ }=\text{ }f\left( D, \text{ }\Delta \sigma , \bar{\sigma }\text{ }, \text{ }\ldots \right)\delta N, $ | (26) |
式中:D为损伤变量;Δσ为荷载循环中的应力变化幅度, 简称应力幅;为平均应力。
随着荷载循环次数的增加, 损伤逐渐积累。 如何处理损伤的累积, 是疲劳分析尤其是像交通荷载这种多级加载情况下疲劳分析中的一个重要问题。 在多级加载情况下, 一个最简单的、被广泛采用的疲劳寿命估计方法是Miner线性累积法。 设材料依次承受应力幅为Δσ1、Δσ2、…的循环荷载作用, 经历的荷载循环次数分别为ΔN1、ΔN2、…, 假设其间损伤的发展ΔD1、ΔD2、…分别与ΔN1/NF1、ΔN2/NF2、…相联系, 其中NF1、NF2、…为Δ σ1、Δσ2、…分别单独作用时的疲劳寿命。 根据Miner的损伤线性累积律, 疲劳破坏准则可以表示为
| $\sum \frac{\Delta {{N}_{i}}}{{{N}_{Fi}}}=1。$ | (27) |
因此, 在等应力幅的循环载荷作用下, 可以认为损伤的演化是线性的, 即
| $D=\frac{N}{{{N}_{F}}}, $ | (28) |
这是一种最简单的疲劳损伤定义。 后来, 有学者通过试验提出了合适的损伤变量随循环作用次数变化的损伤演化方程, 如CHABOCHE J L提出了一种针对单向拉伸的损伤演化方程[25]如下:
| $\frac{dD}{dN}={{[1-{{\left( 1-D \right)}^{1+\beta }}]}^{\alpha }}{{\left[ \frac{\Delta \sigma }{M\left( 1-D \right)} \right]}^{\beta }}, $ | (29) |
式中:α、β、M是与温度有关的材料参数, α还与应力幅有关, α=α(σ), M还与平均应力有关, M=M(σ)。
2.3.2 蠕变损伤在我国, 车辆超载严重, 大车车速慢, 所以路面破坏中蠕变损伤效应非常显著。 蠕变损伤的机理和特征与疲劳完全不同, 其性质完全取决于时间, 即具有时间依存性。 20世纪50年代, Kachnov蠕变损伤模型被提出, 即用有效面积的缩减来定义蠕变损伤。 在微观机理上, 衰变的部分面积可以解释为由于晶界面上出现空洞或其它微观缺陷所造成的无效面积, 各种宏观连续损伤理论的发展也源于这一定义基础。 Kachnov蠕变损伤模型是最为基础、应用最广泛的一种, 其演化方程如下
| $\frac{dD}{dN}=A{{\left( \frac{\sigma }{1-D} \right)}^{n}}, $ | (30) |
式中, A、n为材料的常数。
随着对蠕变损伤研究的逐步深入, 人们考虑到初始应力水平对蠕变损伤的影响, 对上面的蠕变损伤模型进行了改进, 并在此基础上提出了经典的韧性蠕变断裂损伤方程。
2.3.3 疲劳-蠕变损伤由于交通荷载的特殊性, 路面破坏实际上是疲劳和蠕变两种损伤耦合在一起的。 特别是在一些大车慢行和停靠路段, 如长大纵坡、城市公交车站和路口等路段。 蠕变和疲劳分别属于两种不同类型的损伤过程, 两者不仅成因不同, 且分布“形态”也不尽相同, 即会产生不同形式的微观缺陷, 疲劳损伤Df表现为在较大范围内的较均匀分布, 而蠕变损伤Dc则表现为在某一局部的高密度分布。 因此在疲劳-蠕变共同作用下, 沥青混合料损伤和破坏形式既不同于单纯蠕变又不同于疲劳加载。 疲劳和蠕变是两个相互影响的过程, 在高温下每一个加载循环中既产生一定程度的疲劳损伤, 也产生一定程度的蠕变损伤。 无论哪种损伤积累到临界状态时, 都导致断裂。 在蠕变疲劳交互作用过程中, 两者相互影响和相互制约。
关于疲劳-蠕变交互耦合作用, 在金属材料领域疲劳—蠕变交互作用模型的应用十分广泛, 研究也相当成熟, 然而在沥青混合料这方面, 有待深入系统的研究。 目前主要有寿命-时间分数法、应变范围划分法、应变能划分法及应变松弛范围法等几种疲劳-蠕变损伤确定方法[26]。 下面仅介绍寿命-时间分数法。
寿命时间分数法简单, 易于应用, 认为疲劳蠕变交互作用的损伤为疲劳损伤和蠕变损伤的线性累积, 即
| $\sum\limits_{i=1}^{n}{\frac{\Delta {{N}_{i}}}{{{N}_{fi}}}}+\sum\limits_{i=1}^{n}{\frac{\Delta {{t}_{i}}}{{{t}_{Ri}}}}=D, $ | (31) |
式中, Nfi为疲劳寿命, ΔNi为疲劳循环次数, tRi为蠕变破坏时间, Δti为蠕变保持时间。
LAGNEBORG R和ATTERMO R及陈国良和谢锡善等在式(31) 理论基础上, 又分别提出了相应的非线性叠加模型[27-28]
| ${{D}_{c}}+D+A{{(D{{D}_{c}})}^{1/2}}=1, $ | (32) |
| ${{D}_{c}}+D+B{{D}^{n}}_{c}{{D}_{f}}^{1-n}=1, $ | (33) |
以上两式中, Dc为蠕变损伤;Df为疲劳损伤;A和B为疲劳—蠕变交互系数, 当A>0或B>0, 表明两者为正交互, 当A<0或B<0时为负交互。
这两个模型所需试验方法简单, 只需要获得相应环境温度下的纯蠕变和纯疲劳数据即可。
3 沥青路面车辙力学机理与预测模型在行车荷载反复作用下, 沥青路面结构层会产生竖向永久变形的累积, 该永久变形与土基、基层的变形以及沥青混合料的黏滞流动都有一定的关系, 并包括材料磨耗和压实效应。 根据车辙成因不同, 路面车辙大致分为4类:结构性车辙、失稳性车辙、磨损性车辙和压密性车辙。
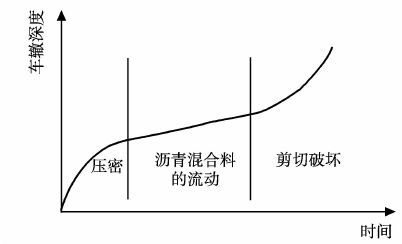
3.1 车辙形成机理[29-30]一般将车辙的演化过程分为如图 4所示的3个阶段。
|
图 4 沥青路面车辙形成过程示意图 Figure 4 Schematic of the rutting formation of asphalt pavement |
第一阶段:开始阶段的压密过程。 在被碾压成型前, 沥青混合料是由沥青、粗细骨料和空气组成的松散混合物。 高温碾压过程中, 由沥青、矿粉组成的胶浆以及半流体状的沥青被挤进矿料间隙, 与此同时粗细骨料也被碾压而排列形成一定骨架的结构。 在施工完毕的初始运营状态, 汽车轮载将继续这一压密作用, 因而此密实过程还将继续发展。
第二阶段:沥青混合料的流动过程。 在高温下, 沥青混合料呈现出以黏性为主的半固体状态。 过大的荷载作用将使沥青、沥青胶浆产生黏性流动, 从而使沥青混合料密实的骨架结构失稳。 沥青、沥青胶浆在荷载作用下除部分填充混合料空隙外, 还将随沥青混合料而自由流动, 从而使得荷载作用处的沥青混合料变形严重。
第三阶段:矿质骨料的重新排列及矿质骨料的破坏过程。 由于沥青、沥青胶浆在荷载作用下已发生流动, 半固态沥青混合料中粗、细骨料组成的骨架结构已逐渐承担了大部分的荷载, 在荷载和沥青润滑的双重作用下, 矿料颗粒沿矿料间接触面滑动, 从而使沥青、沥青胶浆向其富集区流动, 最终流向沥青混合料的自由面。
3.2 沥青路面车辙预测方法[31-33]建立科学合理的车辙预估模型, 对防止和减少车辙的危害, 提高路面的使用寿命, 选择合适的维修养护时机, 提高路面的管理水平, 都具有重要意义。 下面将简要论述国内外发展的主要车辙预测方法。
(1) 理论方法
1974年由HILLS J F等提出的SHELL车辙计算方法是目前力学法中应用最广泛的方法之一, 其实际上是基于弹性层状体现理论发展起来的[34]。 其假定沥青混合料的变形是相邻矿料间的滑移造成的, 并从蠕变试验中得到沥青混合料的劲度与沥青劲度之间的关系。 计算公式为
| $RD={{C}_{m}}{{Z}_{0}}\sum\limits_{i=1}^{n}{\left( \frac{{{\sigma }_{av}}}{{{S}_{mix.\eta }}} \right)}{{h}_{i}}, $ | (34) |
式中, RD为车辙深度;Cm为动态修正系数;Z0为构造因子;σav为第i层平均压应力;Smix.η为第i层黏滞劲度;hi为第i层厚度。
该方法优点是考虑了动态效应, 但仅对弹性响应精确;将劲度参数作为弹性参数, 未考虑混合料的黏性和塑性效应。
HUSCHEK S于1979年提出了修正的Maxwell模型以表征混合料的黏弹特性, 采用黏弹性层状体系首先计算路面层的应力应变分布[35];然后根据车速, 将静态应力、应变转变为时间的函数, 并假定应力应变为线性关系。 计算公式如下:
| $RD=\int{\int_{0}^{h}{\varepsilon }}\left( z, \text{ }t \right)dzdt=\int{\int_{0}^{h}{\sigma }}\left( z, \text{ }t \right)/\eta \left( t \right)dzdt, $ | (35) |
式中, ε(z, t)为面层z深度处的永久应变;σ(z, t)为z深度处的竖向压应力;η(t)为黏度系数;t为时间。
该方法是基于黏弹性层状体系提出的, 考虑了时间硬化作用, 可以反映侧向流动, 但黏弹性应力是由车速转换而来。
1995年张登良等采用弹性层状体系理论和流变学模型, 考虑路面结构为多层轮载动态效应和侧向隆起, 得到高等级沥青混凝土路面车辙预估模型[30]
| $RD=\left[ \sum\limits_{i=1}^{n}{{{C}_{di}}}(\frac{{{E}_{i}}}{{{S}_{mix, \text{ }p}}}\times {{\delta }_{i}}) \right](1+{{K}_{L}}), $ | (36) |
式中, Ei为第i亚层沥青混合料的弹性模量;Smix, p为第i亚层沥青混合料的黏性劲度模量;KL=0.5, 为侧向隆起系数;Cdi为第i亚层沥青混合料的动态修正系数;δi为第i亚层沥青混合料上层面与下层面的垂直变形之差。
该模型与SHELL的模型类似, 采用弹性层状体系理论进行路面内的应力计算, 采用蠕变试验确定沥青材料的劲度模量。 虽然考虑了动载荷材料的侧向隆起流动, 但参数的确定有很大的经验性。
SOUSA J B等于1994年提出了沥青混合料黏弹塑性模型, 并基于该模型得到了车辙深度与最大永久应变的关系[36]:
| $RD=\mu {{\gamma }_{max}}, $ | (37) |
式中, γmax为最大永久剪应变;μ为系数。 式(37) 虽然考虑了剪应力和非线性, 但广义Maxwell模型不能很好地模拟有些混合料的黏弹性行为。
徐世法和朱照宏基于 “四单元五参数”黏弹性模型, 提出了车辙预测公式[37]:
| $RD=\sum\limits_{i=1}^{n}{({{W}_{t1, \text{ }i}}-{{W}_{t2, \text{ }i}})}, $ | (38) |
式中, Wt1, i为第i级荷载加载时的总变形;Wt2, i为第i级荷载卸载后的回弹变形。
“四单元五参数”模型虽然能近似地表示沥青混合料的黏弹特性, 但是元件越多, 设计时所需要的参数就越多, 而材料参数的确定是一件相当复杂的工作。
(2) 经验方法
经验法也可以看成是一种统计方法, 出现时间较早。 SHAMI H I于1997年提出了基于APA试验的车辙预估模型[38]:
| $\left[ \frac{RD}{R{{D}_{0}}} \right]={{\left[ \frac{T}{{{T}_{0}}} \right]}^{\alpha }}{{\left[ \frac{N}{{{N}_{0}}} \right]}^{\beta }}, $ | (39) |
式中, T为温度;N为加载次数;下标0表示参考值。
基于AASHTO试验路的数据, ARCHILLA A R和MADANT S[39]于2000年提出了如下预测模型:
| $R{{D}_{it}}={{\delta }_{i}}+{{a}_{i}}[1-exp\text{ }({{b}_{i}}{{N}_{it}})], $ | (40) |
式中, Rit为时间t和断面i的车辙深度;δi为断面i竣工时源于下卧层的车辙深度;Nit为时间t累积轴载次数;ai和bi为路面特性参数。
近年来, Bailey-Norton蠕变规律被广泛用于计算路面变形, 表达式为:
| $\varepsilon \prime =A{{\sigma }^{n}}{{t}^{m}}, $ | (41) |
式中, ε′为蠕变应变率;σ为单轴等效应力分量;t为总时间;A、m、n为材料参数。 该模型需要先通过室内试验获得材料参数, 然后通过分层叠加得到路面的车辙深度。
(3) 力学-经验方法
力学-经验法采用弹性或黏弹性层状体系理论计算应力和应变, 并结合试验, 统计得出车辙与材料特性、路面结构及荷载条件之间的关系。 1991年SHRP计划提出累积塑性应变同荷载重复次数的对数线性关系, 并进一步提出了一定轴载下路面车辙深度的计算方法。 但该方法认为车辙主要是压密产生的, 与中国实际情况不符, 且对温度考虑过于简单。
KENIS W J提出了基于力学计算和单轴重复加载试验的沥青路面车辙预估方法[40]:
| $\varepsilon {{\prime }_{p}}\left( N \right)=\varepsilon \mu {{N}^{-a}}, $ | (42) |
| $\begin{array}{*{35}{l}} {{\varepsilon }_{p}}\left( N \right)={{\int }_{0}}^{N}\varepsilon {{\prime }_{p}}\left( N \right)dN={{\int }_{0}}^{N}\varepsilon \mu {{N}^{-a}}dN= \\ \varepsilon \left( \frac{\mu }{1-\alpha } \right){{N}^{(1-\alpha )}}, \text{ } \\ \end{array}$ | (43) |
| $RD=\sum\limits_{i=1}^{n}{{{\varepsilon }_{pi}}{{h}_{i}}}, $ | (44) |
式中, ε为力学计算得到的应变;N为荷载作用次数;RD为永久变形量;εp(N)为累计应变;ε′p(N)为εp(N)随N的增长速率;hi为第i层厚度;μ为系数。
JACOB U提出了基于弹性或黏弹性层状体系的应力解, 再结合室内外的有关试验, 统计出沥青层的永久变形同路表弯沉、材料特性参数及荷载之间的经验关系[41]。 理论统计法提出的预估模型, 经过与试验数据的经验拟合回归, 提出如下公式:
| ${{\varepsilon }_{p}}=\frac{{{\alpha }_{1}}}{W(1+{{\alpha }_{2}})}\delta {{N}_{2}}^{(1+\alpha )}, $ | (45) |
式中, εp为永久性变形;W为弯沉系数;δ为双轮动态荷载下的弯沉;α1、α2为系数。
此方法虽考虑了路面结构的整体效应, 但力学理论不够完善, 对路面各结构层尤其是面层的变形情况考虑得太少, 无法预估不同时期的车辙深度且参数难以确定。
2000年, MONISMITH C L提出了一种应变的替换方法, 以此表征路面车辙[42]。 假定路面为多层弹性体系, 基于非线性的弹性理论求解, 混合料模量由重复荷载简单剪切试验获得。 计算轮迹边缘下50mm处的永久剪应变的累积值, 计算公式为:
| ${{\gamma }^{i}}=a\text{ }exp\left( b\tau \right){{\gamma }^{e}}{{N}^{c}}, $ | (46) |
式中, γi为50mm深度处永久剪应变;τ为同深度处剪应力;γe为弹性剪应变;N为荷载重复次数;a, b, c为常数。
FWA T F等2004年基于沥青混合料的剪切流动变形原理, 采用c-φ模型进行预估, 模型如下[43]:
| $RD=C\sum\limits_{i=1}^{n}{[{{({{N}_{i}})}^{a}}{{({{L}_{i}})}^{b}}{{({{T}_{i}})}^{c}}{{({{t}_{i}})}^{d}}]}, $ | (47) |
式中, C为轮迹分布影响系数;Li为实际受力与路面能承受的最大抗力的比值;Ti为路面温度;ti为轮载作用时间;Ni为轮载作用次数。
该模型基于沥青路面车辙的发生机理, 综合考虑了影响车辙的各种因素, 是力学-经验法的典型代表。 但是该预估模型中Li的意义并不明确(剪应力或拉应力), 且模型的建立仅限于室内试验, 还需要现场数据的进一步修正。
曹卫东等基于修正Burgers蠕变模型开展了两类沥青路面的车辙数值模拟, 建立了相应的车辙发展深度(RD)与轴载作用次数(T)之间的模型方程计算[44-46]。
| $\text{lg}RD=a{{T}^{b}}, $ | (48) |
式中, a、b为回归系数, 采用该预估模型可以预测两类沥青路面车辙破坏发生的时机。 当然, 该经验模型具有一定的局限性, 需要依据不同的沥青材料类型、现场路面车辙数据进行修正。
4 沥青路面水损坏力学机理与水的作用有关的早期破坏现象统称为水损坏, 如沥青面层麻面、松散、掉粒、析油、唧浆、坑洞、网裂等破坏现象。 水损坏机理非常复杂, 涉及到水与沥青混合料的物理化学作用及流固耦合力学。 沥青路面发生水损坏离不开水的参与, 通常沥青路面中水分来源主要有三个途径:地表降水导致水流通过路面孔隙自上而下渗入路面内部;地下水自下而上进入路面结构内部;湿集料微观孔隙内原本存在水[47]。
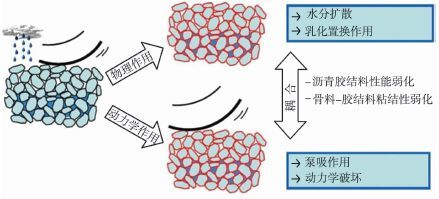
4.1 水损坏的微观力学机理水进入路面结构之后会对路面产生两种作用:一种是无车载等外力作用时(即静水状态)发生水分在沥青膜内的扩散, 并对沥青膜产生乳化置换作用;另一种是在移动车载等外力条件下发生泵吸作用和动力学破坏, 见图 5 [47]。
|
图 5 沥青路面水损坏的物理-力学作用 Figure 5 Physical-mechanical effect on moisture damage in asphalt pavement |
在静水作用下水与沥青膜、集料发生一系列物理化学反应, 导致沥青膜剥落, 发生路面黏结破坏。黏结破坏与下列一种或两种现象有关:一是水与黏结剂相互作用导致黏结强度和混合料刚度降低;二是水能够进入沥青膜和集料之间的缝隙中, 破坏黏结力, 最终将沥青黏结剂从集料上剥离。沥青膜内包裹沥青分子高极性基团或水溶性杂质(如离子、盐)的地方为亲水区[48], 当沥青-集料交界面中短时间内存在大量水或在交界面内存在薄水层时, 水分由于亲水性或沥青膜内部分杂质的水溶性开始移动。另外, 在沥青膜内水溶性杂质和高极性基团是相互联系的, 二者一般同时存在[49-50]。水溶性物质在沥青-集料交界面形成了水溶层, 导致水膜形成, 最终使得沥青剥落、集料交界面黏附性丧失[51]。此外, 沥青-集料的黏结力还受到很多因素影响, 如界面张力、集料温度、沥青黏结剂化学成分、 拌合中界面含水量等。黏结性是沥青-集料界面的基本性质[52], 沥青和集料之间的分子力在黏结体系中起着重要作用, 润湿和联锁的物理化学性能对分子力有很强烈的影响。因此, 路面材料的黏结强度与沥青-集料间的相互作用、亲和力和吸引力有密切关系。可以说沥青和集料的化学性质主要影响了黏结性[53]。
四种常见的黏结性理论是表面能理论、力学联锁理论、化学反应理论和分子定向理论。表面能理论发展很快, CHENG D的研究成果表明, 表面能能够较好地表征沥青对集料的黏附性, 根据它来预测沥青的剥落是可行的[54]。ARABANI M和HAMEDI GH H根据表面自由能机理, 采用Wilhelmy平板和通用吸附设备(WP和USD)法评估了半晶质聚乙烯(PE)作为集料包裹物时, 不同密度的PE材料对水损坏的影响, 他们发现PE材料的使用降低了水-集料的SFE, 使花岗岩和石英集料表现出更好的抗水损性能[55]。为了从根本上解释水损坏问题, WASIUDDIN N M等研究了温拌添加剂对表面自由能的影响, 他们发现根据SFE能够计算出沥青黏结剂在集料上的覆盖率, 并与沥青-集料的黏结性联系起来, 另外, 聚苯乙烯-丁二烯-苯乙烯(SBS)改性剂能将亲水性黏结剂变成疏水性黏结剂, 从而增强沥青混合料的抗水性[56]。
沥青黏结剂的分子结构和化学成分以及不同类型集料的化学性质对路面黏结破坏有着重要影响。沥青分子体系复杂, 会发生很多相互作用, 在不同温度下沥青分子的运动受到这些相互作用的控制[57]。研究发现, 沥青和集料在相互作用时会产生共价键[58]。根据分子定向理论, 沥青分子在集料附近时, 由于极性沥青分子会沿集料表面方向自动排列[59], 但当水进入到集料表面后, 将发生一系列水化过程并开始缓慢分解, 从而改变邻近水层的pH值[60], pH的变化会改变电离状态以及集料吸附的极性基团类型, 导致集料沥青表面相反的、带负电荷的双电层增强, 并最终使沥青和集料分离[60-61]。
另外一些学者, 如RICE J M和THELEN E提出集料表面纹理是影响沥青集料黏结性能的主要因素, 他们主要考虑力学咬合作用而忽视沥青和集料间的化学作用, 并假设黏结剂的内聚力和集料颗粒的咬合性能(包括个体的晶面、吸水性、表面包裹、棱角及集料孔隙率等)对黏结强度都有影响[62-63]。如果这些性能不足以产生明显的咬合体系, 则在水的作用下沥青和集料间就很可能发生黏结破坏[64]。另外, 研究发现, 表面有较多孔隙并且纹理粗糙的集料抗水损坏的能力越强[65], 有较多棱角的集料会有更好的力学联锁效应[66]。
4.2 水损坏的流固耦合动力学分析美国沥青协会曾对沥青剥落过程进行过较深入研究, TERREL R L和AL-SWAILMI S把沥青膜的剥落机理归纳为撕裂、置换、瞬间乳化、孔隙水压力、水力冲刷等几种情况, 具体来说, 有以下几种模式:(1) 沥青膜移动;(2) 沥青膜分离;(3) 沥青膜破裂;(4) 起泡;(5) 水力冲刷和孔隙压力;(6) 黏结层破坏[67]。水的作用不仅表现在静水与沥青膜之间的物理化学作用, 而且水力(包括动孔隙水压力与冲刷力)在水损坏过程中同样起了重要的驱动作用。行车荷载作用在沥青路面上, 路面孔隙中将先后产生正动水压力和真空负压的泵吸作用, 这一过程中水的反复冲刷会加速产生水损坏, 因此需要对水损坏进行流固耦合动力学理论分析。
影响动水压力的因素很多, 主要有以下4个方面的因素[68]。
(1) 车速
降雨条件下车轮挤压路表水膜产生的瞬时水压力, 称之为动水压力, 它是引起路面动力水损坏的重要原因。实际上这一水压力仅为外水压力, 与车载作用下路面介质体积变形引起的内动水压力相比, 其直接作用不大, 在对动水压力进行数值模拟过程时将作为边界条件施加。为了与路面内动水压力相区别, 称之为路表动水压力。路表动水压力的存在会产生两种效应:一是减小车轮对路面的法向作用, 进一步减小摩擦力;二是会对路面结构内部水压产生影响, 因为路表水和内部水是相通的。路表动水压力随车速增加而不断增大, 如图 6所示[69]。另一方面, 车载作用下路面变形响应与车速有关, 这进一步影响路面内的动水压力, 车速越大, 车载作用时间越短, 水压的产生速度越大于消散速度, 使得动水压力越大。

|
图 6 路表动水压力与车速的关系曲线 Figure 6 Relation curve of surface hydrodynamic pressure and vehicle speed |
(2) 车载
目前我国重轴载车辆不仅数量多, 而且超载严重。车辆荷载越大, 路面弯沉值越大, 路面材料的体积变形越大, 路面内的孔隙水受挤压越强烈, 产生的动水压力越大。
(3) 路面材料
路面材料对动水压力的影响主要反映在不同材料具有不同的刚度、孔隙率、渗透系数及连通程度等。材料刚度越大, 体积变形越小, 动水压力越小;一般情况下孔隙率越大、孔隙联通程度越好, 沥青混合料渗透系数越大。大量实践表明, 沥青混和料孔隙率为8%~10%时, 沥青路面水损坏最为严重, 此时水一方面容易进入面层内部, 另一方面又不易排出, 长时间滞留在面层内, 在动车载作用下容易诱发很高的动水压力, 从而加剧水损坏的发生。
(4) 路面结构
路面结构对动水压力的影响很大, 为了达到不同的设计目的, 研究者设计了多种路面结构。柔性和半刚性沥青路面因为整体刚度不同, 内部产生的动水压也不同;OGFC排水路面、排水基层路面及“上封下排”路面因为排水隔水方式不同导致动水压力也不同。
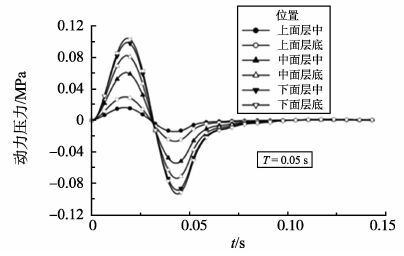
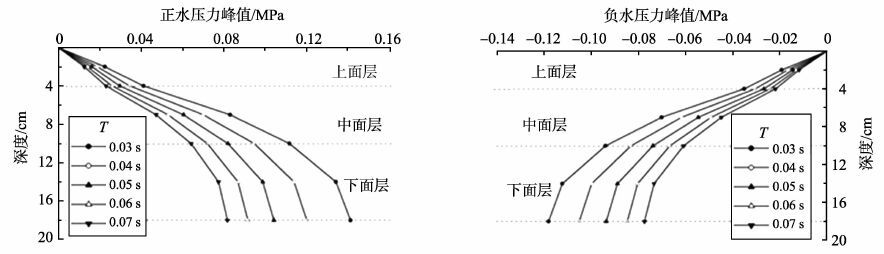
CUI X Z等通过渗透系数试验、汉堡试验等研究了HMA(Hot Mix Asphalt)路面车载引起的力学破坏对水损坏的影响, 发现车载引起的力学破坏在路面水损坏过程中有重要作用, 尤其是高温高湿环境下[70]。基于超声波法, 崔新壮等提出了路面损伤表征方法, 并建立了损伤与渗透性的关系[71]。为了研究饱水沥青路面在车载作用下的动态响应, 崔新壮等研究者还基于Biot固结理论, 用快速Lagrange有限差分法对路面进行了动态流固耦合分析, 得到了重要结论。车载作用过程中正负水压力交替出现(见图 7), 反复泵吸过程是路面水损坏产生的主要力学机理;动水压力随车速增大而增大(见图 8), 且最大值出现在面层底部, 因此面层底部若设有排水层则会有效防止水损坏发生[72-74]。其他一些学者做了类似研究, GAO J Q采用光线液压传感器对不同车速下孔隙水压力进行测量, 发现随着车速的增加, 孔隙水压力不断增大, 但压力持续时间呈下降态势[75]。薛强和盛谦研究了沥青路面破坏的多场耦合效应, 并提出了路面结构体破坏的秸秆纤维化控制技术[76]。吴国雄等采用ABAQUS软件建立了降雨入渗条件下沥青路面的有限模型, 来研究路面结构的渗流规律和渗流场的分布状态, 并基于多孔介质流固耦合理论, 分析了行车荷载作用下路面结构的力学响应[77]。结果发现, 潮湿状态沥青路面在车载作用下, 内部先后产生正负压的泵吸作用与反复冲刷过程, 孔隙水压与水流速最大位置分别位于沥青面层的底层与上层, 另外, 在水与荷载的动态耦合作用下, 结构层层底主应力与剪应力均呈现波动特性。邓融应用ANSYS有限元软件对动荷载作用下饱水沥青路面进行了数值模拟, 分析了饱水沥青路面内部的孔隙水压力、竖向位移、竖向应力、水平应力的时程变化情况[78]。计算结果表明, 在动荷载作用下沥青路面内部产生正、负逆转的孔隙水压力, 这种孔隙水压力的反复作用将加速水损坏的出现。
|
图 7 轮隙中心正下方动水压力的长消历程曲线 Figure 7 Hydrodynamic pressure dissipation history curve under wheel gap |
|
图 8 不同车速下动水压力竖向衰减曲线 Figure 8 Hydrodynamic pressure vertical attenuation curve of different speeds |
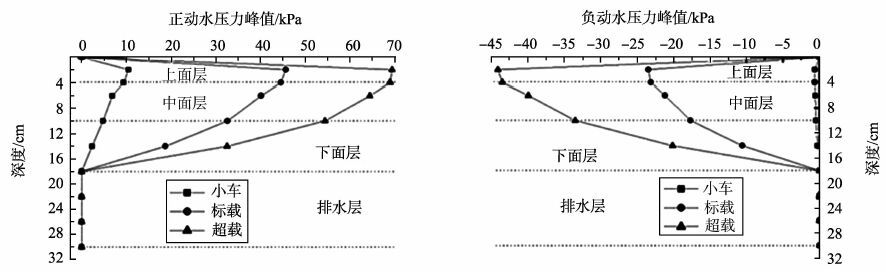
欧金秋在其他工况相同情况下, 通过改变车载大小研究了车载对动水压力的影响(见图 9)[79], 发现动水压力随车载增大而明显增大, 当超载50%时, 正动水压力峰值增大1/3多, 负动水压力峰值增大约1/2, 可见大车尤其是超载大车是造成路面水损坏的主要车型, 小车的影响可以忽略。
|
图 9 不同车载作用下动水压力竖向衰减曲线 Figure 9 Hydrodynamic pressure vertical attenuation curve of different vehicle loads |
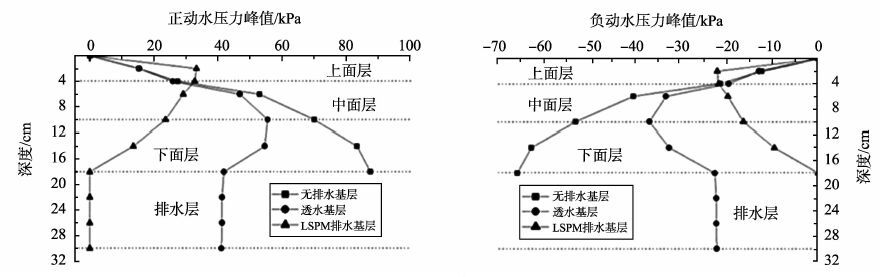
CUI X Z在沥青路面水损坏的研究中对比了两种不同路面结构动水压力的变化(图 10), 即设置排水层和无排水层两种路面结构[80]。发现不设透水层或排水层时, 动水压力随深度一直增大;对设透水层路面, 动水压力峰值随深度先增大后减小, 在排水层内基本稳定。透水效果越好, 对动水压的抑制作用越强, 说明增设排水层不仅能够将水快速排出, 而且能有效减少动水压力、抑制水损坏的发生。
|
图 10 不同路面结构动水压力竖向衰减曲线 Figure 10 Hydrodynamic pressure vertical attenuation curve of different structural layers |
沥青路面抗滑性能与路面表层的纹理构造直接相关[81], 路面纹理主要由沥青路面骨料颗粒的形状、大小、分布与骨料材质决定。将路面的形貌按平面尺寸和高度尺寸分为四种纹理[82-83]:微观纹理、宏观纹理、粗大纹理和不平度。微观纹理一般指波长1μm~0.5mm、高度方向1μm~0.5mm的纹理, 主要指骨料表面的微观形貌, 由骨料的材质和加工方式决定。宏观纹理一般指波长0.5~50mm, 高度方向0.5~20mm的纹理, 主要由骨料的形状、大小、分布决定。微观纹理是影响各种车速情况下路面抗滑性能的主要因素, 其基本决定了路面的抗滑水平;宏观纹理影响路面抗滑性能随速度衰减的幅度和雨天路面抗滑性能。随着道路运营时间的延迟, 路面纹理会发生磨损, 最终导致道路路面抗滑性能的降低。所以, 研究路面磨损机理具有重要工程意义。
5.1 磨损机理集料种类不同, 磨损机理也就不同, 如沉积岩磨损以层状(如石灰岩)和粒状(如砂岩)脱落为主, 岩浆岩(如玄武岩等)则呈现粒状、块状脱落、局部不均匀磨蚀和裂缝的综合磨损状态。集料矿物硬度越大, 则磨损量越小, 如沉积岩中的石灰岩主要成分是方解石, 其莫氏硬度只有3, 而岩浆岩以长石成分居多, 对应莫氏硬度可达7左右, 因此石灰岩的磨损量较玄武岩等要大。磨损对于路面宏观、微观构造的影响机理不同, 因此对路面的抗滑能力也有不同的影响效果, 主要体现在:一方面是对路面宏观构造的影响, 新建路面在车轮作用下, 裸露集料棱角“尖峰”被逐渐磨损, 宏观构造减小, 路面与车轮的啮合能力降低是导致路面抗滑能力减小的主要原因;另一方面是对微观构造的影响, 即在车轮对裸露集料的磨耗过程中, 都会造成集料表面微观构造的结构性再生, 路面微观构造基本上处于一个比较稳定的状态, 而微观构造与摩擦系数有很好的对应关系, 故摩擦系数受磨损的影响变化不大。
根据微细观机理的不同, 路面构造磨损一般可分为黏着磨损、磨粒磨损、疲劳磨损、侵蚀磨损四种形式。黏着磨损理论是由HOLM R及BURWELL J T和STRANG C D提出的, 认为两个相互作用的表面仅在少数几个孤立的凸出点发生接触, 导致这些接触面产生很高的应力, 这些微凸体发生黏着, 相对运动时, 内聚力较弱的一方的微凸体即被对方材料俘获[84-85]。这一理论指出, 材料的磨损与作用面的垂直荷载和滑动距离成正比, 而与材料的屈服应力成反比。20世纪70年代以来, 随着断裂力学的迅猛发展, 材料的磨损理论得到不断充实和完善, 路面的磨损过程被解释为一个“断裂过程”, 即表面材料经受着裂纹形成、稳定扩展、失稳扩展及碎屑脱离本体这一循环过程。SUH N P根据断裂力学理论提出的脱层磨损理论认为磨损是空穴生核率、裂缝扩展率、摩擦系数及硬度的函数[86]。磨粒磨损是指外界硬颗粒(碎石子和砂砾)在轮胎碾压和冲击作用下对路面构造造成的磨损。如果冲击角很大, 则将产生切削破坏;如果冲击角较小, 则将产生犁沟破坏, 最终碎屑在高速车轮带动下剥落。而疲劳磨损是当路面受到车辆移动的推压力作用时产生的, 最大法向正应力虽然就在表面上, 但最大剪应力却发生在表面以下的次表面层, 在受力点前后分别形成压力区和拉力区。由于接触应力的移动和反复作用, 路面不断承受着周期性扰动, 一些原生裂纹源则成为疲劳裂缝引发源, 可导致表面裂缝的扩展, 最终引起路面表层的局部断裂, 微观构造和宏观构造都可能因此而减小。侵蚀磨损则是当路面上存在可产生化学反应的物质时, 经过接触、滑动摩擦造成的磨损。其实这四种磨损形式往往同时发生, 如疲劳磨损贯穿了磨损整个过程, 只是程度不同而已。
5.2 抗滑性能的衰减规律沥青路面抗滑性能受到许多方面因素的影响, WILSON D J和DUNN R C M等研究影响道路抗滑性能的因素, 发现构成道路摩擦学系统主要包括四大方面:路面、车辆、周围环境以及其他[87]。
由于车辆轮胎与沥青混凝土表面是黏弹性材料, 其性质受温度影响显著, 因此路面抗滑性能的季节性波动非常明显, 在冬季的抗滑性能最高, 春秋次之, 夏季最低[88]。这是因为随温度升高橡胶轮胎的弹性增大、滞后损失降低, 降低了抗滑性[89];而气温较低时, 寒冷的环境和日常维护工作会使道路微观纹理增加, 所以冬季路面的抗滑性更好一些[90]。从一些路面的显微照片也可以看出, 由于集料的自然风化, 冬季道路的表面微观粗糙度会达到最大值;而在夏季这些微观粗糙度会由于车辆严重的磨光作用而消失[91]。LUO Y J在研究了路面温度对抗滑性能的影响后发现, 低车速下, 温度越低, 滑动阻力越大, 但在高车速下趋势相反[92]。降雨也是短期影响抗滑性能的一个因素, 刘君和李长城等研究了水膜对抗滑性能的影响, 并对水膜厚度做出了规定, 研究发现, 降雨过后的短期内路面会比干燥期间更滑, 导致交通事故明显增多, 这是因为雨水会与路面上的污染物(如碎石、尘土、油污等)混合, 降低了摩擦力[93-94]。不过由于雨水冲走了路面上的污染物, 雨水的这种作用会在降雨结束后慢慢消失[95]。道路上污染物的来源很多, 包括路面周围环境、行驶在路面的汽车以及路上的行人等[96], 不同性质的污染物对路面抗滑性的作用不同。坚硬但较细的污染物会明显降低路面抗滑性能, 因为这些污染物会加速路面磨光;而颗粒较粗较硬的污染物会提高抗滑性能, 因为它们使得路面更加粗糙[97]。刘明智也得到同样结论, 另外还发现少量土砂能够加速路面抗滑性能衰减, 并且油污虽然会降低路面抗滑性能, 同时也阻碍了抗滑性能的衰减[96]。
在车辆和道路材料等因素对沥青路面的抗滑性能的影响方面, 国内外专家也做了研究。肖鑫等在不同荷载作用下研究了沥青路面抗滑性能的衰减规律, 采用摆值(Fb)和构造深度(TD)作为抗滑性能指标, 发现随荷载的增大, 沥青混合料性能衰减越快, 且衰减幅度也越大[98]。孙洪利采用自主研发的沥青路面抗滑模拟试验机, 提出了Asymptotic指数模型抗滑性能衰减曲线, 并发现集料的种类和级配对抗滑性能衰减有明显影响, 较大的矿料粒径有助于提高抗滑性能[99]。针对不同路面类型, 宫秀青跟踪监测了其抗滑性能衰减情况, 其中超薄磨耗层(UTWC)路面初期抗滑性最强而后期呈速度较快的指数型衰减, 沥青马蹄脂(SMA)路面抗滑性无明显衰减[100]。李波研究了路表纹理的分形特征与抗滑性能关系, 采用分维值表征路表纹理, 发现了分维值与摩阻系数间的线性关系[101]。HOGERVORST D对比了不同车速下路面构造深度以及集料表面微观纹理对于路面抗滑性能的影响, 发现低速下集料表面微观纹理显著影响轮胎的抗滑性能, 宏观构造深度则影响很小, 随着速度的增加, 集料的微观纹理对于轮胎的摩擦贡献减小, 宏观构造深度则通过降低摩擦速度的衰减速率以及在路面存在积水时增加排水量实现增加路面的抗滑性能[102]。另外, 法国学者还发现路面材料老化对抗滑性能有重要影响, 对轻交通道路, 路面材料老化能提高路面抗滑能力。
赵战利和杨众等为了对沥青路面防滑性能衰变机理进行分析, 研制开发了小型环道加速磨耗仪, 并利用该设备对防滑磨耗层防滑性能衰变规律、影响因素进行了初步研究[103-104]。孙洪利等研究发现新建沥青路面在行驶车辆的作用下, 路面混合料将随时间发生与抗滑性能相关的变化:压密变形、磨光和磨耗(磨损)[99]。这些变化往往同时发生, 区别在于衰减初期以压密变形为主, 衰减渐趋稳定以后则以磨光和磨耗(磨损)为主。沥青路面在建成初期混合料并不能达到最大密实或最稳定状态, 因受交通荷载的持续作用, 路面材料内部的矿料和胶浆将继续发生压密或迁移变形, 导致路表宏观构造深度降低, 影响路面的抗滑性能。磨光作用则是指行驶车轮对于路面, 尤其是路表裸露粗集料表面微观构造凸起的“削平”过程, 磨光效果与轮胎特征(硬度、花纹的构型和深度等)、集料特征(表面构造、棱角性、形状及矿物特征等)有关, 其中集料特征是路面磨光的决定性因素。新建路面在车轮的磨光作用下, 集料表面的沥青薄膜逐渐磨去, 车轮与路面之间的附着力会随着集料表面微观构造的外露而略有增加[105], 但这一过程一般持续时间很短, 有时甚至不太明显;随着轮载作用次数的进一步增加, 微观“凸起”构造在车轮压、剪作用下逐渐“削平”, 车轮—路面间附着力降低, 摩擦系数下降, 这一过程一直持续到微观构造的磨光和结构性再生之间接近某种平衡为止, 摩擦系数才相应稳定下来。磨耗(磨损)作用主要是指在车轮的磨耗过程中, 路面集料表面棱角被磨掉并发生明显变形的过程, 磨损效果除取决于车轮等因素外, 还与集料种类及硬度有关。
一般情况下, 集料的磨光和磨损(磨耗)过程同时发生, 并且都会导致路面抗滑能力的衰减, 但衰减机理不同:磨光作用主要是通过集料微观构造的降低来减小摩擦系数;而磨损(磨耗)作用主要通过对裸露集料棱角的磨耗使路表构造深度降低, 对于摩擦系数的改变则不明显。集料的磨光和磨损特性是集料矿物成分、晶体类型、斑晶数量及分布等各种因素共同作用的结果, 集料矿物成分的分布与摩擦系数有如下关系:矿物成分分布的均匀性越差, 矿物颗粒之间或矿物颗粒与基质之间的硬度相差越大, 就越有利于摩擦系数的提高。
6 结语(1) 沥青路面材料弹塑性模型有很多, 其中应变软化模型最能够反应实际情况, 软化会使材料内部形成剪切带, 出现剪胀现象。
(2) 相比现象学法和能量法, 损伤力学与断裂力学是路面破坏力学的主要框架, 在研究路面损伤和破坏规律中的应用更为普遍。基于断裂力学理论的Paris方程是研究循环荷载作用下路面开裂的基础, 后人在此基础上对Paris方程进行了一系列修正和改进;交变荷载和高温作用下, 沥青路面会同时出现疲劳和蠕变损伤过程, 二者相互影响制约。
(3) 沥青路面结构层在车载作用下经历压密、沥青混合料流动和剪切破坏的过程形成车辙。在车辙的预测方法中, 理论法在参数的确定方面有很大经验性且较为复杂;经验法是通过试验得到的材料参数计算车辙深度;力学—经验法经过修正完善, 考虑的因素较为全面, 但依然具有局限性, 需要进一步探究。
(4) 从微观角度, 沥青路面水损坏可以从物理化学作用和动力学角度解释, 流固耦合动力学分析在水损坏研究中有重要应用前景。经过数值模拟计算, 作者发现在沥青路面面层底部设置排水层能够有效降低移动车载作用下的动水压力, 减少水损坏发生。
(5) 沥青路面在外力作用下发生磨损, 引起抗滑性能的衰减, 这是路面、车辆、周围环境及其他因素共同作用的结果。
| [1] | GERBAULT M, POLIAKOV A N B, DAIGNIERES M. Prediction of faulting from the theories of elasticity and plasticity what are the limits?[J]. Journal of Structural Geology , 1998, 20 (273) : 301-320 |
| [2] | CHEN W F. Limit analysis and soil plasticity[M]. Amsterdam: the NetherlandsElsevier Publishing Company, 1975 . |
| [3] |
元松, 单景松. 基于FWD的柔性路面结构动力响应数值分析[J].
长沙交通学院学报 , 2006, 22 (2) : 33-37 YUAN Song, SHAN Jingsong. The numerical analysis of dynamic response of flexible pavement based on FWD[J]. Journal of Changsha Communications University , 2006, 22 (2) : 33-37 |
| [4] |
郑元勋, 杨培冰. 热一结构耦合作用下沥青路面动态弯沉温度修正研究[J].
郑州大学学报(工学版) , 2014, 35 (2) : 1-5 ZHENG Yuanxun, YANG Peibing. The study of dynamic denection temperature correction of asphalt pavement under effect of thermal-structure coupling field[J]. Journal of Zhengzhou University(Engineering Science) , 2014, 35 (2) : 1-5 |
| [5] |
黄磊, 冯铨, 杨阳, 等. 基于FWD 荷载作用的路面力学指标分析[J].
公路交通技术 , 2010 (2) : 214-222 HUANG Lei, FENG Quan, YANG Yang, et al. Analysis of mechanical indices of pavement under fwd load[J]. Technology of Highway and Transport , 2010 (2) : 214-222 |
| [6] |
赵杏梅. 动荷载作用下沥青路面动态响应研究[J].
湖南交通科技 , 2015, 41 (2) : 37-39 ZHAO Xingmei. The study of dynamic response of asphalt pavement under the effect of dynamic load[J]. Hunan Communication Science and Technology , 2015, 41 (2) : 37-39 |
| [7] |
刘宇星, 李玉华. 沥青路面塑性变形的有限元模拟分析[C]// 第八届全国土木工程研究生学术论坛. 杭州:浙江大学, 2011:1140-1145.
LIU Yuxing, LI Yuhua. Plastic deformation FEM simulation analysis of asphalt pavement[C]// Proceedings of the 8th National Civil Engineering Forum for Graduate Students. Hangzhou: Zhejiang University, 2011:1140-1145. |
| [8] |
郑健龙. 基于状态设计法的沥青路面弯沉设计标准[J].
中国公路学报 , 2012, 25 (4) : 1-9 ZHANG Jianlong. Deflection design standards of asphalt pavement based on state design method[J]. China Journal of Highway and Transport , 2012, 25 (4) : 1-9 |
| [9] | MONISMITH C L, SALAM Y M. Fracture characteristics of asphalt concrete[J]. Proceedings, Association of Asphalt Paving Technologists , 1971 : 215-256 |
| [10] | VAN DIJK W, MOREAUD H, QUEDEVILLE A, et al. The fatigue of bitumen and bituminous mixes[C]// 3rd International Conference on the Structure Design of Asphalt Pavement. London, UK: University of Michigan, 1972:254-366. |
| [11] | GROSS D, SEELIG T. Fracture mechanics with an introduction to micromechanics[M]. Berlin, Gemany: the Netherlands Springer Berlin Heidelberg, 2006 . |
| [12] | PARIS P C, ERDOGAN F. A critical analysis of crack propagation laws[J]. Transactions of the ASME, Journal of Basic Engineering, Series D , 1963, 85 (3) : 528-534 |
| [13] | MAJIDZADEH K, TALBERT L O.Development and field verification of a mechanistic structural design system in Ohio[C]// Volume I of Proceedings of 4th International Conference on Structural Design of Asphalt Pavements. Ann Arbor, Michigan, USA: University of Michigan, 1977, 22-26:402-408. |
| [14] | SCHAPERY R A. A theory of crack growth in visco-elastic media. Report MM 2764-73-1[R]. [S. l.]:Mechanics and Materials Research Center, Texas A&M University, 1973. |
| [15] | SCHAPERY R A. A theory of crack growth in visco-elastic media, Part Ⅰ: theoretical development, Part Ⅱ: approximate methods of analysis, Part Ⅲ: analysis of continuous growth[J]. International Journal of Fracture , 1975, 11 (1) : 141-159 DOI:10.1007/BF00034721 |
| [16] | SCHAPERY R A. A method for predicting crack growth in nonhomogeneous visco-elastic media[J]. International Journal of Fracture , 1978, 14 (3) : 293-309 |
| [17] |
谢涛. 基于CT实时观测的沥青混合料裂纹扩展行为研究[D]. 成都:西南交通大学, 2006.
XIE Tao. Study on crack propagation behavior of asphalt mixtures based on CT real-time observation[D]. Chengdu: Southwest Jiaotong University, 2006. |
| [18] | JACOBS MM J. Crack growth in asphaltic mixes[D]. Delft, Holland: Delft University of Technology, 1995. |
| [19] | ROSIER J, PETIT C H, AHMIEDI E, et al. Mixed mode fatigue crack propagation in pavements structures under traffic load. Reflective Cracking in Pavements[C]// International RILEM Conference on Reflective Cracking in Pavements, 3rd. Maastricht, the Netherlands:[s. n.], 1996: 143-152. |
| [20] | FORMAN R G. Numerical analysis of crack propagation in cyclic loaded structures[J]. Journal of Basic Engineering, Transaction ASTM (Series D) , 1967, 89 : 459-465 DOI:10.1115/1.3609637 |
| [21] | WALKER E K.The effect of stress ratio during crack propagation and fatigue for 2024 T3 and 7075 T6 aluminum[C]// Effects of Environment and Complex Load History on Fatigue, ASTM STP 462. [S. l.]:[s. n.], 1970: 1-14. |
| [22] | ELBER W. Fatigue crack closure under cyclic tension[J]. Engineering Fracture Mechanics , 1970 (2) : 37-45 |
| [23] | DONAHUE R J, MCI CLARK H, ATANMO P, et al. Crack opening displacement and the rate of fatigue crack growth[J]. International Journal of Fracture Mechanics , 1972, 8 (2) : 209-219 DOI:10.1007/BF00703882 |
| [24] | MCEVILY A J, GROEGER J. On the threshold for fatigue-crack growth[C]// Forth International Conference on Fracture. vol. 2. Waterloo, Canada: University of Waterloo Press, 1977:1293-1298. |
| [25] | CHABOCHE J L. Viscoplastic constitutive equations for the description of cyclic and anisotropic behaviour of metals[J]. Bulletin de lAcademie Polonaise des Sciences, S′erie Sc. et Techn , 1977, 15 (1) : 33-41 |
| [26] |
蒋丽君. 重复荷载作用下沥青混合料疲劳损伤与蠕变损伤特性研究[D]. 长沙: 长沙理工大学, 2011 .
JIANG Lijun. Reaearch on fatigue damage and creep damage properties of asphalt mixture under repeated loadings[D]. Changsha: Changsha University of Science & Technology, 2011. |
| [27] | LAGNEBORG R, ATTERMO R. The effect of combined low-cycle fatigue and creep on the life of austenitic stainless steel[J]. Metallurgical Transactions , 1971, 2 (7) : 1821-1827 |
| [28] |
谢锡善, 陈国良, 姜红根, 等. GH132合金盘材缺口对疲劳及蠕变/疲劳交互作用下的力学性能的影响[J].
北京科技大学学报 , 1989, 11 (2) : 130-135 XIE Xishan, CHEN Guoliang, JIANG Honggen, et al. Notch effect on fatigue and creep/fatigue interaction properties of GH132 disk superalloy[J]. Journal of University of Science and Technology Beijing , 1989, 11 (2) : 130-135 |
| [29] | MATT M.Guide for mechanistic-empirical design of new and rehabilitation pavement structure[R]. IIIinois, USA: National Cooperative Highway Research Board and National Research Council, 2004:12. |
| [30] |
张登良, 李俊. 高等级道路沥青路面车辙研究[J].
中国公路学报 , 1995, 8 (1) : 23-29 ZHANG Dengliang, LI Jun. Predietion of rutting in asphalt pavement[J]. China Journal of Highway and Transport , 1995, 8 (1) : 23-29 |
| [31] |
邓跃, 彭坤. 沥青路面车辙预估方法综述[J].
中外公路 , 2013, 33 (4) : 59-63 DENG Yue, PENG Kun. A review of asphalt pavement prediction method[J]. Journal of China & Foreign Highway , 2013, 33 (4) : 59-63 |
| [32] |
苏凯, 孙立军. 高等级沥青混凝土路面车辙预估方法研究综述[J].
公路 , 2006 (7) : 18-24 SU Kai, SUN Lijun. A summary of rutting prediction methodon high grade asphalt concrete pavements[J]. Highway , 2006 (7) : 18-24 |
| [33] |
付元坤. 沥青路面车辙预估模型的研究[D]. 西安: 长安大学, 2009.
FU Yuankun. Research on prediction model of asphalt pavement rut[D]. Xi′an: Chang′an University, 2009. |
| [34] | HILLS J F, BRIEN D, LOO P P. The correlation of rutting and creep tests on asphalt mixes, No. 1P 74-001 R&D Rpt[R]. London, UK: London Institute of Petroleum, 1974. |
| [35] | HUSCHEK S. Evaluation of rutting due to viscous flow in asphalt pavements[C]// Fourth International Conference of Structural Design of Asphalt Pavements.[S. l.]:[s. n.], 1977. |
| [36] | SOUSA J B, WEISSMAN S L, DEACON J A. Permanent pavement deformation response of asphalt aggregate mixes [R]. Washington D C, USA: SHRP National Research Council, 1994. |
| [37] |
徐世法, 朱照宏. 按黏弹性理论预估沥青路面车辙[J].
同济大学学报(自然科学版) , 1990, 18 (3) : 299-305 XU Shifa, ZHU Zhaohong. Prediction of rutting in asphalt pavements by using viscoelatic theory[J]. Journal of Tongji University(Natural Sciences) , 1990, 18 (3) : 299-305 |
| [38] | SHAMI H I. Development of temperature-effect model for predicting rutting of asphalt mixture using Georgia Loaded Wheel Test[R].Washington D C, USA: TRB, 1997. |
| [39] | ARCHILLA A R, MADANT S. A statistical model of pavement rutting in asphalt concrete mixes[C]// 80th Annual TRB Meeting. Washington D C, USA: Transportation Research Board, National Council, 2000. |
| [40] | KENIS W J. Predictive design proceduresa design method for flexible pavements using the Vesys structural subsystem. Proceedings[C]// 4th International Conference on the Structural Design of Asphalt Pavements. [S. l.]:[s. n.], 1977. |
| [41] | JACOB U. Prediction of rutting in asphalt pavements[J]. AAPT , 1983, 52489 |
| [42] | MONISMITH C L, DEACON J A, HARVEY J T. Westrackperformance models for permanent deformation and fatigue[M]. Berkeley, USA: Pavement Research Center, University of California, 2000 . |
| [43] | FWA T F, TAN S A, ZHU L Y. Rutting prediction of asphalt pavement layer using c-φ model[J]. Journal of Transportation Engineering, ASCE , 2004, 130 (5) : 675-683 DOI:10.1061/(ASCE)0733-947X(2004)130:5(675) |
| [44] | CAO W D, LIU ST, LI Y Y, et al. Rutting-resistance performance of SBS and anti-rutting additive composite-modified asphalt-concrete mixtures[J]. Journal of Testing and Evaluation , 2016, 44 (2) : 921-929 |
| [45] |
曹卫东, 冯志刚, 刘树堂, 等. 石灰岩与玄武岩集料SMA 高温蠕变特性试验研究[J].
山东大学学报(工学版) , 2013, 43 (2) : 70-75 CAO Weidong, FENG Zhigang, LIU Shutang, et al. Experimental research on high temperature creep property of stone matrixasphalt mixtures using basalt and limestone aggregates[J]. Journal of Shandong University (Engineering Science) , 2013, 43 (2) : 70-75 |
| [46] |
冯志刚. 重载交通混合式基层沥青路面超高温性能研究[D]. 济南:山东大学, 2014.
FENG Zhigang. Study on super high temperature performance of composite base asphalt pavement in heavy-duty traffic[D]. Jinan:Shandong University, 2014. |
| [47] | KRINGOS N, SCARPAS A. Physical and mechanical moisture susceptibility of asphaltic mixtures[J]. International Journal of Solids and Structures , 2008, 45 : 2671-2685 DOI:10.1016/j.ijsolstr.2007.12.017 |
| [48] | LU Q, JOHN T H. Investigation of conditions for moisture damage in asphalt concrete and appropriate laboratory test methods, Research Report: UCPRCRR-2005-15[R]. California, USA: University of California Transportation Center, 2005. |
| [49] | NGUYEN T, HUBBARD J, POMMERSHEIM J. Unified model for the degradation of organic coatings on steel in a neutral electrolyte[J]. Journal of Coatings Technology and Research , 1996, 68 (855) : 45-56 |
| [50] | NGUYEN T, MARTIN J, BYRD E. Relating laboratory and outdoor exposure of coatings:IV. mode and mechanism for hydrolytic degradation of acrylic melamine coatings exposed to water vapor in the absence of UV light[J]. Journal of Coatings Technology and Research , 2003, 75 (941) : 37-50 |
| [51] | NGUYEN T, BYRD E W, BENTZ D, et al. In situ spectroscopic study of water at the asphalt/siliceous substrate interface and its implication in stripping[J]. Journal of Adhesion , 2005, 81 (1) : 1-28 DOI:10.1080/00218460590904426 |
| [52] | AL-QADI I L, FINI E H, DESSOUKY S H. Adhesion of hot-poured crack sealants to aggregates[C]// 85th Annual Meeting of the Transportation Research Board. Washington D C, USA:[s. n.], 2006. |
| [53] | MERUSI F, CARUSO A, RONCELLA R, et al. Moisture susceptibility and stripping resistance of asphalt mixtures modified with different synthetic waxes[J]. Transportation Research Record Journal of the Transportation Research Board , 2010, 2180 (1) : 110-120 |
| [54] | CHENG D, LITTLE D N, LYTTON R L, et al. Moisture damage evaluation of asphalt mixtures by considering both moisture diffusion and repeated-load conditions[J]. Transportation Research Record Journal of the Transportation Research Board , 2003, 1832 (1) : 42-49 |
| [55] | ARABANI M, HAMEDI GH H. Using the surface free energy method to evaluate the effects of polymeric aggregate treatment on moisture damage in hot-mix asphalt[J]. Journal of Material Civil Engineering , 2010, 23 (6) : 802-811 |
| [56] | WASIUDDIN N M, FOGLE, CHRIS M, et al. Effect of antistrip additives on surface free energy characteristics of asphalt binders for moisture-induced damage potential[J]. Journal of Testing and Evaluation , 2007, 35 (1) : 36-44 |
| [57] | NETZEL D A. Apparent activation energies for molecular motions in solid asphalt[J]. Energy & Fuels , 2006, 20 (5) : 2181-2188 |
| [58] | PLANCHER H, DORRENCE S M, PETERSEN J C. Identification of chemical types in asphalts strongly adsorbed at the asphalt-aggregate interface and their relative displacement by water[J]. Association of Asphalt Paving Technologists , 1977, 46 : 151-175 |
| [59] | MEHRARA A, KHODAII A. A review of state of the art on stripping phenomenon in asphalt concrete[J]. Construction and Building Materials , 2013, 38 : 423-442 DOI:10.1016/j.conbuildmat.2012.08.033 |
| [60] | TARRERA R. Stripping of asphalt concretechemical testing, Report number 2, Project #930-111[R]. Alabama, USA:[s. n.], 1986. |
| [61] | LU Q, HARVEY J T. Inclusion of moisture effect in fatigue test for asphalt pavements[C]// The First International Symposium on Transportation and Development Innovation Best Practices (TDIBP 2008). [S. l.]:[s. n.], 2008. |
| [62] | RICE J M. Relationship of aggregate characteristics to the effect of water on bituminous paving mixtures[C]// Symposium on Effect of Water on Bituminous Paving Mixtures. Philadelphia, Boston, Massachusetts, USA:American Society for Testing Materials, 1958:17-34. |
| [63] | THELEN E. Surface energy and adhesion properties in asphalt-aggregate systems[J]. Highway Research Board Bulletin , 1958, 192 : 63-74 |
| [64] | KIGGUNDU B M, ROBERTS F L. Stripping in HMA mixtures: state-of-the-art and critical review of test methods, NCAT Report 88-2[R]. [S. l.]: National Center for Asphalt Technology, 1988. |
| [65] | D′ANGELO J, ANDERSON R. Material production, mix design, and pavement design effects on moisture damage[C]// Moisture Sensitivity of Asphalt Pavements-a National Seminar. San Diego, California, USA: Transportation Research Board, 2003:187-201. |
| [66] | STUART K D. Moisture damage in asphalt mixtures—state-of-the-art report, Report No. FHWA-RD-90-019 [R]. [S. l.]: Department of Transportation, Federal Highway Administration, 1990. |
| [67] | TERREL R L, AL-SWAILMI S. Water sensitivity of asphalt-aggregate mixestest selection, Strategic Highway research Program Report A-403[R]. Corvallis, USA: Oregon State University, 1994. |
| [68] | 崔新壮. 路面(病害)力学[M]. 北京: 科学出版社, 2015 . |
| [69] |
李少波, 张宏超, 孙立军. 动水压力的形成与模拟测量[J].
同济大学学报(自然科学版) , 2007, 35 (7) : 915-918 LI Shaobo, ZHANG Hongjun, SUN Lijun. Development and simulation measurement of dynamic hydraulic pressure[J]. Journal of Tongji University(Natural Science) , 2007, 35 (7) : 915-918 |
| [70] | CUI X Z, ZHANG J, ZHANG N, et al. Laboratory simulation tests of effect of mechanical damage on moisture damage evolution in hot-mix asphalt pavement[J]. International Journal of Pavement Engineering , 2015, 16 (8) : 699-709 DOI:10.1080/10298436.2014.943221 |
| [71] |
崔新壮, 金青, 张娜, 等. 损伤沥青混合料渗透性模型与水稳定性试验[J].
中国公路学报 , 2014, 27 (3) : 1-10 CUI Xinzhuang, JIN Qing, ZHANG Na, et al. Experiment on permeability model and water stability of damaged asphalt mixture[J]. China Journal of Highway and Transport , 2014, 27 (3) : 1-10 |
| [72] |
崔新壮, 金青. 轮载作用下饱水沥青路面的动力响应[J].
山东大学学报(工学版) , 2008, 38 (5) : 19-24 CUI Xinzhuang, JIN Qing. The dynamic response of saturated asphalt pavement under wheel loads[J]. Journal of Shandong University (Engineering Science) , 2008, 38 (5) : 19-24 |
| [73] | CUI X Z, CAO W D, LIU S, et al. On dynamic pore pressure in moisture damage of asphalt pavement[J]. Geotechnical Special Publication , 2009, 195 : 121-125 |
| [74] |
汤潍泽, 欧金秋, 崔新壮, 等. 车载引起的沥青路面内动水压力现场试验研究[J].
山东大学学报(工学版) , 2015, 45 (6) : 84-106 TANG Weize, OU Jinqiu, CUI Xinzhuang, et al. Field test and research on vehicle load induced dynamic pore pressure in asphalt pavement[J]. Journal of Shandong University (Engineering Science) , 2015, 45 (6) : 84-106 |
| [75] | GAO J Q, GUO C C, LIU Y T. Measurement of pore water pressure in asphalt pavement and its effects on permeability[J]. Measurement , 2015, 62 : 81-87 DOI:10.1016/j.measurement.2014.11.013 |
| [76] | 薛强, 盛谦. 沥青路面破坏的多场耦合效应及控制技术. 北京:科学出版社[M]. 2009 . |
| [77] |
吴国雄, 周宇, 杨锐. 降雨入渗时沥青路面流固耦合作用的力学响应[J].
重庆交通大学学报(自然科学版) , 2012, 31 (6) : 1141-1148 WU Guoxiong, ZHOU Yu, YANG Rui. Mechanical response of asphalt pavement under fluid-solid coupling in the case of rainfall infiltration[J]. Journal of Chongqing Jiaotong University (Natural Science) , 2012, 31 (6) : 1141-1148 |
| [78] |
邓融. 水和荷载耦合作用下沥青路面动力响应研究[D]. 大连:大连海事大学, 2010.
DENG Rong. Dynamic response of asphalt pavement subjected to the coupling action of moisture-loading[D]. Dalian:Dalian Maritime University, 2010. |
| [79] |
欧金秋. 沥青路面水损坏的动水压力驱动机理研究[D]. 济南:山东大学, 2012.
OU Jinqiu. Dynamic pore water pressure driving mechanism research of asphalt pavement moisture damage[D]. Jinan: Shandong University, 2012. |
| [80] | CUI X Z. Dynamic numerical analysis of antimoisture-damage mechanism of permeable pavement base[J]. International Journal of Geomechanics , 2010, 10 (6) : 230-235 DOI:10.1061/(ASCE)GM.1943-5622.0000030 |
| [81] |
李天祥, 李矗. 沥青路面抗滑性能衰减试验研究进展[J].
中国新技术新产品 , 2010 : 1863 LI Tianxiang, LI Chu. A review of the simulative test of skid resistance degradation of asphalt pavement surface[J]. China New Technologies and Products , 2010 : 1863 |
| [82] | DO M T, TANG Z, KANE M, et al. Evolution of road-surface skid-resistance and texture due to polishing[J]. Wear , 2009, 266 (5-6) : 574-577 DOI:10.1016/j.wear.2008.04.060 |
| [83] | HOLT F B, MUSGROVE G R. Surface texture classification: a guide to pavement skid resistance[J]. Pavement Surface Characteristics and Materials, ASTM STP , 1982, 763 : 31-44 |
| [84] | HOLM R. Electric contactstheory and application[M]. Heidelberg: Springer, 1967 . |
| [85] | BURWELL J T, STRANG C D. On the empirical law of adhesive wear[J]. Journal of Applied Physics , 1952, 23 (1) : 18-28 DOI:10.1063/1.1701970 |
| [86] | SUH N P. An overview of the delamination theory of wear[J]. Wear , 1977, 44 (1) : 1-16 DOI:10.1016/0043-1648(77)90081-3 |
| [87] | WILSON D J, DUNN R C M. Analyzing road pavement skid resistance[J]. Institute of Transportation Engineers , 2005 |
| [88] | 沙庆林. 高速公路沥青路面早期破坏现象及预防[M]. 北京: 人民交通出版社, 2003 . |
| [89] | KENNEDY C K, YOUNG A E, BUTLER I C. Measurement of skidding resistance and surface texture and the use of results in the United Kingdom[C]// Surface Characteristics of Roadways, International Research and Technologies: 1st Symposium on Surface Characteristics. State College, Pennsylvania, USA: ASTM, 1990:87-102. |
| [90] | HENRY J J. Evaluation of pavement friction characteristics[C]// National Cooperative Highway Research Program. Washington D C, USA: Transportation Research Board, 2000. |
| [91] | SMITH R H. Analyzing friction in the design of rubber products and their paired surfaces[M]. Florida, USA: CRC Press, 2008 . |
| [92] | LUO Y J. Effect of pavement temperature on frictional properties of hot-mix-asphalt pavement surfaces at the virginia smart road[D]. Virginia, USA: Virginia Polytechnic Institute, 2003. |
| [93] |
刘君. 单轮式横向力系数测试系统研究[J].
山西建筑 , 2011, 37 (27) : 148-149 LIU Jun. Study on the test system of single wheel type transverse force[J]. Shanxi Architecture , 2011, 37 (27) : 148-149 |
| [94] |
李长城, 刘小明, 荣建. 不同路面状况对路面摩擦系数影响的试验研究[J].
公路交通科技 , 2010, 27 (12) : 27-32 LI Changcheng, LIU Xiaoming, RONG Jian. Experimental study on effect of road condition on pavement friction coefficient[J]. Journal of Highway and Transportation Research and Development , 2010, 27 (12) : 27-32 |
| [95] | KHAN A M, BACCHUS A, HOLTZ N M. Multilane highway design crossfall and drainage issues[J]. Transportation Research Record , 1994 : 1-9 |
| [96] |
刘明智.环境因素对沥青路面抗滑性能影响研究[D].哈尔滨:哈尔滨工业大学, 2015.
LIU Mingzhi. Research of environmental factors on the asphalt pavement anti-sliding performance impact[D]. Harbin: Harbin Institute of Technology, 2015. |
| [97] | WILSON D J. The effect of rainfall and contaminants on road pavement skid resistance[R]. [S. l.]:New Zealand Transport Agency, 2013. |
| [98] |
肖鑫, 张起森, 关宏信. 交通荷载对沥青路面抗滑性能衰减规律的影响[J].
交通科学与工程 , 2011, 27 (3) : 6-10 XIAO Xin, ZHANG Qisen, GUAN Hongxin. The effect of traffic load on the attenuation of antiskid performance of asphalt pavement[J]. Journal of Transport Science and Engineering , 2011, 27 (3) : 6-10 |
| [99] |
孙洪利. 沥青路面抗滑性能衰减特性研究[J].
公路 , 2011 (7) : 73-78 SUNHongli. Study on the attenuation characteristic of asphalt pavement skid resistance performance[J]. Highway , 2011 (7) : 73-78 |
| [100] |
宫秀青. 沥青路面宏观纹理磨损与抗滑性能衰变行为研究[D]. 北京:北京工业大学, 2014.
GONG Xiuqing. Research on macrotexture wear and skid resistance degradation of asphalt pavement[D]. Beijing: Beijing University of Technology, 2014. |
| [101] |
李波, 徐欧明, 韩森. 路表纹理的分形表征及在抗滑性预估中的应用[J].
武汉理工大学学报 , 2009, 31 (19) : 102-104 LI Bo, XUOuming, HAN Sen. Fractal characterization of pavement texture and its application in skidding resistance prediction[J]. Journal of Wuhan University of Technology , 2009, 31 (19) : 102-104 |
| [102] | HOGERVORST D. Some properties of crushed stone for road surfaces[J]. Bulletin of the International Association of Engineering Geology , 1974, 10 (1) : 59-64 DOI:10.1007/BF02634635 |
| [103] |
杨众, 郭忠印, 侯芸. 沥青混凝土防滑磨耗层防滑性能加速试验方法的研究[J].
华东公路 , 2002, 135 (2) : 50-54 YANG Zhong, GUO Zhongyin, HOU Yun. Study on the acceleration test method of the skid resistance performance for the anti-skid wearing course of asphalt concrete pavement[J]. East China Highway , 2002, 135 (2) : 50-54 |
| [104] |
赵战利. 基于分形方法的沥青路面抗滑技术研究[D]. 西安:长安大学, 2005.
ZHAO Zhanli. Research on skid resistance technology of asphalt pavement based on fractal method[D]. Xi′an: Chang′an University, 2005. |
| [105] | Karol J, Kowalski, Rebecca S, et al. Long term monitoring of the noise and frictional properties of PFC, SMA and DGA pavements[R]. [S. l.]:[s. n.], 2009. |




