2. 山东劳动职业技术学院电气及自动化系,山东 济南 250100;
3. 山东女子学院信息技术学院,山东 济南 250100
2. Department of Electrics and Automation,Shandong Labor Vocational and Technical College,Jinan 250100,Shandong,China ;
3. College of Information Technology,Shandong Women′s University,Jinan 250100,Shandong,China
积分时滞过程是工业过程控制领域内常见的被控对象,当这类被控对象受到扰动后,输出参数很难自动稳定并重新恢复平稳,因而这类系统的控制难度较大[1-2]。文献[3采用二自由度串级控制结构,将设定值滤波器加入到主回路中,利用H∞优化方法设计主回路控制器,提高系统跟随性能,并采用内模控制方法设计副回路的2个控制器,取得了较好的控制效果。文献[4提出一种二自由度Smith预估控制方法,主回路采用二自由度Smith 预估控制结构,使系统设定值跟随性和干扰抑制特性解耦,副回路采用内模控制结构。其控制算法简单,易于工程应用。文献[5]提出了基于幅相裕度的PID参数整定方法,并针对一阶和二阶时滞系统仿真验证了该方法的有效性。文献[6-8]分别基于直接综合法、最大灵敏度指标和期望闭环性能指标,确定了积分时滞过程的PID控制器参数,但计算方法较繁琐。文献[9]采用ISE积分指标最小化方法整定PID调节器参数,提供了选择增益频率和奈奎斯特曲线的斜率准则,并成功应用于积分时滞过程,但系统动态响应较差。
考虑上述存在的问题,本研究将文献[10-11]的设计方法推广,提出了积分时滞过程的一种新的内模PID鲁棒控制方法。首先,对积分环节的处理,采用一阶环节逼近。然后,用一阶泰勒级数逼近对象中的纯滞后项,将时滞控制系统控制问题转化为非时滞系统控制问题。最后,基于鲁棒性能指标给出了简单的参数整定解析表达式。所设计的控制系统结构简单,参数整定方便,且在模型精度不高的情况下,仍然可以获得非常好的鲁棒性。
1 积分时滞对象的内模控制器设计考虑积分时滞过程模型
| ${{\tilde{G}}_{p}}\left( s \right)=\frac{K}{s}{{\tilde{G}}_{po}}\left( s \right){{e}^{-\theta s}}$ | (1) |
式中:
| ${{\tilde{G}}_{p}}\left( s \right)={{P}_{M}}\left( s \right){{P}_{A}}\left( s \right)$ | (2) |
式中:PM(s)为模型的可逆部分,是具有最小相位特征的传递函数;PA(s)为不可逆部分,其传递函数为全通滤波器,模型中所有的时滞和右半平面零点均在不可逆部分。
为保证系统的稳定性和鲁棒性,通常将一个滤波器增加在模型的最小相位部分,定义内模控制器
| ${{G}_{IMC}}=P_{M}^{-1}\left( S \right)f$ | (3) |
滤波器f通常采用
式中:nm≥0;β为常数;λ可以自由选择。如果Gp(s)≠Gp(s),即模型失配,在闭环系统稳定的前提下,只要设计内模控制器
将内模控制系统等效变换为常规反馈控制系统,得到内模控制器与反馈控制器之间的关系:
| ${{G}_{c}}\left( s \right)\approx \frac{{{G}_{IMC}}\left( s \right)}{1-{{G}_{IMC}}\left( s \right){{{\tilde{G}}}_{p}}\left( s \right)}.$ |
针对积分时滞对象特性,利用一阶环节逼近积分环节,即K/s≈αK/(αs+1),其中α取足够大,从而式(1)可以写为
| ${{G}_{c}}\left( s \right)\approx \frac{\alpha K}{\alpha s+1}{{\tilde{G}}_{po}}\left( s \right){{e}^{-\theta s}}$ |
由式(1)~(3)可得
| ${{G}_{IMC}}=\frac{\alpha s+1}{\alpha K{{{\tilde{G}}}_{po}}\left( s \right)}f,$ |
得IMC-PID控制器
| ${{G}_{c}}\left( s \right)=\frac{{{G}_{IMC}}\left( s \right)}{1-{{G}_{IMC}}\left( s \right){{{\tilde{G}}}_{p}}\left( s \right)}=\frac{\alpha s+1}{\alpha K{{{\tilde{G}}}_{po}}\left( s \right)\left( {{f}^{-1}}\left( s \right)-{{e}^{-\theta s}} \right)}.$ |
考虑一阶和二阶积分时滞过程模型为:
| ${{\tilde{G}}_{p}}\left( s \right)=\frac{K}{s}{{e}^{-\theta s}}\approx \frac{\alpha K}{\alpha s+1}{{e}^{-\theta s}},$ | (4) |
| ${{\tilde{G}}_{p}}\left( s \right)=\frac{K}{s\left( \tau s+1 \right)}{{e}^{-\theta s}}\approx \frac{\alpha k}{\left( \alpha s+1 \right)\left( \tau s+1 \right)}{{e}^{-\theta s}},$ | (5) |
式中τ为过程的时间常数。滤波器选取f=1/(λs+1),则系统反馈控制器分别为
| ${{G}_{c}}\left( s \right)=\frac{\alpha s+1}{\alpha K\left( 1+\lambda s-{{e}^{-\theta s}} \right)},$ | (6) |
| ${{G}_{c}}\left( s \right)=\frac{\left( \alpha s+1 \right)\left( \tau s+1 \right)}{\alpha K\left( 1+\lambda s-{{e}^{-\theta s}} \right)},$ | (7) |
用一阶泰勒表达式逼近式(6)(7)中的时滞项,即e-θs≈1-θs,得到内模PI和PID控制器的标准表达式
| ${{G}_{c}}\left( s \right)=\frac{1}{K\left( \lambda +\theta \right)}\left( 1+\frac{1}{\alpha s} \right),$ | (8) |
| ${{G}_{c}}\left( s \right)=\frac{\alpha +\tau }{\alpha K\left( \lambda +\theta \right)}\left[ 1+\frac{1}{\left( \alpha +\tau \right)s}+\frac{\alpha \tau }{\alpha +\tau }s \right].$ | (9) |
文献[11$提出的鲁棒性能指标γ为
| $\frac{1}{\gamma }=\underset{0\le \omega <\infty }{\mathop{max}}\,|\operatorname{Re}\left( {{G}_{c}}\left( j\omega \right){{{\tilde{G}}}_{p}}\left( j\omega \right) \right)|,$ | (10) |
式中:Gc(jω)为IMC-PID控制器频率特性;GP(jω)为过程模型的频率特性,系统开环传递频率特性GL(jw)=Gc(jw) GP(jw),即γ的值为GL(jω)实部最大绝对值的倒数。由式(10)分析,γ与幅值、相位裕度关系为
| $\left\{ \begin{array}{*{35}{l}} {{A}_{_{m}}}>\gamma ,\\ {{\phi }_{m}}>\arccos \frac{1}{\gamma },\\ \end{array} \right.$ |
式中:Am为系统幅值裕度; φm为相位裕度。可见,γ可以同时满足幅值、相位裕度的要求,其取值范围为1.5~2.5,其值越大,系统鲁棒性越好。
由式(4)(5)(8)和(9)可得:
| ${{G}_{L}}\left( s \right)=\frac{{{e}^{-\theta s}}}{\left( \lambda +\theta \right)s},$ |
| $|\operatorname{Re}{{G}_{L}}\left( j\omega \right)|=\left| -\frac{1}{\lambda +\theta }\centerdot \frac{\sin \omega \theta }{\omega } \right|,$ | (11) |
式(11)的最大值的计算式
| $\underset{\omega \to 0}{\mathop{\lim }}\,|=\underset{\omega \to 0}{\mathop{\lim }}\,|\left| -\frac{1}{\lambda +\theta }\centerdot \frac{\sin \omega \theta }{\omega } \right|=\frac{\theta }{\lambda +\theta }.$ | (12) |
由式(10)与(12)可得内模PID控制器可调参数λ与系统鲁棒性能指标γ之间的关系为
| $\lambda =\left( \gamma -1 \right)\theta .$ | (13) |
从式(13)可以看出,控制器可调参数λ可以由系统鲁棒性能指标γ的取值确定,避免了参数选择的盲目性。
4 仿真研究| ${{G}_{P1}}\left( s \right)=\frac{0.2}{s}{{e}^{-7.4s}},$ |
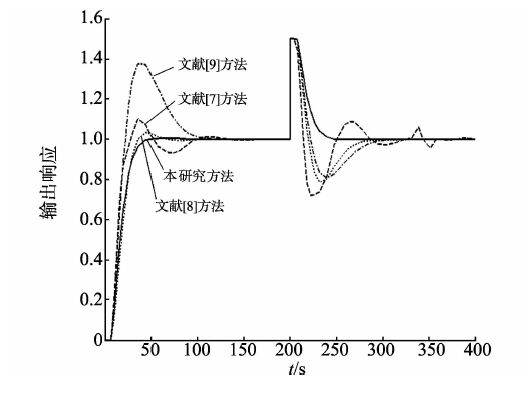
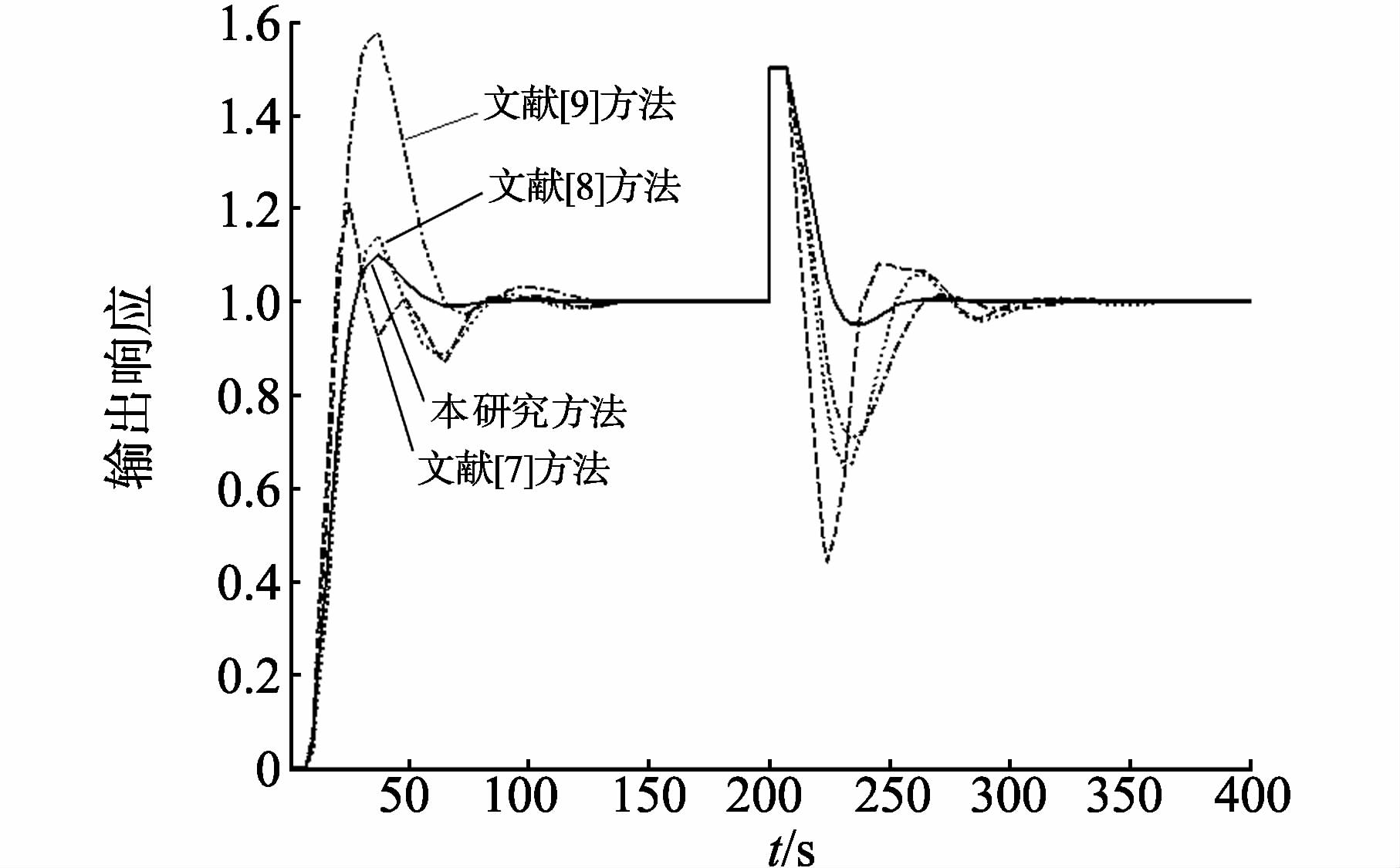
其中文献[7] 采用的是二自由度控制器设计方法,并基于最大灵敏度指标计算PID参数。文献[8-9]采用直接综合方法对时滞系统IMC-PI/PID参数进行整定。为保证比较的公平性,鲁棒性能指标γ均取2.5,文献[7-9]方法中的参数整定结果见文献[10],本研究中λ=(γ-1)θ=11.1,α取10000,进行控制器参数整定,利用式(8)可得Kp=0.27和Ti=10000。标称系统单位阶跃响应曲线如图 1所示,当t=200s时加入幅值为0.1的阶跃输入扰动,并利用时间乘以误差绝对值积分JITAE和超调量σ性能指标来验证系统闭环系统响应,如表 1所示。当过程模型产生+20%的误差时,即K=0.24,θ=8.88,系统输出单位阶跃响应曲线如图 2所示,可见本文方法具有较好的动态响应性能。
|
图 1 Gp1(s)系统阶跃响应曲线 Figure 1 Step response curves of Gp1(s) system |
| 表 1 Gp1(s)中不同控制方法性能比较 Table 1 Performance comparison of different controlmethods of Gp1(s) |
|
图 2 Gp1(s)模型失配时阶跃响应曲线 Figure 2 Step response curves of Gp1(s) system with model |
例 2 考虑二阶积分时滞过程
| ${{\tilde{G}}_{p2}}\left( s \right)=\frac{1}{s\left( s+1 \right)}{{e}^{-4s}},$ |
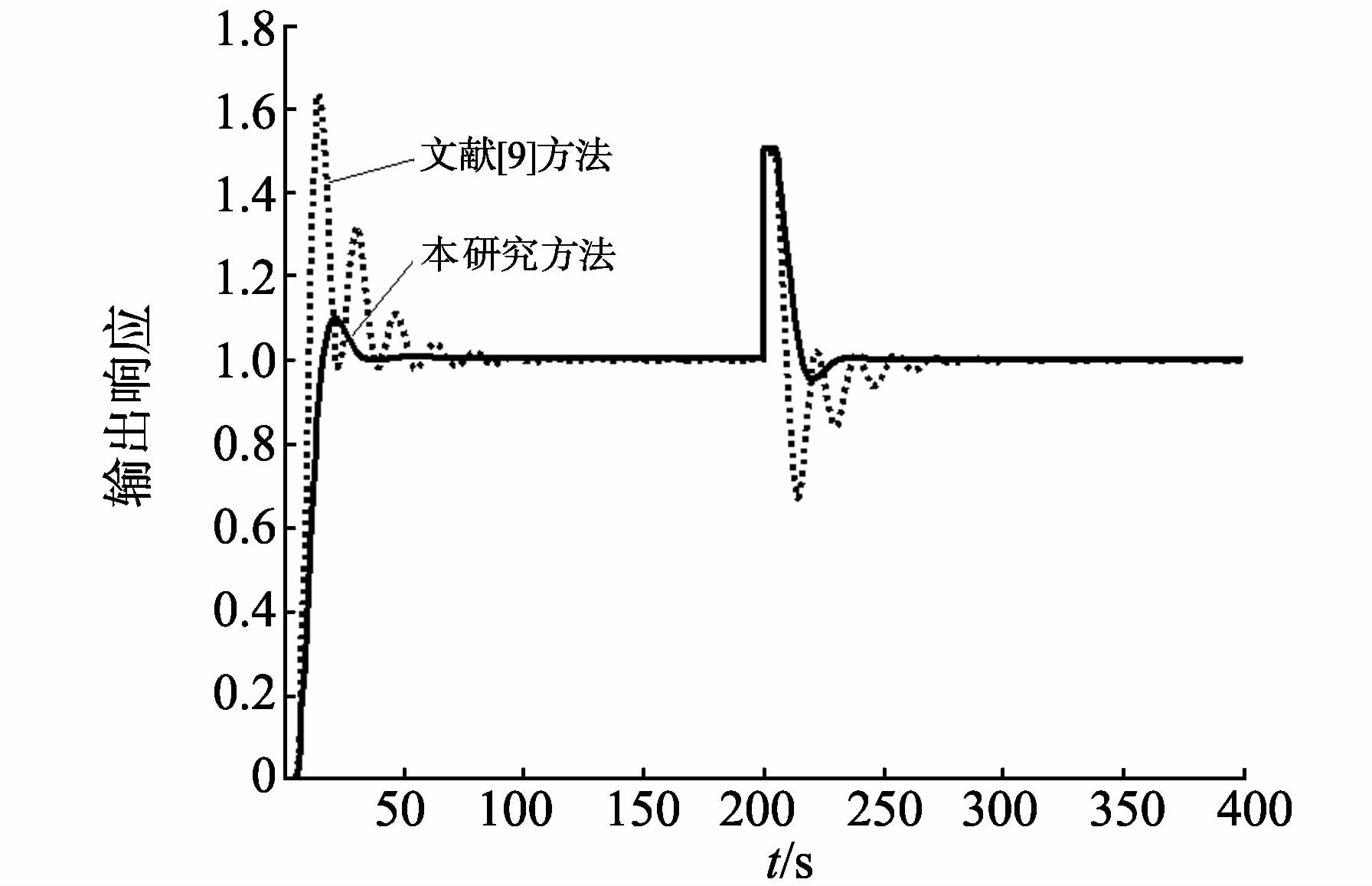
考虑到兼顾动态响应性能和鲁棒性而选择α=1000,γ=2.5。将本方法与文献[9]中的方案对比。在标称情况下,标称系统输出的单位阶跃响应如图 3所示。当t=200s时加入幅值为0.5的阶跃输入扰动。当过程模型产生+20%的摄动时,系统输出的单位阶跃响应如图 4所示。

|
图 3 Gp2(s)系统阶跃响应曲线 Figure 3 Step response curves of Gp2(s) system |
|
图 4 Gp2(s)模型失配阶跃响应 Figure 4 Step response curves of Gp2(s) system with model mismatch |
系统闭环系统响应由时间乘以误差绝对值积分JITAE和超调量σ性能指标来验证,如表 2所示。文献[9]方法使得系统的JITAE指标略小于本研究方法,但其超调量过大,本研究方法在抑制扰动时,系统输出响应几乎没有超调。可见本研究的控制方法能使系统保持良好的鲁棒性。
| 表 2 Gp2(s)采用不同控制方法性能比较 Table 2 Performance comparison of different controlmethods of Gp2(s) |
本研究针对积分时滞对象,给出了一种内模PID控制器的鲁棒整定方法。采用一阶环节逼近积分环节,用一阶泰勒级数逼近对象中的纯滞后项,推导得到IMC-PID控制器参数的设计公式,并基于鲁棒性能指标给出了简单的参数整定解析表达式。该方法结构简单、参数整定计算方便。仿真实例验证表明,所提出方法可以兼顾系统的设定值跟踪能力和抗负荷扰动能力,且具有良好的鲁棒稳定性。
| [1] | ALACNTARA S, ZHANG Weidong, PEDRET C, et al. IMC-like analytical H∞ design with S/SP mixed sensitivity consideration:utility in PIDtuning guidance[J]. Journal of Process Control , 2011, 21 (6) : 976-985 DOI:10.1016/j.jprocont.2011.04.007 |
| [2] | ZHAO Zhicheng, LIU Zhiyuan, ZHANG Jinggang. IMC-PID tuning method based on sensitivity specification for process with timedelay[J]. Journal of Central South University of Technology , 2011, 18 (4) : 1153-1160 DOI:10.1007/s11771-011-0817-0 |
| [3] | YIN Chengqiang, HUI Hongzhong, YUE Jiguang, et al. Cascade control based on minimum sensitivity in outer loop for processes with time delay[J]. Journal of Central South University , 2012, 19 (9) : 2689-2696 DOI:10.1007/s11771-012-1328-3 |
| [4] |
张井岗, 马文廷, 赵志诚. 串级时滞过程的二自由度Smith预估控制[J].
山东大学学报(工学版) , 2015, 45 (5) : 43-50 ZHANG Jinggang, MA Wenting, ZHAO Zhicheng. Two-degree-of-freedom Smith predictor control for cascade time delay process[J]. Journal of Shandong University(Engineering Science) , 2015, 45 (5) : 43-50 |
| [5] | LI Keyu. PID tuning for optimal closed-loop performance with specifiedgain and phase margins[J]. IEEE Trans on Control Systems Technology , 2013, 21 (3) : 1024-1030 DOI:10.1109/TCST.2012.2198479 |
| [6] | RAO A S, RAO V S R, CHIDAMBRAM M. Direct synthesis-based controller design for integrating processes with time delay[J]. Journal of the Franklin Institute , 2009, 346 (1) : 38-56 DOI:10.1016/j.jfranklin.2008.06.004 |
| [7] | SHAMSUZZOHA M, LEE M. IMC-PID controller design for improved disturbance rejection of time-delayed process[J]. Ind Eng Chem Res , 2007, 46 (7) : 2077-2091 DOI:10.1021/ie0612360 |
| [8] | CHEN Dan, SEBORG D E. PI/PID controller designbased on direct synthesis and disturbance rejection[J]. Ind Eng Chem Res , 2002, 41 (19) : 4807-4822 DOI:10.1021/ie010756m |
| [9] | AHMAD Ali, SOMANATH Majhi. PID controller tuning for integrating processes[J]. ISA Transactions , 2010, 49 (1) : 70-78 DOI:10.1016/j.isatra.2009.09.001 |
| [10] |
赵志诚, 刘志远, 张井岗. 一种时滞过程内模PID控制器鲁棒整定方法[J].
信息与控制 , 2010, 39 (5) : 526-530 ZHAO Zhicheng, LIU Zhiyuan, ZHANG Jinggang. A robust tuning method of internal model PID controller for process with time-delay[J]. Information and Control , 2010, 39 (5) : 526-530 |
| [11] | WANG Yagang, SHAO Huihe. PID auto-tuner based on sensitivity specification[J]. Chemical Engineering Research and Design , 2000, 78 (2) : 312-316 DOI:10.1205/026387600527176 |


