机械手是一个典型的具有未建模动态、摩擦作用、弹性力和耦合作用等不确定性的非线性系统[1-2]。随着机器人技术的发展,在工业自动化中领域,涂装和焊接等许多复杂的任务都交由能实现高精度轨迹跟踪的机械手来完成[3]。在负荷变动较大的情况下,为了实现机械手大范围运动的精确轨迹跟踪,许多先进控制方法,例如反馈线性化[4]、 模型预测控制[5]、 智能控制[6]、 自适应控制[7]、 滑模控制[8-11]等被应用到机械手的运动控制中。滑模控制因其方法简单、内在的鲁棒性而倍受青睐[9-10]。滑模控制通过不连续反馈控制律,能迫使系统状态运动到滑动模态,这种模态对系统不确定性具有不变性,是实现不确定非线性系统跟踪控制的最佳方法之一,已在机器人、过程控制、航空航天、电力系统等领域[11-12]获得广泛应用。
传统滑模控制的滑模切换面是线性的,系统状态是渐进收敛的,尽管可以通过调节线性滑模参数使得收敛速度加快,但是这种收敛仍是在无限时间内完成的[13]。在高精度的机械手运动控制中,需要较大的控制输入才能实现更快的收敛速度,但常会导致执行器输出饱和。终端滑模控制通过利用非线性滑模面,在较小的控制作用下亦能实现状态快速收敛。文献[14]将关节电机转角和柔性模态变量的线性组合作为柔性机械手系统的输出,通过输入输出线性化,将系统分解为输入输出子系统和零动态子系统两部分.针对输入输出子系统,提出了快速终端滑模控制策略,使得输入输出子系统在有限时间内收敛;Maolin Jin等人提出了一种二关节机械手的实际非奇异终端滑模控制方法[15];文献[16]结合径向基神经网络设计机械手终端滑模控制器,实现了对给定轨迹的跟踪;文献[17]提出了一种连续有限时间机械手控制方案,通过设计非奇异终端滑模,选择适当的分数幂,解决了终端滑模的奇异问题。但上述终端滑模控制存在两个缺点:一是可能激发系统未建模高频振荡的抖振现象,二是必须知道系统的不确定性上界。
为此,本研究针对一类MIMO(multiple-input multiple-output)非线性系统设计了一种自适应二阶终端滑模控制器,采用非奇异终端滑模面设计控制律,控制信号的时间导数作为新的控制输入,因为存在符号函数,该控制输入是不连续的,但经过积分所得的实际控制输入是连续的,因此抖振大大削弱。自适应调节律可估计未知不确定性,因此该自适应调节方法无需预先知道系统的不确定上界。将该控制方法应用于机械手轨迹跟踪控制中,仿真结果验证了其有效性。
1 自适应终端滑模控制器考虑一类MIMO不确定非线性系统
| $\dot{x}=f\left( x \right)+\Delta f\left( x \right)+gu+d\left( t \right),$ | (1) |
式中:x=[x1,x2,x3,…,xn]T∈Rn是状态向量; Δf(x)表示式(1)系统未建模动态或结构变化; g∈Rn×m是已知矩阵; u∈Rm是控制输入; d(t)∈Rn是外部干扰。假设系统不确定性有界并且满足匹配条件,控制目标是在任意初始状态,有限时间内跟踪给定参考信号xd=[x1d,x2d,x3d,…,xnd]T。
跟踪误差定义为
| $e=x-{{x}_{d}}={{\left[ {{x}_{1}}-{{x}_{1d}},{{x}_{2}}-{{x}_{2d}},{{x}_{3}}-{{x}_{3d}},\ldots ,{{x}_{n}}-{{x}_{nd}} \right]}^{T}}$ | (2) |
控制目标是设计终端滑模控制器,使得
| $\underset{t\to \infty }{\mathop{\lim }}\,\left\| e \right\|=\underset{t\to \infty }{\mathop{\lim }}\,\left\| x-{{x}_{d}} \right\|\to 0,$ | (3) |
式中‖·‖表示欧氏范数。
设计过程分为两步。
步骤 1 定义滑模面
| $\eqalign{ & \sigma = {[{\sigma _1},{\sigma _2}, \ldots ,{\sigma _m}]^T} = {c^T}e = {\left[ {{c_1},{c_2}, \ldots ,{c_i}, \ldots ,{c_m}} \right]^T}e \cr & = \left[ {\matrix{ {{c_{1n}}{e_n} + {c_{1(n - 1)}}{e_{n - 1}} + \ldots + {c_{11}}{e_1}} \cr {{c_{2n}}{e_n} + {c_{2(n - 1)}}{e_{n - 1}} + \ldots + {c_{21}}{e_1}} \cr \vdots \cr {{c_{mn}}{e_n} + {c_{m(n - 1)}}{e_{n - 1}} + \ldots + {c_{m1}}{e_1}} \cr } } \right], \cr} $ | (4) |
式中 ci=[cin,ci(n-1),…,ci1]T是多项式(5)在左半开平面所有可能的根。
| $\Phi (\lambda ({{e}_{i}}))={{c}_{in}}{{\lambda }^{n-2}}+{{c}_{i(n-1)}}{{\lambda }^{n-1}}+\ldots +{{c}_{i1}}\lambda $ | (5) |
式中i=1,2,…,m。c的选择决定了收敛到滑模面的速度。对式(4)求一阶时间导数
| $\dot{\sigma }={{c}^{T}}\dot{e}={{c}^{T}}(\dot{x}-{{{\dot{x}}}_{d}})$ | (6) |
由式(1)和式(6)得:
| $\dot{\sigma }={{c}^{T}}(f\left( x \right)+\Delta f\left( x \right)+d\left( t \right)+gu-{{{\dot{x}}}_{d}})$ | (7) |
对式(7)求导数:
| $\ddot{\sigma }={{c}^{T}}(\dot{f}\left( x \right)+\Delta \left( x \right)+\left( t \right)+g-{{{\dot{x}}}_{d}})$ | (8) |
步骤2设计非奇异终端滑模面
| $s=\sigma +\beta {{{\dot{\sigma }}}^{p/q}}$ | (9) |
式中: β=diag(β1,β2,…,βn)是正常数;p、q是正奇数并且满足1<p/q <2。线性滑模面σ与非奇异终端滑模面s结合实现终端滑模控制。因为s在有限时间内到达零,σ和${\dot{\sigma }}$必定会到达零,跟踪误差e会渐近收敛到零。
式(9)的时间导数为
| $\dot{s}=\dot{\sigma }+\beta {{{\dot{\sigma }}}^{p/q-1}}\ddot{\sigma }=\beta \frac{p}{q}{{{\dot{\sigma }}}^{p/q-1}}\left( \ddot{\sigma }+{{\beta }^{-1}}{{\left( \frac{p}{q} \right)}^{-1}}{{{\dot{\sigma }}}^{2-(p/q)}} \right)$ | (10) |
把式(8)代入式(10)得:
| $\begin{align} & \dot{s}~=\beta \left( \frac{p}{q} \right){{{\dot{\sigma }}}^{p/q-1}} \\ & \left( {{c}^{T}}(\dot{f}\left( x \right)+\Delta \dot{f}\left( x \right)+\dot{d}\left( t \right)+g\dot{u}-{{{\ddot{x}}}_{d}})+{{\beta }^{-1}}{{\left( \frac{p}{q} \right)}^{-1}}{{{\dot{\sigma }}}^{2-(p/q)}} \right) \\ \end{align}$ | (11) |
假设 1 Δ${\dot{f}}$(x),${\dot{d}}$(t)有界且满足:
| $\left\| \Delta \dot{F}\left( x \right) \right\|=\left\| {{c}^{T}}\left( \Delta \dot{f}\left( x \right)+d\left( t \right) \right) \right\| <\sum\limits_{i=0}^{r}{{{{\bar{B}}}_{i}}}{{\left\| x \right\|}^{i}},r=0,1,\ldots ,n,$ | (12) |
式中,Bi是未知正常数,在实际控制系统中,由于不确定项结构复杂,Bi的值不易获得; r是设计者根据系统可能受扰动的相对阶确定。设计传统滑模控制器时,通常假设复合扰动上界满足一定条件,例如,r=0,干扰是周期性的,其值可由已知常数表示,r=1时,包含更多的干扰类型。
定理1给出自适应二阶终端滑模控制器,其控制输入为控制信号的积分值,是连续的,可大大削弱抖振,系统的不确定上界值可由自适应调节律估计。
定理 1 考虑不确定系统(1),如果非奇异终端滑模面选取为式(9),并且控制律设计为
| $u={{u}_{eq}}+{{u}_{swt}}$ | (13) |
跟踪误差动态式(6)能够渐进收敛到零。其中:ueq是滑模控制中等效控制部分,迫使状态轨迹滑动到滑模面; uswt是滑模切换控制,在干扰存在时,维持滑模运动。
${\dot{u}}$eq由${\dot{s}}$=0求得:
| ${{{\dot{u}}}_{eq}}=-{{({{c}^{T}}g)}^{-1}}\left[ {{c}^{T}}\dot{f}\left( x \right)-{{c}^{T}}{{{\ddot{x}}}_{d}}+{{\beta }^{-1}}{{\left( \frac{p}{q} \right)}^{-1}}^{2-(p/q)} \right]$ | (14) |
| ${{u}_{eq}}=-{{({{c}^{T}}g)}^{-1}}\int_{0}^{t}{\left[ {{c}^{T}}\dot{f}\left( x \right)-{{c}^{T}}{{{\ddot{x}}}_{d}}+{{\beta }^{-1}}{{\left( \frac{p}{q} \right)}^{-1}}{{{\dot{\sigma }}}^{2-(p/q)}} \right]}d\zeta $ | (15) |
| ${{{\dot{u}}}_{swt}}=-{{({{c}^{T}}g)}^{-1}}\left[ \left( {{{\bar{B}}}_{0}}+{{{\bar{B}}}_{1}}\left\| x \right\| \right)sign\left( s \right)+\varepsilon s \right],$ | (16) |
| ${{u}_{swt}}=-{{({{c}^{T}}g)}^{-1}}\int_{0}^{t}{\left[ \left( {{{\bar{B}}}_{0}}+{{{\bar{B}}}_{1}}\left\| x \right\| \right)sign\left( s \right)+\varepsilon s \right]}d\zeta ,$ | (17) |
式中,cTg是非奇异的; B0,B1和ε=diag(ε1…εm)是设计参数。
实际应用中,不确定项(B0+B1‖x‖)的界通常是未知的,因此设计自适应律来估计B0和B1,控制律进一步表示为:
| $\left\{ \begin{matrix} u={{u}_{eq}}+{{u}_{swt}}, \\ {{u}_{eq}}=-{{({{c}^{T}}g)}^{-1}}\int_{0}^{t}{\left[ {{c}^{T}}\dot{f}\left( x \right)-{{c}^{T}}{{{\ddot{x}}}_{d}}+{{\beta }^{-1}}{{\left( \frac{p}{q} \right)}^{-1}}{{{\dot{\sigma }}}^{2-(p/q)}} \right]}d\zeta , \\ {{u}_{swt}}=-{{\left( {{c}^{T}}g \right)}^{-1}}\int_{0}^{t}{[({{{\hat{\bar{B}}}}_{0}}+\text{ }{{{\hat{\bar{B}}}}_{1}}\left\| x \right\|)sign\left( s \right)+\varepsilon s]d\zeta ,} \\ \end{matrix} \right.$ | (18) |
式中,B0e与B1e用来估计B0与B1的上界并且满足假设1,‖cT(Δ${\dot{f}}$(x)+d(t))‖ <B0+B1‖x‖。定义自适应误差0=B0e-${\tilde{\bar{B}}}$0,${\tilde{\bar{B}}}$1=B1e-1。B0e,B1e由以下自适应律估计:
| ${{B}_{0e}}=\frac{1}{{{\nu }_{0}}}\left( \frac{p}{q} \right)\left\| \beta \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|,$ | (19) |
| ${{B}_{1e}}=\frac{1}{{{\nu }_{1}}}\left( \frac{p}{q} \right)\left\| \beta \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|\left\| x \right\|,$ | (20) |
式中,ν0和ν1是正调节参数。
证明 考虑如下Lyapunov函数:
| $V\left( t \right)=\frac{1}{2}{{s}^{T}}s+\frac{1}{2}{{\mu }_{0}}~\tilde{\bar{B}}~_{0}^{2}+\frac{1}{2}{{\mu }_{1}}~\tilde{\bar{B}}_{1}^{2}~$ | (21) |
结合式(8),(10)和(15),V(t)的时间导数为
| $\begin{align} & \dot{V}~\left( t \right)={{s}^{T}}\dot{s}+{{\mu }_{0}}\tilde{\bar{B}}{{~}_{0}}{{{\dot{B}}}_{0e}}+{{\mu }_{1}}~{{{\tilde{\bar{B}}}}_{1}}{{{\dot{B}}}_{1e}}=\beta \frac{p}{q}{{{\dot{\sigma }}}^{\left( p/q \right)-1}}{{s}^{T}} \\ & \ddot{\sigma }+{{\beta }^{-1}}{{\left( \frac{p}{q} \right)}^{-1}}{{{\dot{\sigma }}}^{2-(p/q)}}+{{\mu }_{0}}\left( {{B}_{0e}}-{{{\bar{B}}}_{0}} \right){{{\dot{B}}}_{0e}}+{{\mu }_{1}}\left( {{B}_{1e}}-{{{\bar{B}}}_{1}} \right){{{\dot{B}}}_{1e}} \\ \end{align}$ | (22) |
结合式(13)~(16)得:
| $\begin{align} & \dot{V}\left( t \right)=\beta {{\frac{p}{q}}^{\left( p/q \right)-1}}{{\sigma }^{T}}\left[ {{c}^{T}}\left( \frac{d}{dt}\text{ }f\left( x \right)+\underbrace{\frac{d}{dt}\Delta f\left( x \right)+\dot{d}\left( t \right)}_{{{c}^{-T}}\Delta \dot{F}\left( x \right)}+g\dot{u}-{{{\ddot{x}}}_{d}} \right)+{{\beta }^{-1}}{{\frac{p}{q}}^{-1}}{{{\dot{\sigma }}}^{2-(p/q)}} \right]+ \\ & ~{{\mu }_{0}}\nu _{0}^{-1}\left( {{B}_{0e}}-{{{\bar{B}}}_{0}} \right)\left( \frac{p}{q} \right)\beta \left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|+{{\mu }_{1}}\nu _{1}^{-1}~\left( {{B}_{0e}}_{1}-{{{\bar{B}}}_{1}} \right)\left( \frac{p}{q} \right)\beta \left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|\left\| x \right\| \\ \end{align}$ | (23) |
结合式(15),(12)得:
| $\begin{align} & \dot{V}\left( t \right)=\beta \frac{p}{q}{{{\dot{\sigma }}}^{\left( p/q \right)-1}}{{s}^{T}}\left[ \Delta F\left( x \right)-\varepsilon s-\left( {{B}_{0e}}+{{B}_{1e}}\|x\| \right)sign\left( s \right) \right]+~ \\ & {{\mu }_{0}}{{\nu }^{-1}}_{0}~\left( {{B}_{0e}}-{{{\bar{B}}}_{0}} \right)\left( \frac{p}{q} \right)\left\| \beta \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|+{{\mu }_{1}}\nu _{1}^{-1}~\left( {{B}_{1e}}-{{{\bar{B}}}_{1}} \right)\left( \frac{p}{q} \right)\left\| \beta \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|\left\| x \right\| \\ \end{align}$ | (24) |
| $\begin{align} & \dot{V}\left( t \right)\le \left\| \beta \right\|\left( \frac{p}{q} \right)\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|\left[ \left\| \Delta F\left( x \right) \right\| \right.\left\| s \right\|-\left\| ({{B}_{0e}}+{{B}_{1e}}\left\| x \right\|) \right\|\left\| s \right\|+~ \\ & {{\mu }_{0}}\nu _{0}^{-1}\left\| ~\left( {{B}_{0e}}-{{{\bar{B}}}_{0}} \right) \right\|\left\| s \right\|+{{\mu }_{1}}{{\nu }^{-1}}_{1}~\left\| \left( {{B}_{1e}}-{{{\bar{B}}}_{1}} \right) \right\|\left. \left\| s \right\|\left\| x \right\| \right] \\ \end{align}$ | (25) |
| $\begin{align} & \dot{V}\left( t \right)\le \left\| \Delta F\left( x \right) \right\|\left\| s \right\|-\left\| \left( {{B}_{0e}}+{{B}_{1e}}\left\| x \right\| \right) \right\|\left\| s \right\|-\text{ } \\ & \left( \left\| {{B}_{1e}}-{{{\bar{B}}}_{0}} \right\| \right)\left\| s \right\|+{{\mu }_{0}}\nu _{0}^{-1}~\left( \left\| {{B}_{1e}}-{{{\bar{B}}}_{0}} \right\| \right)\left\| s \right\|+{{\mu }_{1}}\nu _{1}^{-1}~\left\| \left( {{B}_{1e}}-{{{\bar{B}}}_{1}} \right) \right\|\left\| s \right\|\left\| x \right\| \\ \end{align}$ | (26) |
| $\begin{align} & \dot{V}\left( t \right)\le -[\left\| \left( {{{\bar{B}}}_{0}}+{{{\bar{B}}}_{1}}\left\| x \right\| \right) \right\|-\left\| \Delta \dot{F}\left( x \right) \right\|]\left\| s \right\|-\left\| \left( {{B}_{0e}}-{{{\bar{B}}}_{0}} \right) \right\|\left( \left\| s \right\|-{{\mu }_{0}}\nu _{0}^{-1}\left\| s \right\| \right)- \\ & \left\| \left( {{B}_{1e}}-{{{\bar{B}}}_{1}} \right) \right\|(\left\| s \right\|\left\| x \right\|-{{\mu }_{0}}\nu _{0}^{-1}~\left\| s \right\|\left\| x \right\|)\le \\ & -{{\beta }_{\sigma }}\sqrt{2}\frac{\left\| s \right\|}{\sqrt{2}}-{{\beta }_{\gamma }}\sqrt{2\mu _{0}^{-1}}~\left\| {{{\tilde{\bar{B}}}}_{0}} \right\|\sqrt{\frac{{{\mu }_{0}}}{2}}-{{\beta }_{\delta }}2\mu _{1}^{-1}~\left\| {{{\tilde{\bar{B}}}}_{1}} \right\|\sqrt{\frac{{{\mu }_{1}}}{2}} \\ \end{align}$ | (27) |
式中,βσ=‖(B0+B1‖x‖)‖-‖Δ${\dot{F}}$(x)‖; βγ=(‖s‖-μ0ν0-1 ‖s‖); βδ=(‖s‖-μ0ν0 -1‖s‖)‖x‖。因此,当${\dot{B}}$0e=(1/ν0)(p/q)‖β‖‖${\dot{\sigma }}$(p/1)-1s‖,${\dot{B}}$1e=(1/ν1)(p/q)‖β‖‖${\dot{\sigma }}$(p/q)-1s‖‖x‖,{‖(B0+B1‖x‖)‖-‖Δ${\dot{F}}$(x)‖}>0,μ0ν0-1 <1,μ1ν1-1 <1成立,有
| $\begin{align} & \dot{V}\left( t \right)\le -min\left\{ \sqrt{2} \right.{{\beta }_{\sigma }},{{\beta }_{\gamma }}\sqrt{2\mu _{0}^{-1}}~,{{\beta }_{\delta }}\left. \sqrt{2\mu _{1}^{-1}~} \right\} \\ & \frac{\left\| s \right\|}{\sqrt{2}}+\sqrt{\frac{{{\mu }_{0}}}{2}}\left\| {{{\tilde{\bar{B}}}}_{0}} \right\|+\sqrt{\frac{{{\mu }_{1}}}{2}}\left\| {{{\tilde{\bar{B}}}}_{1}} \right\|\le -{{\beta }_{c}}{{V}^{1/2}}\left( t \right), \\ \end{align}$ | (28) |
式中,
注 1 当‖s‖=0可达到时,上述方法是适用的,但在实际的滑模控制中,由于非线性和切换的滞后性,‖s‖并不能在有限时间内精确为零,因此自适应参数B0e,B1e可能会无限的变大,利用如下死区技术调整自适应调节律可以解决这个问题[18-19]。
| ${{B}_{0e}}=\left\{ \begin{matrix} \frac{1}{{{\nu }_{0}}}\left( \frac{p}{q} \right)\left\| \beta \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|, & \left\| s \right\|\ge \zeta ; \\ 0, & \left\| s \right\| <\zeta \\ \end{matrix} \right.$ | (29) |
| ${{B}_{1e}}=\left\{ \begin{matrix} \frac{1}{{{\nu }_{1}}}\left( \frac{p}{q} \right)\left\| \beta \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|\left\| x \right\|, & \left\| s \right\|\ge \zeta ; \\ 0, & \left\| s \right\| <\zeta \\ \end{matrix} \right.$ | (30) |
式中ζ是小的正常数。
2 机械手轨迹跟踪自适应终端滑模控制器设计| $M\left( q \right)\ddot{q}+C\left( q,\dot{q} \right)\dot{q}+G\left( q \right)=\tau +{{\tau }_{d}},$ | (31) |
式中,q、${\dot{q}}$、${\ddot{q}}$分别表示关节的位置、速度、加速度;M(q)=M0(q)+ΔM(q)∈Rn×n是机械手惯性矩阵;C(q,${\dot{q}}$)=C0(q,${\dot{q}}$)+ΔC(q,${\dot{q}}$)∈Rn×n是离心力和哥氏力;G(q)=G0(q)+ΔG(q)∈Rn表示重力项;τ∈Rn是控制力矩;τd是干扰力矩向量;M0(q),C0(q,${\dot{q}}$),G0(q)是标称值;ΔM(q)、ΔC(q,${\dot{q}}$)、ΔG(q)表示系统矩阵摄动。则机械手动态模型可写为
| ${{M}_{0}}\left( q \right)\ddot{q}+{{C}_{0}}\left( q,\dot{q} \right)\dot{q}+{{G}_{0}}\left( q \right)=\tau +{{\tau }_{d}}+F\left( q,\dot{q},\ddot{q} \right)$ | (32) |
式中,F(q,${\dot{q}}$,${\ddot{q}}$)=-ΔM(q)-ΔC(q,${\dot{q}}$)-ΔG(q)∈Rn是系统复合不确定性,满足
| $\left\| F\left( q,\dot{q},\ddot{q} \right) \right\|<{{\rho }_{0}}+{{\rho }_{1}}\left\| q \right\|+{{\rho }_{2}}{{\left\| {\dot{q}} \right\|}^{2}}$ | (33) |
式中ρ0、 ρ1、 ρ2是正常数。
控制目标是使得机械手跟踪参考轨迹,定义qd和q是期望的和实际的位置矢量,跟踪误差及其导数定义为:e=qd-q,${\dot{e}}$=${\dot{q}}$d-${\dot{q}}$,${\ddot{e}}$=${\ddot{q}}$d-${\ddot{q}}$,结合式(32),得
| $\ddot{e}=M_{0}^{-1}\left( q \right)[\tau +{{\tau }_{d}}+F\left( q,\dot{q},\ddot{q} \right)-{{C}_{0}}\left( q,\dot{q} \right)+{{G}_{0}}\left( q \right)]-{{{\ddot{q}}}_{d}}$ | (34) |
对式(34)求导数:
| $\begin{align} & \frac{d}{dt}\ddot{e}=\text{ }M_{0}^{-1}~\left( q \right)\left[ \dot{\tau }+{{{\dot{\tau }}}_{d}}+\dot{F}\left( q,\dot{q},\ddot{q} \right)-\frac{d}{dt}({{C}_{0}}\left( q,\dot{q} \right)\dot{q}+{{G}_{0}}\left( q \right)) \right]+~ \\ & {{{\dot{M}}}^{-1}}_{0}~\left( q \right)[\tau +{{\tau }_{d}}+F\left( q,\dot{q},\ddot{q} \right)-{{C}_{0}}\left( q,\dot{q} \right)\dot{q}+{{G}_{0}}\left( q \right)]-\frac{d}{dt}{{{\ddot{q}}}_{d}}=\text{ } \\ & M_{0}^{-1}\left( q \right)\left[ \dot{\tau }-\frac{d}{dt}({{C}_{0}}\left( q,\dot{q} \right)\dot{q}+{{G}_{0}}\left( q \right)) \right]+{{{\dot{M}}}^{-1}}_{0}~\left( q \right)[\tau -{{C}_{0}}\left( q,\dot{q} \right)\dot{q}-{{G}_{0}}\left( q \right)]-\frac{d}{dt}{{{\ddot{q}}}_{d}}+\text{ } \\ & M_{0}^{-1}~\left( q \right){{{\dot{\tau }}}_{d}}+M_{0}^{-1}~\left( q \right)+\dot{F}\left( q,\dot{q},\ddot{q} \right)+\dot{M}_{0}^{-1}\left( q \right){{\tau }_{d}}+\dot{M}_{0}^{-1}~\left( q \right)F\left( q,\dot{q},\ddot{q} \right)=\text{ } \\ & M_{0}^{-1}~\left( q \right)\left[ \dot{\tau }-\frac{d}{dt}({{C}_{0}}\left( q,\dot{q} \right)\dot{q}+{{G}_{0}}\left( q \right)) \right]+\dot{M}_{0}^{-1}\left( q \right)[\tau -{{C}_{0}}\left( q,\dot{q} \right)\dot{q}-{{G}_{0}}\left( q \right)]- \\ & \frac{d}{dt}{{{\ddot{q}}}_{d}}+\bar{F}\left( q,\dot{q},\ddot{q} \right), \\ \end{align}$ | (35) |
式中F(q,${\dot{q}}$,${\ddot{q}}$)=M0-1 (q)${\dot{\tau }}$d+M0-1 (q)${\dot{F}}$(q,${\dot{q}}$,${\ddot{q}}$)+${\dot{M}}$0-1(q)τd+${\dot{M}}$0-1(q)F(q,${\dot{q}}$,${\ddot{q}}$)。因此
| $\left\| \bar{F}\left( q,\dot{q},\ddot{q} \right) \right\| <{{{\bar{B}}}_{0}}+{{{\bar{B}}}_{1}}\left\| q \right\|+{{{\bar{B}}}_{2}}{{\left\| {\dot{q}} \right\|}^{2}}$ | (36) |
式中,B0、B1、B2是正常数。
注 2 因机械手物理结构有其制约范围,而且干扰力矩τd也是有界的,式(36)是有效的。
定义线性滑模面:
| $\sigma =\dot{e}+\beta e,$ | (37) |
式中 β=diag(β11,…,β1n)是设计矩阵。式(37)的一阶和二阶导数为
| $\left\{ \begin{matrix} \dot{\sigma }=\ddot{e}+\beta \dot{e}, \\ \ddot{\sigma }=\frac{d}{dt}\ddot{e}+\beta \ddot{e}=\frac{d}{dt}(\ddot{q}-{{{\ddot{q}}}_{d}})+\beta \ddot{e} \\ \end{matrix} \right.$ | (38) |
n关节机械手的非奇异终端滑模面选取为
| $s=\sigma +K{{{\dot{\sigma }}}^{p/q}},$ | (39) |
式中K=diag(k11,…,k1n)是设计矩阵。
对式(39)求导数:
| $\dot{s}=\dot{\sigma }+\left( p/k \right)K{{{\dot{\sigma }}}^{p/q-1}}\ddot{\sigma }=\left( p/q \right)K{{{\dot{\sigma }}}^{p/q-1}}(\ddot{\sigma }+\left( q/p \right){{K}^{-1}}{{{\dot{\sigma }}}^{2-p/q}}),$ | (40) |
为保证收敛误差为零,控制力矩设计为
| $\dot{\tau }={{{\dot{u}}}_{0}}+{{{\dot{u}}}_{1}},$ | (41) |
| $\begin{align} & {{{\dot{u}}}_{0}}={{M}_{0}}\left( q \right)\frac{d}{dt}{{{\ddot{q}}}_{d}}+\frac{d}{dt}[{{C}_{0}}\left( q,\dot{q} \right)\dot{q}+{{G}_{0}}\left( q \right)]-(\left( q/p \right){{K}^{-1}}{{M}_{0}}{{{\dot{\sigma }}}^{2-p/q}})- \\ & \beta {{M}_{0}}\ddot{e}-{{M}_{0}}{{{\dot{M}}}^{-1}}_{0}~(\tau -{{C}_{0}}\left( q,\dot{q} \right)\dot{q}-{{G}_{0}}\left( q \right)), \\ \end{align}$ | (42) |
| ${{{\dot{u}}}_{1}}=-{{K}^{*}}{{M}_{0}}\left( q \right)s-{{M}_{0}}\left( q \right)({{{\bar{B}}}_{0}}+{{{\bar{B}}}_{1}}\left\| q \right\|+{{{\bar{B}}}_{2}}{{\left\| {\dot{q}} \right\|}^{2}})sign\left( s \right),$ | (43) |
式中K*=-diag(k11*,…,k1n*),是正定矩阵。因为机械手精确数学模型难以得到,B0、B1和B2的计算较为复杂,为此,设计自适应调节律对这些值进行估计,式(43)调整为
| ${{{\dot{u}}}_{1}}=-{{K}^{*}}{{M}_{0}}\left( q \right)s-{{M}_{0}}\left( q \right)\left( {{B}_{0e}}+{{B}_{1e}}\left\| q \right\|+{{B}_{2e}}{{\left\| {\dot{q}} \right\|}^{2}} \right)sign(s)$ | (44) |
定义自适应误差 ${\tilde{\bar{B}}}$0=B0e-B0,${\tilde{\bar{B}}}$1=B1e-B1,${\tilde{\bar{B}}}$2=B2e-B2,考虑‖s‖不能在有限时间内精确为零,利用死区技术,参数B0e、B1e、B2e采用如下自适应律估计:
| ${{{\dot{B}}}_{0e}}={{\vartheta }_{1}}\left( \frac{p}{q} \right)\left\| K \right\|{{\|}^{\left( p/q \right)-1}}s\|,\|s\|\ge \zeta ;\text{ }0,\left\| s \right\|<\zeta $ | (45) |
| ${{{\dot{B}}}_{1e}}=\left\{ \begin{matrix} {{\vartheta }_{1}}\left( \frac{p}{q} \right)\left\| K \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|\left\| q \right\|, & \|s\|\ge \zeta ; \\ 0, & \left\| s \right\|<\zeta \\ \end{matrix} \right.$ | (46) |
| ${{{\dot{B}}}_{2e}}=\left\{ \begin{matrix} {{\vartheta }_{2}}\left( \frac{p}{q} \right)\left\| K \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|{{\left\| {\dot{q}} \right\|}^{2}}, & \left\| s \right\|\ge \zeta ; \\ 0, & \left\| s \right\|<\zeta \\ \end{matrix} \right.$ | (47) |
式中,调节参数$\vartheta $0、$\vartheta $1、$\vartheta $3是正数。
定义Lyapunov函数Vm分析系统稳定性:
| ${{V}_{m}}=\frac{1}{2}[{{s}^{T}}s+{{\gamma }_{0}}~{{{\tilde{\bar{B}}}}^{2}}_{0}+{{\gamma }_{1}}{{{\tilde{\bar{B}}}}^{2}}_{1}+{{\gamma }_{2}}{{{\tilde{\bar{B}}}}^{2}}_{2}],$ | (48) |
对式(48)求导,并结合式(40)可得:
| $\begin{align} & {{{\dot{V}}}_{m}}={{s}^{T}}+{{\gamma }_{0}}~\tilde{\bar{B}}{{~}_{0}}{{{\dot{B}}}_{0e}}+{{\gamma }_{1}}{{{\tilde{\bar{B}}}}_{1}}{{{\dot{B}}}_{1e}}+{{\gamma }_{2}}{{{\tilde{\bar{B}}}}_{2}}{{{\dot{B}}}_{2e}}= \\ & \left( p/k \right)K{{{\dot{\sigma }}}^{p/q-1}}{{s}^{T}}\left( \ddot{\sigma }+\left( q/p \right){{K}^{-1}}{{{\dot{\sigma }}}^{2-p/q}} \right)+ \\ & {{\gamma }_{0}}\left( {{B}_{0e}}-{{{\tilde{\bar{B}}}}_{0}} \right){{B}_{0e}}+{{\gamma }_{1}}\left( {{B}_{1e}}-{{{\tilde{\bar{B}}}}_{1}} \right){{{\dot{B}}}_{1e}}+{{\gamma }_{2}}\left( {{B}_{2e}}-{{{\tilde{\bar{B}}}}_{2}} \right){{{\dot{B}}}_{2e}} \\ \end{align}$ | (49) |
结合式(35)和式(38)得:
| $\begin{align} & {{{\dot{V}}}_{m}}=\left( p/q \right)K{{{\dot{\sigma }}}^{p/q-1}}{{s}^{T}}\left\{ M_{0}^{-1} \right.\left( q \right)\left[ \dot{\tau }-\frac{d}{dt}\left( {{C}_{0}}\left( q,\dot{q} \right)\dot{q}+{{G}_{0}}\left( q \right) \right) \right]+ \\ & \text{ }M_{0}^{-1}\left( q \right)[\tau -{{C}_{0}}\left( q,\dot{q} \right)\dot{q}-{{G}_{0}}\left( q \right)]-\frac{d}{dt}{{{\ddot{q}}}_{d}}+\left. \left( q,\dot{q},\ddot{q} \right) \right\}+ \\ & \text{ }(\left( {{B}_{0e}}-{{{\bar{B}}}_{0}} \right){{\gamma }_{0}}{{\vartheta }_{0}}\left( q/p \right)\left\| K \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|+ \\ & \text{ }(\left( {{B}_{1e}}-{{{\bar{B}}}_{1}} \right){{\gamma }_{1}}{{\vartheta }_{1}}\left( q/p \right)\left\| K \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|\left\| q \right\|+ \\ & \text{ }(\left( {{B}_{2e}}-{{{\bar{B}}}_{2}} \right){{\gamma }_{2}}{{\vartheta }_{2}}\left( q/p \right)\left\| K \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|{{\left\| {\dot{q}} \right\|}^{2}} \\ \end{align}$ | (50) |
利用式(41)、(42)和(44)得:
| $\begin{align} & {{{\dot{V}}}_{m}}\le \left( p/q \right)\left\| K \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|[\left\| \dot{F}\left( q,\dot{q},\ddot{q} \right) \right\|\left\| s \right\|-{{K}^{*}}\left\| s \right\|-\left\| \left( {{B}_{0e}}+{{B}_{1e}}\left\| q \right\|+{{B}_{2e}}{{\left\| {\dot{q}} \right\|}^{2}} \right) \right\|\left\| s \right\|+\text{ } \\ & \left\| \left( {{{\bar{B}}}_{0}}+{{{\bar{B}}}_{1}}\left\| q \right\|+{{{\bar{B}}}_{2}}{{\left\| {\dot{q}} \right\|}^{2}} \right) \right\|\left\| s \right\|-\left\| \left( {{{\bar{B}}}_{0}}+{{{\bar{B}}}_{1}}\left\| q \right\|+{{{\bar{B}}}_{2}}{{\left\| {\dot{q}} \right\|}^{2}} \right) \right\|\left\| s \right\|+ \\ & \left( \left\| {{B}_{0e}}-{{{\bar{B}}}_{0}} \right\| \right){{\gamma }_{0}}{{\vartheta }_{0}}\left\| s \right\|+\left( \left\| {{B}_{1e}}-{{{\bar{B}}}_{1}} \right\| \right){{\gamma }_{1}}{{\vartheta }_{1}}\left\| s \right\|\left\| q \right\|+\left( \left\| {{B}_{2e}}-{{{\bar{B}}}_{2}} \right\| \right){{\gamma }_{2}}{{\vartheta }_{2}}\left\| s \right\|\left. {{\left\| {\dot{q}} \right\|}^{2}} \right]\le \\ & \left( - \right.\underbrace{\left[ \left\| \left( {{{\bar{B}}}_{0}}+{{{\bar{B}}}_{1}}\left\| q \right\|{{+}_{2}}{{\left\| {\dot{q}} \right\|}^{2}} \right) \right\|-\left\| \left( q,\dot{q},\ddot{q} \right) \right\| \right]}_{{{\beta }_{\sigma 1}}}\left\| s \right\|- \\ & \left( \left\| {{B}_{0e}}-{{{\bar{B}}}_{0}} \right\| \right)\underbrace{\left[ \left\| s \right\|-{{\gamma }_{0}}{{\vartheta }_{0}}\left\| s \right\| \right]}_{{{\beta }_{\gamma 1}}}-\left( \left\| {{B}_{1e}}-{{{\bar{B}}}_{1}} \right\| \right)\underbrace{\left[ \left\| q \right\|\left\| s \right\|-{{\gamma }_{1}}{{\vartheta }_{1}}\left\| q \right\|\left\| s \right\| \right]}_{{{\beta }_{\delta 1}}}- \\ & \left( \left\| {{B}_{2e}}-{{{\bar{B}}}_{2}} \right\| \right)\underbrace{\left[ \left\| {\dot{q}} \right\|\left\| s \right\|-{{\gamma }_{2}}{{\vartheta }_{2}}{{\left\| q \right\|}^{2}}\left\| s \right\| \right]}_{{{\beta }_{\rho 1}}}\le \\ & -{{\beta }_{\sigma 1}}\sqrt{2}\frac{\left\| s \right\|}{\sqrt{2}}-{{\beta }_{\gamma 1}}\sqrt{2{{\gamma }_{0}}}\frac{~{{{\tilde{\bar{B}}}}_{0}}}{\sqrt{2{{\gamma }_{0}}}}-{{\beta }_{\delta 1}}\sqrt{2{{\gamma }_{1}}~}\frac{{{{\tilde{\bar{B}}}}_{1}}}{\sqrt{2{{\gamma }_{1}}}}-{{\beta }_{\rho 1}}\sqrt{2{{\gamma }_{2}}}\frac{~{{{\tilde{\bar{B}}}}_{2}}}{\sqrt{2{{\gamma }_{2}}}} \\ \end{align}$ | (51) |
因此,
| $\begin{align} & {{{\dot{V}}}_{m}}\le -min\left\{ \sqrt{2}{{\beta }_{\sigma 1}},\sqrt{2\gamma _{0}^{-1}}~{{\beta }_{\gamma 1}},\sqrt{2\gamma _{1}^{-1}}~{{\beta }_{\delta 1}},\sqrt{2\gamma _{2}^{-1}}~{{\beta }_{\rho 1}} \right\} \\ & \frac{\left\| s \right\|}{\sqrt{2}}+\frac{\sqrt{{{\gamma }_{0}}}}{\sqrt{2}}\left\| {{{\tilde{\bar{B}}}}_{0}} \right\|+\frac{\sqrt{{{\gamma }_{1}}}}{\sqrt{2}}\left\| {{{\tilde{\bar{B}}}}_{1}} \right\|+\frac{\sqrt{{{\gamma }_{2}}}}{\sqrt{2}}\left\| {{{\tilde{\bar{B}}}}_{2}} \right\|\le -{{\beta }_{c0}}{{V}^{1/2}}\left( t \right) \\ \end{align}$ | (52) |
式中,
图 1为二关节机械手结构示意图,所提出的自适应二阶终端滑模控制器应用于该二关节机械手的轨迹跟踪,仿真基于Matlab/simulink实现,仿真步长设置为0.004 s。

|
图 1 二关节机械手结构 Figure 1 Structrue of a two-link robotic manipulator |
针对二关节机械手动态方程,相关参数为
| $\begin{align} & M\left( q \right)=\left[ \begin{matrix} \left( {{m}_{1}}+{{m}_{2}} \right)l_{1}^{2}+{{m}_{2}}l_{2}^{2}+2{{m}_{2}}{{l}_{1}}{{l}_{2}}{{c}_{2}}+{{J}_{1}} & {{m}_{2}}l_{2}^{2}+{{m}_{2}}{{l}_{1}}{{l}_{2}}{{c}_{2}} \\ {{m}_{2}}l_{2}^{2}+{{m}_{2}}{{l}_{1}}{{l}_{2}}{{c}_{2}} & {{m}_{2}}l_{2}^{2}+{{J}_{2}} \\ \end{matrix} \right],\text{ } \\ & C\left( q,\dot{q} \right)\dot{q}=\left[ \begin{matrix} -{{m}_{2}}{{l}_{1}}{{l}_{2}}{{s}_{2}}{{{\dot{q}}}^{2}}_{2}-2{{m}_{2}}{{l}_{1}}{{l}_{2}}{{s}_{2}}{{{\dot{q}}}_{1}}{{{\dot{q}}}_{2}} \\ {{m}_{2}}{{l}_{1}}{{l}_{2}}{{s}_{2}}{{{\dot{q}}}^{2}}_{2} \\ \end{matrix} \right], \\ \end{align}$ |
令x1(t)=q1(t),x2(t)=1(t),x3(t)=q2(t),x4(t)=${\dot{q}}$2(t),二关节机械手的物理参数分别为l1=1 m,l2=0.85 m,J1=5 kg·m,J2=5 kg·m,m1=0.5 kg,m2=1.5 kg,关节的标称质量1=0.4 kg,2=1.2 kg,g=9.81 m/s2。 参考信号qd1=sin(t),qd2=sin(t),初始状态为:q1(0)=0.5,q2(0)=-0.5,${\dot{q}}$1(0)=0,${\dot{q}}$2(0)=0,外部干扰看作为:τd1=1.5sin(t)+0.5cos(100πt),τd2=sin(2t)+0.5cos(100πt),r=0,控制器参数设计为p=5,q=3,K=diag(0.023,0.023),β=diag(45,45),ε=0.005,K*=diag(60,60),自适应律设计为
| $\begin{align} & {{{\dot{B}}}_{0e}}=\left\{ \begin{matrix} 1.74\left\| K \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|, & \left\| s \right\|\ge 0.000\text{ }5, \\ 0, & \left\| s \right\| <0.000\text{ }5 \\ \end{matrix} \right.~ \\ & {{{\dot{B}}}_{1e}}=\left\{ \begin{matrix} 1.45\left\| K \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|\left\| q \right\|, & \left\| s \right\|\ge 0.000\text{ }5; \\ 0, & \left\| s \right\|<0.000\text{ }5 \\ \end{matrix} \right.~ \\ & {{{\dot{B}}}_{2e}}=\left\{ \begin{matrix} 3.30\left\| K \right\|\left\| {{{\dot{\sigma }}}^{\left( p/q \right)-1}}s \right\|{{\left\| {\dot{q}} \right\|}^{2}}, & \left\| s \right\|\ge 0.000\text{ }5; \\ 0, & \left\| s \right\|<0.000\text{ }5 \\ \end{matrix} \right. \\ \end{align}$ |
初始值取B0e(0)=1,B1e(0)=1,B2e(0)=1。
为对比控制性能,亦对文献[21]非奇异终端滑模控制方法进行仿真,控制器设计为
| $\left\{ \begin{matrix} {{\tau }_{f}}={{C}_{0}}\left( q,\dot{q} \right)\dot{q}+{{G}_{0}}\left( q \right)+{{M}_{0}}\left( q \right){{{\ddot{q}}}_{d}}+{{u}_{a}}+{{u}_{b}},~ \\ {{u}_{a}}=-\frac{q}{p}{{M}_{0}}\left( q \right){{K}^{-1}}{{{\dot{e}}}^{2-p/q}}, \\ {{u}_{b}}=-\frac{p{{\left[ {{s}^{T}}Kdiag\left( {{{\dot{e}}}^{p/q-1}}M_{0}^{-1}\left( q \right) \right) \right]}^{T}}}{q\left\| {{s}^{T}}Kdiag\left( {{{\dot{e}}}^{p/q-1}}M_{0}^{-1}\left( q \right) \right) \right\|}\left[ \left\| s \right\|\left\| Kdiag\left( {{{\dot{e}}}^{p/q-1}} \right)M_{0}^{-1}\left( q \right) \right\|\left( {{\rho }_{0}}+{{\rho }_{1}}\left\| {\dot{q}} \right\|+{{\rho }_{2}}{{\left\| {\dot{q}} \right\|}^{2}} \right) \right] \\ \end{matrix} \right.$ | (53) |
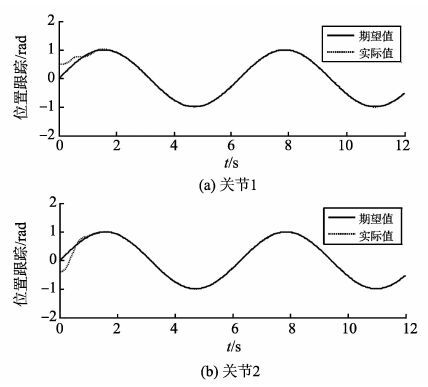
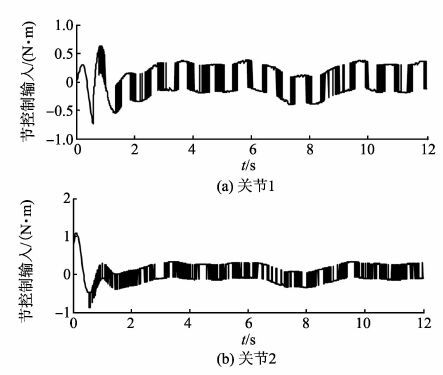
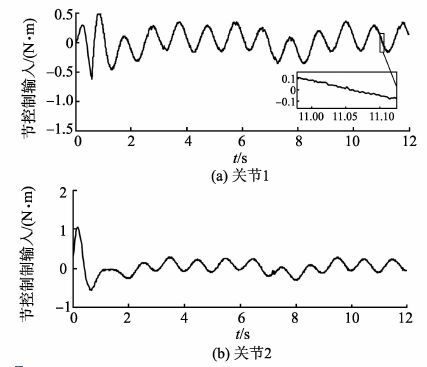
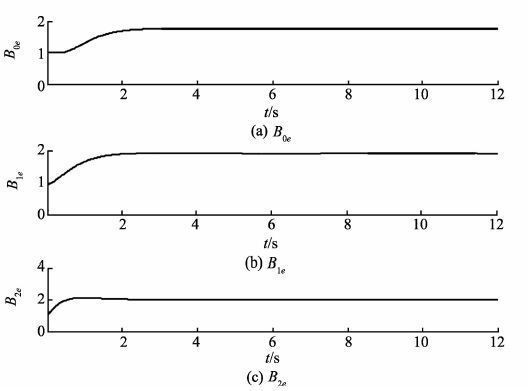
两种控制器作用下,跟踪响应和控制输入分别如图 2~5所示,通过观察分析可得,两种方法作用下都有良好的跟踪性能,但如图 4所示,非奇异终端滑模控制方法下控制抖振严重,关节1、关节2的控制输入在抖振幅值约为±0.5的范围内高频振荡,极易引起执行结构损坏,而在本研究所提出方法下,控制输入作用连续,如图 5所示,抖振现象大大减少,控制作用连续、平滑,而且,本研究所提方法不需要已知不确定性上界,参数B0e,B1e,B2e估计值如图 6所示。
|
图 2 本研究所提算法下机械手轨迹跟踪 Figure 2 Trajectory tracking response of robotic manipulator under the proposed algorithm |

|
图 3 文献[21]所提算法下机械手轨迹跟踪 Figure 3 Trajectory tracking response of robotic manipulator under the controller in [21] |
|
图 4 所提算法下控制输入 Figure 4 Control input under the controller in [21] |
|
图 5 本研究所提算法下控制输入 Figure 5 Control input under the proposed algorithm |
|
图 6 本研究所提算法下参数估计值 Figure 6 Estimated parameters under the proposed algorithm |
本研究针对具有不确定性的机械手操作系统提出一种自适应终端滑模控制方案。首先针对一类MIMO非线性不确定系统设计了自适应终端滑模控制器,不连续控制包含在控制输入的微分项,使得实际控制作用连续,设计自适应律克服系统不确定性上界未知问题,然后针对机械手系统设计自适应终端滑模轨迹跟踪控制器,最后针对二关节机械手的仿真结果验证了所提出算法的有效性,并且与一种非奇异终端滑模控制方法进行对比研究,表明所提控制方案在削弱控制抖振、不需要已知不确定上界方面的优越性,实现了机械手轨迹的高精度跟踪。
| [1] | GALICKI M. Finite-time control of robotic manipulators[J]. Automatica , 2015, 51 : 49-54 DOI:10.1016/j.automatica.2014.10.089 |
| [2] | VERRELLI C M, PIROZZI S, TOMEI P, et al. Linear repetitive learning controls for robotic manipulators by padé approximants[J]. IEEE Transactions on Control Systems Technology , 2015, 23 (5) : 2063-2070 DOI:10.1109/TCST.2015.2396012 |
| [3] |
孟健, 李贻斌, 李彬. 四足机器人跳跃步态控制方法[J].
山东大学学报(工学版) , 2015, 45 (3) : 28-34 MENG Jian, LI Yibin, LI Bin. Bound gait controlling method of quadruped robot[J]. Journal of School of Shandong University (Engineering Science) , 2015, 45 (3) : 28-34 |
| [4] | PARK C W. Robust stable fuzzy control via fuzzy modeling and feedback linearization with its applications to controlling uncertain single-link flexible joint manipulators[J]. Journal of Intelligent and Robotic Systems , 2004, 39 (2) : 131-147 DOI:10.1023/B:JINT.0000015344.84152.dd |
| [5] | NIKDEL N, NIKDEL P, BADAMCHIZADEH M A, et al. Using neural network model predictive control for controlling shape memory alloy-based manipulator[J]. IEEE Transactions on Industrial Electronics , 2014, 61 (3) : 1394-1401 DOI:10.1109/TIE.2013.2258292 |
| [6] | LI Z, YANG C, SU C Y, et al. Decentralized fuzzy control of multiple cooperating robotic manipulators with impedance interaction[J]. IEEE Transactions on Fuzzy Systems , 2015, 23 (4) : 1044-1056 DOI:10.1109/TFUZZ.2014.2337932 |
| [7] | LI Z, DENG S, SU C Y, et al. Decentralized adaptive control of cooperating robotic manipulators with disturbance observers[J]. IET Control Theory & Applications , 2014, 8 (7) : 515-521 |
| [8] |
翟伟娜, 葛运旺, 宋书中. 基于改进趋近律的机械手滑模控制[J].
信息与控制 , 2014, 43 (3) : 300-305 ZHAI Weina, GE Yunwang, SONG Shuzhong. Sliding mode control for robotic manipulators based on the improved reaching Law[J]. Information and Control , 2014, 43 (3) : 300-305 |
| [9] | LI F, WU L, SHI P, et al. State estimation and sliding mode control for semi-Markovian jump systems with mismatched uncertainties[J]. Automatica , 2015, 51 : 385-393 DOI:10.1016/j.automatica.2014.10.065 |
| [10] |
刘向杰, 韩耀振. 基于连续高阶模滑的多机电力系统励磁控制[J].
山东大学学报 (工学版) , 2016, 46 (2) : 64-71 LIU Xiangjie, HAN Yaozhen. Multi-machine power system excitation control based on continuous higher-order sliding mode[J]. Journal of School of Shandong University (Engineering Science) , 2016, 46 (2) : 64-71 |
| [11] | HAN Y, LIU X. Continuous higher-order sliding mode control with time-varying gain for a class of uncertain nonlinear systems[J]. ISA Transactions , 2016, 62 : 193-201 DOI:10.1016/j.isatra.2016.02.005 |
| [12] | LIU X, HAN Y. Decentralized multi-machine power system excitation control using continuous higher-order sliding mode technique[J]. International Journal of Electrical Power & Energy Systems , 2016, 82 : 76-86 |
| [13] | YANG J, SU J, LI S, et al. High-order mismatched disturbance compensation for motion control systems via a continuous dynamic sliding-mode approach[J]. IEEE Transactions on Industrial Informatics , 2014, 10 (1) : 604-614 DOI:10.1109/TII.2013.2279232 |
| [14] |
张德江, 张袅娜, 冯勇. 参数不确定柔性机械手的快速终端滑模控制[J].
控制与决策 , 2010, 25 (3) : 433-436 ZHANG Dejiang, ZHANG Niaona, FENG Yong. Fast terminal sliding mode control for flexible manipulators with uncertain parameters[J]. Control and Decision , 2010, 25 (3) : 433-436 |
| [15] | JIN M, LEE J, CHANG P H, et al. Practical nonsingular terminal sliding-mode control of robot manipulators for high-accuracy tracking control[J]. IEEE Transactions on Industrial Electronics , 2009, 56 (9) : 3593-3601 DOI:10.1109/TIE.2009.2024097 |
| [16] | WANG L, CHAI T, ZHAI L. Neural-network-based terminal sliding-mode control of robotic manipulators including actuator dynamics[J]. IEEE Transactions on Industrial Electronics , 2009, 56 (9) : 3296-3304 DOI:10.1109/TIE.2008.2011350 |
| [17] | FENG Y, YU X, MAN Z. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica , 2002, 38 (12) : 2159-2167 DOI:10.1016/S0005-1098(02)00147-4 |
| [18] | MONDAL S, MAHANTA C. Adaptive integral higher order sliding mode controller for uncertain systems[J]. Journal of Control Theory and Applications , 2013, 11 (1) : 61-68 DOI:10.1007/s11768-013-1180-5 |
| [19] | PLESTAN F, SHTESSEL Y, BREGEAULT V, et al. New methodologies for adaptive sliding mode control[J]. International Journal of Control , 2010, 83 (9) : 1907-1919 DOI:10.1080/00207179.2010.501385 |
| [20] | MOHAMMADI A, TAVAKOLI M, MARQUEZ H J, et al. Nonlinear disturbance observer design for robotic manipulators[J]. Control Engineering Practice , 2013, 21 (3) : 253-267 DOI:10.1016/j.conengprac.2012.10.008 |
| [21] | ZHAO D, ZHU Q, LI N, et al. Synchronized control with neuro-agents for leader—follower based multiple robotic manipulators[J]. Neurocomputing , 2014, 124 : 149-161 DOI:10.1016/j.neucom.2013.07.016 |
| [22] | LIU H, ZHANG T. Neural network-based robust finite-time control for robotic manipulators considering actuator dynamics[J]. Robotics and Computer-Integrated Manufacturing , 2013, 29 (2) : 301-308 DOI:10.1016/j.rcim.2012.09.002 |



