面对海量数据,推荐系统能够挑选用户潜在感兴趣的商品并提供个性化推荐服务,成为电子商务、网络搜索、音乐/视频点播等Web 2.0服务的核心技术[1-3]。协同过滤是推荐系统中一种成功的推荐技术,其基本思想是依据用户过去的评分记录、购买记录以及评论等信息,搜寻与目标用户有类似兴趣爱好的用户作为近邻,那么目标用户很有可能喜欢其近邻喜欢的内容。因此搜集到的用户信息越丰富,推荐的内容越能够满足用户的需求。然而协同过滤受到数据稀疏性问题的制约,导致系统的推荐质量低下[1-3]。
数据稀疏性是指在推荐过程中可用的数据稀少,使得系统难以搜寻到目标用户真正的近邻。为了降低数据稀疏性对推荐结果的影响,传统的协同过滤方法常常采用余弦相似性(Cosine,COS)[4]和相关相似性(Pearson correlation coefficient,PCC)[5]2种相似性度量方法搜寻目标用户的近邻。然而COS和PCC方法仅仅利用了两两用户共同评分项上的少量评分计算用户之间的相似度,故而无法保证目标用户近邻的准确性和可靠性。针对上述问题,许多研究人员提出了改进的推荐算法以提高系统在评分数据极端稀疏环境下的性能。文献[6]首先利用联合聚类方法将原始的用户—项目评分矩阵划分为多个子评分矩阵,然后利用加权非负矩阵分解方法在各个子评分矩阵上预测未评分项;文献[7]借鉴多渠道扩散相似性模型,提出一种融合扩散过程和用户评分奇异性的推荐算法;文献[8]提出一种基于用户群体影响的算法。该算法在计算两两用户的相似度时,不仅考虑了用户之间的相似性,同时还考虑了用户所处群体之间的相似性;文献[9]提出了一种修正的推荐算法。该算法同时考虑了用户评分倾向、共同评分项、相似性度量方法等因素以获取目标用户准确可靠的近邻;文献[10]增加考虑了用户的评分尺度,提出一种改进的COS相似性度量方法(Adjusted COS,ACOS);文献[11]进一步考虑了用户之间信息熵的差异和相似性,基于0-1背包问题的求解策略提出了一种优化的近邻选择算法;文献[12]利用sigmoid函数提出一种改进的PCC方法(Sigmoid based PCC,SPCC)。该方法考虑了两两用户共同评分项数量这一因素对相似度的影响。文献[13]依据用户不同的评分偏好将所有用户逐一划分到不同的用户群体,提出了一种基于用户偏好聚类的推荐算法。
虽然研究人员提出了大量有效的算法来改善推荐系统的性能[14-16],然而由于评分数据极端稀疏,因此充分利用搜集的评分信息是提高预测质量和推荐性能的关键。尽管有的研究人员提出采用数据填补技术降低评分数据的稀疏性,但填补手段仍然会受到数据稀疏性的制约。基于此,本研究提出了一种基于模糊信息熵的相似性度量方法。首先定义了用户的模糊信息熵衡量用户评分偏好的不确定程度;其次,从全局考虑两两用户评分偏好的关联,利用模糊互信息衡量两两用户评分偏好的相似程度;最后,同时考虑用户之间的模糊互信息和模糊信息熵之差,设计了一种新的相似性度量方法。该方法联合用户的模糊信息熵以及两两用户的模糊互信息,充分利用用户所有的评分信息来刻画用户之间的相似性。试验结果表明:所提算法能够改善系统对稀疏数据的处理能力,在数据稀疏情况下能够有效提高协同过滤的预测质量和推荐性能。
1 预备知识 1.1 协同过滤推荐方法在推荐系统中,用户的评分数据可在一个m×n的评分矩阵中表示。其中,用户评分矩阵包含m个用户和n个项目,rui表示用户u在项目i上的评分。若用户u在项目i上的评分未知,rui记为0。对于目标用户,算法需要获取其近邻集合以计算目标项的评分。而近邻的选取取决于用户间的相似度,与目标用户相似度较大的前k个用户组成近邻集合。常用的相似性度量方法主要有COS和PCC 2种,计算公式分别为:
| $sim{{\left( a,b \right)}^{COS}}=\frac{\sum\limits_{i\in {{I}_{ab}}}{~{{r}_{ai}}}\times {{r}_{bi}}}{\sqrt{\sum\limits_{i\in {{I}_{ab}}}{r_{ai}^{2}}}\times \sqrt{\sum\limits_{i\in {{I}_{ab}}}{r_{bi}^{2}}}},$ | (1) |
| $sim{{\left( a,b \right)}^{PCC}}=\frac{\sum\limits_{i\in {{I}_{ab}}}{({{r}_{ai}}-\overline{{{r}_{a}}})}\times ({{r}_{bi}}-\overline{{{r}_{b}}})}{\sum\limits_{i\in {{I}_{ab}}}{{{({{r}_{ai}}-\overline{{{r}_{a}}})}^{2}}}\times \sum\limits_{i\in {{I}_{ab}}}{{{({{r}_{bi}}-\overline{{{r}_{b}}})}^{2}}}}$ | (2) |
式中,sim(a,b)表示用户a和用户b的相似性; Iab表示a和b的共同评分项集合; rai表示a在项目i上的评分; ra和rb分别表示a和b在Iab上的平均评分。
计算得到两两用户的相似性以后,根据相似性大小获取目标用户的近邻。最后产生推荐结果[11]:
| ${{P}_{ti}}=\overline{{{r}_{t}}}+\frac{\sum\limits_{g=1}^{k}{sim}\left( t,g \right)\times ({{r}_{gi}}-\overline{{{r}_{g}}})}{\sum\limits_{g=1}^{k}{\left| sim\left( t,g \right) \right|}},$ | (3) |
式中,Pti表示目标用户t在未评分项i上的预测结果;rgi表示用户g在项目i上的评分; rt和rg分别表示t和g在所有项目上的平均评分;k为近邻数。 另外,由于推荐系统面临着严峻的数据稀疏性问题,故搜寻到的近邻无法保证在目标项具有评分。 若目标用户的近邻对目标项都没有评分,则算法无法计算目标用户在该目标项上的预测结果。
1.2 模糊信息理论模糊信息理论由信息理论扩展且更具普遍性。
定义 1 假设A={a1,a2,…,am} ( m≥2)是一个有限的样本集合,F是样本的属性集合,则集合A在属性空间F下的关系矩阵
| ${{M}_{F}}=\left[ \begin{matrix} {{f}_{11}} & {{f}_{12}} & \cdots & {{f}_{1m}} \\ {{f}_{21}} & {{f}_{22}} & \cdots & {{f}_{2m}} \\ \vdots & \vdots & \ddots & \vdots \\ {{f}_{m1}} & {{f}_{m2}} & \cdots & {{f}_{mm}} \\ \end{matrix} \right]~,$ | (4) |
其中,fij表示样本ai和样本aj在属性空间F下的模糊等价关系。 模糊等价关系可以通过计算ai和aj在属性空间F下的相似性得到,fij∈[0,1]。
定义 2 在关系矩阵MF下,属性集合F的模糊信息熵
| $~FH({{M}_{F}})=-\frac{1}{m}\sum\limits_{i=1}^{m}{log}\frac{\left\| {{\left[ {{a}_{i}} \right]}_{F}} \right\|}{m},$ | (5) |
其中,FH(MF)为属性集合F的模糊信息熵;
定义 3 假设F1和F2为属性集合F的2个子集,那么F1和F2的模糊联合信息熵
| $FH({{M}_{{{F}_{1}}}},{{M}_{{{F}_{2}}}})=-\frac{1}{m}\sum\limits_{i=1}^{m}{log}\frac{\left\| {{[{{a}_{i}}]}_{{{F}_{1}}}}\cap {{[{{a}_{i}}]}_{{{F}_{2}}}} \right\|}{m}$ | (6) |
由属性子集F1和F2的模糊信息熵与F1和F2之间的模糊联合信息熵,可以计算F1和F2之间的模糊互信息
| $FMI(M{{F}_{1}},{{M}_{{{F}_{2}}}})=\text{ }FH\left( {{M}_{{{F}_{1}}}} \right)+FH\left( {{M}_{{{F}_{2}}}} \right)-FH({{M}_{{{F}_{1}}}},{{M}_{{{F}_{2}}}})$ | (7) |
传统的协同过滤方法本质上是搜寻与目标用户有相似评分偏好的用户作为其近邻,然后利用近邻记录的评分信息预测目标用户的未知属性。 然而,传统相似性度量方法只考虑了两两用户共同评分项的少量评分,因此有较大相似度的2个用户并不一定有相同的评分偏好,从而导致推荐结果存在较大的偶然性。 针对上述问题,本研究从全局上充分利用收集到的用户评分信息,提出一种基于模糊信息熵的相似性度量方法。 所提方法一方面利用模糊信息熵衡量用户偏好的不确定程度,另外,利用模糊互信息获取两两用户评分偏好的关联程度,使得搜寻到的近邻更加准确合理。
2.1 单个用户的模糊信息熵在推荐系统中,用户对商品的评分能够反映该用户的评分偏好。 例如,有些用户对商品要求严苛,以致对商品给出的评分普遍偏低,而有些用户则倾向给高分。 基于此,结合用户所有的评分信息,提出一种基于模糊信息熵的度量方法以判断用户偏好的不确定性。
定义 4 假设U为用户集合,用户u∈U,项目集合记为I={i1,i2,…,in}(n≥2)。则在项目集合I上关于用户u的关系矩阵
| ${{M}_{u}}=\left( \begin{matrix} {{s}_{11}} & {{s}_{12}} & \cdots & {{s}_{1n}} \\ {{s}_{21}} & {{s}_{22}} & \cdots & {{s}_{2n}}~ \\ \vdots & \vdots & \ddots & \vdots \\ {{s}_{n1}} & {{s}_{n2}} & \cdots & {{s}_{nn}} \\ \end{matrix} \right),$ | (8) |
其中,sxy表示项目ix(1≤x≤n)和项目iy(1≤y≤n)关于用户u的模糊等价关系,其取值范围为[0,1]。模糊等价关系的计算公式定义为
| ${{s}_{xy}}=\left\{ \begin{matrix} exp\left( -\frac{1}{2}\times |{{r}_{ux}}-{{r}_{uy}}| \right), & {{r}_{ux}}-{{r}_{uy}}<{{r}_{med}}; \\ 0, & otherwise \\ \end{matrix} \right.$ | (9) |
定义4中,通过充分利用用户的评分,以获取用户的评分偏好信息。若用户u在项目ix和iy上的评分之差不小于评分中值rmed,表示单独考察用户u在项目ix和iy上的评分对于判断用户u的偏好没有帮助。 因而,在关系矩阵Mu中sxy=0;若用户u在项目ix和iy上的评分之差小于rmed,可以得知:项目ix和iy的评分在一定程度上反映了用户u的评分偏好。 特别地,如果用户u在项目ix和iy上的评分均为5分,那么关系矩阵Mu中sxy=1。
在生成关系矩阵Mu以后,依据矩阵Mu中的模糊等价关系,计算用户u的模糊信息熵。
定义 5 给定用户u的关系矩阵为Mu,可以计算用户u的模糊信息熵,计算公式为
| $FH({{M}_{u}})=-\frac{1}{n}\sum\limits_{x=1}^{n}{log}\frac{\left\| {{\left[ {{i}_{x}} \right]}_{u}} \right\|}{n},$ | (10) |
其中,FH(Mu)为用户u的模糊信息熵,‖[ix]u‖=
定义5中,依据存储在关系矩阵中的用户偏好信息,可以利用模糊信息熵有效地度量用户偏好的不确定程度。 用户之间的模糊信息熵越相近,则这两个用户很可能有相同的评分偏好,从而用户之间的相似度也越大;反之,这两个用户不可能互为近邻。
例 1 给定两个用户a和b,用户a在5个项目上的评分集合为{3,0,2,1,2},用户b在相同5个项目上的评分集合为{4,2,0,1,5},rmed=3,则用户a和b的关系矩阵
| ${M_a} = \left( {\matrix{ 1 & 0 & {0.6065} & {0.3679} & {0.6065} \cr 0 & 1 & 0 & 0 & 0 \cr {0.6065} & 0 & 1 & {0.6065} & 1 \cr {0.3679} & 0 & {0.6065} & 1 & {0.6065} \cr {0.6065} & 0 & 1 & {0.6065} & 1 \cr } } \right),$ | (11) |
| ${M_b} = \left( {\matrix{ 1 & {0.3679} & 0 & 0 & {0.6065} \cr {0.3679} & 1 & 0 & {0.6065} & 0 \cr 0 & 0 & 1 & 0 & 0 \cr 0 & {0.6065} & 0 & 1 & 0 \cr {0.6065} & 0 & 0 & 0 & 1 \cr } } \right)$ | (12) |
从而,可以计算用户a和用户b的模糊信息熵分别为:
| $FH({{M}_{a}})=-\frac{1}{5}\left( log\frac{2.639\text{ }4}{5}+log\frac{1}{5}+log\frac{2.213}{5}+log\frac{1.580\text{ }9}{5}+log\frac{3.213}{5} \right)=1.343\text{ }8,$ | (13) |
| $FH({{M}_{b}})=-\frac{1}{5}\left( log\frac{1.974\text{ }4}{5}+log\frac{1.974\text{ }4}{5}+log\frac{1}{5}+log\frac{1.606\text{ }5}{5}+log\frac{1.606\text{ }5}{5} \right)=1.655\text{ }8$ | (14) |
根据单个用户的所有评分信息,利用用户模糊信息熵度量用户评分偏好的不确定性。 在此基础上,考虑两两用户评分偏好的关联,提出一种基于模糊互信息的度量方法以反映用户之间的相似程度。
定义 6 若a和b为用户集合U中的2个用户,a和b的关系矩阵分别用Ma和Mb表示,则得到a和b的模糊联合信息熵
| $FH({{M}_{a}},{{M}_{b}})=-\frac{1}{n}\sum\limits_{x=1}^{n}{log}\frac{\left\| {{\left[ {{i}_{x}} \right]}_{a}}\cap {{\left[ {{i}_{x}} \right]}_{b}} \right\|}{n},$ | (15) |
其中:||[ix]a∩[ix]b||表示首先对Ma和Mb中第x行中的元素对应取小,然后求和。 以例1中的Ma和Mb为例,假设x=1,那么[ix]a∩[ix]b=(1,0,0,0,0.606 5),从而可以得出||[ix]a∩[ix]b||=1.606 5。依据用户a和用户b的模糊信息熵和模糊联合信息熵,可以得到用户a和用户b的模糊互信息
| $FMI({{M}_{a}},{{M}_{b}})=FH({{M}_{a}})+FH({{M}_{b}})-FH({{M}_{a}},{{M}_{b}})$ | (16) |
模糊互信息反映两两用户评分偏好的相似程度。 若a与b具有相同的评分偏好,存在FH(Ma,Mb)=FH(Ma)=FH(Mb),此时FMI(Ma,Mb)取得最大值;反之,若b与a关于评分偏好的相关性不大,则FMI(Ma,Mb)的取值相对较小,a与b互为近邻的可能性降低。
例 2 (续例1) 依据例1中用户a和b的关系矩阵,可以得到
| $${M_a} \cap {M_b} = \left( {\matrix{ 1 & 0 & 0 & 0 & {0.6065} \cr 0 & 1 & 0 & 0 & 0 \cr 0 & 0 & 1 & 0 & 0 \cr 0 & 0 & 0 & 1 & 0 \cr {0.6065} & 0 & 0 & 0 & 1 \cr } } \right),$$ | (17) |
由式(17)可计算用户a和b的模糊联合信息熵为
| $FMI({{M}_{a}},{{M}_{b}})=-\frac{1}{5}\left( log\frac{1.606\text{ }5}{5}+log\frac{1}{5}+log\frac{1}{5}+log\frac{1}{5}+log\frac{1.606\text{ }5}{5} \right)=2.048\text{ }4$ | (18) |
最后,联合a和b的模糊信息熵以及a和b的模糊联合信息熵,计算这2个用户的模糊互信息
| $FMI({{M}_{a}},{{M}_{b}})=FH({{M}_{a}})+FH({{M}_{b}})-FH({{M}_{a}},{{M}_{b}})=0.951\text{ }2$ | (19) |
推荐算法的设计主要包含2个步骤。
步骤 1 根据第2.1和2.2节的分析,设计一种基于模糊信息熵的相似性度量方法,以实现基于模糊信息熵的协同过滤算法(fuzzy information entropy based collaborative filtering,FIE-CF)。 首先对用户之间的模糊互信息进行归一化处理。 由于模糊互信息具有对称的性质,可使用以下公式代替模糊互信息参与计算用户间的相似性
| $SU({{M}_{a}},{{M}_{b}})=\frac{2FMI({{M}_{a}},{{M}_{b}})}{FH({{M}_{a}})+FH({{M}_{b}})}$ | (20) |
其中,SU(Ma,Mb)∈[0,1]。 SU(a,b)越大,用户a和用户b的相似程度越高;反之,a和b相似程度越低。
同时考虑到用户之间模糊信息熵的差异,得到a和b的相似度
| $sim{{\left( a,b \right)}^{FIE}}=\frac{2FMI({{M}_{a}},{{M}_{b}})\times exp(-|FH({{M}_{a}})-FH({{M}_{b}})|)}{FH({{M}_{a}})+FH({{M}_{b}})},$ | (21) |
式中sim(a,b)FIE∈[0,1] 。
步骤 2 预测目标用户未评分项。预测公式为
| ${{P}_{ti}}=\overline{{{r}_{t}}}+\frac{\sum\limits_{g=1}^{k}{si{{m}^{FIE}}}\left( t,g \right)\times ({{r}_{gi}}-\overline{{{r}_{g}}})}{\sum\limits_{g=1}^{k}{|si{{m}^{FIE}}\left( t,g \right)|}},$ | (22) |
其中:Pti表示目标用户t在未评分项i上的预测结果;sim(t,g)FIE表示t和g的相似性大小; rgi表示g在项目i上的评分;rg和rt分别表示g和t在所有项目上的平均评分;k为近邻数。
时间复杂度:本研究提出了一种新的相似性度量方法计算用户之间的相似性。 其中,用户模糊信息熵的计算复杂度为O(r1m),m为用户个数,r1为常数。 另外,用户之间模糊信息熵的计算复杂度为O(r2m2),r2为常数。 因此所提出的相似性度量方法的时间复杂度为O(m2)。基于上述分析,可以得出结论:相比传统的协同过滤算法(O(m2)),所提算法的时间复杂度并未提高。
3 试验结果及分析 3.1 数据集选择公开的MovieLens数据集(ML数据集)和HetRec2011-MovieLens数据集(HRML数据集)以验证算法的有效性(数据集可通过http://www.grouplens.org/下载)。 其中,ML数据集中的电影评价数据由明尼苏达大学GroupLens小组搜集得到,包含了943个用户对1 682部电影的100 000个评分数据。 由于HRML数据集中的评分数据过于稠密,故而本研究随机抽取其中1 036个用户对1 300部电影的评分,评分总数为106 210。数据集的详细描述见表 1。
| 表 1 数据集的描述 Table 1 The description of data sets |
另外,试验采用5折交叉验证法。 数据集划分为测试集和训练集,测试集占数据集的20%,余下80%数据作为训练集。测试集之间是互斥的,并有效覆盖整个数据集。
3.2 评价指标[3]试验采用平均绝对误差(mean absolute error,MAE)和覆盖率(coverage)评价所提算法的预测质量,采用推荐精度(precision)和召回率(recall)评价所提算法的推荐性能。
MAE通过计算预测评分和对应实际评分之间的偏差来评价预测结果的准确性。 MAE越小,算法预测质量越好。 Coverage通过计算获得预测评分的项目占所有项目的比例以评价预测结果的全面性。 Coverage越大,预测质量越好。
给定n个项目,有预测结果的项目有h个,算法预测的评分集合为{p1,p2,…,pn},对应实际评分集合为{r1,r2,…,rn},则MAE和Coverage的计算公式分别为:
| $MAE=\frac{\sum\limits_{i=1}^{n}{\left| {{p}_{i}}-{{r}_{i}} \right|}}{n},$ | (23) |
| $Coverage=\frac{h}{n}$ | (24) |
另外,定义推荐精度和召回率来评价系统的推荐性能。推荐精度和召回率越大推荐性能越好。 假设参与预测的用户集合为U,θ为常数(其值一般为评分中值rmed,这里设θ=rmed-0.001),|Tu|是测试集中用户u实际评分大于θ的项目数,Zu是N个项目的集合,u对这N个项目具有较大预测值。 那么,推荐精度和召回率的计算公式分别为:
| $Precision=\frac{1}{\left| U \right|}\sum\limits_{u\in U}{\frac{|\left\{ i\in {{Z}_{u}} \right.|{{r}_{ui}}>\theta \cap {{p}_{ui}}>\left. \theta \right\}|}{N}},$ | (25) |
| $Recall=\frac{1}{\left| U \right|}\sum\limits_{u\in U}{\frac{|\left\{ i\in {{Z}_{u}} \right.|{{r}_{ui}}>\theta \cap {{p}_{ui}}>\left. \theta \right\}|}{\left| {{T}_{u}} \right|}}$ | (26) |
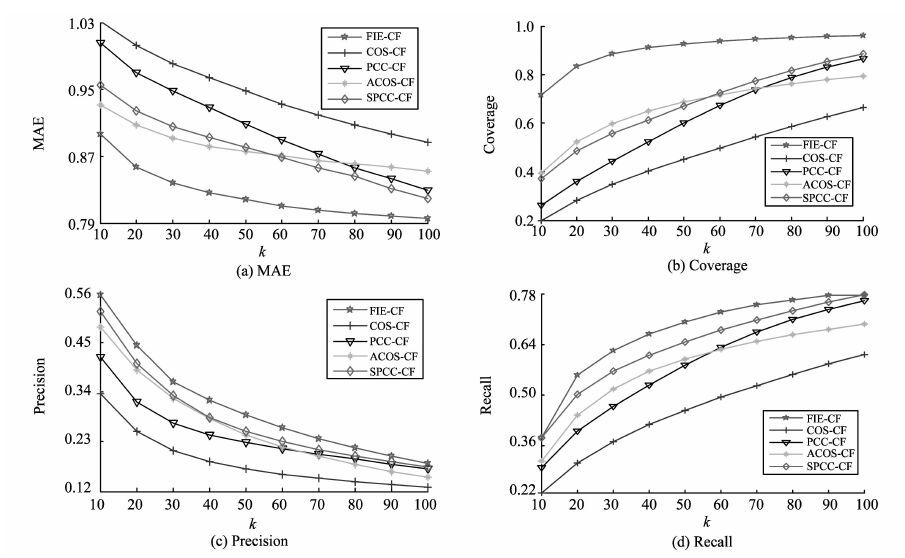
为了测试所提相似性度量方法的有效性,本研究选择4种推荐算法作为比较对象,分别为基于COS的协同过滤算法(COS-CF)[4]、基于PCC的协同过滤算法(PCC-CF)[5]、基于ACOS的协同过滤算法(ACOS-CF)[10]以及基于SPCC的协同过滤算法(SPCC-CF)[12]。 近邻数在10到100之间以步长为10变化。 试验结果见图 1与图 2。
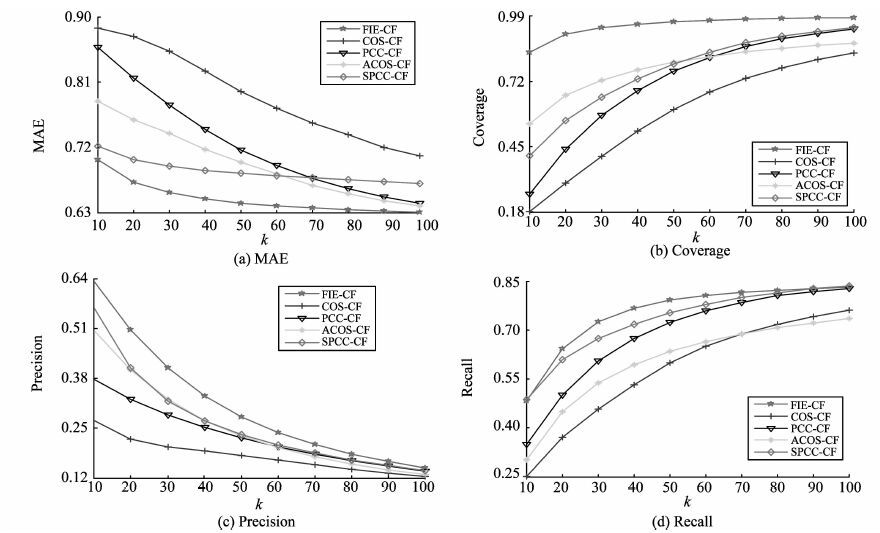
图 1分别展示了ML数据集上不同算法在4个评价指标上的变化情况。 其中,MAE的变化情况如图 1(a)所示,随着近邻数的增加,所有算法的MAE都呈现下降趋势。 而所提算法FIE-CF在整个过程都有最低的MAE值。 图 1(b)反映了算法预测的覆盖率,FIE-CF在近邻数较少时便达到70%以上,优于其他算法。 基于此,可以得出结论:相比其他4种算法,所提出的算法在ML数据集上有较高的预测质量。 另外,推荐精度和召回率的变化情况分别如图 1(c)和图 1(d)所示。 其中,项目的初始推荐数与最小近邻数相同,并与近邻数以步长10同时变化。 在推荐精度以及召回率这2个评价指标上,FIE-CF均有更优的结果,证实了所提算法在ML数据集上有较高的推荐性能。 图 2给出了HRML数据集上不同算法在4个指标上的变化情况。 试验结果显示:与ML数据集得到的结果类似,FIE-CF在HRML数据集上各项评价指标都优于其他算法。 据此,可以得出结论:所提出的相似性度量方法能有效地降低数据稀疏性对推荐结果的影响,并且所提出的推荐算法FIE-CF能显著地提高推荐结果的预测质量和推荐性能。
|
图 1 基于ML数据集的比较 Figure 1 The comparison based on ML data set |
|
图 2 基于HRML数据集的比较 Figure 2 The comparison based on HRML data set |
本研究通过充分利用评分矩阵中的用户信息,结合用户之间模糊信息熵的差异和模糊互信息,提出了一种新的相似性度量方法。 试验结果表明,所提出的算法能有效地降低数据稀疏性对推荐结果的影响,提高了推荐系统的性能。 今后的研究将继续围绕模糊信息理论展开。 如何改进模糊信息熵的计算方式来更好地刻画推荐系统中的用户行为,是提高系统性能一个可行的方向。 另外,推荐实时性也是推荐系统的一个重要评价指标,如何在保证系统性能的前提下提高推荐速度,也将是研究方向之一。
| [1] | ADOMAVICIUS G, TUZHILIN A. Toward the next generation of recommender systems: a survey of the state-of-the-art and possible extensions[J]. IEEE Transactions on Knowledge and Data Engineering , 2005, 17 (6) : 734-749 DOI:10.1109/TKDE.2005.99 |
| [2] | PAPAGELIS M, PLEXOUSAKIS D, KUTSURAS T. Alleviating the sparsity problem of collaborative filtering using trust inferences[C]//Proc of the 3rd International Conference on Trust Management. Berlin, Germany: Springer, 2005:224-239. http://cn.bing.com/academic/profile?id=1589148151&encoded=0&v=paper_preview&mkt=zh-cn |
| [3] | SHI Yue, LARSON M, HANJALIC A. Collaborative filtering beyond the user-item matrix: a survey of the state of the art and future challenges[J]. ACM Computing Surveys , 2014, 47 (1) : 3 |
| [4] | RESNICK P, IACOVOU N, SUCHAK M, et al. GroupLens: an open architecture for collaborative filtering of netnews[C]//Proc of the ACM Conference on Computer Supported Cooperative Work. New York, USA: ACM, 1994:175-186. http://cn.bing.com/academic/profile?id=2155106456&encoded=0&v=paper_preview&mkt=zh-cn |
| [5] | BREESE J S, HECKERMAN D, KADIE C. Empirical analysis of predictive algorithms for collaborative filtering[C]//Proc of the 14th Conference on Uncertainty in Artificial Intelligence. San Francisco, USA: Morgan Kaufmann Publishers Inc, 1998:43-52. http://cn.bing.com/academic/profile?id=2110325612&encoded=0&v=paper_preview&mkt=zh-cn |
| [6] |
吴湖, 王永吉, 王哲, 等. 两阶段联合聚类协同过滤算法[J].
软件学报 , 2010, 21 (5) : 1042-1054 WU Hu, WANG Yongji, WANG Zhe, et al. Two-phase collaborative filtering algorithm based on co-clustering[J]. Journal of Software , 2010, 21 (5) : 1042-1054 DOI:10.3724/SP.J.1001.2010.03758 |
| [7] |
杨兴耀, 于炯, 吐尔根·伊布拉音, 等. 融合奇异性和扩展过程的协同过滤模型[J].
软件学报 , 2013, 24 (8) : 1868-1884 YANG Xingyao, YU Jiong, IBRAHIM Turgun, et al. Collaborative filtering model fusing singularity and diffusion process[J]. Journal of Software , 2013, 24 (8) : 1868-1884 |
| [8] |
林耀进, 胡学钢, 李慧宗. 基于用户群体影响的协同过滤推荐算法[J].
情报学报 , 2013, 32 (3) : 299-305 LIN Yaojin, HU Xuegang, LI Huizong. Collaborative filtering recommendation algorithm based on user group influence[J]. Journal of the China Society for Scientific and Technical Information , 2013, 32 (3) : 299-305 |
| [9] |
张佳, 林耀进, 林梦雷, 等. 基于目标用户近邻修正的协同过滤算法[J].
模式识别与人工智能 , 2015, 28 (9) : 802-810 ZHANG Jia, LIN Yaojin, LIN Menglei, et al. Target users neighbors modification based collaborative filtering[J]. Pattern Recognition and Artificial Intelligence , 2015, 28 (9) : 802-810 |
| [10] | SARWAR B, KARPIS G, KONSTAN J, et al. Item-based collaborative filtering recommendation algorithms[C]//Proc of the 10th International Conference on World Wide Web. New York, USA: ACM, 2001: 285-295. |
| [11] | KALELI C. An entropy-based neighbor selection approach for collaborative filtering[J]. Knowledge-Based Systems , 2014, 56 : 273-280 DOI:10.1016/j.knosys.2013.11.020 |
| [12] | JAMALI M, ESTER M. TrustWalker: a random walk model for combining trust-based and item-based recommendation[C]//Proc of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2009: 397-406. http://cn.bing.com/academic/profile?id=2084527756&encoded=0&v=paper_preview&mkt=zh-cn |
| [13] | ZHANG J, LIN Y, LIN M, et al. An effective collaborative filtering algorithm based on user preference clustering[J]. Applied Intelligence , 2016, 45 (2) : 230-240 DOI:10.1007/s10489-015-0756-9 |
| [14] |
黄创光, 印鉴, 汪静, 等. 不确定近邻的协同过滤推荐算法[J].
计算机学报 , 2010, 33 (8) : 1369-1377 HUANG Chuangguang, YIN Jian, WANG Jing, et al. Uncertain neighbors' collaborative filtering recommendation algorithm[J]. Chinese Journal of Computers , 2010, 33 (8) : 1369-1377 DOI:10.3724/SP.J.1016.2010.01369 |
| [15] |
张佳, 林耀进, 林梦雷, 等. 基于信息熵的协同过滤算法[J].
山东大学学报(工学版) , 2016, 46 (2) : 43-50 ZHANG Jia, LIN Yaojin, LIN Menglei, et al. Entropy-based collaborative filtering algorithm[J]. Journal of Shandong University(Engineering Science) , 2016, 46 (2) : 43-50 |
| [16] | BOBADILLA J, HERNANDO A, ORTEGA F, et al. Collaborative filtering based on significances[J]. Information Sciences , 2012, 185 (1) : 1-17 DOI:10.1016/j.ins.2011.09.014 |



