空气预热器(简称空预器)是锅炉的必要设备, 四分仓空预器由于可以减少锅炉漏风, 应用越来越广泛[1]。国内外学者对空预器的热力特性进行大量研究。前人的工作主要集中在空预器出口烟温及风温计算, 内部流体及换热元件温度场计算。在计算出口温度时, 可屏蔽转子参数, 适用于工程应用[1-4]。目前温度场计算方法为将柱坐标下的空预器控制方程通过假设化简为二维模型, 然后求数值解[5-8]。冷伟等人基于解析方法推导得到理论解法, 缺点是以流体及受热面温度线性变化为假设[9]。以上模型都没有考虑漏风对热力性能的影响, 而且主要针对三分仓空预器。漏风一直是回转式空预器热力特性中不可忽视的问题[10]。直接漏风是空预器漏风的最主要形式, 文献[11-14]对直接漏风的漏风间隙、压降规律等做数值模拟。目前的漏风模型都是假设各种漏风的风向, 通过求解质量和能量方程组得到, 但只针对二分仓或三分仓空预器, 并且在密封间隙等重要参数上做了简化假设, 对于四分仓空预器计算, 会带来较大误差[15]。本研究针对四分仓空预器建立综合热力和漏风的计算模型, 弥补以往模型随着四分仓空预器的发展呈现出的局限性, 对比三分仓与四分仓空预器在漏风上的优劣, 分析空预器内部温度分布特点, 评估发生低温腐蚀的可能性。
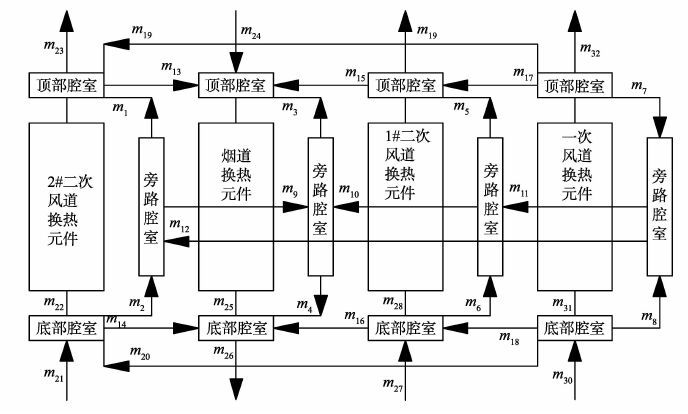
1 计算模型 1.1 物理模型模型由两部分组成, 一是空预器内部热力模型, 二是综合漏风模型。与其他空预器模型相比, 本研究综合考虑热力性能和漏风影响, 对热力和漏风计算采用先独立后联系的方法。热力计算针对空预器内部换热, 漏风计算针对腔室之间的漏风, 然后通过各通道进出口条件将两种计算联系起来。见图 1。
|
图 1 物理模型示意图 Figure 1 Schematic diagram of physical model |
图 1中, 4个大方块代表四分仓空预器分仓, 内部热力模型即计算这4个仓内的温度分布, 其余12个小方块为漏风腔室, 假设每个分仓都有一个旁路腔室、顶部腔室和底部腔室, 漏风只发生在漏风腔室之间, 箭头代表漏风方向, 且每个腔室内的气体都能迅速混合均匀。四分仓空预器漏风情况复杂, 一般分为压力漏风和携带漏风。其中携带漏风由回转式空预器工作特点决定, 占比较小, 因此忽略不计。压力漏风分为径向漏风、周向漏风和轴向漏风。径向漏风为顶部腔室之间或底部腔室之间的漏风, m13~m20;轴向漏风为旁路腔室之间的漏风, m9~m12;周向漏风为底部、顶部腔室与旁路腔室之间的漏风, m1~m8。其中, 周向漏风方向与各旁路腔室压力有关, 需要经过计算确定。
1.2 求解热力模型回转空预器热控制方程:
| $\begin{array}{*{35}{l}} {{w}_{g}}{{\rho }_{g}}{{c}_{p}}\left( 1-{{\varphi }_{z}} \right)\frac{\partial {{T}_{g}}}{\partial z}+\omega {{\sigma }_{m}}{{\rho }_{m}}{{c}_{m}}\frac{\partial {{T}_{m}}}{\partial \theta }- \\ \lambda \left[ {{\varphi }_{z}}\frac{{{\partial }^{2}}{{T}_{m}}}{\partial {{z}^{2}}}+{{\varphi }_{\theta }}\frac{1{{\partial }^{2}}{{T}_{m}}}{{{r}^{2}}\partial {{\theta }^{2}}}+{{\varphi }_{r}}\left( \frac{1\partial {{T}_{m}}}{r\partial r}+\frac{{{\partial }^{2}}{{T}_{m}}}{\partial {{r}^{2}}} \right) \right]=0, \text{ }\left( 1 \right) \\ \end{array}$ | (1) |
| $-{{w}_{g}}{{\rho }_{g}}{{c}_{p}}(1-{{\varphi }_{z}})\frac{\partial {{T}_{g}}}{\partial z}-\alpha \beta ({{T}_{g}}-{{T}_{m}})=0, \text{ }$ | (2) |
式中, 下标g为烟气, m为换热元件;w 为烟气流速, m/s; ρ为密度,kg/m3;c为比热容, kJ/(kg·K);ω为转速, rad/s;T为温度, ℃;σm为换热元件体积分数;θ为转子转动角度, (°);z为换热元件高度, m;r为转子半径, m;φ为换热元件横截面分数;α为对流换热系数, W/(m2·K); β为换热面积, m2。
式(1) 中, 左边三项分别为烟气放热量, 换热元件吸热量及换热元件3个方向导热量, 本研究只考虑轴向导热量, 即只考虑第一项。由文献[8]可知, 温度分布沿半径方向不变。由于假设腔室内气体迅速混合均匀, 因此进口质量流量分布是均匀的, 由此可将上述三维方程简化为二维模型, 并离散求解。
1.3 漏风模型压力漏风量
| $m={{C}_{d}}{{A}_{i}}Y\sqrt{2{{\rho }_{i}}\Delta {{p}_{i}}}, $ | (3) |
式中Cd为排放系数;Ai为漏风面积, m2;Y为气体膨胀系数;ρi为漏风密度, kg/m3;Δpi为压差, Pa。根据文献[15], Cd取0.8, Y取1。
模型中, 每个腔室都可列出质量与能量平衡方程, 加上式(3) , 共得44个方程。未知量为所有漏风量;顶部、底部腔室温度;旁路腔室温度及压力;一、二次风实际进风量, 烟气实际出口流量;实际通过换热元件的气体流量, 总共44个未知量。
由于方程未知量多, 且为非线性方程组, 周向漏风的风向不确定, 因此直接求解此模型十分困难。可采取先求解轴向-周向漏风模型, 再求径向漏风, 迭代计算的方法, 简化求解过程。
1.4 漏风模型与热力模型耦合漏风模型与热力模型的耦合是一个迭代过程, 先忽略漏风求解热力模型, 根据热力模型结果求解漏风模型, 再由漏风模型求出的新参数来回代到热力模型中去, 直至满足精度要求。计算流程见图 2。

|
图 2 计算流程图 Figure 2 Calculation flow chart |
以哈尔滨锅炉厂某四分仓空预器为例, 已知参数见表 1。
| 表 1 已知参数 Table 1 Known parameters |
表 2为网格独立性验证, 可见在800个网格以上结果偏差很小, 因此选择800个网格进行计算。
| 表 2 网格独立性验证 Table 2 Mesh independence verification |
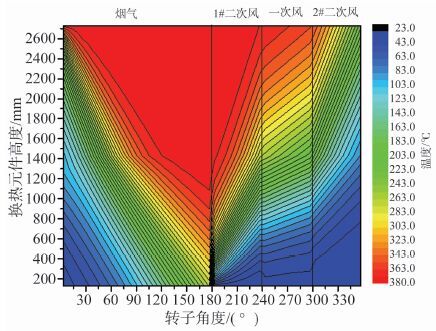
图 3为稳定状态时各通道流体的温度分布等值线图, 可以清晰地看到, 在各通道内温度变化层次鲜明, 等温线近似平行。各通道内虽然工质、流量、入口温度不同, 但温度分布是连续的, 局部的最低排烟温度略高于进口风温的, 在这些部位的烟温及换热元件温度都较低, 容易发生低温腐蚀。
|
图 3 流体温度分布图 Figure 3 Fluid temperature field |
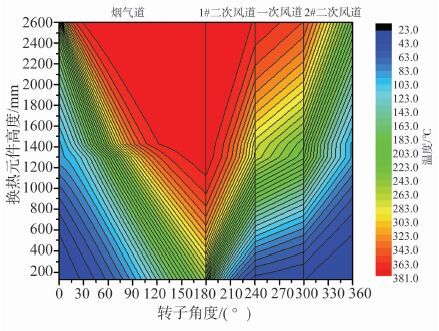
图 4为换热元件温度分布等值线图, 换热元件的温度场与流体的温度场十分相似, 整个温度场等温线近似为“V”型分布。通过计算, 热段换热元件平均温度为313.3℃, 冷段为158.1℃, 因此为了提高换热效率, 冷热端应采取不同的板型, 尤其是冷段需防止低温腐蚀。从图 4中可见, 比例较大的高温区域中, 与流体基本没有换热, 因此, 为了更好地促进换热, 同时防止烟气道冷段低温区域过大, 需合理地分配流体进口流量分布, 应当沿转子方向流量逐渐降低。
|
图 4 换热元件温度分布图 Figure 4 Matrix temperature field |
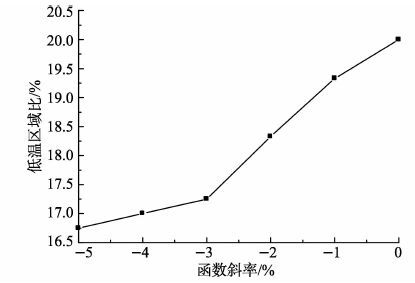
为更清晰地评估换热元件的低温腐蚀可能性, 定义低温区域比的概念, 即换热元件温度低于100℃的计算网格数量与总网格数量之比。假设烟气进口流量与转动角度为线性函数关系, 图 5为低温区域比与函数斜率的关系。由图 5可知, 函数斜率越大, 即沿转动方向流量递减梯度越大;低温区域比越小, 发生低温腐蚀的几率也越小。
|
图 5 低温区域比与函数斜率关系图 Figure 5 Relation graph of low-temperature area and funtion dope |
同时, 烟气平均出口温度为115.29℃, 与设计值112℃相对误差为2.94%;一次风平均出口温度为361.69℃, 与设计值345.55℃相对误差为4.67%;二次风平均出口温度为328.66℃, 与设计值342.2℃相对误差为-3.96%, 均在允许范围内。
各处漏风的漏风量见表 3。根据定义, 漏风率为漏入烟气侧的空气量除以空预器入口总烟气量。计算得漏风率为2.13%与哈尔滨锅炉厂提供漏风率2.42%一致。
| 表 3 各处漏风量 Table 3 Air leakage mass flow kg/s |
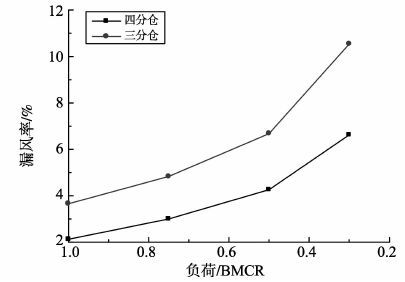
为了对比四分仓与三分仓空预器的漏风情况, 将此四分仓空预器的两个二次风仓合并, 当作三分仓进行计算, 图 6为不同负荷下, 三分仓与四分仓空预器的漏风率变化, 计算了30%、50%、75%和100%锅炉最大连续蒸发量(bolier maximum continue rate, BMCR)工况下的漏风情况。可见, 随着负荷的降低, 三分仓与四分仓空预器的漏风率都呈上升趋势, 但四分仓空预器的漏风率始终比三分仓低。这是由于两个二次风仓将压力最高的一次风与压力最低的烟气隔离, 降低空气与烟气漏风处的压力差, 从而减少了漏风。
|
图 6 不同负荷下三分仓与四分仓空预器漏风率对比 Figure 6 The comparison of air leakage rate between tri-sectional and quad-sectional air preheater under different load |
建立了四分仓空预器的热力及漏风计算模型, 并进行耦合计算。与实际空预器验证, 结果准确, 可为空预器的设计、制造和运行提供指导。经计算发现, 在各种负荷下, 四分仓空预器的漏风率均显著低于三分仓空预器。空预器内流体与换热元件的温度分布基本一致, 等温线分布呈“V”型, 且各通道间流体温度分布是连续的, 并不因流量或流体种类而间断。烟气进口量流量沿转动方向的递减可以显著地降低低温区域比, 且递减梯度越大, 效果越明显, 从而降低低温腐蚀可能性。
| [1] |
陈昌贤, 孙奉仲, 李飞, 等. 四分仓回转式空气预热器热力计算方法[J].
山东大学学报(工学版) , 2014, 44 (4) : 60-65 CHEN Changxian, SUN Fengzhong, LI Fei, et al. Thermal calculation method for quad-sectional regenerative air preheater[J]. Journal of Shandong University (Engineering Science) , 2014, 44 (4) : 60-65 |
| [2] |
周俊虎, 杨卫娟, 靳彦涛, 等. 三分仓空气预热器热力计算的研究[J].
动力工程 , 2003, 23 (6) : 2810-2813 ZHOU Junhu, YANG Weijuan, JIN Yantao, et al. Research of tri-sectional air preheater thermal calculation[J]. Power Engineering , 2003, 23 (6) : 2810-2813 |
| [3] |
冷伟, 王渡. 一种改进的回转式空气预热器热力计算方法[J].
动力工程 , 2005, 25 (3) : 392-395 LENG Wei, WANG Du. An improved way for thermal calculation of rotary air preheater[J]. Power Engineering , 2005, 25 (3) : 392-395 |
| [4] |
郑凯, 周克毅, 黄军林, 等. 一种改进的三分仓空气预热器热力计算方法[J].
动力工程学报 , 2012, 32 (1) : 31-35 ZHENG Kai, ZHOU Keyi, HUANG Junlin, et al. An improved thermal calculation method for tri-sectional rotary air preheaters[J]. Journal of Chinese Society of Power Engineeryin , 2012, 32 (1) : 31-35 |
| [5] | SKIEPKO T, SHAH R K. A comparison of rotary regenerator theory and experimental results for an air preheater for a thermal power plant[J]. Experimental Thermal and Fluid Science , 2004, 28 (28) : 257-264 |
| [6] |
张启, 王谦, 王恩禄, 等. 基于有限差分的二分仓回转式空气预热器热力计算[J].
锅炉技术 , 2009, 40 (4) : 25-29 ZHANG Qi, WANG Qian, WANG Enlu, et al. Bisector air preheater performance evaluation based on numerical finite difference method[J]. Boiler Technology , 2009, 40 (4) : 25-29 |
| [7] |
刘福国, 周新刚. 考虑轴向导热的三分仓回转预热器传热模型及验证[J].
机械工程学报 , 2010, 46 (22) : 144-150 LIU Fuguo, ZHOU Xingang. Heat transfer model of tri-section rotary air preheater and experimental verification[J]. Journal of Mechanical Engineering , 2010, 46 (22) : 144-150 DOI:10.3901/JME.2010.22.144 |
| [8] | HEIDARI-KAYDAN A, HAJIDAVALLOO E. Three-dimensional simulation of rotary air preheater in steam power plant[J]. Applied Thermal Engineering , 2014 (73) : 399-407 |
| [9] |
冷伟, 陈道轮, 张志伦, 等. 基于解析方法的回转式空气预热器换热计算[J].
中国电机工学报 , 2005, 25 (3) : 141-146 LENG Wei, CHEN Daolun, ZHANG Zhilun, et al. Heat exchange calculation of regenerative air preheater with analytical method[J]. Proceeding of the CSEE , 2005, 25 (3) : 141-146 |
| [10] | SKIEPKO T. Experimental results concerning seal clearances in some rotary heat exchangers[J]. Heat Recovery Systems , 1988, 8 (6) : 577-871 DOI:10.1016/0890-4332(88)90017-8 |
| [11] | ZENG M, DU L, LIAO D, et al. Investigation on pressure drop and heat transfer performances of plate-fin iron air preheater unit with experimental and genetic algorithm methods[J]. Applied Energy , 2012, 92 (4) : 725-732 |
| [12] | WANG L, DENG L, TANG C, et al. Thermal deformation prediction based on the temperapture distribution of the rotor in rotary air-preheater[J]. Applied Thermal Egineering , 2015, 90 : 478-488 DOI:10.1016/j.applthermaleng.2015.07.021 |
| [13] | CAI M, HUI S, WANG X, et al. A study on the direct leakage of rotary air preheater with multiple seals[J]. Applied Thermal Engineering , 2013, 59 (1-2) : 576-586 DOI:10.1016/j.applthermaleng.2013.05.049 |
| [14] | JESTIN L, FULS W, PRONOBIS M. A numerical study of air preheater leakage[J]. Energy , 2015, 92 : 37-44 |
| [15] | SHAH R K, SKIEPKO T. Influence of leakage distribution on the thermal performance of a rotary regenerator[J]. Applied Thermal Engineering , 1999, 19 : 685-705 DOI:10.1016/S1359-4311(98)00087-8 |




