桥梁在大中型城市交通中扮演着重要角色, 但地震等自然灾害经常导致桥梁结构破坏甚至倒塌。怎样提高桥梁结构抗震性能已经成为我国桥梁建设领域亟待解决的重大课题[1-2]。桥梁的倒塌往往由桥墩的破坏所引起, 故研究包括桥墩倒塌的非线性地震反应是钢筋混凝土桥梁抗震设防的重中之重[3-5], 而对桥墩进行延性抗震性能分析是现今抗震设计的主要思路。
在研究桥墩延性抗震性能时, Pushover是一种较简便的分析方法。Pushover分析也称为静力弹塑性分析, 是一种进行结构地震反应分析的简化方法, 在桥梁结构抗震分析与设计中得到了广泛应用[6-7]。一般意义上的Pushover分析, 是通过对要分析的结构模型施加某种分布的水平力, 将结构推至目标位移或使结构成为机构, 分析结构的非线性行为[8-9]。在传统的Pushover分析过程中, 水平侧向荷载一般是单方向单调递增的[10]。而结构受到地震力是往复作用荷载, 单方向的加载方式无法准确地模拟地震作用下结构和构件的真实受力情况[11], 故本研究采用基于循环往复的Pushover分析方法研究圆柱桥墩的延性破坏过程。通过改变墩顶竖向荷载研究轴压比变化对圆柱桥墩的延性能力的影响。
1 材料本构模型 1.1 混凝土本构模型对于无约束混凝土, 因其最大压应变值过小, 难以满足桥墩塑性转动能力所需要的结构应变。如钢筋混凝土桥墩采用无约束混凝土模型, 当塑性铰区截面混凝土处于极限状态的压应变时, 整个桥墩就会达到破坏极限状态, 这对于延性结构设计是不适合的[1-13]。Mander混凝土本构模型可以考虑下面几方面问题:起约束作用的横向箍筋对混凝土受压骨架曲线的峰值应变、应力和极限压应变的提高作用;混凝土的抗拉、开裂等特性[14-15]。
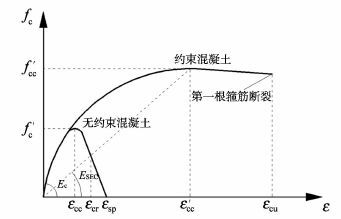
本研究分析中, 约束和无约束混凝土采用Mander混凝土本构模型, 其受压骨架曲线如图 1所示(其中, εcc为无约束混凝土的峰值压应变; εcr为无约束混凝土的压碎应变;εsp为无约束混凝土的剥落应变;ε′cc为约束混凝土的峰值压应变;εcu为约束混凝土的极限压应变;f′c为混凝土圆柱体抗压强度;f′cc为约束混凝土峰值压应力;Ec为混凝土切线弹性模量;Esec为约束混凝土峰值割线模量)。
|
图 1 Mander提出的约束和无约束混凝土受压骨架曲线 Figure 1 The compressed backbone curve of confined and |
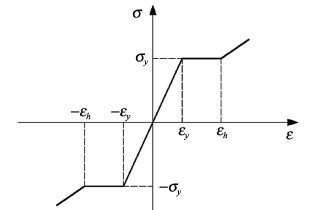
本研究采用了如图 2所示的钢筋本构模型, 该力学模型考虑了钢筋加载到后期的材料强化行为, 平台段表示的是钢筋屈服到强化阶段, 适用于模拟应变值较大时钢筋的应力-应变曲线[16], 这种力学模型是当前钢筋混凝土的截面计算中运用非常广泛的一种计算模型。
|
图 2 钢筋本构模型 Figure 2 The model of reinforcing steel |
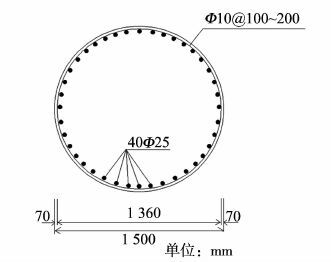
该桥墩为圆柱形桥墩, 直径1500mm, 横截面见图 3所示, 单位为mm。
|
图 3 桥墩横截面 Figure 3 Cross-section of pier |
该桥墩采用C30混凝土, 纵筋采用HRB400, 箍筋采用HPB300, 主要设计参数见表 1。
| 表 1 桥墩参数 Table 1 Pier parameters |
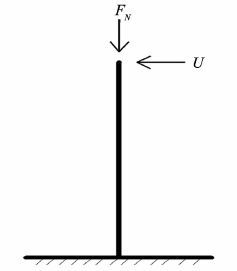
圆柱桥墩模型与承台的边界, 可认为刚接;墩顶耦合一个参考点, 在参考点上施加低周反复的水平荷载, 在运行时采用两个荷载步来实现, 加载图如图 4所示。首先通过压强作用方式在墩顶施加恒定的竖向荷载来模拟轴压;然后通过位移加载方式在墩顶施加横桥向的反复水平荷载, 循环加载制度由amplitude加载幅值命令来实现[17-18], 荷载施加情况简化如图 5示。
|
图 4 桥墩加载示意图 Figure 4 Loading schematic of pier |
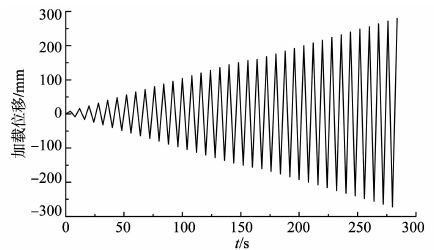
|
图 5 侧向位移往复加载规则 Figure 5 Rule of lateral displacement reciprocating load |
目前, 钢筋混凝土柱式桥墩在公路桥梁中得到广泛应用, 通常采用矩形、圆形和矩形带圆端等截面形式;纵向钢筋一般的配筋率1%~3%;混凝土强度等级C20~C40;轴压比0.10~0.30。
本研究主要考虑单个桥墩的六级轴向压力, 分别对应轴压比0.20、0.22、0.24、0.26、0.28、0.30六种情况, 对比分析轴压比变化对该圆柱桥墩延性性能的影响, 其它参数参照表 1所示并保持不变。
当轴压比分别为0.20、0.22、0.24、0.26、0.28、0.30时, 按照上述加载方案对桥墩模型加载, 计算桥墩应力过程, 图 6为轴压比为0.24时圆柱墩钢筋与混凝土首次屈服应力云图。汇总箍筋、纵筋和混凝土首次屈服时间如表 2所示。
由表 2分析可得, 随着轴压比的变化, 保护层混凝土、纵筋达到首次屈服的时间并无明显规律可循, 但轴压比大于0.26时箍筋的首次屈服时间随轴压比的增加明显加速提前。核心区混凝土的屈服是桥墩失效的重要标志, 本研究通过极限位移的出现来判断核心区混凝土的屈服, 即墩顶达到极限位移时核心区混凝土受压屈服。
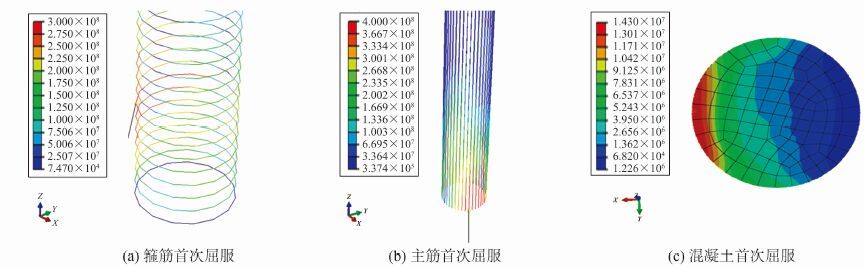
|
图 6 轴压比为0.24时圆柱墩钢筋与混凝土首次屈服应力云图 Figure 6 First yield stress cloud of cylindrical pier's steel and concrete under axial compression ratio 0.24 |
| 表 2 桥墩各部分在不同轴压比下首次屈服时间 Table 2 Each part of the pier for the first yield time under different axial compression ratio |
根据计算结果分别绘制出了轴压比为0.20、0.22、0.24、0.26、0.28、0.30时墩顶施加的侧向力F和墩顶侧向位移D曲线(即滞回曲线)如图 7中的各工况所示。
由图 7中滞回曲线可以看出, 模型从开始加载到一定阶段, 骨架曲线几乎是直线, 即荷载和位移线性相关, 表明此阶段模型正处于弹性阶段;当模型继续加载, 荷载-位移曲线加载段走势开始平缓, 斜率逐渐变小, 表明荷载随位移增长幅度变慢, 此时结构刚度已有所降低, 结构处于非弹性阶段。对比滞回曲线1~6可以发现, 当轴压比从0.20增加到0.30时, 滞回环随着位移加载的变大, 倾倒现象明显, 且滞回环后期随着轴压比的增大, 更加地趋于扁平化。
将上述六个滞回曲线各滞回环的峰值连接起来, 得到如图 8所示的桥墩的侧向力F和侧向位移D骨架曲线。
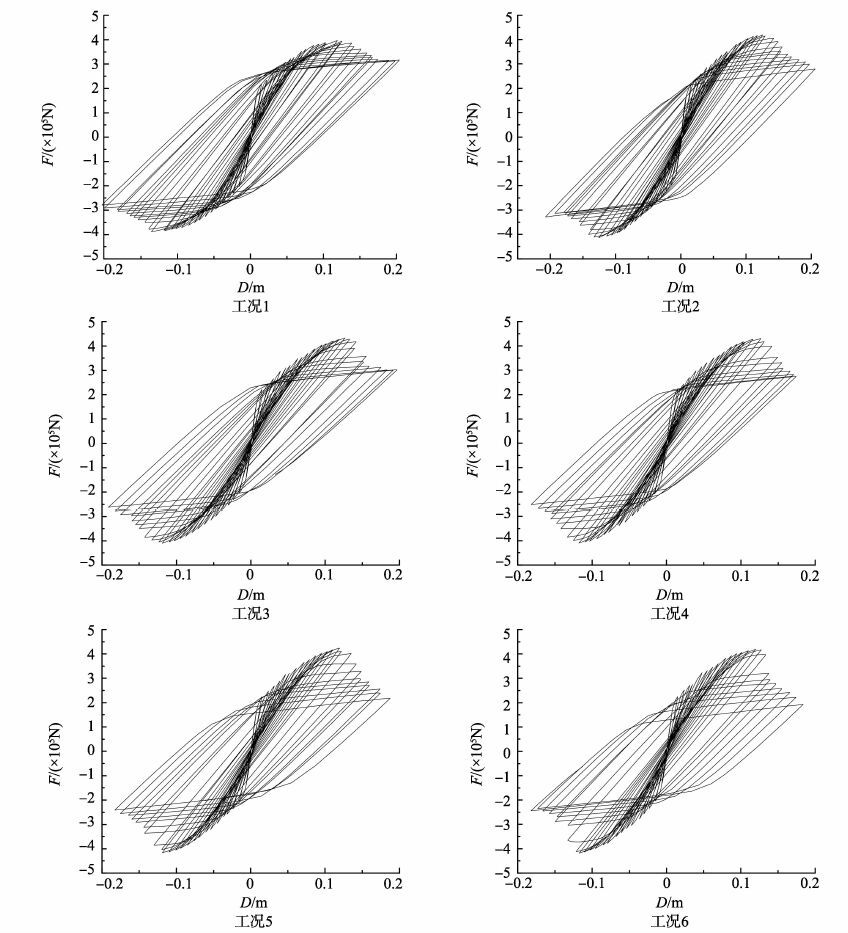
|
图 7 各工况下墩顶侧向力与位移的滞回曲线 Figure 7 Hysteresis curve of pier top lateral force and displacement under each condition |
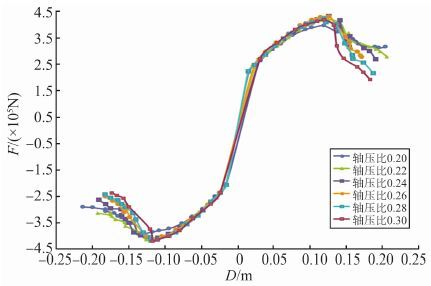
|
图 8 不同轴压比下桥墩顶部荷载-位移骨架曲线对比 Figure 8 Contrast of top pier load-displacement skeleton curves under different axial compression ratio |
对比图 8在不同轴压比下的骨架曲线可知, 轴压比较小时, 骨架曲线受轴压比影响不大, 当轴压比超过0.26时, 承载力下降迅速。
通过作图法求得该圆柱桥墩的屈服荷载与屈服位移, 骨架曲线峰值点对应极限荷载和位移峰值, 定义在骨架曲线极限荷载下降后的85%为破坏荷载[19], 对应的位移为极限位移。
汇总图 8中的数据, 得到桥墩的屈服荷载、屈服位移、极限荷载、峰值位移、破坏荷载、极限位移以及位移延性系数, 如表 3所示。
| 表 3 圆柱桥墩骨架曲线各特征值 Table 3 Feature values of pillar piers' skeleton curve |
(1) 随着轴压比的增大, 极限位移逐渐减小, 对应的核心区混凝土的屈服时间也越短。
(2) 圆柱墩的位移延性系数随轴压比的增大而减小。
(3) 当轴压大于0.26时, 随着轴压比增大, 桥墩的屈服荷载和屈服位移也增大。
(4) 轴压比较大时, 延性性能较差, 骨架曲线下降较快, 当超过极限荷载后, 下降趋势更加明显。轴压比较小时, 延性性能较佳, 骨架曲线下降速度慢, 较为平缓。
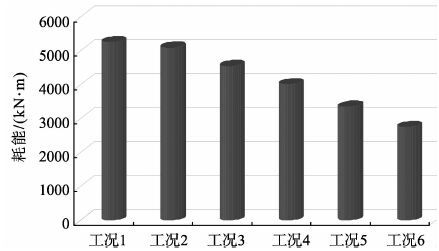
通过图 7的滞回曲线, 通过软件可计算获得每种轴压比条件下的圆柱墩的累积耗能情况, 得到的柱状图如图 9所示。
|
图 9 各工况下墩柱累积耗能 Figure 9 Pier's cumulative energy under each condition |
由图 9可见, 当轴压比为0.20时, 圆柱墩累积耗能5267.835kN·m, 轴压比增大到0.30时, 圆柱墩累积耗能2763.542kN·m, 耗能能力下降了47.5%。
3 结论本研究运用有限元软件ABAQUS建立圆柱墩非线性有限元模型, 采用基于循环加载的Pushover分析方法研究了圆柱桥墩的延性破坏过程, 分析了轴压比对圆柱桥墩延性性能的影响。数值分析结果表明:
(1) 轴压比的增大缩短了核心区混凝土屈服的时间, 而对圆柱桥墩保护层混凝土和纵向钢筋首次屈服时间的影响无明显规律可循, 但轴压比大于0.26时箍筋的首次屈服时间随轴压比的增加明显加速提前。
(2) 在轴压比大于0.26时, 随着轴压比增大, 桥墩的屈服荷载和屈服位移也增大。
(3) 圆柱墩的位移延性系数随轴压比的增大而减小。
(4) 随着轴压比的增大, 圆柱墩的滞回耗能能力降低。从轴压比0.20增大到轴压比0.30, 圆柱墩的滞回耗能能力降低了近五成。故选择合适的轴压比可以提高桥墩的延性性能, 进而提高桥墩的抗倒塌能力。
| [1] | 秦泗凤. 桥梁抗震性能评价的静力非线性分析方法研究[D].大连:大连理工大学, 2008.QIN Sifeng. Static nonlinear analysis methods for estimating seismic performance for bridges[D]. Dalian:Dalian University of Technology, 2008. |
| [2] | 吕国栋. 基于Pushover分析的城市高架桥梁抗震性能评估[D]. 兰州:兰州交通大学, 2012.L Guodong. Seismic assessment of urban elevated bridges based on pushover analysis[D]. Lanzhou:Lanzhou Jiaotong University, 2012. |
| [3] | 孙鹏, 罗韧, 李鸿晶, 等. 地震作用下混凝土梁桥连续倒塌过程分析[J]. 空间结构 , 2015, 21 (1) : 78-84 |
| [4] | 赵岩. 桥梁抗震的线性/非线性分析方法研究[D]. 大连:大连理工大学, 2003.ZHAO Yan. On linear/nonlinear seismic analysis mothods of bridges[D]. Dalian:Dalian University of Technology, 2003. |
| [5] | 莎玛.基于试验的矩形空心墩抗震性能研究[D].西安:长安大学, 2011.SHEIMAA I M. Experimental study on seismic behavior of rectangular hollow pier[D]. Xi′an:Chang′an University, 2011. |
| [6] | SHAKERI K, TARBALI K, MOHEBBI M. Pushover analysis of asymmetric-plan buildings based on distribution of the combined modal story shear and torsional moment[J]. Earthquake Engineering and Engineering Vibration , 2014, 13 (4) : 707-716 DOI:10.1007/s11803-014-0274-5 |
| [7] | 盛光祖. Pushover分析方法的发展及其在桥梁结构中的应用[J]. 华北地震科学 , 2008, 26 (4) : 25-30 |
| [8] | 汪大绥, 贺军利, 张凤新. 静力弹塑性分析(Pushover Analysis)的基本原理和计算实例[J]. 世界地震工程 , 2004, 20 (1) : 45-53 |
| [9] |
盛光祖, 李建中, 陈亮. 桥梁单墩不同侧向力分布模式Pushover分析方法[J].
振动与冲击 , 2010, 29 (2) : 170-174 SHENG Guangzu, LI Jianzhong, CHEN Liang. Pushover analysis of different distribute lateral load patterns for seismic assment of bridge piers[J]. Journal of Vibration and Shock , 2010, 29 (2) : 170-174 |
| [10] |
叶献国, 种迅, 李康宁, 等. Pushover方法与循环往复加载分析的研究[J].
合肥工业大学学报(自然科学版) , 2001, 24 (6) : 1019-1024 YE Xianguo, ZHONG Xun, LI Kangning, et al. Study on Pushover analysis procedure and reversal load pattern[J]. Journal of Hefei University of Technology(Natural Science) , 2001, 24 (6) : 1019-1024 |
| [11] |
侯爱波, 汪梦甫. 循环往复加载的Pushover分析方法及其应用[J].
湖南大学学报(自然科学版) , 2003, 30 (3) : 145-147 HOU Aibo, WANG Mengfu. The analysis method and application of circulating Pushover[J]. Journal of Hunan University(Natural Science) , 2003, 30 (3) : 145-147 |
| [12] |
谢海清, 杨国静, 何庭国. 铁路矩形空心桥墩延性抗震设计简化计算方法[J].
世界地震工程 , 2010, 26 (1) : 147-152 XIE Haiqing, YANG Guojing, HE Tingguo. Simplified method for ductile seismic design of railway rectangular hollow piers[J]. World Earthquake Engineering , 2010, 26 (1) : 147-152 |
| [13] | 任士朴. FRP约束钢筋混凝土桥墩抗震性能研究[D]. 西安:长安大学, 2014.REN Shipu.The study of the seismic performance of the FRP confined concrete bridge columns[D]. Xi′an: Chang′an University, 2014. |
| [14] |
齐虎, 李云贵, 吕西林. 箍筋约束混凝土单轴滞回本构实用模型[J].
工程力学 , 2011, 28 (9) : 95-102 QI Hu, LI Yungui, LYU Xilin. A practical confined concrete constitutive model under uniaxial hysteresis load[J]. Engineering Mechanics , 2011, 28 (9) : 95-102 |
| [15] | 艾庆华. 钢筋混凝土桥墩抗震性态数值评价与试验研究[D].大连:大连理工大学, 2008.AI Qinghua.Numerical evaluation and experimental study of seismic performance for reinforced concrete bridge piers[D].Dalian:Dalian University of Technology, 2008. |
| [16] |
王强, 朱丽丽, 李哲, 等. ABAQUS显式分析梁单元的混凝土、钢筋本构模型[J].
沈阳建筑大学学报(自然科学版) , 2013, 29 (1) : 56-64 WANG Qiang, ZHU Lili, LI Zhe, et al. Study on the constitutive model of concrete and steel for explicit dynamic beam elements of ABAQUS[J]. Journal of Shenyang Jianzhu University (Natural Science) , 2013, 29 (1) : 56-64 |
| [17] | 董浩然. FRP约束钢筋混凝土桥墩抗震性能分析[D].大连:大连理工大学, 2015.DONG Haoran.Analytical seismic performance of FRP confined RC bridge pier[D]. Dalian:Dalian University of Technology, 2015. |
| [18] |
杜修力, 陈明琦, 韩强. 钢筋混凝土空心桥墩抗震性能试验研究[J].
振动与冲击 , 2011, 30 (11) : 254-259 DU Xiuli, CHEN Mingqi, HAN Qiang. Experimental evaluation of seismic performance of reinforced concrete hollow bridge columns[J]. Journal of Vibration and Shock , 2011, 30 (11) : 254-259 |
| [19] |
叶列平. 高强砼框架柱抗震性能的试验研究[J].
建筑结构学报 , 1992, 13 (4) : 41-48 YE Lieping. Experimental research on earthquake resistance behavior of high-strength concrete frame columns[J]. Journal of Architectural Structure , 1992, 13 (4) : 41-48 |




