2. 四川省遂宁市水务局,四川 遂宁 629000
2. Suining Water Authority of Sichuan Province, Suining 629000, Sichuan, China
我国的水库大坝、江河大堤大部分为土坝、土堤,如果这些工程坝体的变形稳定和渗流稳定得不到保证,将影响水利枢纽的安全运行[1]。
目前,土坝边坡稳定的分析方法主要有传统的极限平衡方法和数值分析方法[2-4]。极限平衡法是较早应用的一种边坡稳定分析的方法,该方法以摩尔-库伦强度准则为基础,根据条分边坡体后的垂直力的平衡方程,求解安全系数,分析边坡稳定性[5]。数值分析法是近年来应用较多的计算边坡稳定的方法,数值方法能很好地考虑土体中应力与应变的关系。1975年, ZIENKIEWICZ O C首先将抗剪强度折减系数的概念应用于弹塑性有限元稳定数值分析中,经过算例证明,运用此种方法做出的强度储备安全系数和极限平衡法的毕肖普法求得的稳定安全系数相吻合[6-9]。
本研究依据有限元的强度折减法的基本原理,针对渠河河堤跨河大桥桩基施工对河堤安全的影响进行计算分析,对坝体加固方案和桩基施工提出合理的建议。
1 数值方法基本原理有限元强度折减法数值分析的原理是将材料的强度参数粘聚力和内摩擦角均除以折减系数,得到新的强度参数,将新的强度参数赋给数学模型后,试算此时模型的稳定性[10-11]。不断增大折减系数来降低边坡土体的强度参数,反复运算,直至边坡破坏,此时的折减系数就是相应的边坡稳定安全系数。有限元强度折减法优于极限平衡法之处是不需要事先假定滑动面的位置及形状且无需进行条分即可得到坝体的应力、塑性区及变形趋势[12],在有限元计算之后,还可以通过塑性区找到滑动破坏面等[13]。
在边坡稳定分析中,通常采用摩尔-库伦强度准则[14]。对于坝体失稳的判断依据[15-17],工程界目前还没有统一的标准。目前常用的三种判据分别为:(1) 以塑性区(或者等效塑性应变)从坡脚到坡顶贯通作为边坡失稳的判据;(2) 以有限元迭代求解过程的不收敛作为边坡失稳的判据;(3) 以坡体内部特征部位位移突变作为边坡失稳的判据。当数值计算中坡体失稳时, 一般会有一定幅值的塑性区贯通整个坝坡,但塑性区贯穿坝坡并不能决定此时的坝坡已经发生失稳破坏[18-19]。有限元解出现不收敛通常会在使用有限元强度折减法分析边坡稳定性时被视作破坏的标准[20]。
在本次工程实例的计算分析中,采用有限元迭代求解过程的不收敛作为边坡失稳的判据。本研究采用岩土工程有限元计算程序PLAXIS进行模拟计算。PLAXIS程序是由荷兰PLAXIS B.V.公司推出的一系列功能强大的通用岩土有限元计算软件,现在已广泛应用于各种复杂岩土工程项目的有限元分析中,程序适应性强,能够模拟复杂的工程地质条件,尤其适合于变形和稳定分析。
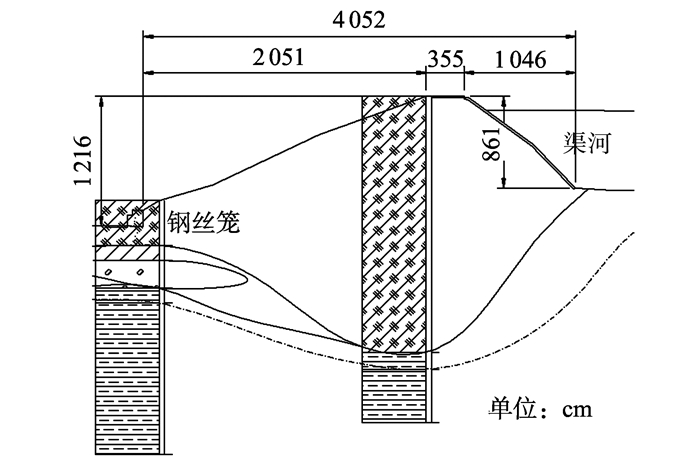
2 工程应用 2.1 工程概况渠河位于四川省遂宁市境内,全长26.6 km,主要为引水渠。在渠河上拟建一座跨河大桥。大桥处渠河左岸为填方渠岸,右岸为基岩挖方渠岸。拟建渠河大桥6#墩正好位于左岸填方渠堤之上。据调查,该处渠堤坝型为均质土坝,填筑料为均质黏土,坝后坡脚设有排水棱体。渠河大桥处渠堤计算断面及常水位如图 1所示。
|
图 1 渠河大桥处渠堤计算断面及常水位 Figure 1 Calculation sector and the constant water level of embankment at Quhe River Bridge |
根据设计,6#墩桩基建造在渠河的左岸坝体之上,桩外径距离迎水面堤顶最近距离约3 m左右。根据桩基施工要求,坝顶路面需加宽到6 m。坝体加宽后,对桥墩桩基进行施工。坝体培土加宽和桩基钻孔取土的施工,均可能对坝体土体稳定性造成影响。根据上述情况,主要进行以下研究:
(1) 对坝体加宽后坝体稳定性进行分析,以确定坝体安全加宽的最佳方案;
(2) 对桩基础施工过程中坝体渗透稳定和边坡结构稳定进行分析,以便对桩基施工方案的确定提供指导意见。
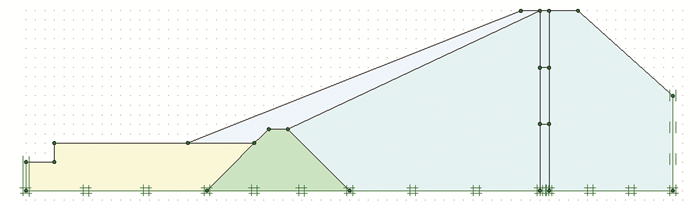
2.2 几何模型及有限元剖分根据勘察、设计单位提供的资料,坝基基底为中风化的砂质泥岩,可以看作是不透水边界,渠河底部岩层层位较高,也作为不透水边界处理。坡体底边固定约束,左右两边水平约束,其他为自由边界。坝后坡设置排水棱体,坝体渗水通过排水棱体排向小河沟。初步拟定坝体后坡培土加宽坡度为1.00:2.12。为便于计算建模,对原断面图按照渗流等效与应力等效[21]的原则进行了概化,构建二维平面应变有限元计算模型,坝体模型几何图形如图 2所示。
|
图 2 坝体模型几何图形示意图 Figure 2 Schematic of the dam model geometry |
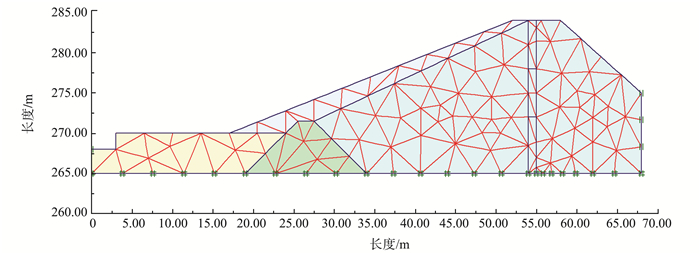
建立模型后,生成有限元模型网格。网格生成过程以可靠三角剖分原理为基础,通过搜索最优三角形单元,生成一个非结构性的网格。模型共剖分189个15节点有限元网格单元,共计1 615个节点,稳定计算坝体有限元模型网格剖分如图 3所示。
|
图 3 有限元模型网格剖分示意图 Figure 3 Schematic of the mesh generation for finite element |
模型材料分为坝体填土区、排水棱体、排水棱体和河沟之间地层区域以及坝后坡加宽区。计算所需各层土体力学参数主要根据地勘资料确定,资料中没有提供的根据经验数据确定, 见表 1。根据本工程实际情况,并结合国内类似土石坝工程培土增厚坝体的经验,坝后坡加宽材料初步采用砂卵石或泥岩石渣等透水材料。
| 表 1 各层土体的力学参数 Table 1 Mechanical parameters of the soil layers |
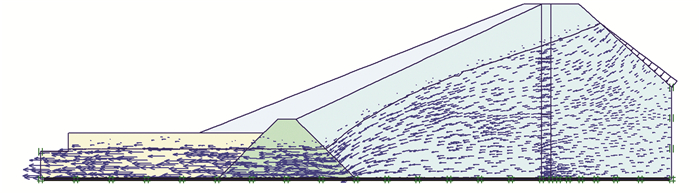
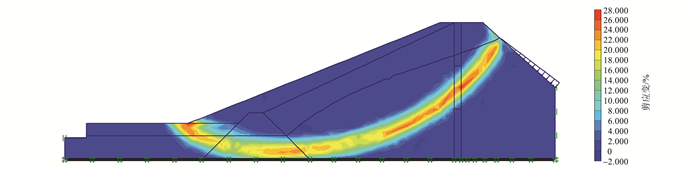
根据初步设计,坝后坡加宽坡度为1.00:2.12。首先计算设计水位情况下坝体渗流场分布,将其作为边界条件施加到坝体单元中,计算在渗流作用下坝体的应力应变,然后用强度折减法对坝坡进行稳定分析,得到加宽坡度为1.00:2.12坝坡的最小稳定安全系数。计算过程中坝体渗流场分布如图 4所示,坝体稳定分析的塑性应变场分布如图 5所示。
|
图 4 渗流场分布矢量图 Figure 4 Vector diagram of seepage field distribution |
|
图 5 坝体塑性应变云图 Figure 5 Plastic strain cloud map of dam |
根据数值模拟计算结果,在有渗流作用下,坝后坡加宽坡度为1.00:2.12时坝体稳定安全系数为1.090。根据《碾压式土石坝设计规范》(SL274—2001)要求,对于4、5级土石坝,正常运行条件下,坝体稳定安全系数为1.150。由此可知,坝坡坡度为1.00:2.12时,坝体稳定安全系数达不到规范要求。
调整后坝坡坡度为1.00:3.00,采用砂卵石材料,重新计算得到放坡后坝体最小稳定安全系数为1.179,坝体将达到稳定状态,同时方案设计较为经济。因此建议坝体加宽采用1.00:3.00的放坡坡度。
2.4.2 桩孔开挖过程中坝体稳定性和桩孔渗流稳定性分析桩孔开挖采用旋转开挖法,桩孔开挖直径1 m。若孔内不用支护,开挖会造成孔位土体应力卸载[22],从而引起坝体应力应变重新分布[23];同时,桩孔开挖后,相当于在坝后坡设置一个大型排水井,同时对坝体渗流场也有所改变。
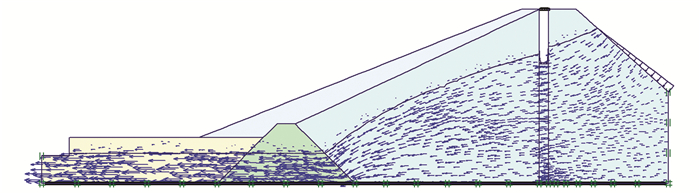
桩孔开挖至8 m时坝体渗流场分布及塑性区分布结果如图 6、7所示。
|
图 6 桩孔开挖至8 m时渗流场分布矢量图 Figure 6 Seepage field distribution vector diagram with the pile hole of 8 m deep |

|
图 7 桩孔开挖至8 m时塑性区分布云图 Figure 7 Plastic zone distribution cloud map with the pile hole of 8 m deep |
分析桩孔开挖过程的数值计算结果可知:桩孔部位如不采取止水及加固措施,渗流就会汇集到孔中,同时在孔壁形成较大的渗透坡降[24],且开挖过程中孔壁最大渗透坡降为0.63~1.00,接近黏性土的临界水力坡降1.00,有发生流土破坏的可能。
根据塑性区分布图(图 7)可以看出,桩孔开挖过程中,孔壁附近发生塑性变形,容易引起孔壁坍塌等破坏[25-26]。
坝体稳定性分析表明,孔口开挖过程中,边坡稳定安全系数均大于1.150,坝坡稳定性可以得到保证。
2.4.3 坝顶作用有施工荷载情况下坝坡稳定性分析在坝坡按照1.00:3.00的坡比加宽后,在原坝顶位置施加施工分布荷载,模拟坝体稳定性。
数值模拟结果表明,当施工分布荷载分别为5、10、15、20、25、30、35 kN/m2时,坝体稳定安全系数分别为1.096、1.086、1.081、1.075、1.069、1.063、1.056。随着荷载的增大,坝体稳定安全系数逐渐变小,坝坡失稳的危险性增大,需对施工荷载进行合理控制。
3 结 语采用有限元强度折减法计算分析边坡稳定性,相对于传统的极限平衡法求解过程简单,计算结果可以满足工程应用要求。通过对渠河河堤跨河大桥桩基工程边坡进行稳定性分析,确定了合理的加宽后的坝坡坡度为1.00:3.00,该坝坡坡度能够满足对坝体稳定性的要求且经济实用;通过对桩基础施工过程桩孔的渗透稳定性的分析,指出桩孔开挖过程中,桩孔孔壁存在渗透破坏的隐患,需采取防护措施;施工过程中坝顶分布荷载也是影响坝坡稳定性的关键因素,需要进行合理控制。研究结果为渠河河堤跨河大桥桩基工程河堤加固和施工设计提供了参考,该研究方法也可为同类工程提供借鉴。
| [1] |
白永年.
中国堤坝防渗加固新技术[M]. 北京: 中国水利水电出版社, 2001 .
( 0) 0)
|
| [2] |
苏利军.基于极限平衡法和有限元法的土质边坡稳定分析研究[D].成都:西华大学, 2012.
SU Lijun. Study of earth slope stability based on limit equilibrium method & finite element method[D]. Chengdu: Xihua University, 2012. (  0) 0)
|
| [3] |
张炜. 极限平衡法研究现状[J].
科技信息 , 2009 (10) : 64-64 ZHANG Wei. The research status of the limit equilibrium method[J]. Science and Technology Information , 2009 (10) : 64-64 (  0) 0)
|
| [4] |
张宏洋, 杨文海, 陶宗涛, 等. 土质边坡动力稳定数值分析方法评述[J].
南水北调与水利科技 , 2012, 10 (6) : 171-175 ZHANG Hongyang, YANG Wenhai, TAO Zongtao, et al. Review on numerical analysis of dynamic stability of soil slope[J]. South-to-North Water Diversion and Water Science & Technology , 2012, 10 (6) : 171-175 (  0) 0)
|
| [5] |
陈祖煜.
土质边坡稳定分析[M]. 北京: 中国水利水电出版社, 2003 .
( 0) 0)
|
| [6] |
ZIENKIEWICZ O C, HUMPHESON C, LEWIS R W. Associated and non-associated viscous-plasticity and plasticity in soil mechanics[J].
Geotechnique , 1975, 5 (4) : 671-689 ( 0) 0)
|
| [7] |
关立军.基于强度折减的土坡稳定分析方法研究[D].大连:大连理工大学, 2003.
GUAN Lijun. Study of dam slope stability analysis method based on strength reduction[D]. Dalian: Dalian University of Technology, 2003. http://www.oalib.com/references/17062531 (  0) 0)
|
| [8] |
麦麦提明·依比布拉. 基于瑞典法和毕肖普法对比的边坡稳定性[J].
水利科技与经济 , 2015, 21 (6) : 12-14 Yibibula. Slope stability study based on the Swedish method and the Bishop method[J]. Water Conservancy Science and Technology and Economy , 2015, 21 (6) : 12-14 (  0) 0)
|
| [9] |
宋琨, 晏鄂川, 毛伟, 等. 广义Hoek-Brown准则中强度折减系数的确定[J].
岩石力学与工程学报 , 2012, 31 (1) : 106-112 SONG Kun, YAN Echuan, MAO Wei, et al. Determination of shear strength reduction factor for generalized Hoek-Brown Criterion[J]. Chinese Journal of Rock Mechanics and Engineering , 2012, 31 (1) : 106-112 (  0) 0)
|
| [10] |
郑颖人, 赵尚毅, 宋雅坤. 有限元强度折减法研究进展[J].
后勤工程学院学报 , 2005, 21 (3) : 1-6 ZHENG Yingren, ZHAO Shangyi, SONG Yakun. The research advancement of FEM strength reduction method[J]. Journal of Logistical Engineering University , 2005, 21 (3) : 1-6 (  0) 0)
|
| [11] |
郑颖人, 赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J].
岩石力学与工程学报 , 2004, 23 (19) : 3381-3388 ZHENG Yingren, ZHAO Shangyi. Application of strength reduction FEM in soil and rock slope[J]. Chinese Journal of Rock Mechanics and Engineering , 2004, 23 (19) : 3381-3388 (  0) 0)
|
| [12] |
褚雪松, 庞峰, 李亮, 等. 边坡稳定有限元强度折减法与极限平衡法对比[J].
人民黄河 , 2011, 33 (10) : 93-95 CHU Xuesong, PANG Feng, LI Liang, et al. Comparative study on FEM strength reduction method and limit equilibrium method for the slope stability analysis[J]. Yellow River , 2011, 33 (10) : 93-95 (  0) 0)
|
| [13] |
贾超, 张国荣. 基于强度折减法随机裂隙岩体结构稳定性分析[J].
山东大学学报(工学版) , 2013, 43 (6) : 57-64 JIA Chao, ZHANG Guorong. Stability analysis of fandom fractured rock mass structure based on the strength reduction method[J]. Journal of Shandong University(Engineering Science) , 2013, 43 (6) : 57-64 (  0) 0)
|
| [14] |
李广信.
高等土力学[M]. 北京: 清华大学出版社, 2004 .
( 0) 0)
|
| [15] |
栾茂田, 武亚军, 年廷凯. 强度折减有限元法中边坡失稳的塑性区判据及其应用[J].
防灾减灾工程学报 , 2003, 23 (3) : 1-8 LUAN Maotian, WU Yajun, NIAN Yankai. The plastic zone criterion and its application of slope failure in strength reduction finite element method[J]. Journal of Disaster Prevention and Mitigation Engineering , 2003, 23 (3) : 1-8 (  0) 0)
|
| [16] |
GRIFFITHS D V, LANE P A. Slope stability analysis by finite[J].
Geotechnique , 1999, 49 (3) : 387-403 DOI:10.1680/geot.1999.49.3.387 ( 0) 0)
|
| [17] |
曹先锋. 边坡稳定分析的温控参数折减有限元法[J].
岩土工程学报 , 2006, 28 (11) : 2039-2042 CAO Xianfeng. Temperature driving strength reduction method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering , 2006, 28 (11) : 2039-2042 (  0) 0)
|
| [18] |
陈力华, 靳晓光. 有限元强度折减法中边坡三种失效判据的适用性研究[J].
土木工程学报 , 2012, 45 (9) : 136-146 CHEN Lihua, JIN Xiaoguang. Study on the applicability of three criteria for slope instability using finite element strength reduction method[J]. China Civil Engineering Journal , 2012, 45 (9) : 136-146 (  0) 0)
|
| [19] |
裴利剑, 屈本宁, 钱闪光. 有限元强度折减法边坡失稳判据的统一性[J].
岩土力学 , 2010, 31 (10) : 3337-3341 PEI Lijian, QU Benning, QIAN Shanguang. Uniformity of slope instability criteria of strength reduction with FEM[J]. Rock and Soil Mechanics , 2010, 31 (10) : 3337-3341 (  0) 0)
|
| [20] |
陈国庆, 黄润秋, 石豫川, 等. 基于动态和整体强度折减法的边坡稳定性分析[J].
岩石力学与工程学报 , 2014, 33 (2) : 243-256 CHEN Guoqing, HUANG Runqiu, SHI Yuchuan, et al. Stability analysis of slope based on dynamic and whole strength reduction methods[J]. Chinese Journal of Rock Mechanics and Engineering , 2014, 33 (2) : 243-256 (  0) 0)
|
| [21] |
陶煜, 刘卫群. 裂隙岩体渗流-应力耦合等效渗流阻模型[J].
岩土力学 , 2012, 33 (7) : 2041-2047 TAO Yu, LIU Weiqun. An equivalent seepage resistance model with seepage-stress coupling for fractured rock mass[J]. Rock and Soil Mechanics , 2012, 33 (7) : 2041-2047 (  0) 0)
|
| [22] |
杨琛.密集挖孔桩桩孔稳定性分析[D].长沙:中南大学, 2014.
YANG Chen. Analysis on the stability of pile holes in dense hole digging piles[D]. Changsha: Central South University, 2014. (  0) 0)
|
| [23] |
武科, 马秀媛, 尚蕾. 土坝加固效果分析[J].
山东大学学报(工学版) , 2004, 34 (2) : 80-83 WU Ke, MA Xiuyuan, SHANG Lei. An analysis of the solid dam reinforcement[J]. Journal of Shandong University(Engineering Science) , 2004, 34 (2) : 80-83 (  0) 0)
|
| [24] |
王为.基于状态相关性的土体渗透变形特性试验研究[D].长沙:长沙理工大学, 2013.
WANG Wei. Experimental research on seepage failure of soils based on correlations of states[D]. Changsha: Changsha University of Science & Technology, 2013. (  0) 0)
|
| [25] |
刘建钊, 史魏. 复杂地质旋挖组合成桩工艺[J].
施工技术 , 2014 (S1) : 19-22 LIU Jianzhao, SHI Wei. Combined pile forming technology under complex geological conditions[J]. Construction Technology , 2014 (S1) : 19-22 (  0) 0)
|
| [26] |
卢春华. 非金属同径孔壁支护技术[J].
煤田地质与勘探 , 2013, 41 (3) : 87-89 LU Chunhua. Nonmetal and isodiametric sidewall strengthening technology[J]. Coal Geology & Exploration , 2013, 41 (3) : 87-89 (  0) 0)
|




