2. 山东大学电气工程学院, 山东 济南 250061
2. College of Electrical Engineering, Shandong University, Jinan 250061, Shandong, China
均值聚类算法是以每个数据随着经济的不断发展, 城市配电网的规模越来越大, 复杂度越来越高, 对城市配电网进行合理有效的划分, 有利于提高配电网运行的经济性和供电可靠性[1-2]。传统的配电网分区划分方法大部分以行政区作为边界进行划分, 没有考虑配电网的实际运行情况, 从而导致划分方案与实际的网架结构相差太大, 不便于配电网的规划建设。文献[3]采用了自由分区法, 人为干扰因素太多, 对预测方法的选取具有一定的局限性, 通用性有待于进一步提高, 仅仅适用于配电网建设初期网架结构无需大范围调整的地区; 文献[4]提出了一种以各分区负荷最均匀为目标的等负荷分区方法, 该方法虽然方便简单, 但是核心街区的选定自由度太大, 不能体现分区负荷密度的差异和变电站容量的差异; 文献[5]提出了基于改进K-means聚类算法的供电块划分方法, 但是在初始聚类中心的选取过程中没有考虑密度因素, 容易取到噪声点; 文献[6]利用Voronoi图对变电站供电区域进行划分, 但该方法是在假定负荷均匀分布的前提下提出的, 没有考虑负荷分布的不均匀和负荷对可靠性要求的差异; 文献[7]提出了基于广义节点的配电网区域划分方法, 提出将配电网转化成带权的广义节点网络, 从而根据各广义节点的分布关系进行供电区域的划分。
为了进一步提高配电网布局的合理性和供电可靠性, 避免变电站之间不合理的联络, 本研究以聚类算法的思想为基础, 提出了一种基于密度的改进K均值聚类算法, 对配电网进行区块划分, 使大规模的配电网层次清晰, 结构合理, 便于维护和管理[8]。
1 配网区块划分的原则《城市中低压配电网改造技术导则》《配电网规划设计技术实施细则》均对配网分区提出了明确要求:城市中压配电网应该根据变电站的位置、容量, 在满足变电站供电半径的前提下, 将配电网划分为大小合适、相互独立的区块, 区块之间不宜交叉重叠[9-11]。每个供电块的负荷应该相对均衡, 在发生故障时, 有利于负荷的转供, 提高了供电可靠性。除此之外, 还需满足以下原则:
(1)配网区块划分的结果应满足近期负荷发展的需求。划分方案不仅要考虑远景变电站的布点情况, 每个区块的变电站还要留出足够的裕度, 以应对未来负荷快速增长超过预测负荷的情况。
(2)配网区块划分方法应该满足网架规划过程中的经济性和实用性的要求。如果互联变电站相距太远, 会导致后续配电网规划的不合理, 引起投资浪费。
(3)配网区块划分方法需要以相关的理论基础为支撑, 必须对各地区的配电网划分有良好的通用性, 适应于任何地区的配电网规划。
(4)对负荷饱和区和负荷快速发展区, 划分方案中每个区块的接线方式不宜太多, 以一到两组标准接线方式为宜。区块内的变电站或电缆沟出线点应能满足该区块的供电需求, 并预留足够的裕度, 满足未来负荷增长的需求。
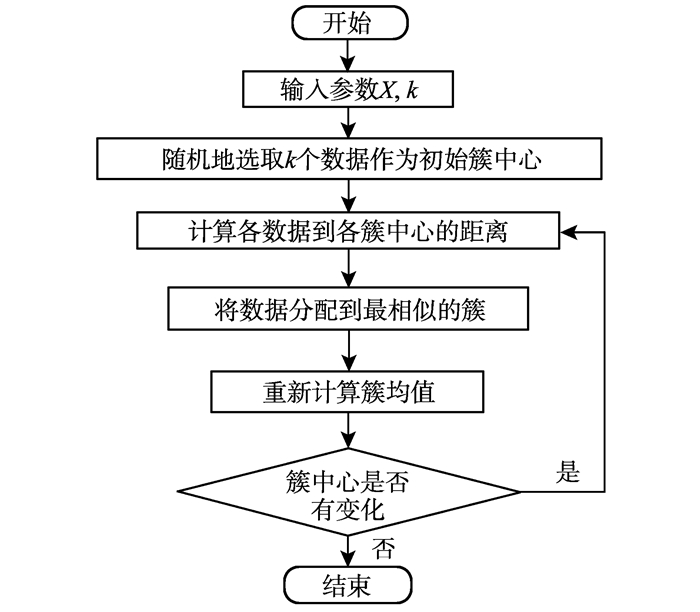
2 基于密度的改进K均值聚类算法 2.1 传统K均值聚类算法传统的K均值聚类算法是以每个数据点到各聚类中心的某种距离之和作为优化的目标函数, 利用函数求极值的方法得到迭代运算的调整规则[12-16]。其计算流程如图 1所示。
|
图 1 K均值聚类算法流程图 Figure 1 Flow chart of K-means clustering algorithm |
传统K均值聚类算法的优点是:(1)对于簇内数据对象密集、簇间数据对象区别明显的数据集, K均值聚类算法的效率较高。(2)在数据挖掘中, 该算法与DBSCAN(density-based spatial clustering of applications with noise, 具有噪声的基于密度的空间聚类应用)算法相比, 效率更高。
但该算法也存在明显的缺点:(1)K均值聚类算法的聚类数K需要事先给定, 不同的K可能导致不同的聚类结果, 难以达到预期的聚类效果。(2)K均值聚类算法随机选取初始聚类中心, 如果初始聚类中心选择不合理, 可能无法得到有效的聚类结果, 这也是传统K均值聚类算法存在的主要缺陷。
2.2 K均值聚类算法的改进针对传统的K均值聚类算法的缺点与不足, 本文从初始聚类中心的选取和最佳聚类数K的确定两方面进行了改进。
2.2.1 初始聚类中心的选取传统K均值聚类算法以随机方式选取初始聚类中心, 这种处理方式往往对聚类结果影响较大, 如果只按照距离最远的原则进行选取, 很容易取到噪声点, 影响聚类效果。所以在选取初始聚类中心时, 需要综合考虑数据对象之间的距离和数据对象的密度两个方面的因素。在一个数据集合里, 从处于高密度区域的数据对象中选择距离最远的K个对象作为初始聚类中心, 能够避免噪声点的干扰。
为便于描述, 将以某一数据对象为圆心, 以某一预定值r为半径的圆形区域定义为该数据对象的r-邻域。根据聚类经验, r通常取所有数据对象之间平均距离的一半。
设定一个阈值P, 如果一个数据对象的r-邻域内至少含有P个对象, 那么称该对象为核心对象。两个n维数据对象之间的欧氏距离
| $ d\left( {i,j} \right) = \sqrt {{{\left( {{x_{i1}} - {y_{i1}}} \right)}^2} + {{\left( {{x_{i2}} - {y_{i2}}} \right)}^2} + \cdots + {{\left( {{x_{in}} - {y_{in}}} \right)}^2}} , $ | (1) |
式中:d(i, j)是n维数据对象i和j的距离; xi1, xi2, …, xin和yi1, yi2, …, yin分别表示对象i和对象j在第1, 2, …, n维的数据。
该算法首先计算所有数据对象之间的欧氏距离d(i, j), 然后计算每个数据对象xi的r-邻域内包含的数据对象的个数, 如果数据对象的个数大于阈值P, 就将该数据对象加入到高密度集合D中, 最后从集合D中找出相互距离最远的K个数据对象作为初始聚类中心, 运用传统的K均值聚类算法进行聚类。具体的流程如图 2所示。

|
图 2 初始聚类中心的选取流程图 Figure 2 Flow chart of the initial clustering center selection |
为了评价聚类结果是否满足类内相聚和类间分离这一条件, 本研究提出了一种更有效的评价方式, 即利用类内差异度和类间差异度构建评价函数评价聚类的有效性。
假设给定一组数据集X={x1, x2, …, xN}, 要求将这个数据集分为k个簇(C1, C2, …, Ck), 最终每一簇的聚类中心分别为(m1, m2, …, mk)。
类内差异度用来衡量聚类的紧凑性, 用类内各数据对象到其所属类的聚类中心距离的平均值表示,其定义为
| $ D{\rm{in = }}\frac{{\sum\limits_{i = 1,j = 1}^{i = k,j = N} {\sqrt {{{\left( {{x_j} - {m_i}} \right)}^2}} } }}{N}, $ | (2) |
类间差异度用来衡量不同聚类之间的分离程度, 用聚类中心之间距离的最小值来表示, 其定义为
| $ {D_{{\rm{out}}}} = \mathop {\min }\limits_{2 \le k \le {k_{\max }}} d\left( {{m_i},{m_j}} \right), $ | (3) |
式中:N为数据对象的个数; mi为类cj的聚类中心; xj为类cj中的数据对象; d(mi, mj)为类ci与类cj之间的欧几里得距离。
本研究以Din、Dout为基础, 提出了新的聚类有效性评价函数
| $ V\left( k \right) = \frac{{{D_{{\rm{out}}}} - {D_{{\rm{in}}}}}}{{{D_{{\rm{out}}}} + {D_{{\rm{in}}}}}} $ | (4) |
由评价函数可知, 函数的取值范围是[-1, 1], V(k)越接近1, 说明数据对象的类内差异度相对于类间差异度可以忽略, 聚类效果越好; V(k)越接近-1, 说明数据对象的类间差异度相对于类内差异度可以忽略, 聚类效果越差。为了使类内尽量相聚, 类间尽量分离; V(k)最大时, 聚类结果最优, 对应的k即为最佳聚类数目K。
3 配网区块划分方法 3.1 形成配网区块初始聚类中心配网区块初始聚类中心的选择实际上就是在被划分的供电范围内选择K个核心变电站或电缆沟的出线点, 然后运用传统的K均值聚类算法对供电片区进行划分, 为配电网的规划和接线方式的选择提供方便, 便于配电网的管理和维护[17-20]。
具体选择步骤为:(1)计算规划区域所有变电站或电缆沟出线点之间的距离d(i, j)。(2)计算每个变电站的r-邻域内包含的变电站的个数, 如果变电站的个数大于阈值P, 就将该变电站加入高密度区域集合D中。(3)从集合D中取出处于最高密度区域的变电站a1, 即该变电站的半径为r的邻域内包含的变电站个数最多, 然后从集合D中删除该变电站, 将a1加入到初始聚类中心集合。(4)计算a1和集合D中所有变电站的距离, 找出离a1最远的变电站a2, 从集合D中删除该变电站, 然后将a2加入初始聚类中心集合。(5)从集合D中找出离a1和a2最远的变电站a3, 即得到的a3与a1、a2的距离之和最大, 从集合D中删除该变电站, 然后将a3加入到初始聚类中心集合。(6)重复步骤(5), 直到选出K个变电站作为初始聚类中心。(7)如果得到的聚类数小于最佳聚类数K, 则动态缩小阈值P, 重新选取高密度的最佳聚类中心。(8)选出K个处于高密度区域的初始聚类中心后, 运用K均值聚类算法进行供电块的划分。
为满足中压配电网中变电站供电半径的要求, 根据聚类经验, 半径r取所有变电站之间平均距离的一半, 阈值P的初值为4。
3.2 确定最佳区块划分数K为了解决基于密度的改进K均值聚类算法中最佳聚类数K的选择问题, 结合V(k), 将聚类数k在[kmin, kmax]内遍历, 然后运用基于密度的改进K均值聚类算法进行聚类, 得到不同聚类数k对应的聚类结果。然后用V(k)评价多次聚类结果的质量, 最后找出V(k)的最大值对应的聚类数k, 即为最佳聚类数K。
最佳网格划分数K确定的具体流程为:(1)运用基于密度的改进K均值聚类算法将变电站聚为k类, 得到聚类后的中心M={m1, m2, …, mk}; (2)求出每个变电站xj处的Din; (3)利用得到的聚类中心M={m1, m2, …, mk}, 求出聚类数k对应的Dout; (4)求出每个k所对应的V(k), 选择V(k)的最大值所对应的k作为最佳聚类数K。
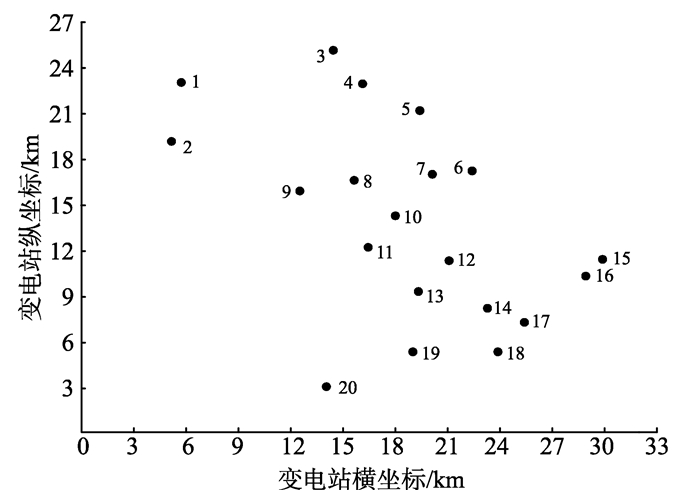
4 算例分析某城市规划建设20座10 kV变电站, 变电站的位置分布如图 3所示。
|
图 3 某城市10 kV变电站位置分布图 Figure 3 The location of 10 kV substations in a city |
以左下角为原点建立平面直角坐标系, 得到每个变电站的位置坐标, 如表 1所示。
| 表 1 某城市10 kV变电站坐标统计表 Table 1 Statistics of coordinates for 10 kV substations in a city |
根据本文提出的基于密度的改进K均值聚类算法进行供电块划分, 供电块划分数k的取值范围是2~9, 得到不同的划分方案结果如表 2所示。
| 表 2 不同划分方案和V(k)计算结果 Table 2 Different partitioning schemes and the calculation results of V(k) |
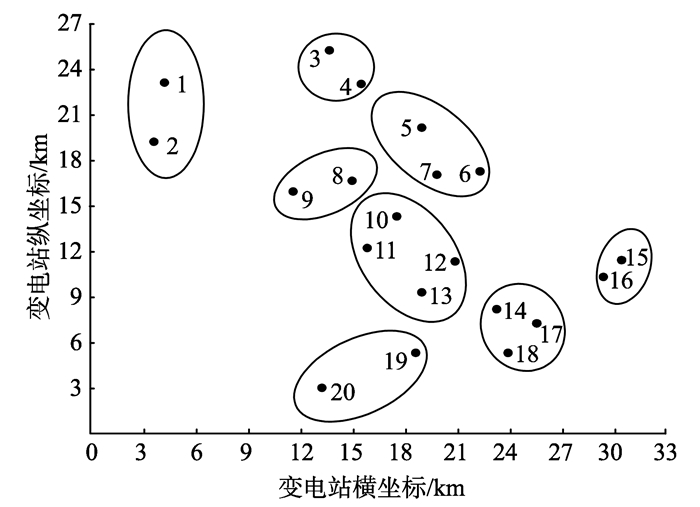
从表 2可以看出, 划分数为8的V(k)值远大于其他划分方案, 因此, 该区域供电块划分数为8时的划分方案为最佳划分方案, 供电块的最终划分方案如图 4所示。
|
图 4 某城市配网区块最佳划分方案示意图 Figure 4 Diagram of optimal partitioning schemes fordistribution network in a city |
传统的K均值聚类算法需要随机选取初始聚类中心, 而且聚类结果对初始聚类中心的依赖性很强, 同时还需要预先指定聚类数目。为了便于比较, 运用本文提出的聚类有效性评价函数对改进前后的两种聚类算法进行评价, 得到图 5所示的折线图。

|
图 5 改进前后聚类评价函数折线图 Figure 5 Curve of clustering evaluation function before and after improvement |
从图 5所示评价函数折线图可以看出, 改进前聚类算法的评价函数值总体上低于改进后的评价函数值, 而且聚类结果受初始聚类中心的影响, 随机性较强, 而改进后的聚类算法的评价函数值呈现先增后减的趋势, 在k=8时达到最大值, 聚类结果最优。
将不同时期规划建设的变电站与已建成变电站同时作为数据对象, 进行配网区块的划分, 能够使划分方案满足不同时期的负荷发展需求。另外, 改进后聚类算法的评价函数能够体现类内相聚、类间分离的要求, 避免相距太远的变电站之间相互联络, 提高了配电网运行的经济性和实用性。
对城市配电网进行供电区块划分的目的之一是实现负荷的均衡, 根据配电网的实际发展情况, 变电站越密集的区域, 负荷密度越高。运用本文提出的改进K均值聚类算法, 能够将距离相近的变电站聚为一类, 选择合适的配电网接线方式, 将类内变电站联络在一起, 便于负荷的转供, 实现负荷的均衡发展。
通过以上分析得出, 运用改进后的K均值聚类算法进行配网区块划分, 能够满足配网区块划分的原则, 并且在性能上较传统的K均值聚类算法有所改善。
5 结论(1)初始聚类中心的选取同时考虑了变电站的距离和密度两个方面的约束, 使聚类结果更加合理有效, 避免了随机选取初始聚类中心造成的聚类结果的不确定性;
(2)新的聚类评价函数通过有效性评价指标确定了配网区块的划分数量, 满足类内相聚、类间分离的划分原则, 建立起全局最优的供电区块划分方案, 在满足配电网运行经济性的前提下, 实现了负荷的均衡, 从而提高了配电网的供电可靠性。
| [1] |
肖峻, 崔艳妍, 王建民, 等. 配电网规划的综合评价指标体系与方法[J].
电力系统自动化 , 2008, 32 (15) : 36-40 XIAO Jun, CUI Yanyan, WANG Jianmin, et al. A hierarchical performance assessment method on the distribution network planning[J]. Automation of Electric Power Systems , 2008, 32 (15) : 36-40 (  0) 0)
|
| [2] |
霍凯龙, 王主丁, 畅刚, 等. 目标年中压配电网规划实用方法[J].
电网技术 , 2013, 37 (6) : 1769-1774 HUO Kailong, WANG Zhuding, CHANG Gang, et al. A practical method for medium voltage distribution network planning in target year[J]. Power System Technology , 2013, 37 (6) : 1769-1774 (  0) 0)
|
| [3] |
李智宇, 陈建福, 张尧. 基于优化分区的配电网规划研究及实践[J].
广西电力 , 2006 (4) : 1-4 LI Zhiyu, CHEN Jianfu, ZHANG Yao. Study and practice about distribution network planning based on optimal partitioning[J]. Guangxi Electric Power , 2006 (4) : 1-4 (  0) 0)
|
| [4] |
宋蒙, 刘健, 刘巩权. 基于优化分区的城市配电网架规划[J].
继电器 , 2005, 33 (23) : 31-35 SONG Meng, LIU Jian, LIU Gongquan. Urban distribution network planning based on optmial partitioning[J]. Reiay , 2005, 33 (23) : 31-35 (  0) 0)
|
| [5] |
韩俊, 谈健, 黄河, 等. 基于改进K-means聚类算法的供电块划分方法[J].
电力自动化设备 , 2015, 35 (6) : 123-129 HAN Jun, TAN Jian, HUANG He, et al. Power-supplying block partition based on improved K-means clustering algorithm[J]. Electric Power Automation Equipment , 2015, 35 (6) : 123-129 (  0) 0)
|
| [6] |
杨丽徙, 王金凤, 王家耀. 基于Voronoi图的配电变压器定位和供电区域划分[J].
测绘通报 , 2004 (5) : 33-35 YANG Lixi, WANG Jinfeng, WANG Jiayao. Locating of distribution transformers and power supply area plotting based on Voronoi diagrams[J]. Bulletin of Surveying and Mapping , 2004 (5) : 33-35 (  0) 0)
|
| [7] |
张新昌, 张项安, 刘星. 基于广义节点的配电网区域控制划分[J].
电力系统保护与控制 , 2014, 42 (7) : 122-127 ZHANG Xinchang, ZHANG Xiangan, LIU Xing. Partition operation on distribution network based on theory of generalized node[J]. Power System Protection and Control , 2014, 42 (7) : 122-127 (  0) 0)
|
| [8] |
葛少云, 韩俊, 刘洪, 等. 基于供电能力的主变站间联络结构优化[J].
电网技术 , 2012, 36 (8) : 129-135 GE Shaoyun, HAN Jun, LIU Hong, et al. Optimization of contact structure among main transformer stations in regional power network based on power supply capability[J]. Power System Technology , 2012, 36 (8) : 129-135 (  0) 0)
|
| [9] |
葛少云, 贾鸥莎. 配电变电站多阶段优化规划模型[J].
电网技术 , 2012, 36 (10) : 113-118 GE Shaoyun, JIA Ousha. Multi-stage model for optimal distribution substation planning[J]. Power System Technology , 2012, 36 (10) : 113-118 (  0) 0)
|
| [10] |
王玉瑾, 王主丁, 张宗益, 等. 基于初始站址冗余网格动态减少的变电站规划[J].
电力系统自动化 , 2010, 34 (12) : 39-43 WANG Yujin, WANG Zhuding, ZHANG Zongyi, et al. Substation planning based on initial substation site decrease in redundant meshes[J]. Automation of Electric Power Systems , 2010, 34 (12) : 39-43 (  0) 0)
|
| [11] |
彭文, 杜晓东, 石敏. 基于负荷区域划分的配电变电站规划模型[J].
电力自动化设备 , 2015, 33 (1) : 112-117 PENG Wen, DU Xiaodong, SHI Min. Distribution substation planning model based on load region division[J]. Electric Power Automation Equipment , 2015, 33 (1) : 112-117 (  0) 0)
|
| [12] |
傅德胜, 周辰. 基于密度的改进K均值算法及实现[J].
计算机应用 , 2011, 31 (2) : 432-434 FU Desheng, ZHOU Chen. Improved K-means algorithm and its implementation based on density[J]. Journal of Computer Applications , 2011, 31 (2) : 432-434 DOI:10.3724/SP.J.1087.2011.00432 (  0) 0)
|
| [13] |
JOSHI K D, NALWADE P S. Modified K-means for better initial centers[J].
International Journal of Computer Science and Mobile Computing , 2013, 2 (7) : 219-223 ( 0) 0)
|
| [14] |
SEYED Mahdi Mazhari.A new method for simultaneous determination of distribution substation optimal service areas and capacities using modified membership matrix [C]//International Conference on Environment and Electrical Engineering. Venice, Italy:IEEE Press, 2012:637-642.
( 0) 0)
|
| [15] |
MA G W, XU Z H, ZHANG W, et al. An enriched K-means clustering method for grouping fractures with meliorated initial centers[J].
Arabian Journal of Geosciences , 2014 : 1-13 ( 0) 0)
|
| [16] |
徐平安, 唐雁, 石教开, 等. 基于薛定谔方程的K-means聚类算法[J].
山东大学学报(工学版) , 2015, 45 (6) : 1-8 XU Pingan, TANG Yan, SHI Jiaokai, et al. K-means clustering algorithm based on the Schrodinger equation[J]. Journal of Shandong University(Engineering Science) , 2015, 45 (6) : 1-8 (  0) 0)
|
| [17] |
唐小波, 刘笠, 张娟. 基于自适应权重Voronoi图的配电网供电分区方法[J].
电力系统保护与控制 , 2015, 43 (19) : 83-88 TANG Xiaobo, LIU Li, ZHANG Juan. Method of power distribution network partition based on adaptive weighted Voronoi diagram[J]. Power System Protection and Control , 2015, 43 (19) : 83-88 (  0) 0)
|
| [18] |
屈刚, 程浩忠, 马则良, 等. 考虑联络线传输功率的双层分区多目标输电网规划[J].
中国电机工程学报 , 2009, 29 (31) : 40-46 QU Gang, CHENG Haozhong, MA Zeliang, et al. Bi-level multi-objective transmission planning with consideration of tie-line power transfer capability[J]. Proceedings of the CSEE , 2009, 29 (31) : 40-46 (  0) 0)
|
| [19] |
张欣, 高卫国, 苏运. 基于函数型数据分析和K-means算法的电力用户分类[J].
电网技术 , 2015, 39 (11) : 3153-3162 ZHANG Xin, GAO Weiguo, SU Yun. Electricity consumer archetypes study based on functional data analysis and K-means algorithm[J]. Power System Technology , 2015, 39 (11) : 3153-3162 (  0) 0)
|
| [20] |
张新猛, 蒋盛益. 一种基于相似度概率的不确定分类数据聚类算法[J].
山东大学学报(工学版) , 2011, 41 (3) : 12-16 ZHANG Xinmeng, JIANG Shengyi. An algorithm for clustering uncertain categorical data based on similarity probability[J]. Journal of Shandong university(Engineering Science) , 2011, 41 (3) : 12-16 (  0) 0)
|




