对传统的手眼机器人系统, 获取摄像机坐标系与机器人末端执行器之间的相对位置关系是非常必要的。这种相对位置关系不可测量, 需要使用相应的算法求解, 求解的过程称为手眼标定[1]。目前, 手眼标定问题已得到了广泛的研究。文献[2]提出了一种高效的线性算法求解手眼标定问题, 并且指出最少需要2个具有非平行旋转坐标轴的旋转运动才可以完成求解。文献[3]提出了一种采用四元数来表示旋转的算法, 并且给出了一个基于SVD的线性解决方案。文献[4]基于四元数的最小二乘法, 对手眼标定提出了一种八维空间的求解方法。文献[5]利用螺旋运动理论分析手眼标定, 提出了手眼几何的约束条件。基于文献[5]的工作, 文献[6]提出了一种基于对偶四元数的手眼标定算法, 该算法结合SVD算法可以同时求解旋转和平移参数。文献[7]提出了一种基于螺旋运动的算法, 并推导出了与文献[6]相似的求解方程。考虑到随机噪声的影响, 许多研究人员都会在手眼标定算法中引入最优化方法。文献[8]对旋转和平移参数的求解都采用非线性优化, 使用与弗罗贝尼乌斯范数相似的代价函数进行优化。文献[9]也提出了一种相似的优化策略。文献[10]在手眼标定中引入了正则坐标系, 简化了优化参数的特征描述。文献[11]对采用四元数的旋转参数进行了非线性优化, 同时也介绍了在非线性优化中同时求解机器人-世界和手-眼的位置关系的方法[12]。文献[13]针对手眼标定提出了一种基于新的SE(3)度量的非线性优化算法, 该新度量有自动最优化权重的能力。虽然以上研究工作取得了很好的结果, 但是涉及的优化过程都是局部优化, 可能由于迭代初值选取不当而陷入局部最小化陷阱。为此文献[14]提出了一种基于凸优化的手眼标定算法, 该算法是一种全局优化算法, 不会陷入局部最小值陷阱, 但优化过程需要较多的迭代步数, 运算复杂度较大。本文提出了一种无需迭代计算和初始值估计的非最小优化的方法。与其它使用局部、全局优化的方法相比, 这种方法计算复杂度低, 运算时间短, 并表现出了较高的精确性和可靠性。
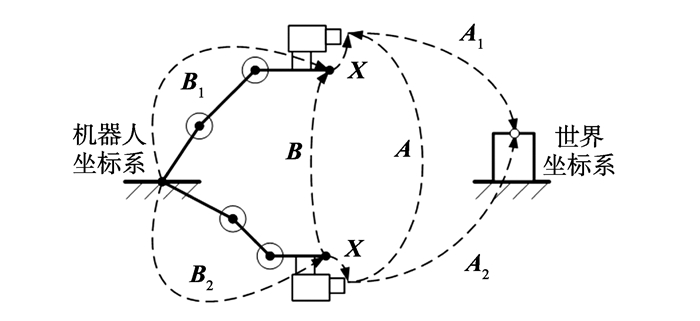
1 手眼标定问题描述手眼标定问题通常使用齐次矩阵来描述, 如图 1所示, Ai(i=1, 2)表示从摄像机坐标系到世界坐标系的第i个相对位置关系矩阵, Bi(i=1, 2)表示从机器人基坐标到末端执行器坐标系的第i个姿势矩阵, X表示机器人末端执行器到摄像机坐标系的相对位置关系矩阵, 可以得到
| ${\boldsymbol{A}_1}\boldsymbol{X}{\boldsymbol{B}_1} = {\boldsymbol{A}_2}\boldsymbol{X}{\boldsymbol{B}_2}。$ | (1) |
|
图 1 手眼标定方程AX=XB Figure 1 Hand-eye calibration by solving AX=XB |
在式(1)的两边分别乘以A1-1和B2-1, 可以得到
| $\boldsymbol{A}_1^{ - 1}{\boldsymbol{A}_2}\boldsymbol{X} = \boldsymbol{X}{\boldsymbol{B}_1}\boldsymbol{B}_2^{ - 1}。$ | (2) |
式(2)即为文献[1]首先提出的著名的手眼标定方程
| $\boldsymbol{AX} = \boldsymbol{XB},$ | (3) |
式中:X为手眼标定参数矩阵, 在立体视觉的机器人系统中, X表示机器人末端执行器到基准摄像机坐标系的相对位置关系; A=A2A1-1, B=B2-1B1。方程里每个矩阵都是齐次的, 其形式为:
| $D = \left[{\begin{array}{*{20}{c}} {{\boldsymbol{R}_D}}&{{\boldsymbol{t}_D}} \\ {{0^{\text{T}}}}&1 \end{array}} \right],$ |
式中:矩阵RD和tD分别表示齐次矩阵D的旋转矩阵和平移矢量。因此, 公式(3)也可以写作
| $\boldsymbol{{R_A}{R_X} = {R_X}{R_B}},$ | (4) |
| $\boldsymbol{{R_A}{t_X} + {t_X} = {R_X}{t_B} + {t_X}}。$ | (5) |
之前的手眼标定算法[8-13]全都使用了局部最优化方法, 如Levenberg-Marquardt算法等。目标函数格式通常为:
| $J = \sum\limits_{i = 1}^N {\left( {{{\left\| {{\boldsymbol{r}_i}} \right\|}^2} + \lambda {{\left\| {{\boldsymbol{t}_i}} \right\|}^2}} \right)} ,$ |
式中: ri是旋转参数误差项矩阵; ti是平移参数误差项矩阵; N为误差项的个数; λ是权重系数;‖·‖是欧氏距离的度量。在计算机视觉理论中, 将式(4)中的平方和函数最小化是一个比较繁琐的非凸优化过程[15-18], 通常有多个极小值, 往往会陷入局部最小值陷阱。这也是以式(4)为目标函数的非线性优化过程需要事先给出一个合适的初始值的原因。平方和目标函数实际上是一种L2-范数误差公式。对于L2-范数目标函数的最小化, 大多数的手眼标定算法(无论局部还是全局优化)都是以非线性捆绑调整的方式来执行的, 这种方法非常耗费运算时间。文献[19]提出了基于非最小化的统计优化理论, 并证明其性能优于最小化优化。非最小化优化理论主要通过构造线性矩阵方程而诱导出相应的代价函数, 通过代价函数推导出特征估计矩阵, 根据特征计算结果得到优化计算的估计值。受到文献[19]的启发, 本文在手眼标定中引入了基于非最小化优化理论。
2 基于非最小化优化的手眼标定首先, 引入张量积运算符⊗和列向量运算符vec[20]。如果M是一个m×n矩阵, P是一个p×o矩阵, M⊗P的张量积定义为[21]:
| $\boldsymbol{M} \otimes \boldsymbol{P} = \left[{\begin{array}{*{20}{c}} {{\boldsymbol{M}_{11}}\boldsymbol{P}}& \cdots &{{\boldsymbol{M}_{1n}}\boldsymbol{P}} \\ \vdots & \ddots & \vdots \\ {{\boldsymbol{M}_{m1}}}& \cdots &{{\boldsymbol{M}_{mn}}\boldsymbol{P}} \end{array}} \right],$ | (6) |
列向量运算符定义为:
| ${\text{vec}}\left( M \right) = {\left[{{M_{11}},\cdots ,{M_{1n}},\cdots ,{M_{21}},\cdots ,{M_{mn}}} \right]^{\text{T}}}。$ | (7) |
根据式(6)和(7), 可以将公式(4)和(5)改写为
| $\left[{\begin{array}{*{20}{c}} {{\boldsymbol{I}_9} - {\boldsymbol{R}_{{A_i}}} \otimes {\boldsymbol{R}_{{B_i}}}}&{{0_{9 \times 3}}} \\ {{\boldsymbol{I}_3} \otimes \boldsymbol{t}_{{B_i}}^{\text{T}}}&{{\boldsymbol{I}_3} - {\boldsymbol{R}_{{A_i}}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{\text{vec}}\left( {{\boldsymbol{R}_{\text{X}}}} \right)} \\ {{\boldsymbol{t}_{\text{X}}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{0_{9 \times 1}}} \\ {{\boldsymbol{t}_{{A_i}}}} \end{array}} \right],$ |
假定
| ${\boldsymbol{C}_i}\boldsymbol{x} = {\boldsymbol{d}_i},$ | (8) |
式(8)是一个线性函数, 可以转换成
| $\left[{{\boldsymbol{C}_i}\;\; - {\boldsymbol{d}_i}} \right]\left[{\begin{array}{*{20}{c}} \boldsymbol{x} \\ 1 \end{array}} \right] = {0_{12 \times 1}},$ | (9) |
将所有式(9)排列起来, 可以得到
| $\underbrace {\left[{\begin{array}{*{20}{c}} {{\boldsymbol{C}_1}}&{ - {\boldsymbol{d}_1}} \\ \vdots & \vdots \\ {{\boldsymbol{C}_N}}&{ - {\boldsymbol{d}_N}} \end{array}} \right]}_U\underbrace {\left[{\begin{array}{*{20}{c}} \boldsymbol{x} \\ 1 \end{array}} \right]}_y = {0_{12N \times 1}},$ | (10) |
根据式(10), 可以构造非最小化优化的代价函数
| $\begin{gathered} J\left( \boldsymbol{y} \right) = \frac{1}{{12N}}\sum\limits_{i = 1}^{12N} {{{\left\| {{\boldsymbol{u}_i}\boldsymbol{y}} \right\|}^2} = \frac{1}{{12N}}\sum\limits_{i = 1}^{12N} {{\boldsymbol{y}^{\text{T}}}\boldsymbol{u}_i^{\text{T}}{\boldsymbol{u}_i}\boldsymbol{y} = } } \\ {\boldsymbol{y}^{\text{T}}}\underbrace {\left( {\frac{1}{{12N}}\sum\limits_{i = 1}^{12N} {\boldsymbol{u}_i^{\text{T}}{\boldsymbol{u}_i}} } \right)\boldsymbol{y}}_V = \boldsymbol{y} \cdot \boldsymbol{Vy},\\ \end{gathered} $ |
其中, ui是矩阵U的第i行。为了使J→0, 可以写出其估计方程[16]
| $\boldsymbol{Vy = \lambda y}。$ | (11) |
由于U的噪声干扰, 矩阵V的秩一般大于12, 矩阵V的最小特征值λ对应的特征向量y可以看作是代价函数J的非最小化最优解。得到的向量y的估计值
| $\boldsymbol{\hat y} \propto = \left[{\begin{array}{*{20}{c}} \boldsymbol{x} \\ 1 \end{array}} \right].$ | (12) |
尝试通过使用定性的扰动分析对估计方程(11)进行误差分析, 有
| ${\boldsymbol{V}_{\text{e}}}{\boldsymbol{y}_{\text{e}}} = {\lambda _{\text{e}}}{\boldsymbol{y}_{\text{e}}},$ |
其中:Ve=V+ΔV, 由系数矩阵V和噪声扰动矩阵ΔV组成;同理有ye=y+Δy和λe=λ+Δλ。得到
| $\left( {\boldsymbol{V} + {\Delta _\boldsymbol{v}}} \right)\left( {\boldsymbol{y} + {\Delta _\boldsymbol{y}}} \right) = \left( {\lambda + {\Delta _\lambda }} \right)\left( {\boldsymbol{y} + {\Delta _\boldsymbol{y}}} \right).$ | (13) |
在高斯白噪声而无其它噪声情况下(λ=0), 式(13)的一阶等式可以表示为
| $\boldsymbol{V{\Delta _y} + {\Delta _V}y = {\Delta _\lambda }y},$ | (14) |
将等式(14)两边分别关于y做内积, 得到
| $\boldsymbol{y \cdot V{\Delta _y} + y \cdot {\Delta _V}y = y \cdot {\Delta _\lambda }y},$ | (15) |
由于ui·y=0, y·VΔy以及y·ΔVy都为0。根据式(15), 得到
| $\boldsymbol{{\Delta _y} = - {V^ + }{\Delta _V}y},$ |
其中,V+V=I-yyT, 显然E{Δy}=0。由上面的扰动分析可知, 数据扰动对本文提出的算法影响很小, 并且随着机器人运动次数的增多而变得可以忽略不计。
4 运动选择由等式(11)可知, 如果给优化误差预定义一个阈值, 那么标定运动数据的选择将非常容易实现。运动选择算法[22]如下:
算法1:
给定:运动数据集合C={Ci, i=1, 2, …}、d={di, i=1, 2, …}以及阈值e。
对于第i个运动,
构造
由U(i)计算V(i);
解出V(i)的最小特征值λ(i)和对应特征向量
如果λ(i)>e, 则从C, d和U(i)中删除第i个运动;
直至λ(i)≤e;
本研究所述运动选择的算法具有直接的几何和代数意义, 所以很容易理解和实现。
5 试验分别使用仿真数据和实际数据进行试验以测试本研究提出的手眼标定方法, 并与3种已有方法进行比较。第一种方法是由文献[11]提出的方法。该方法使用了迭代非线性最小化算法, 需要适当的初始值, 为此使用文献[6]的方法估计初始值。第二种方法是由文献[8]提出的单级迭代算法。第三种方法是由文献[14]提出的基于凸优化的方法。在下面的试验和图表中, 本研究的方法将标注为“Ours”, 其他3种方法分别标注为“HDD”, “ZS”, “ZCP”。
5.1 仿真试验在已知手眼关系(Rx, tx)的情况下, 人工生成一系列的机器人手眼运动数据, 并在这些运动数据中添加标准差为σ的高斯噪声。在0~0.1调整σ的取值, 每个取值下所有手眼标定方法都运行100次, 并输出手眼参数的估计矩阵
| $\begin{gathered} {e_{\text{R}}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left\| {{\boldsymbol{R}_{\text{X}}} - {{\boldsymbol{\hat R}}_{\text{X}}}} \right\|}^2}} } ,\hfill \\ {e_{\text{t}}} = \frac{{\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left\| {{\boldsymbol{t}_{\text{X}}} - {{\boldsymbol{\hat t}}_{\text{X}}}} \right\|}^2}} } }}{{{{\left\| {{\boldsymbol{t}_{\text{X}}}} \right\|}^2}}}。 \hfill \\ \end{gathered} $ |
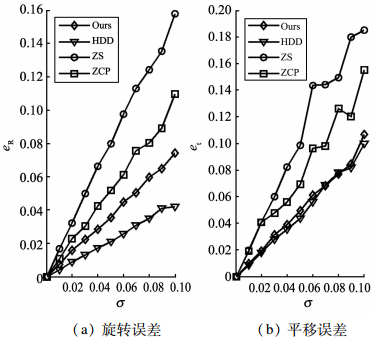
本研究的算法在不同噪声等级下与HDD、ZS、ZCP 3种方法进行了比较, 如图 2所示。
|
图 2 不同噪声等级下各算法误差 Figure 2 Errors in all algorithms with variation in noise level |
由图 2可知:尽管HDD方法在旋转和平移方面误差更小, 但是考虑到HDD方法对初始值的依赖性, 在初始值不合适情况下, HDD方法不会取得较好的优化结果。出于同样的原因, ZS算法效果最差。本文提出的方法性能较好, 优于ZCP方法和ZS算法, 这主要是由于估计方程(14)中的矩阵V减弱了噪声的影响。
仿真试验使用MATLAB V7.8编写所有的算法。计算机系统配置如下:Intel core-i5 CPU 2.90 GHz, 4 G RAM。表 1记录了所有算法运行1 000遍的时间。从表 1可以看出, 本研究的算法用时约为ZS/HDD方法时间的1/10, 不到ZCP方法用时的1/3。试验结果表明, 本研究的算法用时大大小于其他3种算法。在充分考虑误差和时间两方面性能的情况下, 本研究的算法可以作为手眼标定方法的最好选择。
| 表 1 各算法运行时间 Table 1 The running time of all algorithms |
在实际试验中, 使用了一个末端装有2个CCD摄像机的MOTOMAN HP3机器人(如图 3所示)。通过机器人姿态的改变, 摄像机相对标定物移动了16个不同的位置, 在每一个位置通过摄像机记录下标定物图像, 根据每幅图像提取出标定物的特征点集合, 由每幅图像的特征点集合计算出摄像机坐标系到世界坐标系的一个齐次相对位置关系。从第二幅图像开始, 每一幅图像对应的齐次相对位置关系与其前一幅图像对应的齐次关系的逆矩阵相乘, 计算出15个摄像机的运动数据Ai(i=1, …, 15), 这样计算可以有效地避免数据的误差传递。与摄像机的15个运动齐次矩阵相对应, 从机器人控制器里读取机器人末端执行器的15个运动齐次矩阵Bi(i=1, …, 15)。根据摄像机和机器人1~8次的运动数据, 可以运用4种手眼标定算法, 得到机器人系统的手眼关系矩阵X。然后, 根据机器人运动数据Bi(i=9, …, 15)来估计摄像机的运动
| ${{\boldsymbol{\hat A}}_i} = \boldsymbol{X}{\boldsymbol{B}_i}{\boldsymbol{X}^{ - 1}},i = 9,\cdots ,15.$ |

|
图 3 手眼机器人系统 Figure 3 Hand-eye robot system |
比较
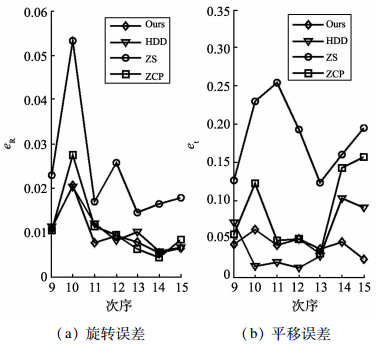
|
图 4 真实试验误差结果 Figure 4 Error results in the real experiments |
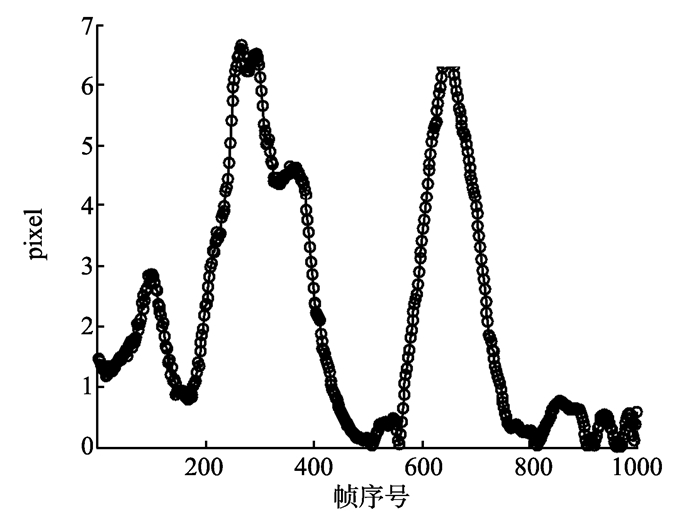
鉴于非最小化优化手眼标定算法在试验中表现出的优越性能, 将其应用到ViKY手术机器人系统(见图 5)的手眼标定中。ViKY是一种腹腔镜手术机器人, 在其末端装有奥林巴斯内窥镜, 并且可以通过内窥镜跟踪手术工具的位置(视觉跟踪/伺服)。利用非最小化优化计算出的手眼标定结果, ViKY机器人进行3 min的视觉伺服操作。计算了每一帧图像的跟踪误差, 第1~1 000帧的误差结果如图 6所示。从图 6中可以看到, 视觉跟踪的误差曲线大致符合阻尼振荡过程, 这表示伺服过程有很好的鲁棒性, 因此该手眼标定方法适用于实际机器人系统的标定。

|
图 5 ViKY手术机器人系统 Figure 5 ViKY surgical robot system |
|
图 6 第1~1 000帧的误差结果 Figure 6 Error-results in the frame from the first to the thousandth |
本研究提出了一种基于非最小化优化的手眼标定方法。与其它算法不同的是, 该算法使用了特征计算而非L2-范数优化, 并采用估计方程实现手眼方程的求解。这种算法不是迭代优化的, 不需要初始值, 所以与其他算法相比, 计算起来更简单。试验结果表明:这种算法具有较强的鲁棒性和有效性。综合考虑标定的误差和运行时间, 这种方法在实际应用中具有明显的优越性, 适合于各种机器人系统的标定, 特别是医学机器人的标定。
| [1] |
SHIU Y C, AHMAD S. Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX=XB[J].
IEEE Transactions on Robotics and Automation , 1989, 5 (1) : 16-29 DOI:10.1109/70.88014 ( 0) 0)
|
| [2] |
TSAI R Y, LENZ R K. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration[J].
IEEE Transactions on Robotics and Automation , 1989, 5 (3) : 345-358 DOI:10.1109/70.34770 ( 0) 0)
|
| [3] |
CHOU J C K, KAMEL M. Finding the position and orientation of a sensor on a robot manipulator using quaternions[J].
The International Journal of Robotics Research , 1991, 10 (3) : 240-254 DOI:10.1177/027836499101000305 ( 0) 0)
|
| [4] |
LU Y C, CHOU J C K. Eight-space quaternion approach for robotic hand-eye calibration[C]//Proceedings of IEEE International Conference on Systems, Man and Cybernetics. BC: IEEE, 1995, 4:3316-3321.
( 0) 0)
|
| [5] |
CHEN H H. A screw motion approach to uniqueness analysis of head-eye geometry[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR'91). Maui, HI: IEEE, 1991:145-151.
( 0) 0)
|
| [6] |
DANIILIDIS K. Hand-eye calibration using dual quaternions[J].
The International Journal of Robotics Research , 1999, 18 (3) : 286-298 DOI:10.1177/02783649922066213 ( 0) 0)
|
| [7] |
ZHAO Z, LIU Y. A hand-eye calibration algorithm based on screw motions[J].
Robotica , 2009, 27 (2) : 217-223 DOI:10.1017/S0263574708004608 ( 0) 0)
|
| [8] |
ZHUANG H, Shiu Y C. A noise-tolerant algorithm for robotic hand-eye calibration with or without sensor orientation measurement[J].
IEEE Transactions on Systems, Man and Cybernetics , 1993, 23 (4) : 1168-1175 DOI:10.1109/21.247898 ( 0) 0)
|
| [9] |
FA I, LEGNANI G. Hand to sensor calibration: a geometrical interpretation of the matrix equation AX=XB[J].
Journal of Robotic Systems , 2005, 22 (9) : 497-506 DOI:10.1002/(ISSN)1097-4563 ( 0) 0)
|
| [10] |
PARK F C, MARTIN B J. Robot sensor calibration: solving AX=XB on the Euclidean group[J].
IEEE Transactions on Robotics and Automation , 1994, 10 (5) : 717-721 DOI:10.1109/70.326576 ( 0) 0)
|
| [11] |
HORAUD R, DORNAIKA F. Hand-eye calibration[J].
The International Journal of Robotics Research , 1995, 14 (3) : 195-210 DOI:10.1177/027836499501400301 ( 0) 0)
|
| [12] |
DORNAIKA F, HORAUD R. Simultaneous robot-world and hand-eye calibration[J].
IEEE Transactions on Robotics and Automation , 1998, 14 (4) : 617-622 DOI:10.1109/70.704233 ( 0) 0)
|
| [13] |
STROBL K H, HIRZINGER G. Optimal hand-eye calibration[C]//Proceedings of IEEE/RSJ Conference on Intelligent Robots and Systems. Beijing, China: IEEE, 2006: 4647-4653.
( 0) 0)
|
| [14] |
ZHAO Z. Hand-eye calibration using convex optimization[C]//Proceedings of IEEE International Conference on Robotics and Automation (ICRA 2011). Shanghai, China: IEEE, 2011: 2947-2952.
( 0) 0)
|
| [15] |
IKEUCHI K.
Computer vision: a reference guide[M]. Berlin, Germany: Springer Link Press, 2016 : 355 -358.
( 0) 0)
|
| [16] |
RUKAND T, DIETMAYER K. Globally optimal hand-eye calibration under free choice of cost-function[C]//Proceedings of IEEE International Conference on Consumer Electronics.Berlin, Germany: IEEE, 2012: 1-5.
( 0) 0)
|
| [17] |
HELLER J, HENRION D, PAIDLA T. Hand-eye and robot-world calibration by global polynomial optimization[C]//Proceedings of IEEE International Conference on Robotics and Automation (ICRA 2014). Hong Kong, China: IEEE, 2014: 3157-3164.
( 0) 0)
|
| [18] |
HELLER J, HENRION D, PAIDLA T. Globally optimal hand-eye calibration using branch-and-bound[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence , 2015 (1) : 1 ( 0) 0)
|
| [19] |
KANATANI K. Statistical optimization for geometric estimation: minimization vs. non-minimization[C]//Proceedings of IEEE International Conference on Pattern Recognition. Stockholm, Sweden: IEEE, 2014: 1-8.
( 0) 0)
|
| [20] |
NEUDECKER H. A note on Kronecker matrix products and matrix equation systems[J].
SIAM Journal on Applied Mathematics , 1969, 17 (3) : 603-606 DOI:10.1137/0117057 ( 0) 0)
|
| [21] |
ANDREFF N, HORAUD R, ESPIAU B. On-line hand-eye calibration[C]//Proceedings of 2nd International Conference on 3-D Digital Imaging and Modeling. Ottawa, Canada:IEEE, 1999: 430-436.
( 0) 0)
|
| [22] |
SCHMIDT J, NIEMANN H. Data selection for hand-eye calibration: a vector quantization approach[J].
The International Journal of Robotics Research , 2008, 27 (9) : 1027-1053 DOI:10.1177/0278364908095172 ( 0) 0)
|
| [23] |
ZHANG Z. A flexible new technique for camera calibration[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence , 2000, 22 (11) : 1330-1334 DOI:10.1109/34.888718 ( 0) 0)
|
| [24] |
IGEL C, TOUSSAINT M, WAN W. Rprop using the natural gradient[M]//Trends and applications in constructive approximation. Boston, U S A: Birkhäuser Basel, 2005: 259-272.
( 0) 0)
|
| [25] |
NESTEROV Y, NEMIROVSKII A, YE Y.
Interior-point polynomial algorithms in convex programming[M]. Philadelphia, U S A: Society for Industrial and Applied Mathematics, 1994 .
( 0) 0)
|



