网络中总是伴随着异常, 其产生的异常流量不仅影响着骨干网络的性能, 还影响着终端用户的安全。对ISP、网络管理人员和数据中心来说, 网络流分类和异常检测具有十分重要的现实意义[1]。近年来, 一些学者使用机器学习的方法进行流量分类研究。MOORE A等人提出一个网络流特征集合[2], 包含248个特征, 该特征集合在网络流分类领域得到广泛应用。LI Wei等人使用C4.5决策树算法来处理网络流分类问题[3]。MOORE A等人使用朴素贝叶斯方法来对网络流进行分类[4]。KIM H等人对基于端口、主机行为和流特征的3种分类方法进行比较[5], 并且比较7种基于流特征的分类方法, 最终SVM方法在所有的数据集中效果最好。NGUYEN T等人对机器学习算法在网络流分类中的应用进行概述, 并对2004—2007年的主要研究进行对比和总结[6]。
特征选择能够去除冗余特征, 避免维数灾难, 在不损失分类准确率的同时, 提高建模速度。ZHAO Zheng等人将特征选择方法总结为过滤式、封装式和嵌入式3种, 并对3种方法进行举例说明[7]。KATAKIS I等人首次对数据流动态特征空间的特征选择问题进行研究[8]。WENERSTROM B等人提出一种名为特征适应集成技术的增量特征选择和排序方法, 设计集成分类器对无标记数据进行分类[9]。MASUD M等人针对数据流分类中出现的新类别的问题提出一种称为DXMiner的技术[10]。YANG Longqi等人提出基于lasso的异常流检测方法, 在求解lasso问题时选择快速欧基里得投影方法, 提高了计算效率[11]。同时, 在线算法的研究也取得相应的成果。1960年, WIDROW B等人提出机器学习领域最早的在线学习算法, 即神经网络中的delta学习规则[12]。早期的感知器算法也是一种在线分类算法[13-14]。WANG Jialei等人提出一种在线特征选择算法[15]。关于在线学习的研究还有很多[16-21], 这里不再详述。目前, 研究者对于网络流本身的大规模性和时序性特点的关注还是不够。在线算法由于一次只处理一个样本或一小批样本, 该特点正好可以与网络流的时序性特点相结合, 同时, 其运行时间快, 能满足网络流异常检测的实时性要求, 另外, 其占用内存资源少, 能处理大规模网络流数据。本研究在在线过程中融入特征选择, 提出基于在线特征选择的网络流异常检测方法, 将在线算法的优点充分应用到网络流处理中。
1 在线特征选择算法描述网络流异常检测是一个二分类问题, 输入样本为{(xt, yt)|t=1, …, T}, 其中xt∈Rd是一个d维向量, 在本研究的试验数据中, d=248, yt∈{-1, +1}, -1表示异常样本(异常流量), +1表示正常样本(正常流量), T表示样本数量。本研究的目标是设计一个在线特征选择算法对样本进行分类, 要求时间快且错误率低。
1.1 在线特征选择在线算法由批处理算法改进而来。给定T个d维数据x1, …, xT, 一般的批处理学习算法可表述为求解如下的约束最优化问题:
| $\begin{gathered} \mathop {\min }\limits_w \left\{ {L\left( {\boldsymbol{w},{\boldsymbol{x}_1},\cdots ,{\boldsymbol{x}_T},\mu } \right) + \lambda R\left( {\boldsymbol{w},{\boldsymbol{x}_1},\cdots ,{\boldsymbol{x}_T},\theta } \right)} \right\},\\ {\text{s}}{\text{.t}}{\text{.}}\;\;\boldsymbol{w} \in \Omega . \\ \end{gathered} $ | (1) |
其中:w为要优化的向量参数; Ω表示可行解, 由约束集确定; μ、θ是两个参数。目标函数第一项L(·)刻画损失函数, 第二项R(·)是正则化项, 刻画问题的先验信息或对问题的约束, 使模型能够满足实际问题的需要, λ是一个正则化参数, 它控制着第一项和第二项的折中。在批处理学习情况下, 数据矩阵x被整体输入处理, 而在在线学习情况下, 数据x1, x2…, xT有序到达, 此时, 式(1)中的目标函数应该满足可分的性质, 即损失函数可以写成各样本的函数和
| $\begin{gathered} \mathop {\min }\limits_w \left\{ {L\left( {\boldsymbol{w},{\boldsymbol{x}_i},\mu } \right) + \lambda R\left( {\boldsymbol{w},{\boldsymbol{x}_i},\theta } \right)} \right\},\\ {\text{s}}{\text{.t}}{\text{.}}\;\;\boldsymbol{w} \in \Omega . \\ \end{gathered} $ | (2) |
式(2)即为在线学习的一般模型框架。
网络流异常检测属于一个二分类问题, 分类结果包括正常样本和异常样本, 在选择模型时, 首先考虑使用线性分类函数y=wtTxt作为模型函数进行试验, 分类器可以表示为sgn(wtTxt), 试验效果很好, 平均分类准确率可以达到95%, 试验表明网络流异常检测是一个线性可分问题, 加上线性模型比较简单易懂且建模速度快, 所以, 最终选择线性分类模型。确定模型后, 本研究损失函数选择hinge损失L(wt, xt)=max{0, 1-yt(wtTxt)}, 正则化项选择
| $\mathop {\min }\limits_{{\boldsymbol{w}_t}} \left( {\max \left\{ {0,1 - {y_t}\left( {\boldsymbol{w}_t^{\text{T}}{\boldsymbol{x}_t}} \right)} \right\} + \frac{\lambda }{2}{{\left\| {{\boldsymbol{w}_t}} \right\|}^2}} \right)。$ | (3) |
接下来使用梯度下降法优化式(3)的目标函数, 由于目标函数是一个二次凸函数, 所以使用梯度下降法优化时不存在局部最小情况。式(3)对w求梯度得:
| ${\nabla _t} = \lambda {\boldsymbol{w}_t} - {\boldsymbol{y}_t}{\boldsymbol{x}_t}$ | (4) |
梯度下降法的更新规则为
| ${\boldsymbol{w}_{t + 1}} = {\boldsymbol{w}_t} - \eta {\nabla _t},$ | (5) |
其中:η为步长;
| ${\boldsymbol{w}_{t + 1}} = \left( {1 - \eta \lambda } \right){\boldsymbol{w}_t} + \eta {y_t}{\boldsymbol{x}_t},$ | (6) |
至此, 已经完成在线过程, 却没有达到特征选择的目的, 接着考虑特征选择。
特征选择的思想是首先将分类器限制到L1球内, 然后用截断函数选择数值较大的特征维。在选择特征时, 目标是希望未被选择的特征对应的wt分量足够小, 从而提高分类准确率。文献[22]提出如下引理:
引理1 对于q>1且x∈Rd, 有
| ${\left\| {x - {x^m}} \right\|_q} \leqslant {\xi _q}{\left\| x \right\|_1}{\left( {m + 1} \right)^{1/q - 1}},m = 1,\cdots ,d,$ |
其中:ξq是1个只跟q有关的常数; xm表示保留向量x中较大的m个元素, 其他元素置0。
引理1表明当向量x在一个L1球内时, 它的值主要集中在比较大的元素中, 移除比较小的元素后, 对原始向量的影响很小, 因此, 使用稀疏投影方法将分类器投影到L1球内, 例如, ΔR={w∈Rd:‖w‖1≤R}, 其中:ΔR表示将w投影到半径为R的球内,接着用一个截断函数来控制特征选择的数量, 截断函数对wt分量的绝对值进行排序, 然后保留最大的M(特征选择的数量)个元素, 其他元素置0, 从而达到特征选择的目的。
1.2 在线特征选择算法基于1.1的策略, 得出在线特征选择算法见算法1。
算法1 在线特征选择算法(OFS)
1 输入:λ, η, M, (xt, yt);
2 初始化: w1=0;
3 for t=1, 2, …, T;
4 根据xt计算sgn(wtTxt)并与yt比较;
5 计算损失
6 if
7 wt+1=(1-λη)wt+ηytxt;
8 wt+1=
9 wt+1=Truncate(wt+1, M);
10 else wt+1=wt;
11 end if;
12 end for;
13 输出w。
算法1中调用一个截断算法, 见算法2。
算法2 w=Truncate(w, M)
1 if ‖w‖0>M;
2 w=wM, wM表示保留w中M个绝对值较大元素, 其余置0;
3 else w=w;
4 end if;
5 return w。
2 试验结果与分析 2.1 数据集本研究引用文献[11]中的数据, 其数据来源于WIDE数据库[23], 该数据库维护太平洋骨干网流量, 数据采样时间为20110109T1400—20110109T1415, 统计信息见表 1。
| 表 1 原始数据流统计信息 Table 1 Traffic trace statistics |
根据原始报文首部的五元组信息(协议、源地址、目的地址、源端口号、目的端口号)对数据流进行聚合, 将原始报文组织成流数据, 然后根据Moore特征提取方法提取248维特征, 形成试验数据, 最后将数据按序划分为10个数据集。本研究选取6个数据集作为试验数据, 并按4:1划分为训练集和测试集, 另外, 为了进行参数选择试验, 选取数据集01中的测试集作为验证集, 数据集的比例大小见表 2。
| 表 2 数据集大小 Table 2 The sample size of datasets |
在网络流分类与异常检测中, 异常样本往往比较少, 存在类不平衡的情况, 只使用准确率来评价分类器的效果是不合理的, 因此, 需要引入其他评价指标。
假设P表示正类样本数量, N表示负类样本数量, 在引入其他指标之前, 先对构成这些指标的4个基本术语进行解释:真阳性(true positive, TP)、真阴性(true negative, TN)、假阳性(false positive, FP)和假阴性(false negative, FN)。真阳性是指被分类器正确分类的正类样本数量, 真阴性是指被分类器正确分类的负类样本数量, 假阳性是指被分类器错分为正类的负类样本数量, 假阴性是指被分类器错分为负类的正类样本数量。
本研究采用5个评价指标, 分别为准确率(Accuracy)、召回率(Recall)、假阳性率(FPR)、精度(Precision)和F度量(F-measure)。准确率是指分类器正确分类的样本所占的比例, 计算公式如下:
| ${\text{Accuracy = }}\frac{{{\text{TP + TN}}}}{{P + N}},$ | (7) |
召回率是指被分类器正确识别的正类样本的比例, 计算公式如下:
| ${\text{Recall = TPR}} = \frac{{{\text{TP}}}}{{{\text{TP + TN}}}},$ | (8) |
假阳性率是指被分类器错误识别为正类样本的负类样本占所有被识别为负类样本的比例, 计算公式如下:
| ${\text{FPR = }}\frac{{{\text{FP}}}}{{{\text{FP}} + {\text{TN}}}},$ | (9) |
精度是指被分类器识别为正类样本占实际为正类样本的比例, 计算公式如下:
| ${\text{Precision = }}\frac{{{\text{TP}}}}{{{\text{TP}} + {\text{FP}}}},$ | (10) |
精度与召回率通常呈现一个逆关系, 可以使用F度量将二者组合起来, 计算公式如下:
| $F - {\text{measure}} = \frac{{2 \times {\text{Precision}} \times {\text{Recall}}}}{{{\text{Precision}} + {\text{Recall}}}}。$ | (11) |
在对比试验中, 将采用本节提到的所有指标来评估分类器的性能, 全面评价异常检测的效果。
2.3 试验设计本研究设计3个试验来验证在线特征选择算法的有效性, 首先, 在6个数据上运行OFS算法, 验证OFS算法的可行性, 并调整算法参数以达到最好效果。然后, 将样本顺序打乱, 破坏样本的时序性, 再运行OFS算法, 验证分类准确率与样本时序性的关系。最后, 在相同特征子集下, 将OFS算法与经典的批处理特征选择算法进行比较。
2.4 试验结果与分析 2.4.1 OFS算法在网络流异常检测中的性能设定正则化参数λ=10-4, 步长η=1.5, 特征选择数量M=25个, 在6个数据集上运行OFS算法, 得到训练和测试准确率随样本规模的变化见图 1。

|
图 1 OFS算法的训练和测试性能 Figure 1 Performance of OFS in the training and testing process |
由图 1可知, OFS算法在训练过程中, 当迭代次数小于100次时, 训练错误率较高, 但随着迭代次数的增加, 模型不断学习, 训练准确率不断提高, 最后达到稳定状态, 而测试准确率基本上很稳定。
训练和测试准确率的统计柱状图见图 2。
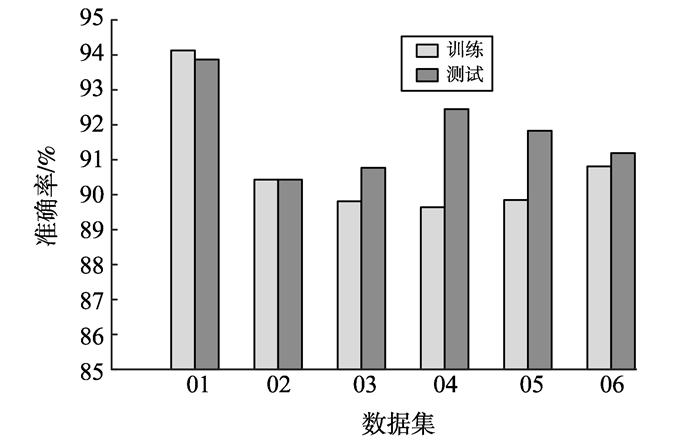
|
图 2 在线特征选择算法的训练和测试准确率 Figure 2 The accuracy of OFS in the training and testing process |
由图 2可知, 测试准确率在大多数情况下比训练准确率高, 且均在90%以上, 训练准确率维持在90%左右, 初步验证了OFS算法在网络流异常检测中的可行性。
为了选择合适的参数, 设定M=25个, λ分别取10-1, 10-2, …, 10-6, η分别取0.2, 0.4, 0.6, …, 3, 使用数据集01的训练集对模型进行训练, 训练完成后使用验证集进行参数选择, 得到验证准确率随参数的变化结果见图 3。
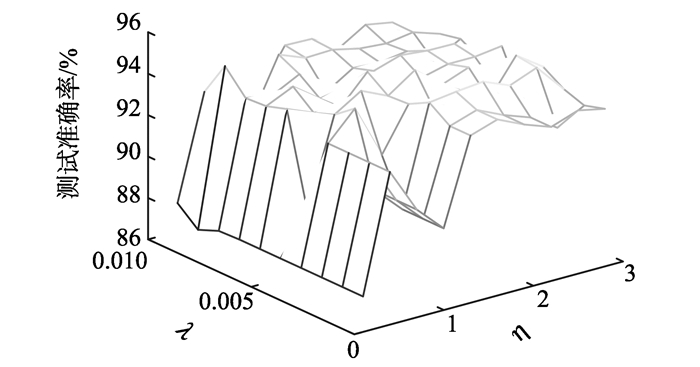
|
图 3 OFS算法在验证集上的参数选择 Figure 3 Parameter selection of OFS on verification dataset |
从图 3可知, 验证准确率随着参数的变化而变化, 当λ=0.003, η=2.5时, 验证准确率相对较高。
设定λ=10-4, η=1.8, 分别选择5、10、20、50、100、200和248个特征在6个数据集上运行OFS算法, 得到测试准确率与特征选择数量的关系见表 3。
| 表 3 OFS算法在不同特征子集下的测试准确率 Table 3 The testing accuracy of OFS with different feature subset |
从表 3可知, 数据集01、05和06在选择50个特征时测试准确率较高, 数据集02和04在选择20个特征时测试准确率较高, 数据集03在选择10个特征时测试准确率较高, 当使用全部特征(248维)时, 其测试准确率在所有数据集上都相对较低。由于特征之间存在冗余性和相关性, 导致使用全部特征时分类性能反而不好, 而特征选择可以去除冗余和无用的特征, 在不损失分类准确率的同时, 提高建模速度。
2.4.2 OFS算法性能与样本时序性的关系由于网络流具有时序性, 样本有序到达, 而在线算法恰好可以很好地利用其时序性。首先使用有序数据运行算法, 然后将数据顺序随机打乱, 再运行算法, 得到两次的测试准确率见图 4。

|
图 4 OFS算法在有序和无序数据集上的测试准确率 Figure 4 The testing accuracy of OFS with ordered and random dataset |
从图 4可知, 在数据集01、04、05和06上, 有序样本的准确率比无序高, 在数据集02和03上相反。可能在采集数据集02和03时, 网络中的某些行为比较活跃, 使数据的分布规律被破坏, 导致时序性失去意义。
2.4.3 OFS算法与经典批处理算法的比较选择3个批处理特征选择算法进行对比试验:Fisher得分(fisher score)、基尼指数(gini index)和方差得分(variance score)。Fisher得分根据类标信息来选择特征。基尼指数是衡量一个特征区分不同类别能力的指标。方差得分根据特征的方差来判断, 保留方差较大的特征, 舍弃方差较小的特征。它们均属于过滤式特征选择算法, 在特征选择之后, 选择SVM来分类, SVM的参数使用10折交叉验证选择, 试验数据选择数据集01。
Fisher得分、基尼指数和方差得分分别选择5、15、25、35和45个特征, 然后使用SVM做分类器, 再与OFS算法进行对比, 根据准确率、召回率、假阳性率、精度和F-度量来评价其性能。
首先, 比较测试准确率, OFS与其他3个算法在不同特征子集上的测试准确率见表 4。
| 表 4 OFS与批处理算法在不同特征子集上的测试准确率 Table 4 The testing accuracy between OFS and others batch algorithms |
由表 4可知, 当选择5、15、25和35个特征时, OFS的测试准确率比其他3个批处理算法略低, 选择45个特征时, 其测试准确率比其他算法高。由于在线特征选择算法一次只处理一个样本, 处理完后将其扔掉, 而批处理则考虑所有样本, 所以在线算法的准确率比批处理略低。
然后, 比较运行时间, OFS与其他算法在不同特征子集上的运行时间见表 5。
| 表 5 OFS与批处理算法在不同特征子集上的运行时间 Table 5 The running time costs between OFS and others batch algorithmss |
从表 5可知, OFS算法在时间性能上明显优于批处理算法, 其运行时间在不同特征子集上均不足1 s。
运行时间变化趋势见图 5, 由于Gini指数运行时间超过170 s, 不便于与其他算法比较变化趋势, 所以图 5中没有考虑Gini指数。
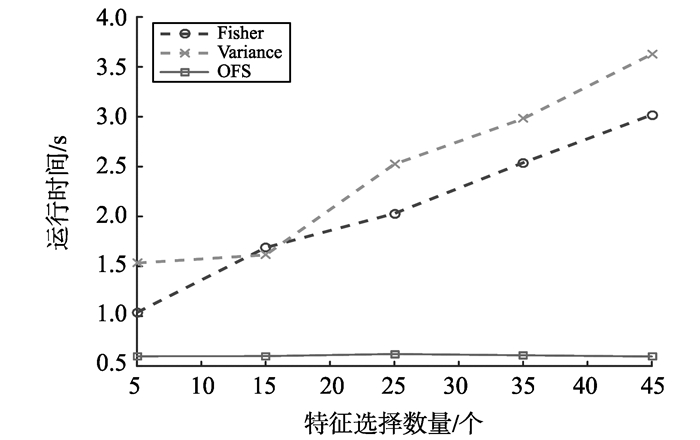
|
图 5 OFS与批处理算法在不同特征子集上运行时间的变化趋势 Figure 5 The change tendency of time between OFS and batch algorithms |
从图 5可知, 随着特征子集数量的增加, 批处理算法的运行时间也不断增加, 而OFS几乎保持不变, 所以, OFS算法能满足网络流异常检测的实时性要求。
最后, 从假阳性率、召回率、精度和F度量这4个指标来比较OFS与其他3个批处理算法的性能, 试验结果见图 6。

|
图 6 OFS和批处理在不同特征子集上的评价指标 Figure 6 The performance of four metrics both OFS and batch algorithms |
假阳性率是异常检测中重点关注的指标之一, 异常流量容易湮没在正常流量中, 尤其是在骨干网流量大速率快的情况下, 要求异常流量的FP尽量小。从图 6(a)可知, 当选择5、15和45个特征时, OFS的假阳性率较低, 选择25和35个特征时比批处理算法略高。
召回率是指被正确分类的正常流量的比例, 从图 6(b)可知, 当选择5和15个特征时, OFS的召回率较低, 不如批处理, 但选择25、35和45个特征时, 其表现胜过批处理算法。
精度是指被识别为正类的样本中实际为正类样本的比例, 从图 6(c)可知, OFS在5、15和45个特征的情况下表现较好, 在25和35个特征时不如批处理。
F-度量将召回率与精度进行组合, 从图 6(d)可知, OFS在选择45个特征时, 其F-度量相对较高, 其他特征子集下表现不如批处理。
总的来说, OFS算法在大多数情况下的性能优于批处理, 在少数情况下, 其性能不及批处理, 但很接近。
3 结语传统的批处理方法捕捉不到骨干网络流的时序性特点, 且当数据规模很大时, 批处理方法几乎不能有效工作。针对骨干网络流的时序性和大规模性的特点, 本研究提出一种在线特征选择方法, 通过与批处理对比, 在线特征选择能很好地利用网络流数据的时序性特点, 另外, 其运行时间明显优于批处理方法, 能满足实时性要求, 同时, 在准确率上与批处理算法相近。本研究为网络流分类和异常检测提供一种全新的思路, 在线方法在网络流上的应用值得进一步深入研究。接下来的研究中, 可以考虑在多任务模式下设计在线特征选择算法, 同时, 也可以将本研究的方法加以改进, 应用于网络流多分类领域, 另外, 网络流的时序性特点还有待进一步深入研究。
| [1] |
杨龙琪.网络安全态势感知关键技术研究[D].南京:中国人民解放军理工大学, 2015.
YANG Longqi. Key techniques of network security situation awareness[D]. Nanjing: PLA University of Science and Technology, 2015. (  0) 0)
|
| [2] |
MOORE A, ZUEV D, CROGAN M. Discriminators for use in flow-based classification[R]. UK: Computer Science Department, Queen Mary University of London, 2005.
( 0) 0)
|
| [3] |
LI Wei, MOORE A. A machine learning approach for efficient traffic classification[C]//Proceedings of 15th International Symposium on MASCOTS′07. Istanbul, Turkey: IEEE Press, 2007:310-317.
( 0) 0)
|
| [4] |
MOORE A, ZUEV D. Internet traffic classification using bayesian analysis techniques[J].
Acm Sigmetrics Performance Evaluation Review , 2005, 33 (1) : 50-60 DOI:10.1145/1071690 ( 0) 0)
|
| [5] |
KIM H, CLAFFY K, FOMENKOV M, et al. Internet traffic classification demystified: myths, caveats, and the best practices[C]//Proceedings of the 2008 ACM CoNEXT Conference. Madrid, Spain: ACM Press, 2008:1-12.
( 0) 0)
|
| [6] |
NGUYEN T, ARMITAGE G. A survey of techniques for internet traffic classification using machine learning[J].
Communications Surveys & Tutorials , 2008, 10 (4) : 56-76 ( 0) 0)
|
| [7] |
ZHAO Zheng, MORSTATTER F, SHARMA S, et al. Advancing feature selection research[R]. USA:School of Computing, Informatics, and Decision Systems Engineering, Arizona State University, 2010.
( 0) 0)
|
| [8] |
KATAKIS I, TSOUMAKAS G, VLAHAVAS I. On the utility of incremental feature selection for the classification of textual data streams[C]//Proceedings of the 10th Panhellenic Conference on Informatics. Volos, Greece: Springer Berlin Heidelberg Press, 2005:338-348.
( 0) 0)
|
| [9] |
WENERSTROM B, GIRAUD-CARRIER C. Temporal data mining in dynamic feature spaces[C]//Proceedings of the Sixth ICDM′06. Hong Kong, China: IEEE Computer Society Press, 2006:1141-1145.
( 0) 0)
|
| [10] |
MASUD M, CHEN Q, GAO J, et al. Classification and novel class detection of data streams in a dynamic feature space[C]//Proceedings of the 2010 European Conference on Machine Learning and Knowledge Discovery in Databases. Barcelona, Spain: Springer Berlin Heidelberg Press, 2010:337-352.
( 0) 0)
|
| [11] |
YANG Longqi, HU Guyu, LI Dong, et al. Anomaly detection based on efficient Euclidean projection[J].
Security and Communication Networks , 2015, 8 (17) : 3229-3237 DOI:10.1002/sec.v8.17 ( 0) 0)
|
| [12] |
WIDROW B, HOFF M E. Adaptive switching circuits[C]//Proceedings of the 1960 IRE WESCON Convention Record. Los Angeles, USA: Institute of Radio Engineers Press, 1960:96-104.
( 0) 0)
|
| [13] |
ROSENBLATT F. The perceptron: a probabilistic model for information storage and organization in the brain[J].
Psychological Review , 1958, 65 (6) : 386-408 DOI:10.1037/h0042519 ( 0) 0)
|
| [14] |
FREUND Y, SCHAPIRE R E. Large margin classification using the perceptron algorithm[J].
Machine Learning , 1999, 37 (3) : 277-296 DOI:10.1023/A:1007662407062 ( 0) 0)
|
| [15] |
WANG Jialei, ZHAO Peilin, HOI S C H, et al. Online feature selection and its applications[J].
Knowledge and Data Engineering , 2014, 26 (3) : 698-710 DOI:10.1109/TKDE.2013.32 ( 0) 0)
|
| [16] |
ABERNETHY J, BARTLETT P, RAKHLIN A. Multitask learning with expert advice[C]//Proceedings of the 2007 COLT. San Diego, USA: Springer Berlin Heidelberg Press, 2007:484-498.
( 0) 0)
|
| [17] |
LUGOSI G, PAPASPILIOPOULOS O, STOLTZ G. Online multi-task learning with hard constraints[C]//Proceedings of the COLT′09. Montreal, Canada: ACL Press, 2009:315-320.
( 0) 0)
|
| [18] |
WARMUTH M K, KUZMIN D. Online variance minimization[J].
Machine Learning , 2012, 87 (1) : 514-528 ( 0) 0)
|
| [19] |
DEKEL O, GILAD-BACHRACH R, SHAMIR O, et al. Optimal distributed online prediction using mini-batches[J].
The Journal of Machine Learning Research , 2012, 13 (1) : 165-202 ( 0) 0)
|
| [20] |
JAIN P, KULIS B, DHILLON I S, et al. Online metric learning and fast similarity search[C]//Proceedings of the NIPS′09. Vancouver, Canada: NIPS Foundation Press, 2009:761-768.
( 0) 0)
|
| [21] |
BORDES A, ERTEKIN S, WESTON J, et al. Fast kernel classifiers with online and active learning[J].
The Journal of Machine Learning Research , 2012, 6 (3) : 1579-1619 ( 0) 0)
|
| [22] |
DONOHO D L. Compressed sensing[J].
Information Theory , 2006, 52 (4) : 1289-1306 DOI:10.1109/TIT.2006.871582 ( 0) 0)
|
| [23] |
FONTUGNE R, BORGNAT P, ABRY P, et al. Mawilab: combining diverse anomaly detectors for automated anomaly labeling and performance benchmarking[C]//Proceedings of the 2010 ACM CoNEXT conference. Philadelphia, USA: ACM Press, 2010:1-12.
( 0) 0)
|




