2. 中国科学院自动化研究所, 北京 100190
2. Institute of Automation, Chinese Academy of Sciences, Beijing 100190, China
过去的研究工作中, 运动界面的建模方式主要分为隐式与显式两种。隐式界面也称等值面方法, 理念是建立一个3维网格, 在所有网格顶点上存储到界面的有向距离值φ, 通过追踪φ的变化来追踪界面。OSHER S等人最早开展等值面追踪领域的研究[1], OSHER S与刘儒勋等人对等值面方法进行较为详细的描述[2-3]。JIANG G S等人提出无振荡(ensured no oscillation, ENO)方法[4], SELLE A等人提出一种无条件稳定的Macomark方法[5], SETHIAN J提出FastMarching方法[6]。ZHAO Hongkai的FastSweep方法可以快速重新初始化等值面[7], 周勇等人提出一种构造自适应等值面的方法[8]。在等值面应用实例的研究工作中, 杨猛等人提出一种基于等值面的曲线演化方法[9], FOSTER N与ENRIGHT D等人将等值面方法应用于流体动画中[10-11]。BARGTEIL A W等人在八叉树网格上追踪流体界面[12], LOSASSO F等人提出了针对多相混合流体的等值面投影方法[13], ZHENG W和KIM B等人提出Regional Level Set方法, 实现了任意多相流的等值面重构[14-15]。
隐式界面的弊端在于当界面的细节规模低于距离场网格单元的大小时, 细节就会在重构过程中丢失。相反的, 直接追踪显式界面的优势在于可以不受网格分辨率的约束, 能较好地保持界面上尖锐的几何, 这一点对于模拟液体界面非常重要。目前显式界面算法大致分为两类, 一种是基于碰撞检测的方法, 如BROCHU T等人的El topo软件库[16], 一种是重构显式界面的方法, 如MÜLLER M的全局重构法与WOJTAN C等人的局部重构法[17-20]。由于基于碰撞检测的方法非常耗时, 因此本研究的算法是基于局部重构的, 因为局部重构法效率高, 且对关键细节的维护不比碰撞算法差。
1 算法总览定义显式界面为M, M是满足流形特性的闭合三角形网格。M的基本数据结构为描述基本几何元素的顶点集V, 边集E以及面集F, 外加若干描述这些几何元素邻接关系的数据集。
本研究的算法使用水平集(Level Set)方案中的有向距离场(signed distance field, SDF)函数来检测界面发生拓扑变化的空间区域。SDF函数定义在覆盖仿真区域的空间网格上。在图形学领域中, 网格的一个单元常被称为“体素”。SDF将顶点到界面M的有向距离离散存储在每个体素的顶点上。其中, 在M包围的空间区域内部, SDF为负值, 在区域外部SDF为正值。在每个解算步, 算法的流程如下:
(1) 移动Lagrangian界面;
(2) 将界面投影到体素网格上, 并初始化SDF;
(3) 找到界面产生拓扑错误的区域所包含的体素;
(4) 通过界面的局部细分, 裁剪替换与缝合操作来完成局部重构, 得到最终的界面。
2 界面追踪与拓扑事件处理 2.1 移动Lagrangian界面本研究的算法在驱动显式表面时需要一个定义在计算空间的速度场, 这个场可以由外部的物理解算程序(如随机噪声生成器、流体解算器等)提供。
更新M位置的方法为不考虑几何元素之间邻接关系的变化, 直接计算V中每个顶点的新位置。算法采用3阶Runge-Kutta时间积分法在速度场中移动顶点。即对顶点v, 假设它的初始位置为p, Δt时刻后的新位置为p′, 则有:
| ${p_1} = p + 0.5\Delta tU\left( p \right),$ | (1) |
| ${p_2} = p + 0.75\Delta tU\left( {{p_1}} \right),$ | (2) |
| $p' = p + \Delta t\left( {\frac{2}{9}U\left( p \right) + \frac{3}{9}U\left( {{p_1}} \right) + \frac{4}{9}U\left( {{p_2}} \right)} \right),$ | (3) |
其中: U(X)表示在X位置的速度向量; p1与p2是两个临时中间位置。如果用户提供的速度场是离散存储在笛卡尔规则网格上的, 则插值函数可以取线性插值。本研究的试验用例使用粒子流体, 插值函数使用高次样条函数, 形式为
| $U\left( X \right) = \frac{{\sum\limits_j {{u_j}w\left( {\frac{{\left| {X - {X_j}} \right|}}{R}} \right)} }}{{\sum\limits_j {w\left( {\frac{{\left| {X - {X_j}} \right|}}{R}} \right)} }},$ | (4) |
其中: w为权值; u为每个粒子携带的速度; R代表样条函数的影响半径(一般取粒子平均间距的2倍)。计算w可以使用高次样条函数(s为自变量), 本算法使用的函数为
| $w\left( s \right) = \left\{ \begin{gathered} 1 - 6{s^2} + 8{s^3} - 3{s^4},\forall s \leqslant 1, \hfill \\ \begin{array}{*{20}{c}} {0,}&{}&{}&{}&{}&{\forall s > 1.} \end{array} \hfill \\ \end{gathered} \right.$ | (5) |
本算法中, SDF的计算不是通过传统的Level Set方法来完成, 而是直接根据移动后的M来计算。本算法仅在距离M很近的区域内计算到M的精确距离, 然后外推至远离M的区域。设每个体素单元的边长为Dx, 具体的步骤如下:
Step 1 对每个网格顶点, 检查该点的临域(即[0, Dx]3的AABB包围盒)是否和M相交。如果相交便计算其到临近三角形的最近距离, 并标识该顶点;
Step 2 根据已经标识的顶点集, 使用Fast Sweep方法(见文献[7])来求解方程:
| $\left| {\nabla \varphi } \right| = 1,$ | (6) |
得到远离M的顶点的SDF值。
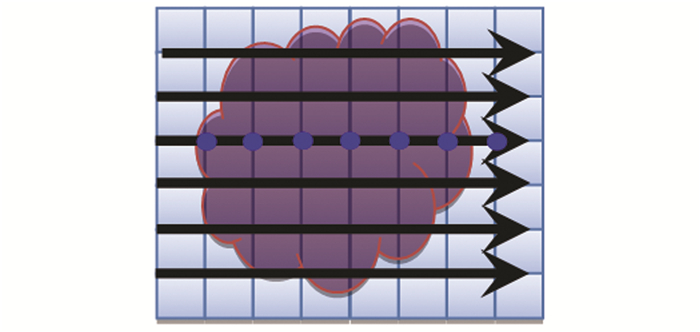
使用文献[17]提出的Ray-Marching方法来高效地检查界面产生拓扑错误的区域, 见图 1。
|
图 1 “内-外”测试2D示意图 Figure 1 2D illustration of "inside-outside" detection |
以x方向的Ray-Marching过程为例, 从体素网格的左侧面开始, 从该面上的每个体素顶点发射一条射线并沿x轴正向推进(见图 1长箭头), 每次推进的步长为Dx。求射线与M的交点。当射线与M的一个三角面相交时, 计算三角面的法线向量N与射线的方向向量的点积d, 如果d < 0, 说明射线从M的外部进入M的内部; 如果d>0, 说明射线从内部进入外部, d=0属于退化的情况(射线恰与M相切)。算法为每条射线设置一个计数器(见图 1圆点), 初始值为0。当d < 0时, 计数器加1, 当d>0时, 计数器减1。因此, 如果射线经过一个体素顶点时值为0, 说明该顶点处于M外部, 值为1说明该顶点处于内部; 如果值大于1说明附近的区域内M产生了规模为O(Dx)的自相交错误, 值小于0说明产生了三角形的翻转错误。
此外, 相对于体素的总数, 与M相交的体素的数量要少1个数量级, 而且每条射线的扫描过程都是独立的, 因此这个过程非常适合用并行计算来加速。
2.3 查找需要重构界面的体素M的拓扑错误主要是界面在发生合并或分离时产生的自相交, 本算法需要将这些错误定位在空间体素上。这里先给出几个定义:
定义1 如果某条体素边与M至少有2个交点, 则该边被认为是1个非法边。
定义2 如果某个体素面的4条边中有1条非法边, 或者该面与M的交线在该面上形成1条闭合的曲线, 则该体素面是1个非法面。
定义3 如果某个体素包含1个非法面, 则是1个非法体素。
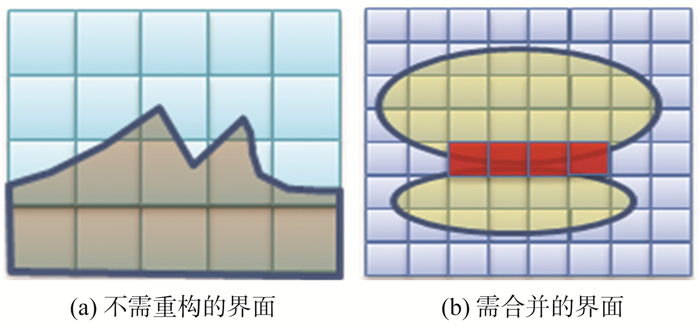
由于之前计算有向距离场的过程中已经得到所有体素边与M的交点信息, 因此通过检查相应的数据结构便可以找到所有的包含错误拓扑元素的体素。然而, 这些体素需要筛选, 见图 2。
|
图 2 发生拓扑事件的体素2D图示 Figure 2 2D illustration of voxels where topological events occur |
图 2(a)中, 尖锐的界面部分会与体素的一条边有多次相交, 但是这种情况并不需要重构界面, 图 2(b)中, 两个椭圆界面合并时, 接触面处的界面才需要重构。
本算法筛选体素的方法是:检查体素8个顶点的有向距离场的数值, 只有当值小于0的顶点超过6个时, 才认为有拓扑事件即将发生, 从而该体素处的界面需要重构, 因为此处可以认为是产生O(Dx)的自相交错误。将筛选出的这些非法体素称为“Re-sample体素”, 并将其存放在链表里。
局部重构过程是将Re-sample体素中的原始界面的三角网格替换成预定义的模板。因此一定要保证边界处的Re-sample体素与原始M的所有交点恰好能满足某个模板。因此将使用Flood-Fill算法, 从初始的Re-sample体素沿非法面的方向向外扩展, 将未标识为Re-sample的邻居体素作为Re-sample体素加入到链表中, 直到所有Re-sample体素的外边界面都不是非法面为止。这个过程见图 2(b)。
本研究采用的这种体素筛选方式倾向于处理潜在的界面合并拓扑事件, 而对于界面分离的拓扑事件, 只有在Ray-Marching中检测出自相交错误时才会去处理。这种方式比较适合液体仿真, 有利于维持稀薄水层不因界面重构而消失。
2.4 通过局部重构改变界面拓扑局部重构过程的关键是通过将体素和M的相交类型与本研究定义的重构模板匹配, 一旦匹配成功则就用模板来生成新的局部三角网格, 并将新的网格与原始网格在Re-sample体素的边界面上连接起来。该过程的算法可以分3个子过程, 分别为局部分割M、裁剪替换M与缝合M。
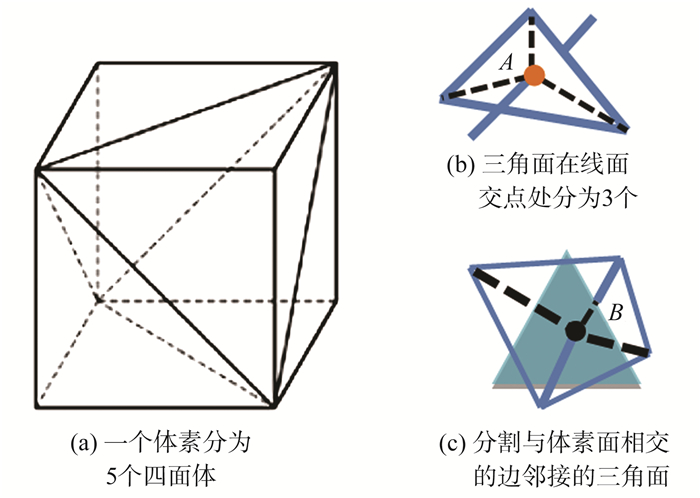
2.4.1 局部分割对M的局部细分为两个步骤, 见图 3。
|
图 3 体素细分与界面细分 Figure 3 Voxel subdivision and mesh subdivision |
对每个Re-sample体素→
Step 1 将该体素分为5个四面体, 见图 3(a)。
Step 2 对每个四面体→
(1) 找到M中所有与该四面体的6条边相交的三角形。对每个三角形, 在相交位置处添加1个新顶点, 并将该三角形分成3个新的三角形。这类新顶点称为A类顶点, 见图 3(b)。
(2) 找到M中所有与该四面体的4个面相交的边, 然后在交点位置处添加一个新顶点, 并将这条边邻接的两个三角形分成4个新的三角形。这类新顶点称为B类顶点, 见图 3(c)。
注意, Step1中四面体的每个顶点都是Re-sample体素的顶点, 因此这些顶点“内-外”状态是已知的(之前Ray-Marching的计算结果)。
2.4.2 裁剪与替换当局部分割操作完成之后, 对于Re-sample体素生成的所有四面体, M中不再存在与这些四面体的面交错或横截的三角形。换言之, 这些四面体周围的三角形或者完全在其内部, 或完全在其外部。此时, 算法将删除所有处于四面体内部的三角形, 这个删除的操作便可称之为“裁剪”。裁剪操作完成后, 算法遍历每个四面体, 根据顶点“内-外”状态, 来匹配预定义的模板。模板见图 4。
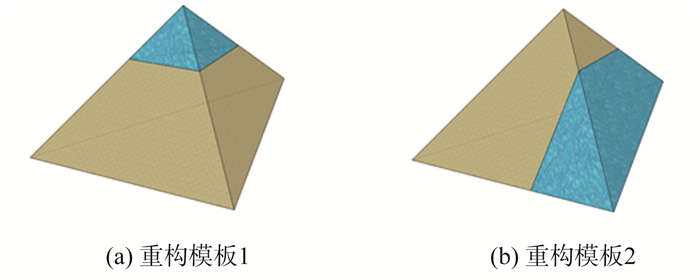
|
图 4 重构模板 Figure 4 Reconstruction template |
如果匹配成功, 则根据模板来连接四面体边上所有的A类顶点, 生成新的三角形。这个过程相当于在四面体内部用具有简单拓扑的界面替换原本有错误拓扑的界面。
2.4.3 缝合操作在Re-sample体素与非Re-sample体素相接的边界面上, 原始的M和边界面的交线与模板的边线一般是不相符的。因为局部重构时只用到了A类顶点来生成新三角形, 在每个边界面上交线是一条连接A类顶点的直线段; 然而原始的交线可能是一条由A类顶点与B类顶点连接起来的折线。因此, 缝合操作便是修改边界处的几何关系, 使新的交线与原始的交线重合, 这样新的界面便不会产生孔洞。
缝合操作的算法过程如下:
对需要缝合四面体的面→
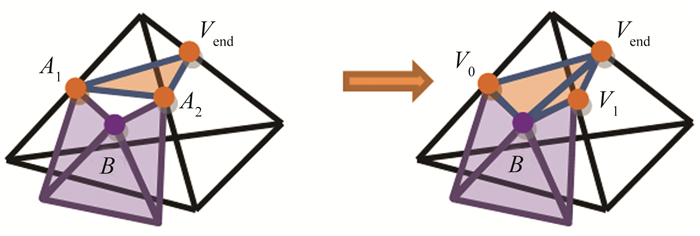
找出该面上的每条交线, 即顺次连接的A类与B类顶点形成的“链”, 首尾两端一定是A类顶点。
对每条交线链→
(1) 找到首尾两端的A类顶点(记为A1, A2)所在的模板三角型的第3个顶点Vend。
(2) 从链上的第1个顶点开始, 将该顶点从链上取下, 记为V0, 如果下1个B类顶点为V1, 则生成以V0、V1、Vend为顶点的新三角形该链的所有B类顶点访问完毕为止。
(3) 删除原本以A1, A2, Vend为顶点的三角形。
缝合M的过程示意见图 5。
|
图 5 界面边界缝合操作示意图 Figure 5 Sewing operation diagram of mesh boundary |
缝合算法不需对体素外没有拓扑错误的界面几何结构进行任何改动, 从而使整个算法的健壮性得到保证。
3 试验结果及讨论试验平台为DELL T550工作站, 12 G内存, 12核2.67 GHz的CPU。第一个试验用例是著名的Enright豁口球旋转试验, 见图 6。

|
图 6 Enright豁口球旋转试验 Figure 6 Rotation test of Enright semi-sphere |
其中图 6(a)的最高分辨率相当于是1503的规则体素网格; 图 6(b)使用了1003的规则体素网格; 图 6(c)使用803的规则体素网格; 而本研究方法仅使用643的规则体素网格。可以看到, 图 6(a)有着严重的几何平滑现象; 图 6(b)出现较为严重的变形, 整体上与初始的几何相差很大; 而图 6(c)通过修正粒子可以较好地保持整体的几何特征, 然而在曲率较大的豁口处依然产生了锯齿现象; 本研究方法基本没有平滑现象出现, 精确地保持了原有的几何特征。
第二个试验用例是扰动性很强的粒子液体模拟, 见图 7。

|
图 7 水球落入方形水池的模拟 Figure 7 Simulation of water ball falling into a square pool |
场景用于界面重构的体素网格分辨率为2503, 而用于流体解算的网格分辨率为1283。本算法解算一帧平均需要15~25 s, 其中用于界面追踪的时间约为8~11 s。从图 7可以看出, 对于拓扑变化非常剧烈的界面, 本研究的算法依然可以快速地处理合并、分离的拓扑事件, 形成无洞、无自相交的闭合界面, 而且界面处大量的高频细节都得到维护。
4 结论无论在计算机图形学领域里, 还是在计算物理、数值计算领域里, 自由界面的数值追踪方法一直都是一个重要的研究方向。然而, 模拟一个自由界面的运动很难通过速度场来直接驱动一个三角网格来完成, 因为速度场的数值误差很容易导致三角网格产生自相交错误, 在实际应用例如液体仿真中, 液体会产生合并、分离, 从而使界面的几何拓扑发生改变, 如果直接追踪一个显式的三角化界面, 则需要复杂的几何操作来处理这些拓扑事件。因此, 基于这类应用需求, 本研究通过给出一种可以快速处理复杂拓扑事件的显式界面追踪算法, 可以有效地消除显式三角网格的自相交错误, 始终使界面的三角网格保持闭合并且维持较好的三角形平均形态质量, 使得任意稀薄的表面细节不会因界面演化而被平滑掉, 显式界面复杂的拓扑变化可以得到高效的处理, 适合应用于液体的仿真动画或者布料、织物或者其他动态界面的运动模拟。然而, 本算法最适合的应用是体现液体和外部空气之间的界面细节, 目前还不能直接应用于不相溶混合液体的界面追踪, 因为属于不同液体的界面在碰撞时会因局部重构算法而自动发生合并。下一步的工作便是研究混合不相容液体的显式界面追踪算法, 这可以通过把显式界面同多相水平集算法结合起来, 对不同属性的界面加以标识来实现。
| [1] |
OSHER S, SETHIAN J. Fronts propagating with curvature-dependent speed: Algorithms based on hamilton-jacobi formulations[J].
Journal of Computational Physics , 1988, 79 (1) : 12-49 DOI:10.1016/0021-9991(88)90002-2 ( 0) 0)
|
| [2] |
OSHER S, FEDKIW R.
Level set methods and dynamic implicit surfaces[M]. New York, USA: Springer, 2003 .
( 0) 0)
|
| [3] |
刘儒勋, 王志峰.
数值模拟方法和运动界面追踪[M]. 安徽: 中国科学技术大学出版社, 2001 : 187 -190.
( 0) 0)
|
| [4] |
JIANG G S, PENG D. Weighted ENO schemes for hamilton jacobi equations[J].
SIAM Journal on Scientific Computing , 2000, 21 (6) : 2126-2143 DOI:10.1137/S106482759732455X ( 0) 0)
|
| [5] |
SELLE A, FEDKIW R, KIM B, et al. An unconditionally stable maccormack method[J].
Journal of Scientific Computing , 2008, 35 (2-3) : 350-371 DOI:10.1007/s10915-007-9166-4 ( 0) 0)
|
| [6] |
SETHIAN J. A fast marching level set method for monotonically advancing fronts[J].
Proceedings of National Academic Science , 1996, 93 (4) : 1591-1595 DOI:10.1073/pnas.93.4.1591 ( 0) 0)
|
| [7] |
ZHAO Hongkai. A fast sweeping method for eikonal equations[J].
Mathematics of computation , 2005, 74 (250) : 603-627 ( 0) 0)
|
| [8] |
周勇, 唐泽圣. 用自适应的三线性逼近方法构造等值面[J].
计算机学报 , 1994, 17 (S1) : 1-10 ZHOU Yong, TANG Zesheng. Adaptive trilinear approximation to isosurfaces of data sets in 3D space[J]. Chinese Journal of Computers , 1994, 17 (S1) : 1-10 (  0) 0)
|
| [9] |
杨猛, 汪国平, 董士海. 基于Level Set方法的曲线演化[J].
软件学报 , 2002, 13 (9) : 1858-1865 YANG Meng, WANG Guoping, DONG Shihai. Curves evolving based on level set method[J]. Journal of software , 2002, 13 (9) : 1858-1865 (  0) 0)
|
| [10] |
FOSTER N, FEDKIW R. Practical animation of liquids[C]// Proceedings of the 28th Annual Conference on Computer Graphics. New York, USA: ACM Press, 2001: 23-30.
( 0) 0)
|
| [11] |
ENRIGHT D, MARSCHNER S, FEDKIW R. Animation and rendering of complex water surfaces[J].
ACM Transactions on Graphics , 2002, 21 (3) : 736-744 ( 0) 0)
|
| [12] |
BARGTEIL A W, GOKTEKIN T G, O'BRIEN J F, et al. A semi-Lagrangian contouring method for fluid simulation[J].
ACM Transactions on Graphics , 2006, 25 (1) : 19-38 DOI:10.1145/1122501 ( 0) 0)
|
| [13] |
LOSASSO F, SHINAR T, SELLE A, et al. Multiple interacting liquids[J].
ACM Transactions on Graphics , 2006, 25 (3) : 812-819 DOI:10.1145/1141911 ( 0) 0)
|
| [14] |
ZHENG W, YONG J H, PAUL J C. Simulation of bubbles[J].
Graphical Models , 2009, 71 (6) : 229-239 DOI:10.1016/j.gmod.2009.08.001 ( 0) 0)
|
| [15] |
KIM B. Multi-Phase fluid simulations using regional level sets[J].
ACM Transactions on Graphics , 2010, 29 (6) : 175 ( 0) 0)
|
| [16] |
BROCHU T, BRIDSON R. Robust topological operations for dynamic explicit surfaces[J].
SIAM Journal on Scientific Computing , 2009, 31 (4) : 2472-2493 DOI:10.1137/080737617 ( 0) 0)
|
| [17] |
MVLLER M. Fast and robust tracking of fluid surfaces[C]//Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. New York, USA: ACM Press, 2009: 237-245.
( 0) 0)
|
| [18] |
WOJTAN C, THVREY N, GROSS M, et al. Deforming meshes that split and merge[J].
ACM Transactions on Graphics , 2009, 28 (3) : 1-10 ( 0) 0)
|
| [19] |
WOJTAN C, THVREY N, GROSS M, et al. Physics-inspired topology changes for thin fluid features[J].
ACM Transactions on Graphics , 2010, 29 (4) : 1-8 ( 0) 0)
|
| [20] |
DA F, BATTY C, WOJTAN C, et al. Double bubbles sans toil and trouble: discrete circulation-preserving vortex sheets for soap films and foams[J].
ACM Transactions on Graphics , 2015, 34 (4) : 1-9 ( 0) 0)
|



