2. 国网山东省电力公司, 山东 济南 250001
2. State Grid Shandong Electric Power Company, Jinan 250001, Shandong, China
当前, 风电已在全球范围内得到大规模开发。海上风况相对更加优良, 海上风电场不占用陆地资源, 同时往往距离沿海负荷中心更近, 使得海上风电近年来获得高度关注[1-3]。海上风电场采用众多的电力电子装置, 产生较高水平的复杂谐波[4-8]。采用海底电缆作为连接线, 引入的电容使得系统谐波以及谐振问题更加突出。受海浪等因素限制, 谐波适应性检测装置难以在风机近端开展相关并网测试, 需要引入一定距离的电缆在远端进行。受电缆的影响[9], 需要对测试条件做相应的修正。
文献[10]由多起风电场谐振脱网事故入手, 通过研究风电场系统不同位置的谐波含量及特点, 分析产生谐振的原因和相应的谐振机理, 并提出相应的治理方法和有针对性的谐波适应性检测方案。文献[11]重点关注了直驱风机所组成的风电场的谐波分布情况以及谐振相关问题。文献[12]对风电场中长距离电缆的分布电容做了详细介绍, 以海上风电场为对象, 探讨了长距离海底电缆对海上风电并网系统谐波以及谐振的影响。已有的研究主要侧重于风电场的谐波或者谐振问题[13-14], 对风电机组的电网适应性测试尚未见深入分析, 尤其是关于风电机组电网适应性远端测试方面, 尚缺乏深入讨论。
本研究重点分析了长距离电缆对谐波适应性测试的影响, 以空载条件为基准提出了基于电缆分布参数模型的海上风电机组谐波适应性远端检测方法。搭建了基于Simulink的DFIG并网模型, 分别比较了不同电缆长度、电容对风机谐振特性的影响。探讨了抑制谐波及避免谐振的方法。
1 海上风电场电气结构DFIG是当前主流的机型, 定子侧直接接入电网, 转子侧经变流器接入, 谐波问题比较复杂。
本研究以DFIG为研究对象, 风电场系统中主要包括风电机组、变压器、无功补偿装置和集电系统。国内风机出口电压通常为690 V, 经箱变升高到35 kV, 再由集电电缆并入汇流母线, 通过风电场升压站后接入电网。一般地, 在系统中压侧PCC处, 配置无功补偿装置。
2 风电机组谐波适应性检测 2.1 陆上风电机组近端测试方法2011年, 我国西北地区连续发生数起风机大规模故障跳闸停机事故, 促使国家电网公司对风电机组并网性能要求更加严格, 其中针对风电机组谐波适应性, 国家能源局制定并颁布了《风电机组电网适应性测试规程》(简称《测试规程》)。
根据《测试规程》, 利用谐波扰动发生装置分别产生2~25次测试谐波, 对风机电网谐波适应性进行测试, 具体测试内容如下:以电压总谐波畸变率考核, 利用谐波扰动发生装置设置奇、偶次谐波电压组合, 测试时间至少持续10 min; 利用测试装置设置奇次谐波含有率, 测试时间至少持续2 min; 利用测试装置设置偶次谐波含有率, 各次谐波下测试时间至少持续2 min。谐波扰动发生装置尽管结构不同, 但原理一致。通过采用电力电子变换技术, 利用AC/DC/AC将电网中的工频交流电压转变成扰动测试需要的谐波电压。
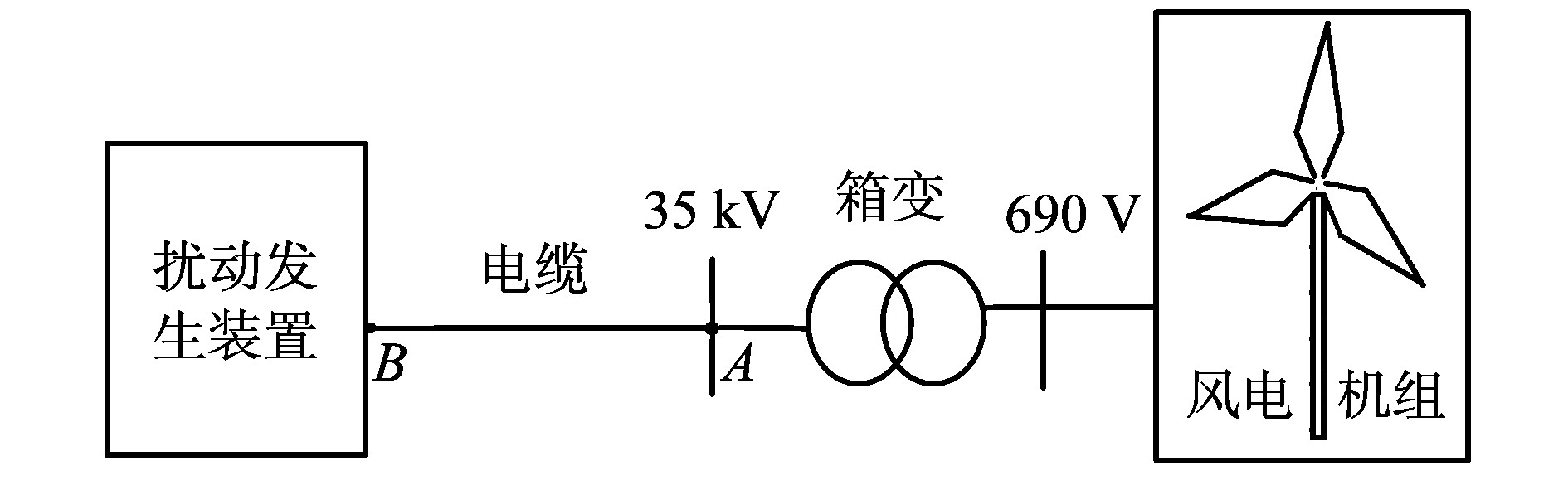
2.2 谐波适应性远端检测海上风浪情况比较复杂, 测试装置往往难以抵达风机电压出口处进行测量, 通常需要通过一定长度的电缆进行测试连接, 如图 1所示。因电缆分布电容较大, 给电网谐波适应性检测带来一定的影响, 需要对已有的近端测试方法进行改进。
|
图 1 远端检测系统结构示意图 Figure 1 Structure of the remote test system |
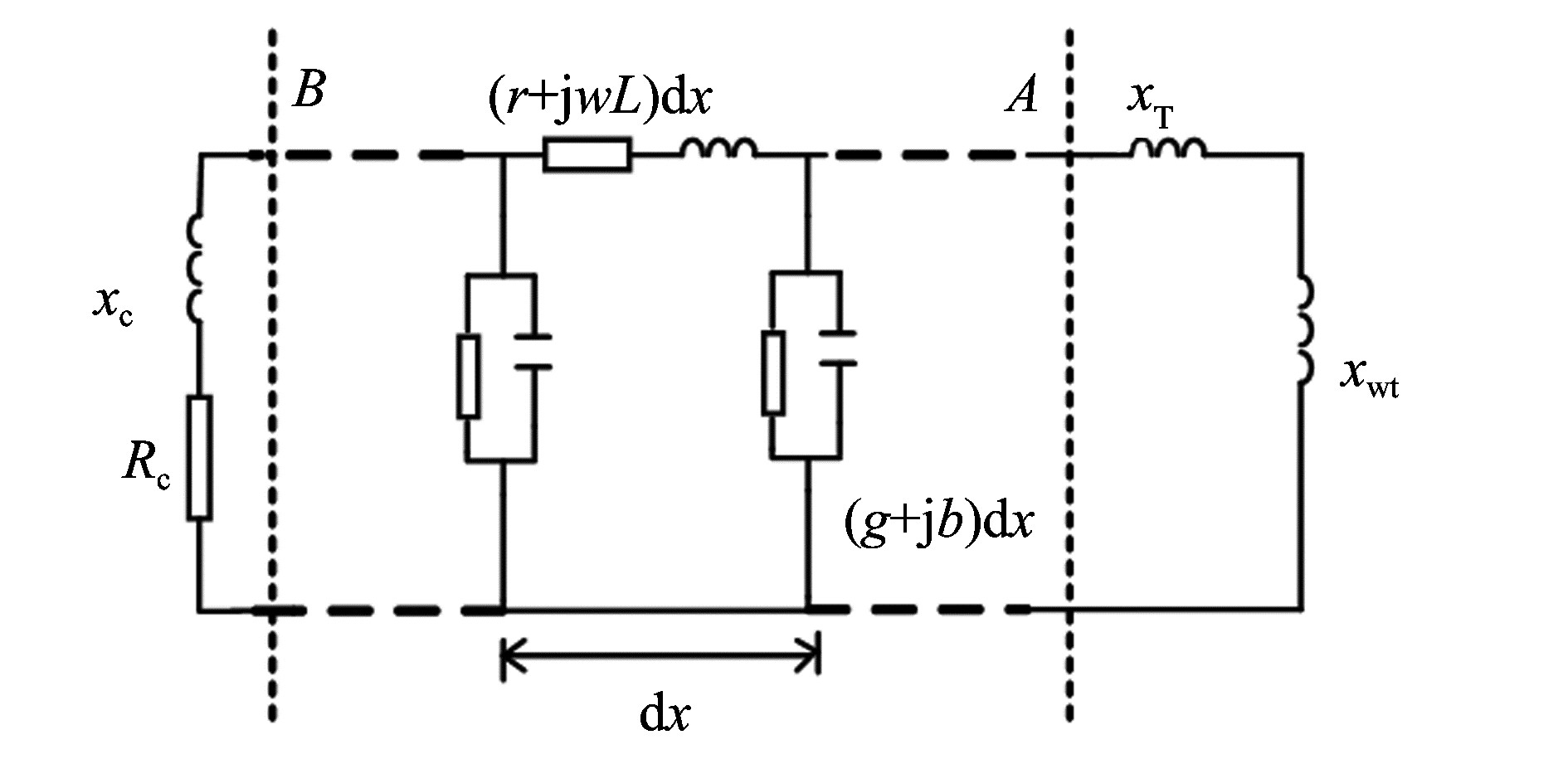
采用电缆的分布参数模型, 得到如图 2所示的等效测试电路。其中xc和Rc为测试装置的等效阻抗, A点为风机箱变中压侧出口端, B为远端检测点。AB段为海缆的分布参数等值电路, xt为海上风电机组箱变等值阻抗, xwt为风机的等值阻抗。电导g的值很小, 一般可以忽略。
|
图 2 等效测试电路图 Figure 2 The equivalent circuit of remote test system |
电缆采用分布参数模型表示如下:
| $ \begin{gathered} \frac{{{\text{d}}\dot V}}{{{\text{d}}x}} = \left( {r + {\text{j}}{w_f}L} \right)\dot I, \hfill \\ \frac{{{\text{d}}\dot I}}{{{\text{d}}x}} = \left( {g + {\text{j}}{w_f}C} \right)\dot V。 \hfill \\ \end{gathered} $ | (1) |
计算式(1)可以得到距离风机高压出口端A点x处位置的电压和电流的数值:
| $ \begin{gathered} V = {V_A}{\text{ch}}yx + {I_A}{Z_C}{\text{sh}}yx, \hfill \\ I = \frac{{{V_A}}}{{{\text{sh}}yx}} + {I_A}{\text{ch}}yx。 \hfill \\ \end{gathered} $ | (2) |
对于n次谐波, 则有:
| $ \begin{gathered} {y_n} = \sqrt {\left( {g + {\text{j}}n{w_1}C} \right)\left( {r + {\text{j}}n{w_1}L} \right)} , \hfill \\ {Z_{cn}} = \sqrt {\left( {r + {\text{j}}n{w_1}L} \right)/\left( {g + {\text{j}}n{w_1}C} \right)} 。 \hfill \\ \end{gathered} $ | (3) |
特别地, 空载时末端电流IA为零, 则可根据末端电压进行直接推算。谐波适应性检测时, 末端A点电压即为规程所要求测试电压。根据电缆模型, 结合实际引入的电缆参数, 通过计算或者仿真, 得到相应谐波电压的幅值放大比例Kn, 进而在远端B点对扰动发生装置生成的谐波电压幅值做对应的设定, 作为实际测试时的谐波电压输入值, 即VBn=VAn/Kn。其中VAn和VBn分别表示远端近端第n次谐波的相电压幅值。
3 电缆对风机谐振特性的影响 3.1 电缆长度对风电机组谐振特性的影响由于风电机组在风电场中所处的位置不同, 风机出口端到并网点的距离以及所引入集电电缆长度也不同, 进而所引入的电容、电感等相关电气参数也有所差别, 对测试系统以及正常工况下风机的运行有着不同的影响。风机和电缆参数分别如表 1和表 2所示。
| 表 1 2.5 MW双馈风机部分组件参数 Table 1 Parameters of some components of 2.5 MW DIFG |
| 表 2 35 kV不同电缆型号参数 Table 2 Parameters of different 35 kV submarine cables |
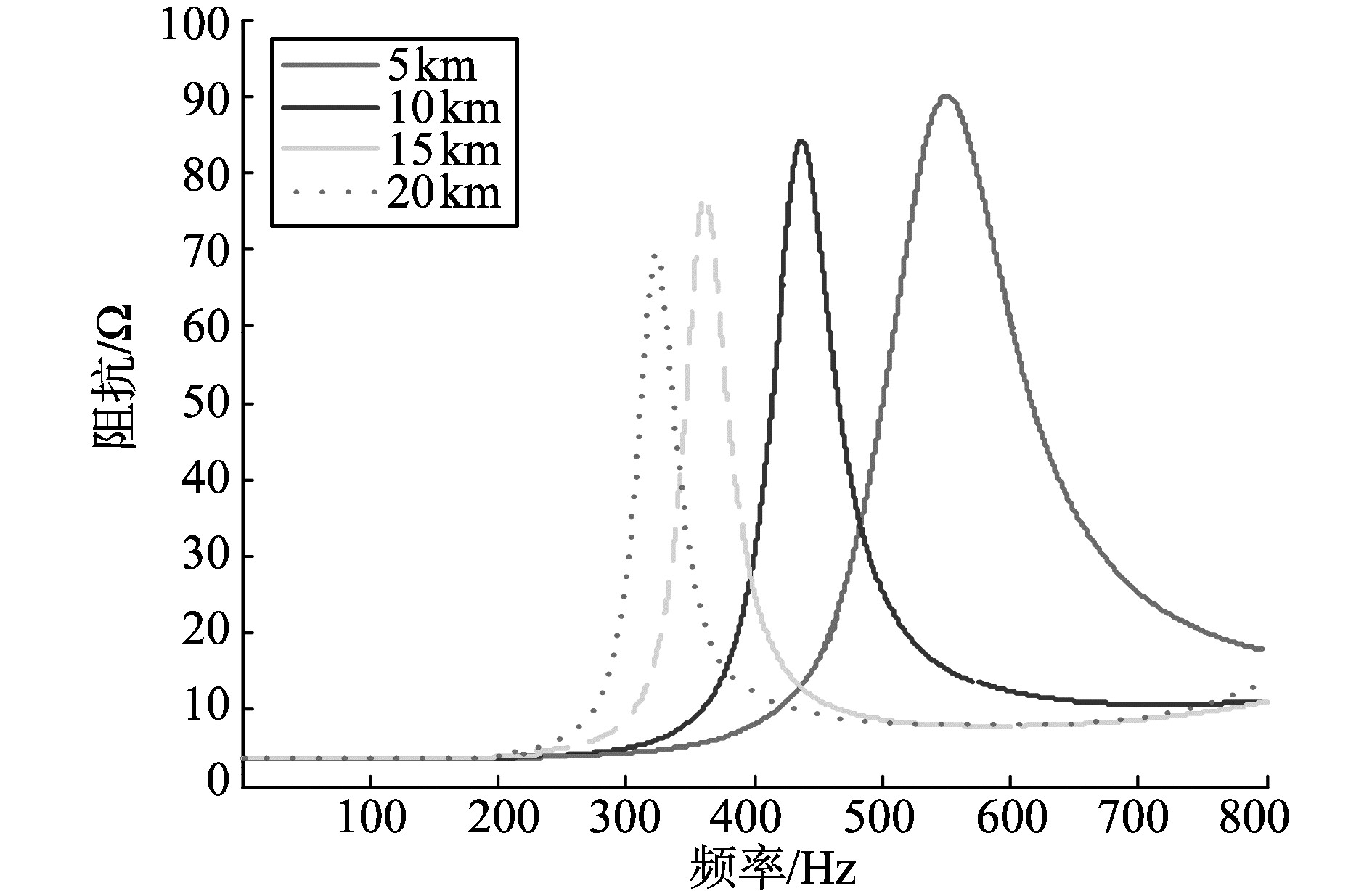
仿真中选用3×120型号的电缆, 分别设置长度为5、10、15以及20 km。图 3是不同电缆长度下系统的阻抗频率特性, 可以看出, 随着电缆长度的增加, 并网点处的谐振频率向低频方向偏移。采用5 km电缆时, 系统谐振频率约为550 Hz(11次谐波附近); 10 km电缆时对应的谐振频率约为440 Hz(9次谐波附近); 当电缆增加到20 km, 谐振频率进一步下降到约340 Hz(7次谐波附近)。同时还可以看出, 随着电缆长度增加, 发生谐振频率处的阻抗逐渐减少。
|
图 3 不同电缆长度下的阻抗频率特性 Figure 3 Resonant frequency with different cable lengths |
通过系统等值电路进行分析可知, 由于整个系统呈感性, 随着电缆长度增加, 引入的分布电容参数相应增大, 因此, 与系统中感性元件发生谐振的频率向更低方向偏移。
3.2 电缆电容参数对机组并网系统的谐振影响对于不同型号的电缆, 其单位长度内的分布电容等有所不同。为研究电缆电容电感参数对系统谐振特性的影响, 进一步采用如表 1中不同型号电缆做对比研究。
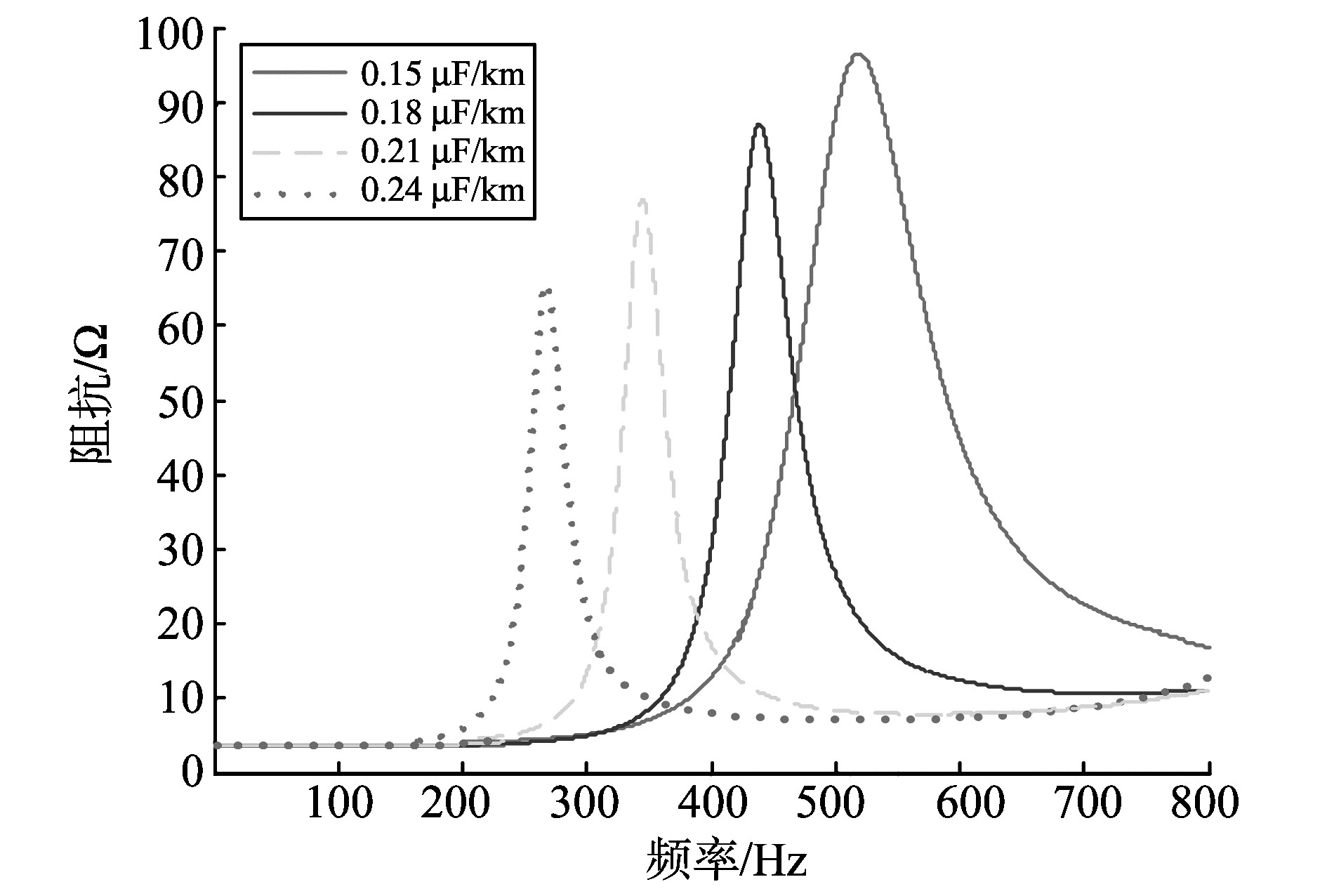
从表 2可以看出, 分布电容范围处于0.15~0.24 μF/km。为分析电缆电容对风机并网系统谐振特性的影响, 在研究时需要保持电阻及电抗的参数不变, 将电阻值设定为0.127 Ω/km, 将正序电抗值设定为0.133 Ω/km, 电缆长度设为10 km, 阻抗频率特性如图 4所示。从图 4可以看出, 随着电缆电容参数的增加, 系统谐振频率向低频方向偏移, 同时谐振阻抗不断减小。
|
图 4 不同电缆电容下谐振点变化 Figure 4 Resonance frequencies with different capacitances of cables |
以上分析表明, 由于大量使用电缆, 风机并网系统中存在着潜在谐振点。文献[15]指出, 全国范围内风电场谐振事故屡次发生, 造成风电机组大规模脱网, 严重影响电网的正常运行。谐波是谐振产生的必要因素[16-21], 采用滤波器能够抑制谐振谐波能够根本上避免谐振。本研究有针对性地提出了风机和风电场层面复合滤波的方法。
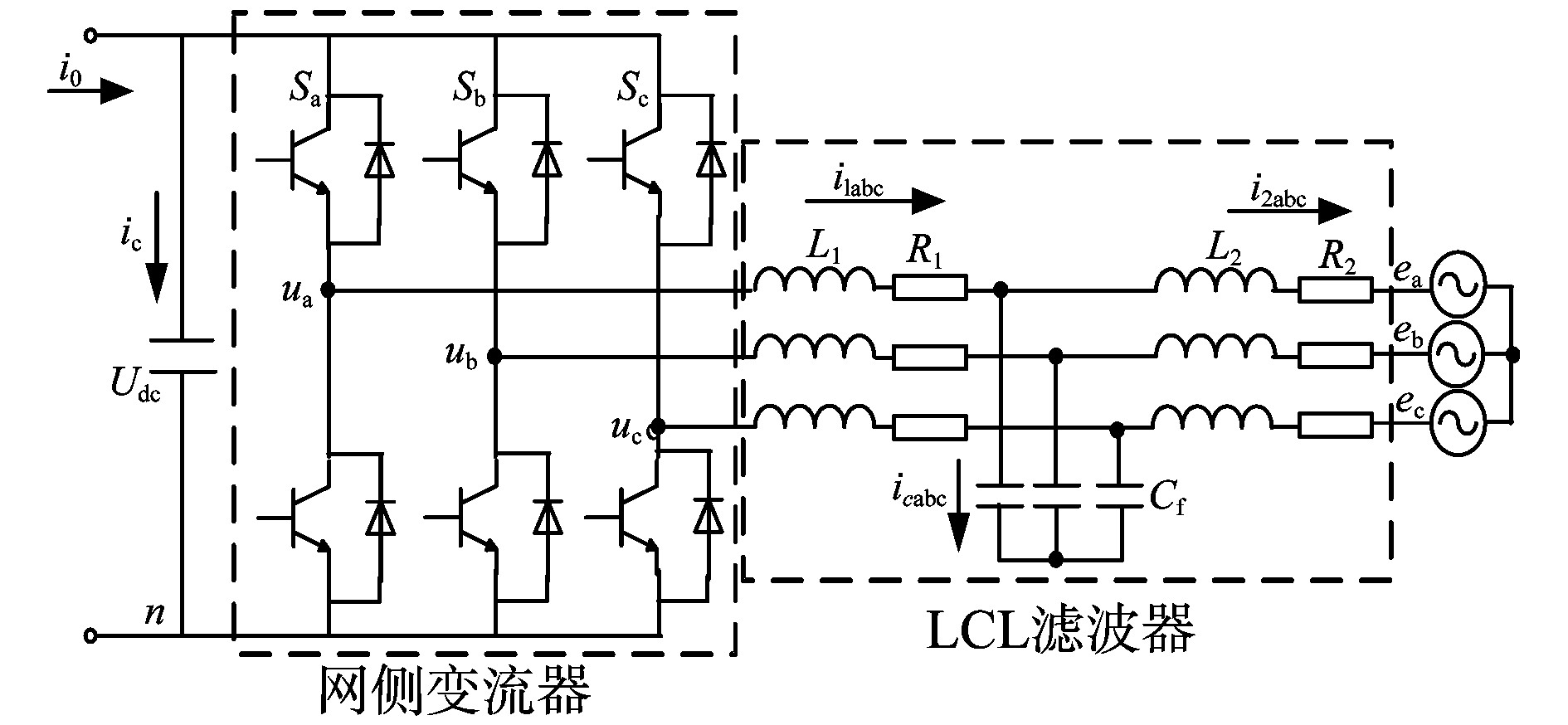
4.1 风电机组变流器LCL有源滤波器海上风况显著优于陆上, 采用大型的风机能增加风能的利用率。陆上风机功率一般在1~3 MW, 而海上风机功率可达5~10 MW, 甚至更大。LCL有源阻尼滤波器低能耗, 同时对高次谐波抑制效果突出, 适用于大型的海上风电机组。图 5是风电机组逆变侧并网结构示意图, 其中Udc是直流母线电压, 逆变器风机侧有电阻R1、电感L1, 网侧有电阻R2、电感Lf, 中间有“Y”型相连的Cf。
|
图 5 风机逆变侧并网结构图 Figure 5 Structure of wind turbine grid-connected inverters |
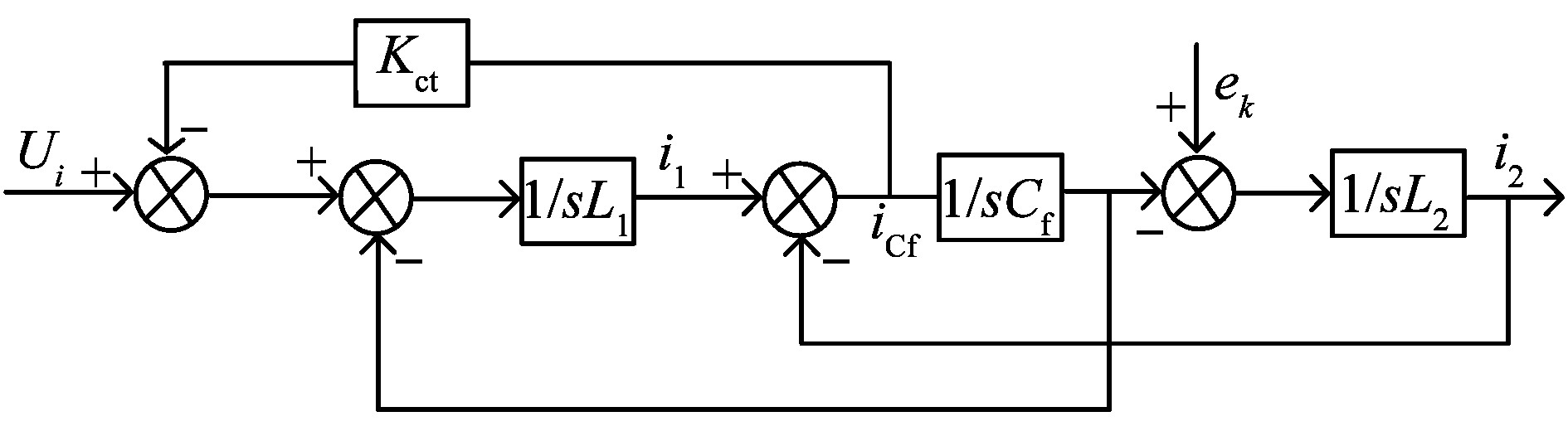
为避免LCL滤波器的无阻尼震荡, 可引入电容电流反馈实现有源阻尼控制, 控制框图如图 6所示, 其中Ui是控制电路输入电压, ek为并网点相电压(k为a, b, c相), KCf是电容电流反馈系数。
|
图 6 LCL有源阻尼滤波器控制框图 Figure 6 Control block of LCL active damping filter |
首先, 按照规定, 电感上的分压一般小于10%的电网线电压有效值。Lf可以参考传统单电感滤波器的设计。纹波电流一般限制为10%~25%, 这里取20%, 即:
| $ \frac{{{U_{{\text{dc}}}}}}{{8{f_{\text{s}}}{L_1}}} \leqslant 0.2{I_{1{\text{N}}}}, $ | (4) |
其中:I1N表示装置额定电流; fs表示PWM的开关频率; Udc表示直流母线电压。
同时, 为了提高对电流的追踪能力, LCL滤波器的电感上压降一般小于10%的电网线电压有效值。因此, 有以下约束:
| $ {L_1} \leqslant \frac{{\sqrt {{U_{{\text{dc}}}}/ - {U_{\text{m}}}} }}{{2\pi {f_1}{I_m}}} $ | (5) |
其中:f1是系统基波频率; Um和Im分别代表系统相电压和相电流的峰值。
考虑到滤波器的功率因数限制, 防止滤波器产生较大的无功输出, 通常设定Cf发出的无功功率小于变流器额定容量的5%[22], 则有:
| $ {C_{\text{f}}} \leqslant \frac{{{P_{\text{N}}}}}{{3 \times 2\pi {f_1}U_{\text{N}}^2}} \times 5\% , $ | (6) |
同时结合开关次谐波衰减比σ通常小于10%的要求[10], 则有:
| $ \sigma = \frac{{\text{1}}}{{|1 - w_{\text{s}}^2{L_2}{C_{\text{f}}}|}} \leqslant 10\% , $ | (7) |
其中ws为逆变器开关频率对应的角频率。滤波器系统阻尼系数为
| $ \xi = \frac{{{K_{{\text{cf}}}}}}{2} \times \sqrt {\frac{{{L_2}{C_{\text{f}}}}}{{{L_1}\left( {{L_1} + {L_2}} \right)}}} 。 $ | (8) |
根据实际需要, 可设定不同的阻尼系数, 本研究取0.707。可进一步确定反馈系数KCf的值。
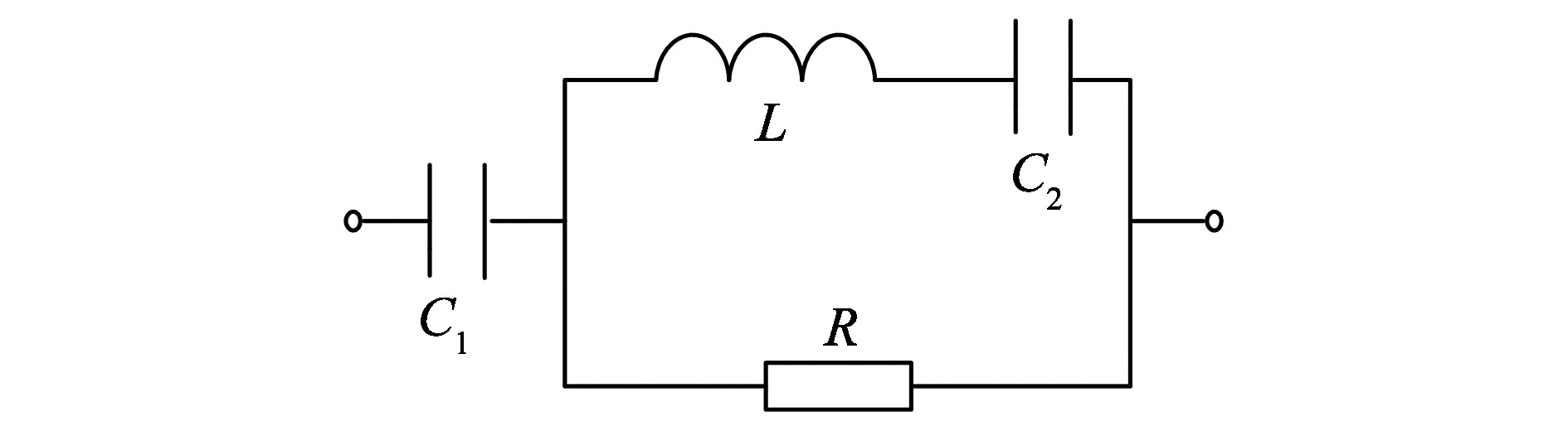
4.2 PCC处C型滤波对于大型海上风电场, 选择C型滤波器能够有效过滤系统内特定谐振谐波, 并对高频谐波有良好的抑制作用, 同时能够为系统提供无功补偿, 其结构如图 7所示, 包括电容C1和C2, 电感L以及电阻R。
|
图 7 C型滤波器典型结构 Figure 7 The typical configuration of the C-type filter |
在基波下, C1作为无功发生装置为系统提供电压支撑, 其值由系统所需无功补偿容量决定。
| $ {\omega _1} = \frac{1}{{\sqrt {L{C_2}} }}。 $ | (9) |
对于谐振谐波条件下, 当XL-XC1-XC2=0, 则有,
| $ {\omega _n} = \sqrt {\frac{{{C_1} + {C_2}}}{{L{C_1}{C_2}}}} . $ | (10) |
对于该次谐波, C型滤波器可等效为R-C串联电路, 此时的C型滤波器阻抗值最小。
| $ \frac{{{\omega _n}}}{{{\omega _1}}} = \sqrt {1 + {C_2}/{C_1}} , $ | (11) |
| $ |{Z_c}{|_{\min }} \approx 1/\left( {{n^2}\omega _1^2C_1^2R} \right). $ | (12) |
Zc可用来调节滤波器系统最小谐振阻抗, 保证滤波器安全稳定工作。设计时需要综合考虑。
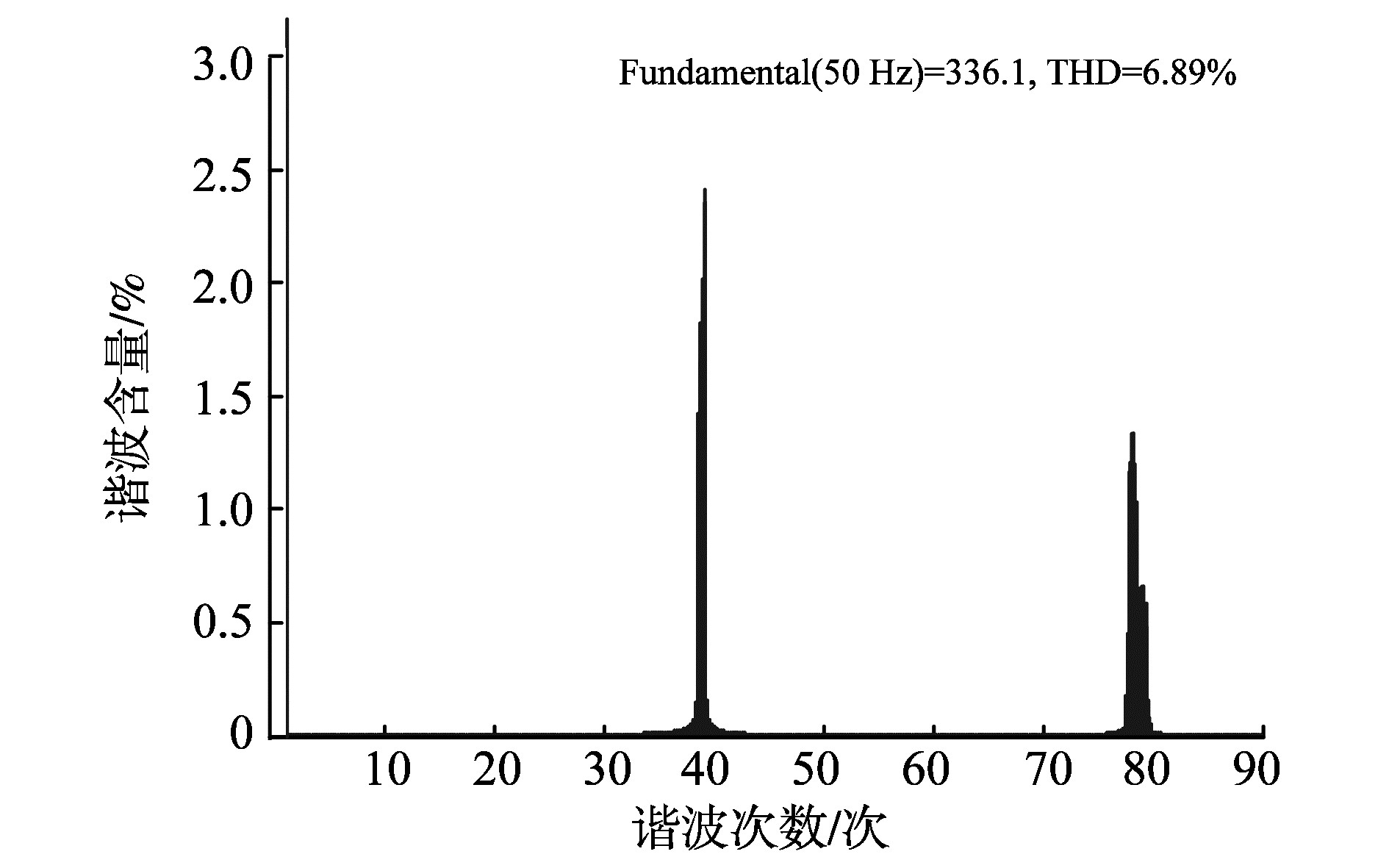
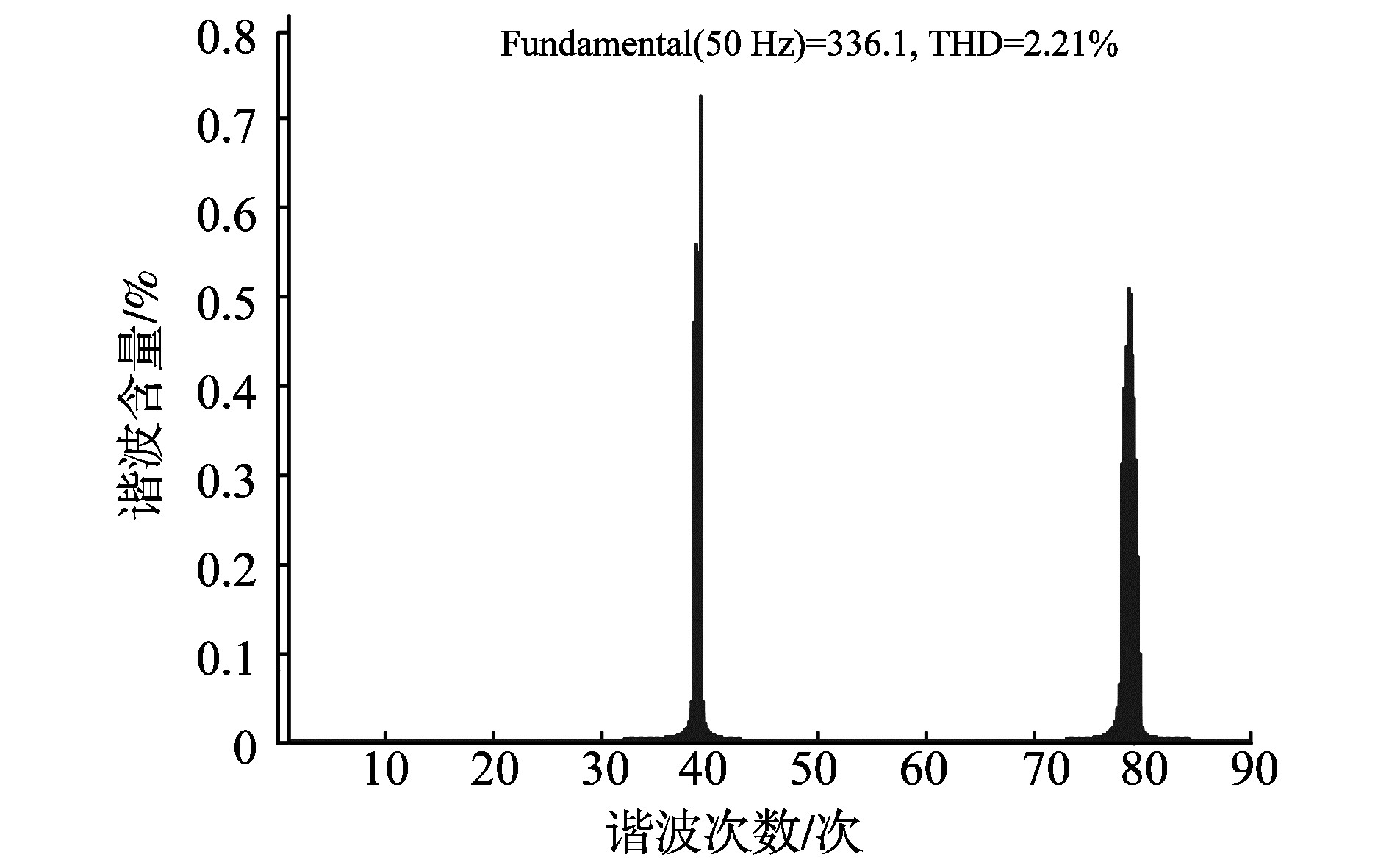
4.3 仿真算例根据表 2中的参数, 采用4.1设计方法, 可确定LCL有源阻尼滤波器的元件参数选择范围, 取L1为1.0 mH, Cf为150 μF, L2为0.5 mH, KCf为6.32。利用所设计的滤波器进行Simulink仿真, 并对谐波进行傅里叶分析。图 8和图 9分别是配置LCL滤波器前后风机逆变侧谐波成分。
|
图 8 未配置LCL滤波器时逆变侧并网谐波分析 Figure 8 Harmonic analysis with LCL active damping filter |
|
图 9 LCL有源阻尼滤波器配置后的谐波分析 Figure 9 Harmonic analysis with LCL active damping filter |
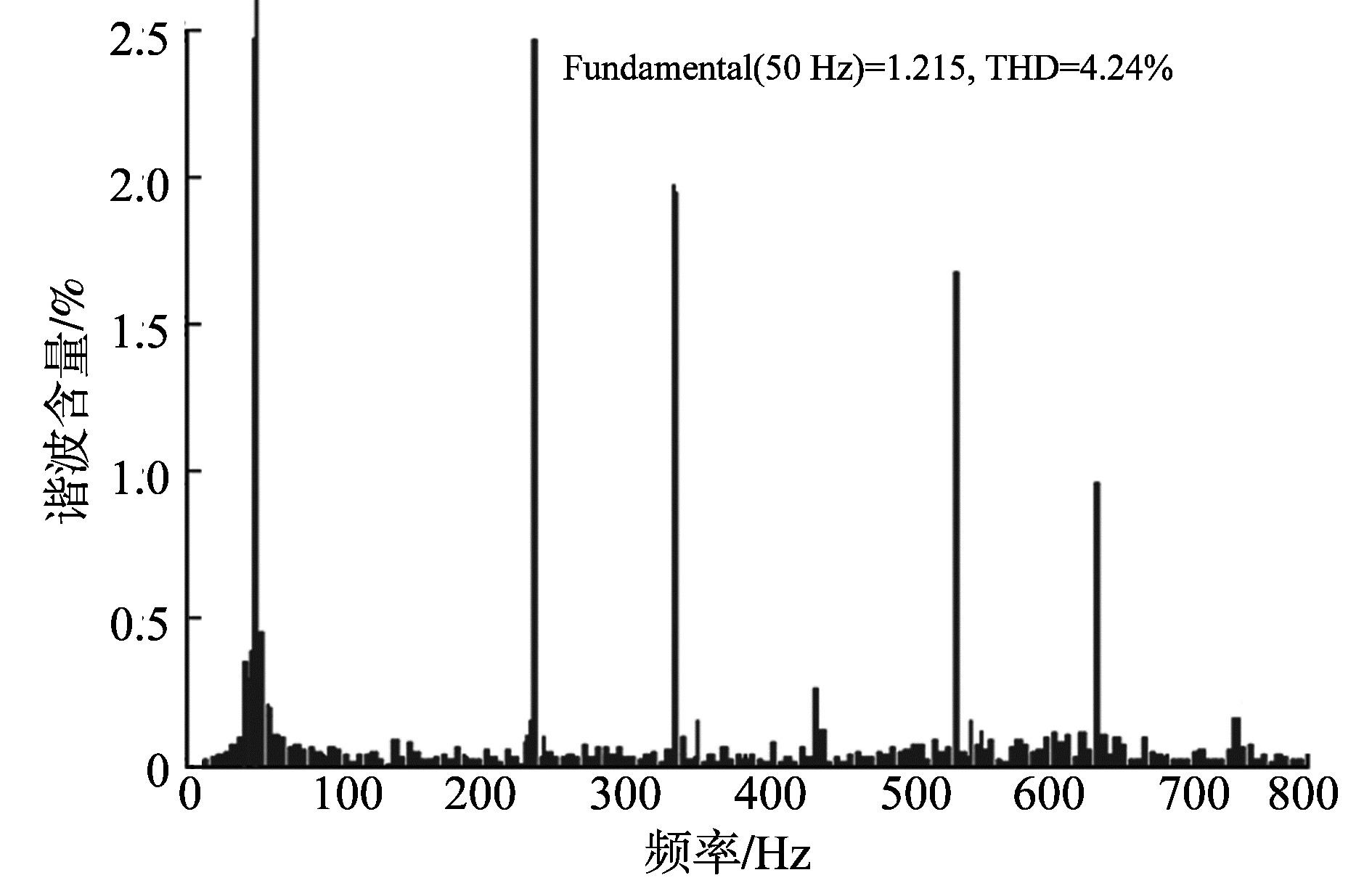
图 8和图 9表明, 配置有源滤波器能够有效抑制DFIG逆变器注入电网的高次谐波, 降低风机注入电网中的谐波。图 9和图 10分别反映了配置C型滤波器前后PCC处的谐波清洁。
|
图 10 PCC处未配置C型滤波器的谐波分析 Figure 10 Harmonic analysis at PCC without C-type filiter |
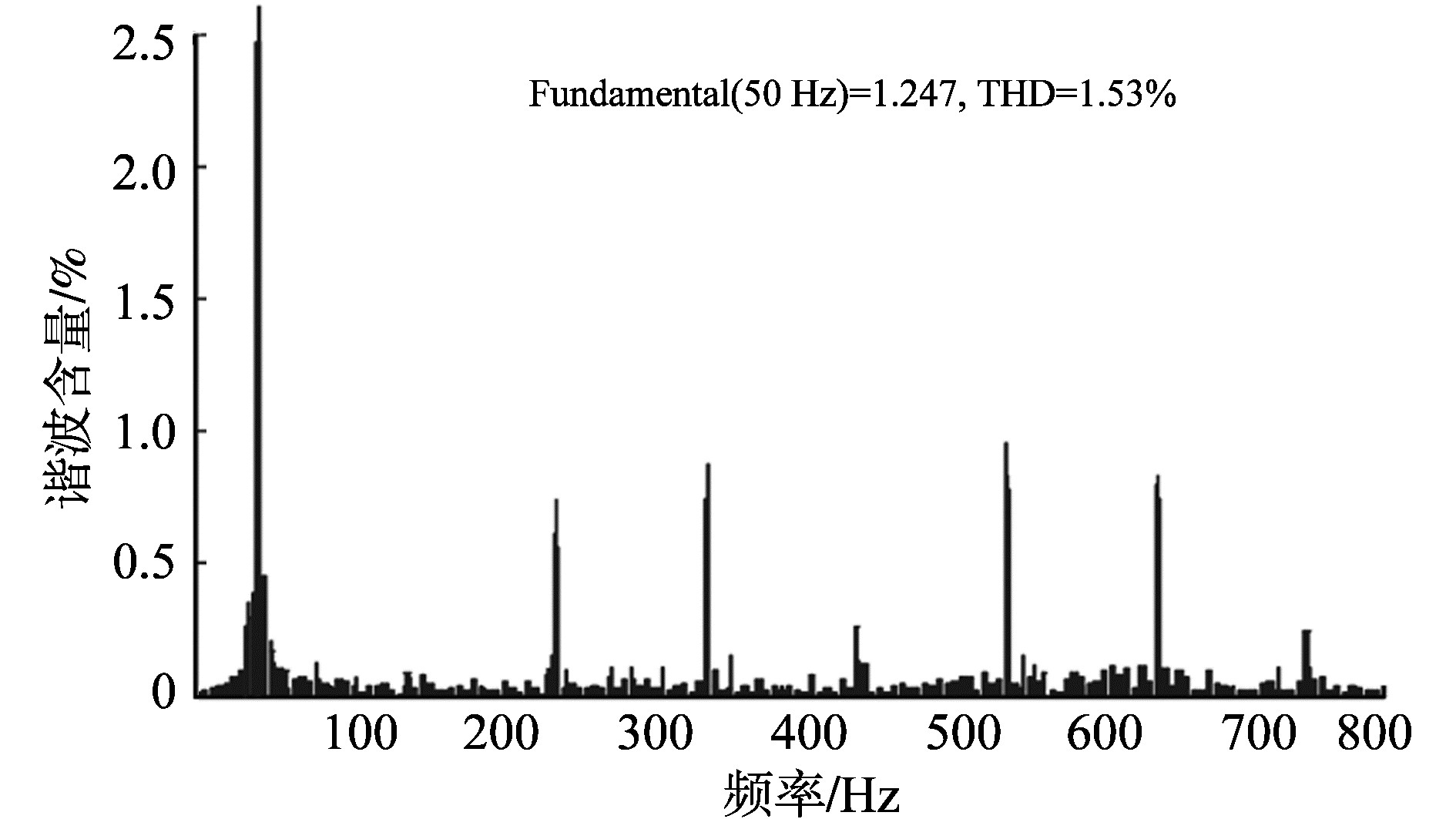
采用5×5的风场布局时, PCC配置20MVar无功补偿, 系统会在5次谐波附近发生谐振。根据4.2中的方法可确定C型滤波器各个元件的参数。C1的选值为17 μF, C2约为400 μF, 电感L约为25 mH。综合考虑系统谐波下的能耗以及滤波器的安全可靠性, 选取R的值为100 Ω。分析图 10和图 11可知, 配置所设计的C型滤波器后, 能够显著降低谐振谐波含量, 同时对其他高次谐波有一定抑制作用。
|
图 11 PCC处配置C型滤波器后的谐波分析 Figure 11 Harmonic analysis at PCC with C-type filiter |
本研究首次提出了基于电缆分布参数模型的海上风电机组谐波适应性远端检测方法。分析了不同电缆长度和电容参数对风机谐振特性的影响, 研究表明, 更长距离的电缆, 电容参数越大型号的电缆会使得风机的谐振越低、谐振阻抗越小。为避免谐振, 探索出了一种复合滤波方法, 通过对DFIG机组配置LCL有源阻尼滤波器降低高次谐波, 并在风电场PCC配置C型滤波器, 为系统提供无功补偿的同时, 实现对谐振谐波的抑制, 最后利用Simulink仿真证明了该方法的有效性。本研究为海上风机谐波适应性并网检测提供可行的理论思路, 并可为抑制海上风电场谐波谐振提供有效的滤波方案。
| [1] |
ERLICH I, SHEWAREGA F, FELTES C, et al. Offshore wind power generation technologies[J].
Proceedings of the IEEE , 2013, 101 (4) : 891-905 DOI:10.1109/JPROC.2012.2225591 ( 0) 0)
|
| [2] |
SERRANO G J, BURGOS P M, RIQUELME S J. A new and efficient method for optimal design of large offshore wind power plants[J].
IEEE Transactions on Power Systems , 2013, 28 (3) : 3075-3084 DOI:10.1109/TPWRS.2013.2251014 ( 0) 0)
|
| [3] |
王锡凡, 卫晓辉, 宁联辉, 等. 海上风电并网与输送方案比较[J].
中国电机工程学报 , 2014, 34 (31) : 5459-5466 WANG Xifan, WEI Xiaohui, NING Lianhui, et al. Integration techniques and transmission schemes for off-shore wind farms[J]. Proceedings of the CSEE , 2014, 34 (31) : 5459-5466 (  0) 0)
|
| [4] |
CHAVEZ-BAEZ M V, ANAYA-LARA O, LO K L, et al. Review of harmonics in offshore wind farms[C]//2013 48th International Universities Power Engineering Conference. Dublin, Ireland: IEEE Press, 2013:1-5.
( 0) 0)
|
| [5] |
PETERSSON A, THIRINGER T, HARNEFORS L, et al. Modeling and experimental verification of grid interaction of a DFIG wind turbine[J].
IEEE Transactions on Energy Conversion , 2006, 4 (4) : 878-886 ( 0) 0)
|
| [6] |
ZHI D, XU L. Direct power control of DFIG with constant switching frequency and improved transient performance[J].
IEEE Transactions on Energy Conversion , 2007, 22 (1) : 110-118 DOI:10.1109/TEC.2006.889549 ( 0) 0)
|
| [7] |
EGEA-ALVAREZ A, BIANCHI F, JUNYENT-FERRE A, et al. Voltage control of multiterminal VSC-HVDC transmission systems for offshore wind power plants: design and implementation in a scaled platform[J].
IEEE Transactions on Industrial Electronics , 2013, 60 (6) : 2381-2391 DOI:10.1109/TIE.2012.2230597 ( 0) 0)
|
| [8] |
ZUBIAGA M, ABAD G, BARRENA J A, et al. Spectral analysis of a transmission system based on AC submarine cables for an offshore wind farm[C]//Industrial Electronics, 35th Annual Conference of IEEE. Porto, Portugal: IEEE Press, 2009:871-876.
( 0) 0)
|
| [9] |
周栾爱, 唐文左, 崔晓华, 等. 电力电缆运行安全非线性模糊综合评判模型[J].
山东大学学报(工学版) , 2013 (6) : 83-88 ZHOU Luanai, TANG Wenzuo, CUI Xiaohua, et al. Nomlinear fuzzy synthetic evaluation model for operating condition of power cables in tunnels[J]. Journal of Shandong University(Engineering Science) , 2013 (6) : 83-88 (  0) 0)
|
| [10] |
樊熠, 张金平, 谢健, 等. 风电场谐波谐振测试与分析[J].
电力系统自动化 , 2016, 40 (2) : 147-151 FAN Yi, ZHANG Jinping, XIE Jian, et al. Testing and analysis for harmonic resonance of wind farm[J]. Automation of Electric Power Systems , 2016, 40 (2) : 147-151 (  0) 0)
|
| [12] |
米富丽.直驱型风电系统谐波与谐振研究[D].哈尔滨:哈尔滨工业大学, 2013.
MI Fuli. Research on harmonics and reasonance for direct-drive wind power system[D]. Harbin: Harbin Institute of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014001536.htm (  0) 0)
|
| [13] |
SHAO Z, SHUAI J, XI L, et al. Resonance issues and damping techniques for grid-connected inverters with long transmission cable[J].
IEEE Transactions on Power Electronics , 2014, 29 (1) : 110-120 DOI:10.1109/TPEL.2013.2253127 ( 0) 0)
|
| [14] |
贺益康, 徐海亮. 双馈风电机组电网适应性问题及其谐振控制解决方案[J].
中国电机工程学报 , 2014, 34 (29) : 5188-5203 HE Yikang, XU Hailiang. The grid adaptability problem of DFIG-based wind turbines and its solution by resonant control scheme[J]. Proceedings of the CSEE , 2014, 34 (29) : 5188-5203 (  0) 0)
|
| [15] |
ZHANG S, JIANG S, LU X, et al. Resonance issues and damping techniques for grid-connected inverters with long transmission cable[J].
IEEE Transactions on Power Electronics , 2014, 29 (1) : 110-120 DOI:10.1109/TPEL.2013.2253127 ( 0) 0)
|
| [16] |
李少林, 王瑞明, 陈晨, 等. 大容量永磁同步风电机组系统谐振分析与试验研究[J].
可再生能源 , 2014, 32 (9) : 1288-1293 LI Shaolin, WANG Ruiming, CHEN Chen, et al. Analysis and experiment research on resonance characteristics of large-capacity permanent magnet synchronous generator system[J]. Renewable Energy Resources , 2014, 32 (9) : 1288-1293 (  0) 0)
|
| [17] |
KING R, EKANAYAKE J B. Harmonic modelling of offshore wind farms[C]//Power and Energy Society General Meeting. Minnesota, USA:IEEE Press, 2010:1-6.
( 0) 0)
|
| [18] |
GHASSEMI F, KOO K. Equivalent network for wind farm harmonic assessments[J].
IEEE Transactions on Power Delivery , 2010, 25 (3) : 1808-1815 DOI:10.1109/TPWRD.2009.2037909 ( 0) 0)
|
| [19] |
SHAFIU A, HERNANDEZ A, SCHETTLER F, et al. Harmonic studies for offshore windfarms[C]//9th IET International Conference on AC and DC Power Transmission. London, UK:IET Digital Library, 2010:41-41.
( 0) 0)
|
| [20] |
LI J, SAMAAN N, WILLIAMS S. Modeling of large wind farm systems for dynamic and harmonics analysis[C]// Transmission and Distribution Conference and Exposition. [S.l.]:IEEE Press, 2008:326-332.
( 0) 0)
|
| [21] |
GHOSHAL A, JOHN V. Active damping of LCL filter at low switching to resonance frequency ratio[J].
IEEE Transactions on Power Electronics , 2015, 8 (4) : 574-582 DOI:10.1049/iet-pel.2014.0355 ( 0) 0)
|
| [22] |
王盼, 刘飞, 查晓明. 基于有源阻尼的并联有源滤波器输出LCL滤波器设计[J].
电力自动化设备 , 2013, 32 (4) : 161-166 WANG Pan, LIU Fei, ZHA Xiaoming. Design of output LCL filter based on shunt APF with active damping[J]. Electric Power Automation Equipment , 2013, 32 (4) : 161-166 (  0) 0)
|




