2. 国网山东省电力公司, 山东 济南 250001;
3. 国网山东省电力公司电力科学研究院, 山东 济南 250002
2. State Grid Shandong Electric Power Company, Jinan 250001, Shandong, China ;
3. Electric Power Research Institute, State Grid Shandong Electric Power Company, Jinan 250002, Shandong, China
随着全球能源互联网[1]概念的提出, 我国国内电网建成坚强统一的特高压网架的进程不断加快, 目前, 我国已建成3条特高压交流输电通道[2]。特高压交流输电工程的建设在加强电网结构、提高电网输电能力的同时, 也引起了受端电网的一系列的安全稳定问题, 短路电流超标就是其中较为严重的一个问题。
为解决受端电网的短路电流超标问题, 国内外电网都采取了许多针对性的限流方案[3-7]。这些限流方案一般从电网结构调整角度入手, 通过采用一种或者几种限流措施的优化组合将短路电流控制在容许的范围内。文献[8]提出了一种基于开断线路灵敏度的网架结构调整方法, 既能实现较好的限流效果, 又能尽量保持网架结构的完整性。文献[9]则针对超导故障限流器的安装位置、数量以及阻抗值, 提出了一种基于NSGA-II算法的故障限流器优化配置方法。对于短路超标不太严重的情况, 仅采用一种限流措施的优化配置即可实现短路电流的有效控制。但如果短路电流超标严重或者电网的实际运行状况十分复杂, 就必须要采取多种限流的优化组合。文献[10]在分析了多种常用限流措施的限流效果和经济性的基础上, 提出了多种限流措施的综合优化配置方法。采用变量0和1模拟各种限流措施的投运与否, 采用整数变量模拟限流电抗器、故障限流器以及高阻抗变压器的容量, 将限流措施的优化配置问题归纳为一个混合整数规划问题。文献[11]在文献[10]的基础上, 考虑了潮流约束对限流措施优化配置的影响, 以经济性最优为目标建立了限流措施优化配置的数学模型, 并采用改进的离散粒子群算法进行求解。目前, 限流措施的综合优化配置往往仅考虑三相短路电流的控制, 而没有对单相短路电流提出明确的限流目标和限流方法。
本研究针对实际特高压受端电网中单相短路电流不断升高甚至超过三相短路电流的情况, 分析了其产生的原因, 并给出了专门的限流措施。对各种限流措施的限流灵敏度和经济性进行了统一描述, 并给出了限流措施配置对象的对象灵敏度的定义, 并基于此对限流措施配置对象进行筛选。以限流方案的经济性和电网结构紧密性为目标函数, 以单相短路电流和三相短路电流同时满足要求为主要约束条件, 建立了特高压受端电网的综合限流优化模型, 采用自适应混合PSO算法对该优化模型进行求解。以济宁地区规划电网为例, 验证了所提限流优化方法的有效性。
1 单相短路电流超标原因及其专门限制措施在特高压受端电网中, 单相短路电流超过三相短路电流, 甚至超过断路器遮断容量的情况时有发生[12]。可从短路电流的计算出发, 分析这一现象产生的原因。单相短路电流和三相短路电流
| $ \begin{gathered} {{\dot I}_{{\text{f}},0}} = {{\dot I}_{{\text{fa}}\left( 1 \right)}} + {{\dot I}_{{\text{fa}}\left( 2 \right)}} + {{\dot I}_{{\text{fa}}\left( 0 \right)}} = 3{{\dot I}_{{\text{fa}}\left( 1 \right)}} = \hfill \\ \frac{{3\dot V_{\text{f}}^0}}{{{Z_{{\text{ff}}\left( 1 \right)}} + {Z_{{\text{ff}}\left( 2 \right)}} + {Z_{{\text{ff}}\left( 0 \right)}}}}, \hfill \\ {{\dot I}_{{\text{f}},1}} = \frac{{\dot V_{\text{f}}^0}}{{{Z_{{\text{ff}}}}}}, \hfill \\ \end{gathered} $ | (1) |
式中:
一般来说, 正序阻抗和负序阻抗都与电源点与短路点之间的电气距离有关, 且有Zff(1)≈Zff(2); 而零序阻抗则与中性点的接地方式有关。结合式(1)可知, 单相短路电流和三相短路电流的根本差异在于零序阻抗。电力系统的零序网络主要由输电线路和变压器的零序阻抗组成。在出现单相短路电流升高的地区, 一方面, 其电网网架结构往往比较密集, 输电线路的平均长度较短, 输电线路提供的零序阻抗不大; 另一方面, 这些地区都配置了大量的自耦降压变压器以满足下送功率的需要, 自耦变压器正常运行时其中性点必须有效接地, 这就导致了多条零序接地支路并联的情况, 引起系统等效零序阻抗的降低。对于一个短路点而言, 零序网络中的接地支路越多, 并联的零序阻抗值就越小, 总的零序阻抗就越接近甚至小于总的正序阻抗, 从而导致单相短路电流逐渐升高甚至超过三相短路电流。综上分析, 大量自耦变压器的使用, 正是导致单相短路电流升高的具体原因。
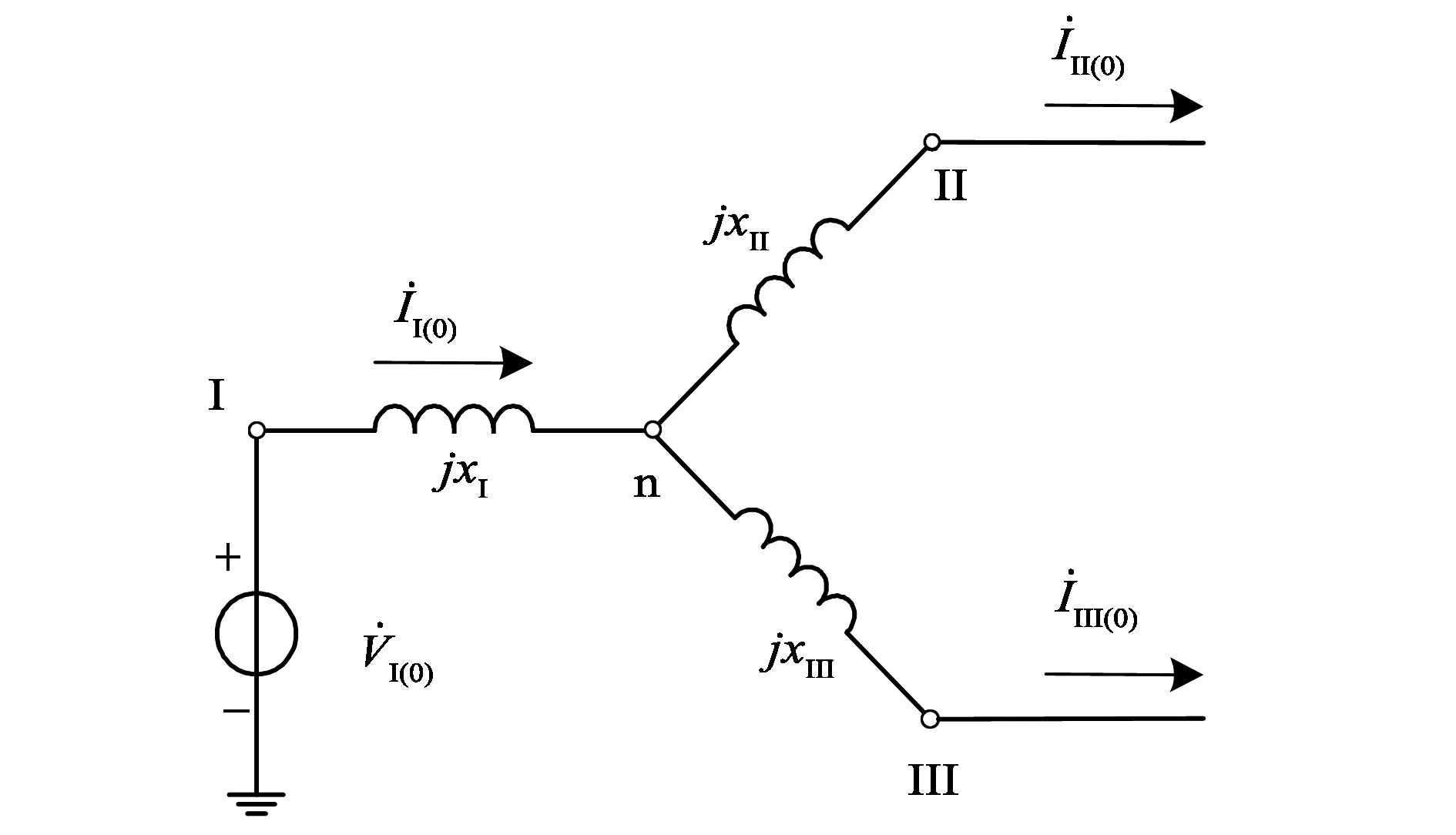
由于自耦变压器在我国特高压电网建设中的应用前景[1], 将其替换为非自耦变压器是不现实的, 而为了限制单相短路电流, 可以采取在自耦变压器中性点加装接地电抗的措施[13-15]。三绕组自耦变压器直接接地的零序等值电路如图 1所示。在形成等值电路时, 三绕组变压器转化为3个等效两绕组变压器处理, xⅠ、xⅡ和xⅢ分别为三绕组自耦变压器3个绕组(即3个等效两绕组变压器)的等效零序电抗。
|
图 1 三绕组自耦变压器直接接地的零序等值电路 Figure 1 Zero-sequence equivalent circuit of directly-grounded three-winding autotransformer |
自耦变压器中性点加装接地电抗xn后的零序等值参数可以通过3次短路试验计算[16]得到
| $ \left\{ \begin{gathered} {{x'}_Ⅰ} = {x_Ⅰ} + 3{x_n}\left( {1 - {k_{12}}} \right), \hfill \\ {{x'}_Ⅱ} = {x_Ⅱ} + 3{x_n}\left( {{k_{12}} - 1} \right){k_{12}}, \hfill \\ {{x'}_Ⅲ} = {x_Ⅲ} + 3{x_n}{k_{12}}. \hfill \\ \end{gathered} \right. $ | (2) |
式中:x′Ⅰ、x′Ⅱ和x′Ⅲ分别为加装接地电抗后对应3个绕组的等效零序电抗。可见, 三绕组自耦变压器中性点加装小电抗后, 3个绕组的等效零序电抗都发生了变化, 这相当于在零序等值网络中的对应3条支路上同时加装串联电抗, 各串联电抗的阻抗值由式(2)决定。
2 限流措施的分析与限流措施配置对象的筛选 2.1 限流措施的灵敏度和经济性本研究的通用限流措施包括开断线路、母线分段运行、线路出串、加装线路串联电抗器和换用高阻抗变压器, 专用的单相限流措施为变压器中性点加装接地电抗。结合以往的研究[7, 17-19]和前文的分析可知, 这些限流措施对超标站点三相短路电流和单相短路电流的限制作用, 都是通过改变相应序别等值网络中某些支路的阻抗值, 进而改变超标站点的节点自阻抗来实现的[20], 因此它们的限流效果都可以用超标站点k相应序别自阻抗变化的灵敏度
| $ {\alpha _k} = {\tau _{k,1}}\frac{{{{Z'}_{kk,1}} - {Z_{kk,1}}}}{{{Z_{kk,1}}}} + {\tau _{k,0}}\frac{{{{Z'}_{kk,0}} - {Z_{kk,0}}}}{{{Z_{kk,0}}}}, $ | (3) |
式中:Zkk, 1、Zkk, 0和Z′kk, 1、Z′kk, 0分别为限流措施采取前后超标站点的正序和零序自阻抗;τk, 1和τk, 0分别为表示三相短路电流和单相短路电流是否超标的量, 若相应短路电流超标, 其值取为1, 否则, 其值取为0。αk的值越大, 说明该限流措施对超标站点k的正序和零序自阻抗增大的影响越大, 即限制三相短路电流和单相短路电流的效果越好。
实际电网中, 限流效果往往不是关注某一站点短路电流的降低, 而是考虑某一具体限流措施实施后对所有超标站点的综合限流效果[5]。因此, 定义某一限流措施的加权限流灵敏度
| $ \alpha = \sum\limits_{k = 1}^{Ne} {\left( {{\omega _{k,1}}\frac{{{{Z'}_{kk,1}} - {Z_{kk,1}}}}{{{Z_{kk,1}}}} + {\omega _{k,0}}\frac{{{{Z'}_{kk,0}} - {Z_{kk,0}}}}{{{Z_{kk,0}}}}} \right),} $ | (4) |
式中:Ne为超标站点的总数;ωk, 1和ωk, 0分别为该限流措施对站点k的正序自阻抗灵敏度加权系数和零序自阻抗灵敏度加权系数, 定义为
| $ {\omega _{k,1}} = {\tau _{k,1}}\left( {\frac{{{I_{k,1}}}}{{I_k^{{\text{break}}}}} - 1} \right),{\omega _{k,0}} = {\tau _{k,0}}\left( {\frac{{{I_{k,0}}}}{{I_k^{{\text{break}}}}} - 1} \right) $ | (5) |
式中:Ik, 1和Ik, 0分别为超标站点k的三相短路电流和单相短路电流;Ikbreak为站点k的断路器遮断电流。加权系数表示站点k在限流措施采取前的超标程度, 因此, 式(4)定义的加权限流灵敏度不仅考虑了限流效果的绝对程度, 也考虑了站点自身的超标程度, 更全面地体现了限流措施的整体效果。加权限流灵敏度越大, 说明该限流措施实施后, 各超标站点的短路电流下降越多, 整体限流效果越好。
各种限流措施的应用不仅要考虑其限流效果, 还要考虑应用该限流措施的经济成本, 限流措施的成本函数
| $ c = {k_{as}} + {k_{bs}}{z_s} $ | (6) |
式中:kas和kbs为经济成本系数, 对于不同的限流措施可以取不同的常数值。zs为可以理解为限流装置的参数值, 对于不同的限流措施其具体含义是不相同的, 对于开断线路、母线分段和线路出串, zs=0;对于加装线路串联电抗的措施, zs为串联电抗的阻值; 对于换用高阻抗变压器的措施, zs为变压器短路电抗的增量; 对于加装中性点小电抗的措施, zs为中性点阻抗的阻抗值。考虑到设备制造和选型的实际情况, zs通常不能连续取值, 它是一个离散的量。
2.2 限流措施配置对象的筛选对各种限流措施进行分析可知, 开断线路和加装线路串联电抗器是以线路为配置对象的限流措施, 母线分段运行和线路出串从等效的角度都可以看作是对母线的操作, 而换用高阻抗变压器和变压器中性点加装接地电抗则以变压器为配置对象。一般来说, 电力系统中限流措施配置对象的总量是很庞大的, 如果将所有的配置对象都加入到限流方案寻优的候选集合中去, 那么组合形成的候选限流方案的数量必然会急剧增加甚至造成维数灾, 导致寻优速度过于缓慢, 可能无法得到最优解。因此, 合理的处理方法是采取一定的筛选策略, 只将配置限流措施后限流效果较好的配置对象加入到寻优集合中去。
由2.1节分析可知, 具体限流措施的限流效果用加权限流灵敏度来表示, 类似地, 也可以对限流措施的配置对象定义对象灵敏度
| $ {\delta _i} = \frac{1}{N}\sum\limits_{k = 1}^N {{\alpha ^{\left( {i,k} \right)}}} , $ | (7) |
式中:N为限流措施配置对象i可用限流措施的数目, 且N≤2;α(i, k)为配置对象i在配置可用限流措施k后的加权限流灵敏度。
基于式(7)定义的对象灵敏度, 筛选限流措施配置对象的步骤具体为:首先, 对可以进行限流措施配置的线路、母线和变压器支路分别进行对象灵敏度的计算; 然后, 对3种配置对象分别按照综合限流灵敏度的降序排列; 最后, 选择前Nl回线路、前Nb条母线和前Nt条变压器支路加入决策变量。需要注意的是, Nl、Nb和Nt的选取大小要合适, 如果过大会增加计算量, 甚至造成维数灾, 起不到筛选应有的作用; 如果过小, 则可能找不到最优解。
3 考虑单相短路电流限制的综合限流优化 3.1 数学模型综合限流优化不仅要使系统的单相短路电流和三相短路电流都不超过控制上限, 潮流和设备参数在合理的范围内, 还要求总的投资成本最低。因此, 经济性是综合限流优化的重要目标函数, 结合2.1节中对各种限流措施经济性的分析, 定义限流方案的经济性目标函数为
| $ \min {f_1} = \sum\limits_{s = 1}^{{N_s}} {{u_s}\left( {{k_{as}} + {k_{bs}}{z_s}} \right)} , $ | (8) |
式中:Ns为投入的限流措施的总数; us是表示决策变量是否投入的控制变量, 当us=1时表示采取了相应的限流措施, 当us=0时, 表示限流措施未投入。
限流措施的应用会引起电力系统网架结构和参数的变化, 一般会增大节点间的电气距离, 导致网架结构的松散化和系统短路容量的下降。而系统的短路容量与其稳定性成正比[21], 过度降低短路电流会影响系统的稳定性。因此, 为保证电网的稳定性, 定义表示网络紧密程度的目标函数
| $ \min {f_2} = \sum\limits_{k = 1}^N {\frac{{I_{k,1}^{\max } - {{I'}_{k,1}}}}{{{{I'}_{k,1}}}}} + \sum\limits_{k = 1}^N {\frac{{I_{k,0}^{\max } - {{I'}_{k,0}}}}{{{{I'}_{k,0}}}}} $ | (9) |
式中:N为网络中所有节点的总数; Ik, 1max和Ik, 0max分别为节点k处的三相短路电流控制上限和单相短路电流控制上限, 一般分别取为小于此处断路器遮断容量的数值; I′k, 1和I′ka, 0分别为节点k处采用限流措施后的三相短路电流和单相短路电流, 反映节点k处的短路容量。该目标函数直接反映了采取限流措施后系统短路容量的变化, 系统短路容量下降得越少, 系统稳定性才能保持得更好。
在限流优化过程中, 短路电流在控制范围内是最重要的约束条件, 也是限流优化的主要目标, 除此之外, 还需要满足一些体现系统合理运行的约束条件, 如潮流约束、支路功率约束、节点电压约束等, 具体如式(10)所示:
| $ \left\{ \begin{gathered} 没有孤立节点; \hfill \\ {P_i} = {V_i}\sum\limits_{j = 1}^{{N_b}} {{V_j}\left( {{G_{ij}}\cos {\delta _{ij}} + B\sin {\delta _{ij}}} \right),i = 1,2, \cdots {N_b};} \hfill \\ {Q_i} = {V_i}\sum\limits_{j = 1}^{{N_b}} {{V_j}\left( {{G_{ij}}\sin {\delta _{ij}} + B\cos {\delta _{ij}}} \right),i = 1,2, \cdots {N_b};} \hfill \\ {I_{k,1}} \leqslant I_{k,1}^{\max },k = 1,2 \cdots {N_b}; \hfill \\ {I_{k,0}} \leqslant I_{k,0}^{\max },k = 1,2 \cdots {N_b}; \hfill \\ {S_l} \leqslant S_l^{\max },l = 1,2 \cdots {N_l}; \hfill \\ V_k^{\min } \leqslant {V_k} \leqslant V_k^{\min },k = 1,2 \cdots {N_e}; \hfill \\ z_s^{\min } \leqslant {z_s} \leqslant z_s^{\min },s = 1,2 \cdots {N_e}; \hfill \\ \end{gathered} \right. $ | (10) |
式中:Slmax为支路l的功率控制上限, 包括支路上的有功功率和无功功率; Vkmax和Vkmin分别为节点k的电压控制上限和下限, 只考虑电压的稳态有效值; zsmax和zsmin分别为限流设备的参数变量取值的上限和下限。
3.2 求解方法交流系统综合限流优化的求解是一个非凸、非线性、离散化的复杂优化问题, 其计算模型十分复杂, 涉及的变量十分繁多, 既包含等式约束又包含不等式约束, 不便于用传统的数学优化方法进行求解。自适应混合PSO算法, 作为传统PSO算法的改进和发展, 在传统PSO算法的基础上引入了遗传的思想, 将PSO粒子的更新采用遗传算法中的交叉和变异来实现[22], 更适合限流措施优化配置这样的离散优化问题的求解。采用自适应混合PSO算法求解交流系统的综合限流优化时, 需要注意以下三个方面。
(1)粒子编码
对基于对象灵敏度排序筛选出的限流措施配置对象进行PSO粒子编码, 编码的PSO粒子的长度为N, 且N=Nb+Nl+Nt, 每个粒子分为3个子串(母线子串Nb位、线路子串Nl位和变压器子串Nt位), 如图 2所示。

|
图 2 限流措施的PSO粒子编码 Figure 2 PSO partical coding for limiting measures |
其中, 线路子串和母线子串的编码方式可参照文献[23], 而变压器子串的编码方式具体为:ti是变压器子串第i位的值, 它可以取([-timax, 2, -timin, 2], 0, [timin, 1, timax, 1])中的任意整数。若ti取[-timax, 2, -timin, 2]中的任意整数, 表示在变压器i的中性点上加装ti的电抗; 若ti取0, 表示在变压器支路i上不采用限流措施; 若ti取[timin, 1, timax, 1]中的任意整数, 表示采取了更换高阻抗变压器的操作, 在变压器支路i上增加ti的短路电压百分比增量。
(2)适应度函数
将综合限流优化的约束条件式(10)以罚值形式加入目标函数中, 构造适应值函数
| $ f = {\lambda _1}{f_1} + {\lambda _2}{f_2} + M, $ | (11) |
式中, λ1、λ2分别为两个目标函数为权重系数; M为表示约束条件满足与否的罚值, 若式(10)的所有约束条件均得到满足, 则M取为0;若式(10)中的约束条件没有全部得到满足, 则M取一充分大的正值。需要注意的是, f1的数值往往比f2大很多, 如果直接相加可能造成f2信息被湮没, 因此, 式(11)中的f1和f2均为实际目标函数的归一化计算值。
(3)方案校核
通过对综合限流优化模型进行求解, 可以得到包含多个较优限流方案的集合。集合中的各方案显然都能满足同时限制单相短路电流和三相短路电流的约束, 但在实际工程应用中, 对限流方案的选择还必须考虑系统的潮流分布均衡性、暂态稳定性和N-1供电可靠性等问题。这些问题都涉及复杂的仿真计算, 难以反映在数学优化模型中, 解决方法一般是采用专业的仿真软件对各个方案进行各方面的校核, 然后根据实际需求选择通过校核的最优方案即可。
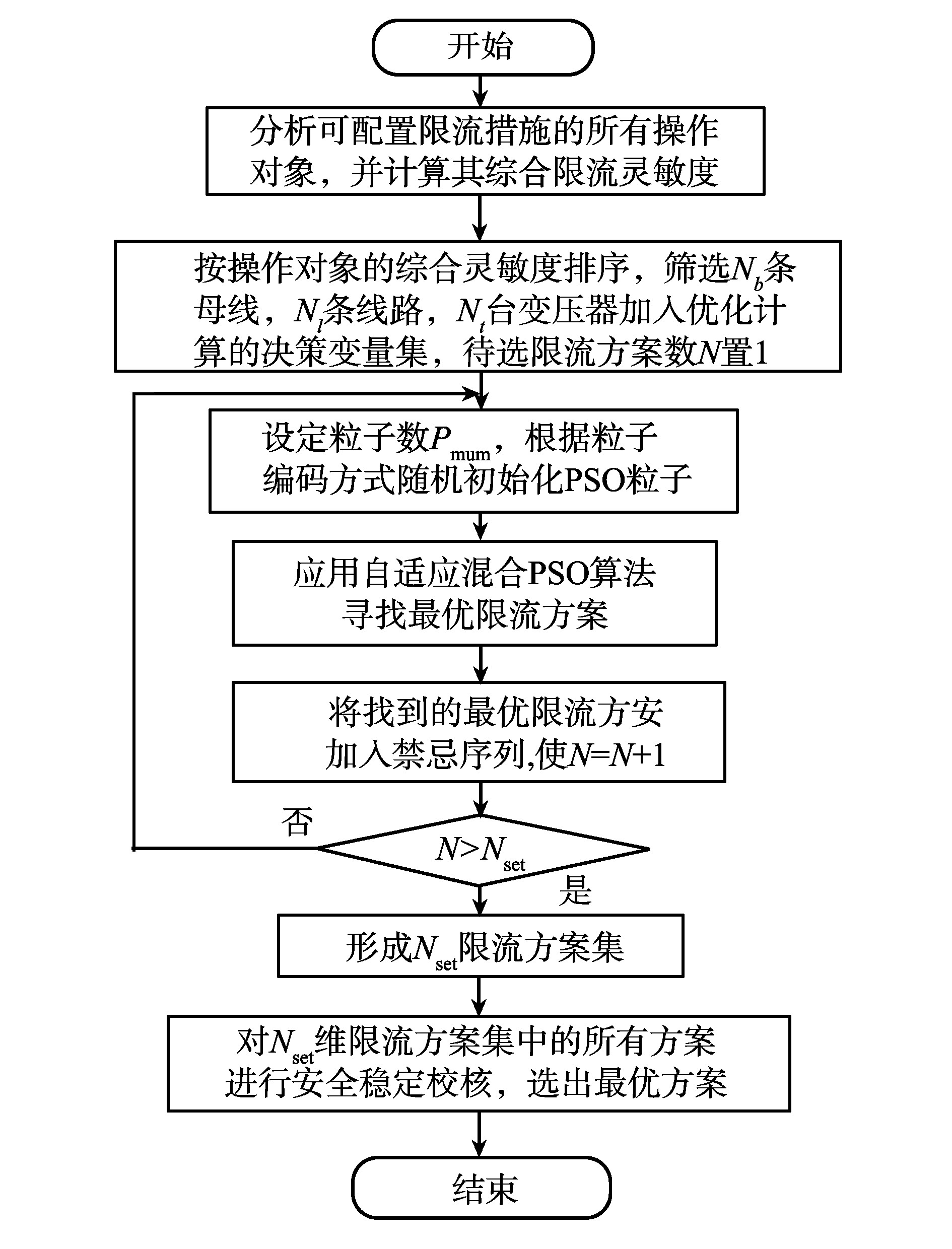
综合以上分析, 综合限流优化的方法流程如图 3所示, 图中Nset为设定的待选最优限流方案个数, 通过Nset次寻优计算后, 即可得到Nset维的待选限流方案集。
|
图 3 应用自适应混合PSO算法的综合限流优化流程 Figure 3 Comprehensive limiting optimization using self-adaptive hybrid PSO algorithm |
随着特高压输电工程的不断推进, 山东电网的特高压骨干网架逐渐形成, 原有的500 kV和220 kV网络应逐渐实现分区运行[24]。但分区运行的实现需要一定的时间, 在这期间会出现电磁环网的运行方式, 导致原有的500 kV和220 kV网络短路电流的升高。本研究以济宁地区220 kV规划电网为例验证所提综合限流优化方法的有效性, 济宁地区电网的主网架结构如图 4所示, 设定断路器最大遮断电流为50 kA, 短路电流控制上限为47.5 kA。

|
图 4 济宁地区电网结构 Figure 4 Jining regional power system structure |
限流优化前220 kV母线短路电流超标情况如表 1所示, 可见汶上站的单相短路电流以及汶上站、济宁站、济宁厂的三相短路电流都出现了超标的情况。
| 表 1 济宁地区电网220 kV母线短路电流超标情况 Table 1 220 kV buses with exceeding SCC in Jining region power system |
设定限流优化的参数为:线路串联电抗的阻抗值范围为0~10 Ω, 中性点电抗的取值范围为自耦变压器高中压短路电压百分比的1/10~1/3, 高阻抗变压器的短路电压增量范围为0~10%, 适应度函数的权重系数λ1=0.5, λ2=0.5, 各限流措施的成本系数如表 2所示[25]。
| 表 2 限流措施的成本系数 Table 2 Cost coefficients of different limiting measures |
济宁220 kV地区电网规模较大, 其中限流措施配置对象很多, 可以根据限流措施配置对象的对象灵敏度进行筛选。按照对象灵敏度降序排序, 选取本地区电网内的前50回220 kV线路, 前20条220 kV母线以及前20台变压器加入到限流优化的决策变量集合中, 因此PSO粒子的长度为90位。在采用自适应混合PSO算法进行优化计算时, 粒子群规模取为30, 收敛判据设为60次迭代计算的全局极值之差小于0.000 1。设Nset=3, 计算得到的最优限流方案集如表 3所示。
| 表 3 济宁地区电网的限流方案 Table 3 Limiting schemes of Jining region power system |
由表 3可见, 3个限流方案都能满足同时限制单相短路电流和三相短路电流的要求。采用专业软件BPA分别对3个限流方案进行潮流计算、暂态稳定计算和N-1可靠性的校核, 结果表明3个方案也都能满足安全稳定运行的要求。若按照适应值函数的大小比较, 方案1显然是最优的限流方案, 但由于实际运行条件和需求侧重的不同, 最优方案的选择也可能是不同的。
5 结语针对电网实际运行中单相短路电流超标的问题, 提出了同时限制单相和三相短路电流的综合限流优化方法。首先对单相短路电流超标的原因及其专用限流措施进行了分析, 并对通用的限流措施和单相专用限流措施的限流灵敏度和经济性进行了统一的描述。然后定义限流措施配置对象的对象灵敏度指标, 并提出了限流措施配置对象的筛选策略。以限流方案的经济性和电网结构紧密性为目标函数, 以三相短路电流和单相短路电流不超过控制上限为主要约束条件, 建立了考虑单相短路电流控制的综合限流优化模型, 并应用自适应混合PSO算法进行了求解。济宁地区规划电网的计算分析表明, 本研究所提出的综合限流优化方法能够得到同时限制单相和三相短路电流的最优限流方案。
| [1] |
刘振亚.
全球能源互联网[M]. 北京: 中国电力出版社, 2015 .
( 0) 0)
|
| [2] |
覃琴, 郭强, 周勤勇, 等. 国网"十三五"规划电网面临的安全稳定问题及对策[J].
中国电力 , 2015, 48 (1) : 25-32 QIN Qin, GUO Qiang, ZHOU Qingyong, et al. The security and stablity of power grid in 13th five-year planning and countermeasures[J]. Electric Power , 2015, 48 (1) : 25-32 (  0) 0)
|
| [3] |
NAGATA M, TANAKA K, TANIGUCHI H. FCL location selection in large scale power system[J].
IEEE Transactions on Applied Superconductivity , 2001, 11 (1) : 2489-2494 DOI:10.1109/77.920370 ( 0) 0)
|
| [4] |
SARMIENTO H G, CASTELLANOS R, PAMPIN G, et al. An example in controlling short circuit levels in a large metropolitan area[C]//Power Engineering Society General Meeting. Toronto: IEEE, 2003: 2399-2404.
( 0) 0)
|
| [5] |
HONGESOMBUT K, MITANI Y, TSUJI K. Optimal location assignment and design of superconducting fault current limiters applied to loop power systems[J].
IEEE Transactions on Applied Superconductivity , 2003, 13 (2) : 1828-1831 DOI:10.1109/TASC.2003.812901 ( 0) 0)
|
| [6] |
KIM S Y, BAE I S, KIM J O. An optimal location for superconducting fault current limiter considering distribution reliability[C]//Power and Energy Society General Meeting. Minneapolis, U S A: IEEE, 2010: 1-5.
( 0) 0)
|
| [7] |
TENG J H, LU C. Optimum fault current limiter placement with search space reduction technique[J].
Generation, Transmission & Distribution, IET , 2010, 4 (4) : 485-494 ( 0) 0)
|
| [8] |
张永康, 蔡泽祥, 李爱民, 等. 限制500 kV电网短路电流的网架调整优化算法[J].
电力系统自动化 , 2009, 33 (22) : 34-39 ZHANG Yongkang, CAI Zexiang, LI Aimin, et al. An optimization algorithm for short-circuit limitation of 500 kV power grid by adjusting power grid configuration[J]. Automation of Electric Power Systems , 2009, 33 (22) : 34-39 (  0) 0)
|
| [9] |
胡文旺, 卫志农, 孙国强, 等. 基于灵敏度法的超导故障限流器的优化配置[J].
电力系统自动化 , 2012, 36 (22) : 62-67 HU Wenwang, WEI Zhinong, SUN Guoqiang, et al. Optimal allocation of superconducting fault limiters based on sensitivity method[J]. Automation of Electric Power Systems , 2012, 36 (22) : 62-67 (  0) 0)
|
| [10] |
陈丽莉, 黄民翔, 张弘, 等. 电网限流措施的优化配置[J].
电力系统自动化 , 2009, 33 (11) : 38-42 CHEN Lili, HUANG Minxiang, ZHANG Hong, et al. An optimization strategy for limiting short circuit current[J]. Automation of Electric Power Systems , 2009, 33 (11) : 38-42 (  0) 0)
|
| [11] |
陈丽莉, 黄民翔, 许诺, 等. 考虑潮流约束的限流措施优化配置[J].
高电压技术 , 2010, 36 (6) : 1572-1576 CHEN Lili, HUANG Minxiang, XU Nuo, et al. Optimal strategy for short-circuit limiters deployment considering power flower[J]. High Voltage Engineering , 2010, 36 (6) : 1572-1576 (  0) 0)
|
| [12] |
刘树勇, 孔昭兴, 张来. 天津电网220 kV短路电流限制措施研究[J].
电力系统保护与控制 , 2009, 37 (21) : 103-107 LIU Shuyong, KONG Zhaoxing, ZHANG Lai. Application of measures of limiting 220 kV short circuit currents in Tianjin power grid[J]. Power System Protection and Control , 2009, 37 (21) : 103-107 (  0) 0)
|
| [13] |
陆国庆, 姜新宇, 江健武, 等. 110 kV及220 kV系统变压器中性点经小电抗接地方式的研究及其应用[J].
电网技术 , 2006, 30 (1) : 70-74 LU Guoqing, JIANG Xinyu, JIANG Jianwu, et al. Research on neutral grounding via small reactor for 110 kV and 220 kV power transformers and its application[J]. Power System Technology , 2006, 30 (1) : 70-74 (  0) 0)
|
| [14] |
梁纪峰, 刘文颖, 梁才, 等. 500 kV自耦变中性点串接小电抗对接地短路电流限制效果分析[J].
电力系统保护与控制 , 2011, 39 (13) : 96-99 LIANG Jifeng, LIU Wenying, LIANG Cai, et al. Analysis of limiting effect of 500 kV autotransformer neutral grounding by small reactance on ground short-circuit current[J]. Power System Protection and Control , 2011, 39 (13) : 96-99 (  0) 0)
|
| [15] |
朱天游. 三峡电站500 kV主变压器中性点接地方式优化选择[J].
电网技术 , 1997, 21 (5) : 48-51 ZHU Tianyou. Optimal selection of 500 kV main transformer neutral grounding in Three Gorges hydroelectric power station[J]. Power System Technology , 1997, 21 (5) : 48-51 (  0) 0)
|
| [16] |
朱天游. 500 kV自耦变压器中性点经小电抗接地方式在电力系统中的应用[J].
电网技术 , 1999, 23 (4) : 15-18 ZHU Tianyou. Application of autotransformer neutral grounding by small reactance in 500 kV power system[J]. Power System Technology , 1999, 23 (4) : 15-18 (  0) 0)
|
| [17] |
YANG D, ZHAO K, ZHAO Y, et al. Optimization and decision for limiting short circuit current considering sensitivity ranking[C]//2014 International Conference on Power System Technology (POWERCON). Chengdu: IEEE, 2014: 864-870.
( 0) 0)
|
| [18] |
HUANG H, XU Z, LIN X. Improving performance of multi-infeed HVDC systems using grid dynamic segmentation technique based on fault current limiters[J].
IEEE Transactions on Power Systems , 2012, 27 (3) : 1664-1672 DOI:10.1109/TPWRS.2012.2187316 ( 0) 0)
|
| [19] |
CHEN L, HUANG M, WU J, et al. An optimal strategy for short circuit current limiter deployment[C]//2010 Asia-Pacific Power and Energy Engineering Conference. Chengdu: IEEE, 2010: 1-4.
( 0) 0)
|
| [20] |
TANAKA K, TAKAHASHI K. An efficient method of modifying Z-matrix elements in short-circuit capacity calculations[J].
Electrical Engineering in Japan , 1994, 114 (2) : 48-56 DOI:10.1002/(ISSN)1520-6416 ( 0) 0)
|
| [21] |
代飞, 崔挺, 徐箭, 等. 基于综合灵敏度分析的电压校正控制[J].
电力自动化设备 , 2011, 31 (12) : 15-20 DAI Fei, CUI Ting, XU Jian, et al. Voltage correction control based on comprehensive sensitivity analysis[J]. Electric Power Automation Equipment , 2011, 31 (12) : 15-20 (  0) 0)
|
| [22] |
ZHANG W, LIU Y. Multi-objective reactive power and voltage control based on fuzzy optimization strategy and fuzzy adaptive particle swarm[J].
International Journal of Electrical Power & Energy Systems , 2008, 30 (9) : 525-532 ( 0) 0)
|
| [23] |
YANG D, ZHAO K, LIU Y. Coordinated optimization for controlling short circuit current and multi-infeed DC interaction[J].
Journal of Modern Power Systems and Clean Energy , 2014, 2 (4) : 374-384 DOI:10.1007/s40565-014-0081-z ( 0) 0)
|
| [24] |
于松青, 侯承昊, 孙英涛. 基于系统动力学的山东省电力需求预测[J].
山东大学学报(工学版) , 2015, 45 (6) : 91-98 YU Songqing, HOU Chenghao, SUN Yingtao. Power demand forecasting in Shandong province with system dynamics[J]. Journal of Shandong University (Engineering Science) , 2015, 45 (6) : 91-98 (  0) 0)
|
| [25] |
杨冬, 周勤勇, 刘玉田. 基于灵敏度分析的限流方案优化决策方法[J].
电力自动化设备 , 2015, 35 (5) : 111-118 YANG Dong, ZHOU Qinyong, LIU Yutian. Short circuit current limiting strategy optimization based on sensitivity analysis[J]. Electric Power Automation Equipment , 2015, 35 (5) : 111-118 (  0) 0)
|




