随着数字信息与互联网技术的迅速发展, 对通过互联网数字信息下载、复制、传播的安全性问题提出严重的挑战, 特别是保证图像信息安全更是未来加密算法研究的重要方向。目前, 数字图像加密算法主要分为空域和频域算法。空域算法的优点是加密后图像的大小不会发生变化, 加密过程中不会引入额外的图像畸变, 运算量较小; 频域算法一般存在数据精度的损失, 解密后引起图像失真。文献[1]采用N维仿射变换的图像加密算法; 文献[2]提出加密图像的自适应算法; 文献[3]提出基于Arnold变换图像置乱算法。文献[1-3]所提出的算法仅限于灰度图像, 加密算法比较单一, 没有综合运用扩散和置乱, 容易被攻击, 安全性较弱。文献[4]提出基于耦合二维分段混沌映射的彩色图像加密算法; 文献[5]提出基于一次时间密钥和鲁棒混沌映射的彩色图像加密; 文献[6]提出基于耦合非线性混沌映射的彩色图像加密。虽然文献[4-6]实现了彩色图像的加密, 但采用的算法中仅仅用混沌映射加密, 加密难度较低, 图像的安全性不高。因此本研究设计一种新型的彩色图像加密算法, 用复合混沌系统和仿射变换分别加密彩色图像的RGB分量, 并运用联合置乱和扩散算法加密, 增强图像的安全性、提高密钥空间和抵抗攻击的能力。
1 四进制复合混沌系统混沌系统在多媒体信息加密方面得到了较广泛的应用, 但单一混沌系统会造成混沌退化, 而且算法仅依赖于混沌系统的简单结构和密钥, 破解难度较低。本研究提出通过tent映射和改写Logistic、Cubic、Chebychev映射构造四进制复合混沌系统[7-9]。
四进制复合混沌系统构造方法:
| $ \left\{ \begin{array}{l} {\rm{Chaos}}\;{\rm{1:}}{x_{n + 1}} = \lambda - \left( {1 + \lambda } \right)\left| {{x_n}} \right|;\\ {\rm{Chaos}}\;{\rm{2:}}{x_{n + 1}} = 1 - \left( {1.5 + \lambda } \right)x_n^2;\\ {\rm{Chaos}}\;{\rm{3:}}{x_{n + 1}} = \left( {3.5 + \lambda } \right)x_n^3 - \left( {2.5 + \lambda } \right){x_n};\\ {\rm{Chaos}}\;{\rm{4:}}{x_{n + 1}} = \cos \left[{\left( {2 + 100\lambda } \right)\arccos \left( {{x_n}} \right)} \right]. \end{array} \right. $ | (1) |
| $ {Q_j} = \left\{ \begin{array}{l} 11\quad {\rm{Chaos}}{1_j} > {\rm{Chaos}}{2_j}且{\rm{Chaos}}{3_j} > {\rm{Chaos}}{4_j};\\ 10\quad {\rm{Chaos}}{1_j} > {\rm{Chaos}}{2_j}且{\rm{Chaos}}{3_j} \le {\rm{Chaos}}{4_j};\\ 01\quad {\rm{Chaos}}{1_j} \le {\rm{Chaos}}{2_j}且{\rm{Chaos}}{3_j} > {\rm{Chaos}}{4_j};\\ 00\quad {\rm{Chaos}}{1_j} \le {\rm{Chaos}}{2_j}且{\rm{Chaos}}{3_j} \le {\rm{Chaos}}{4_j}. \end{array} \right. $ | (2) |
其中:λ∈(0, 0.5), x0∈(-1, 1), j=1, 2, ,…, n, 则四进制复合混沌序列为Q{Q1, Q2, …, Qn}, 用四进制复合混沌序列实现数据加密处理, 克服加密算法被破译的可能性。
2 仿射变换仿射变换采用三维类仿射变换, 三维类仿射变换方程组的系数为实数, 构造灵活复杂使得图像信息的安全性得到提高。
定义有限整数域上的三维类仿射变换为
| $ \begin{array}{l} \quad \quad \;\left| {\begin{array}{*{20}{l}} {x'}\\ {y'}\\ {z'} \end{array}} \right| = \left| {\begin{array}{*{20}{l}} {{a_0}\quad {b_0}\quad {c_0}}\\ {{a_1}\quad {b_1}\quad {c_1}}\\ {{a_2}\quad {b_2}\quad {c_2}} \end{array}} \right|\left| {\begin{array}{*{20}{l}} x\\ y\\ z \end{array}} \right| + \left| {\begin{array}{*{20}{l}} {{d_0}}\\ {{d_1}}\\ {{d_2}} \end{array}} \right|\,\bmod \,\left| {\begin{array}{*{20}{l}} {{m_0}}\\ {{m_1}}\\ {{m_2}} \end{array}} \right| = \\ \left| {\begin{array}{*{20}{l}} {\left\lfloor {{a_0}x + {b_0}y + {c_0}z + 0.5} \right\rfloor }\\ {\left\lfloor {{a_1}x + {b_1}y + {c_1}z + 0.5} \right\rfloor }\\ {\left\lfloor {{a_2}x + {b_2}y + {c_2}z + 0.5} \right\rfloor } \end{array}} \right| + \left| {\begin{array}{*{20}{l}} {\left\lfloor {{d_0} + 0.5} \right\rfloor }\\ {\left\lfloor {{d_1} + 0.5} \right\rfloor }\\ {\left\lfloor {{d_2} + 0.5} \right\rfloor } \end{array}} \right|\,\bmod \,\left| {\begin{array}{*{20}{l}} {{m_0}}\\ {{m_1}}\\ {{m_2}} \end{array}} \right|, \end{array} $ | (3) |
其中:{a0, b0, c0, d0, a1, b1, c1, d1, a2, b2, c2, d2}为实数, {m0, m1, m2}为正整数, {x′, y′, z′, x, y, z}为非负整数且{x′, x}∈[0, m0-1], {y′, y}∈[0, m1-1], {z′, z}∈[0, m2-1],
对式(3)参数进行适当设置, 可以得到式(4)或式(5):
| $ \left| \begin{array}{l} {x'}\\ {y'}\\ {z'} \end{array} \right| = \left| {\begin{array}{*{20}{c}} {1 + {a_1}n{q_1}}&{n{q_1}}&0\\ {{a_1}}&1&0\\ {{a_2}}&{{b_2}}&{{c_2}} \end{array}} \right|\left| \begin{array}{l} x\\ y\\ z \end{array} \right| + \left| \begin{array}{l} {d_0}\\ {d_1}\\ {d_2} \end{array} \right|\bmod \left| \begin{array}{l} {m_0}\\ {m_1}\\ {m_2} \end{array} \right|, $ | (4) |
| $ \left| \begin{array}{l} {x'}\\ {y'}\\ {z'} \end{array} \right| = \left| {\begin{array}{*{20}{c}} 1&{{b_0}}&0\\ {n{q_2}}&{1 + {b_0}n{q_2}}&0\\ {{a_2}}&{{b_2}}&{{c_2}} \end{array}} \right|\left| \begin{array}{l} x\\ y\\ z \end{array} \right| + \left| \begin{array}{l} {d_0}\\ {d_1}\\ {d_2} \end{array} \right|\bmod \left| \begin{array}{l} {m_0}\\ {m_1}\\ {m_2} \end{array} \right|, $ | (5) |
其中: q1=m0/gcd(m0, m1), q2=m1/gcd(m0, m1), a1∈Z1, b0∈Z0, nq1∈Z0, nq2∈Z1, 1+a1nq1∈Z0, 1+b0nq2∈Z1, gcd(c2, m2)=1, 为简化计算{a2, b2, c2, d0, d1, d2}取为整数, Z0为模m0的剩余类, Z1为模m1的剩余类。用式(3)~式(5)不仅实现了像素位置置乱, 而且实现了像素值的置换[9]。
3 加密算法设计(1)根据式(1)确定4个混沌序列的初始参数x0和λ, 初始值共8个参数, 由式(2)生成复合混沌序列Q。设置24个参数分别产生加密RGB分量的复合混沌序列Qr0(红色)、Qg0(绿色)和Qb0(蓝色), 随机取3个整数kr0、kg0和kb0作为序列的截取点。
(2)将原始彩色图像i0读到M×N×3三维矩阵P0中, P0=[R0, G0, B0], 其中: R0、G0、B0分别表示二维红、绿、蓝矩阵, 像素的值为0到255。
(3)将P0置换成P1, 即由P0和对应的复合混沌序列异或生成加密图像。在生成复合混沌序列的过程中根据每一行像素值对x0和λ进行扰动, 第一行扰动第二行, 逐行扰动, 最后一行扰动第一行, 以实现像素值的扩散, 其扰动公式为:x01=[x0+(k0+1)/255]/2, λ1=[λ+(k0+1)/510]/2, 其中:k0是一行像素的平均值。
| $ \begin{array}{l} {R_1} = {R_0} \oplus {Q_{{\rm{r}}0}};\\ {G_1} = {G_0} \oplus {Q_{{\rm{g}}0}};\\ {B_1} = {B_0} \oplus {Q_{{\rm{b}}0}};\\ {P_1} = \left[{{R_1},{G_1},{B_1}} \right]. \end{array} $ |
其中:R1、G1、B1分别为R0、G0、B0经复合混沌加密后的图像; P1是由R1、G1、B1构成的复合混沌加密图像。
(4)根据式(3)~(5)将置换图像P1置换成P2, 分别设计仿射变换的初始参数生成RGB仿射变换方程组Ar1、Ag1和Ab1, 并对RGB分量进行不同的变换次数。
R2=R1三维类仿射变换Ar1, 变换次数Nr1;
G2=G1三维类仿射变换Ag1, 变换次数Ng1;
B2=B1三维类仿射变换Ab1, 变换次数Nb1;
P2=[R2、G2、B2]。
其中: P2是由R2、G2、B2构成的仿射变换加密图像。
(5)对P2进行联合置换生成Pu1, 设置24个参数分别产生加密RGB分量的复合混沌序列Qr1(红色)、Qg1(绿色)和Qb1(蓝色), 随机取3个整数kr1、kg1和kb1作为序列的截取点。P2数组和对应的扰动复合混合混沌序列异或加密处理。
将R2分解成R2=[Rleft、Rcentrer、Rright]三部分, 其中: Rleft、Rcentrer、Rright为R2矩阵的左边、中间和右边的三分之一;
将G2分解成G2=[Gleft、Gcentrer、Gright]三部分, 其中: Gleft、Gcentrer、Gright为G2矩阵的左边、中间和右边的三分之一;
将B2分解成B2=[Bleft、Bcentrer、Bright]三部分, 其中: Bleft、Bcentrer、Bright为B2矩阵的左边、中间和右边的三分之一。
Ru0=[Rleft、Gcenter、Bright];
Gu0=[Gleft、Bcenter、Rright];
Bu0=[Bleft、Rcenter、Gright]。
Ru1=Ru0⊕Qr1;
Gu1=Gu0⊕Qg1;
Bu1=Bu0⊕Qb1;
Pu1=[Ru1, Gu1, Bu1]。
其中: Ru1、Gu1、Bu1是由Ru0、Gu0、Bu0复合混沌加密后的图像; Pu1是由Ru1、Gu1、Bu1构成的复合混沌加密图像。
(6)对Pu1进行联合置乱生成加密彩色图像Pu2, 分别对Ru1, Gu1, Bu1矩阵进行Ar2、Ag2、Ab2仿射变换, Ar2、Ag2、Ab2是分别设计仿射变换的初始参数生成RGB仿射变换方程组。
Ru2=Ru1仿射变换Ar2, 变换次数Nr2;
Gu2=Gu1仿射变换Ag2, 变换次数Ng2;
Bu2=Bu1仿射变换Ab2, 变换次数Nb2;
Pu2=[Ru2、Gu2、Bu2]。
其中: Pu2是由Ru2、Gu2、Bu2构成的仿射变换加密图像。
经过以上步骤, 完成了一次加密过程, 根据图像安全等级, 可以增加加密的次数, 最终得到加密图像i1[10]。解密过程是加密过程的逆过程, 其彩色图像的加密过程如图 1。
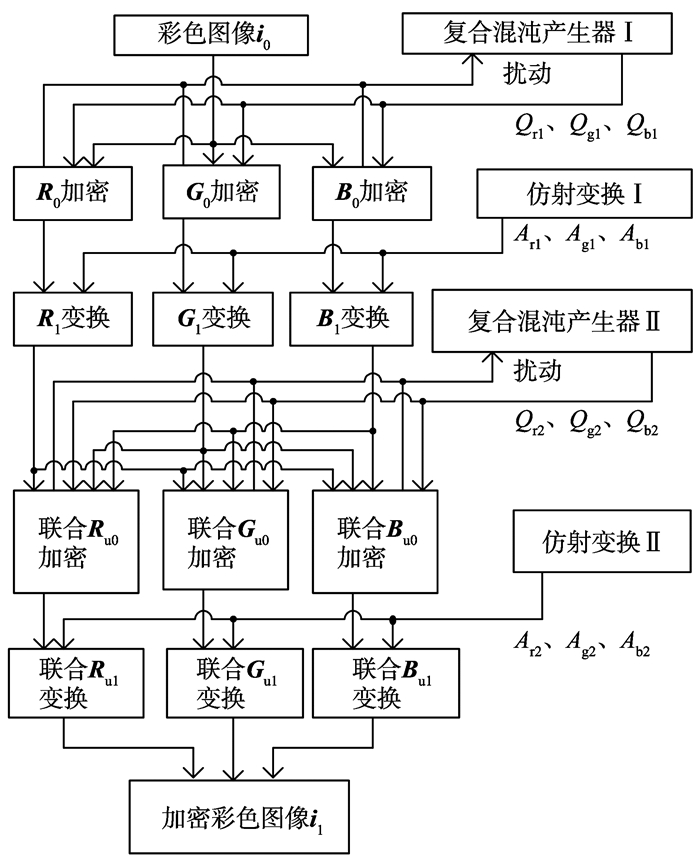
|
图 1 彩色图像加密过程 Figure 1 Color image encryption process |
应用MATLAB7.0平台实现了本研究提出的加密算法, 彩色图像为512×512的bmp文件, 分别选择水印(baboon)、风景(花草和青山)和人物(男女卡通)图像为例进行加密处理, 其加密一次的结果如图 2, 通过视觉分析图 2很难辩别出加密前的图像。

|
图 2 彩色图像及RGB分量加密结果 Figure 2 Color images and the RGB components encryption results |
加密算法中密钥参数包括Chaos1到Chaos4复合混沌公式共8个实数, 实数取10位有效数字, 截取复合混沌序列有效起始位为3位整数, 两次复合混沌置换, 则RGB分量中一个分量的复合混沌密钥空间为103×2×1010×8×2=10166; 三维类仿射变换的初始参数为:q1(或q2), a1(或b0), n由m0、m1、m2和对应剩余类决定, 这些参数构成的密钥空间省略, 图像仿射变换初始变换次数为3位整数, a2, b2, c2, d0, d1, d2设为2位整数, 考虑两次仿射变换密钥空间, 则RGB分量中一个分量的仿射变换的密钥空间为103×2×102×6×2=1030。因此一次加密过程的密钥空间是10166×1030=10196>2498, 用穷举攻击来解密图像是相当困难。如果要提高图像的安全等级, 可以通过多次加密实现。本研究密钥空间与其他文献加密空间比较如表 1所示, 分析表 1可知本研究加密算法具有较大的密钥空间。
| 表 1 本研究与其他文献密钥空间比较 Table 1 Key space of this research compared with other literature |
加密前后图像的直方图如图 3, 通过分析图 3看出加密前RGB分量直方图分布是有规律的, 加密后RGB分量直方图分布规律非常均匀, 无法辨认加密前的分布规律, 因此可有效地抵抗统计分析的攻击。
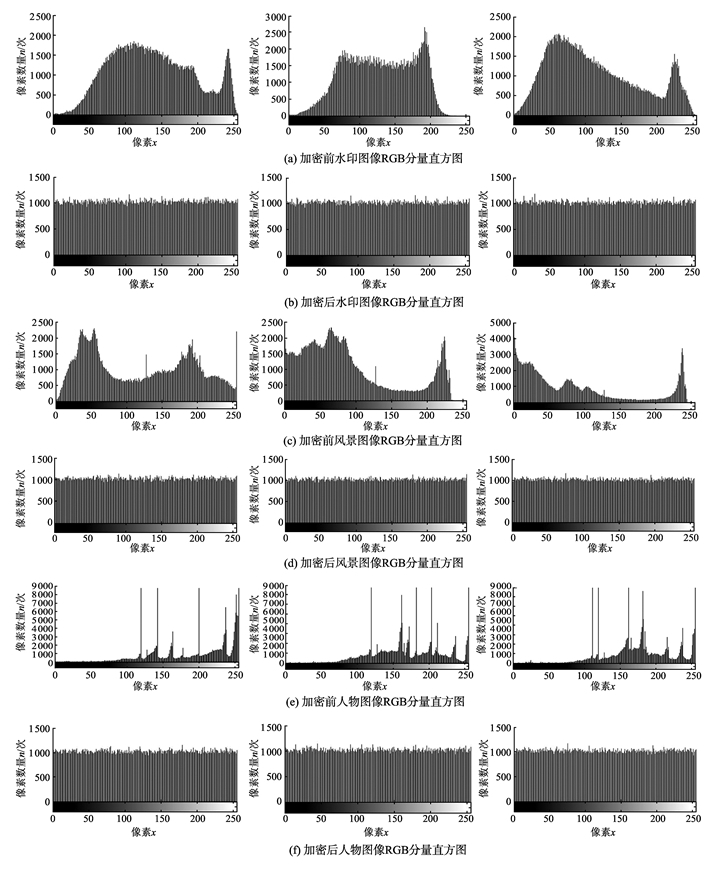
|
图 3 彩色图像RGB分量直方图 Figure 3 RGB components histogram of color image |
加密效果可以用相邻像素的相关性来进行评价, 相关性越小加密效果越好, 其离散化计算相关系数的公式为:
| $ \left\{ \begin{array}{l} r\left( {x,y} \right) = \frac{{\left| {{\mathop{\rm cov}} \left( {x,y} \right)} \right|}}{{\sqrt {D\left( x \right)} \sqrt {D\left( y \right)} }},\\ {\mathop{\rm cov}} \left( {x,y} \right) = \frac{1}{N}\sum\limits_{i = 1}^N {\left( {{x_i} - E\left( x \right)\left( {{y_i} - E\left( y \right)} \right),} \right.} \\ E\left( x \right) = \frac{1}{N}\sum\limits_{i = 1}^N {{x_i}} ,\\ D\left( x \right) = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{x_i} - E\left( x \right)} \right)}^2}} . \end{array} \right. $ | (6) |
式中:x、y表示相邻两个像素的值。本研究计算了水印、风景和人物彩色图像加密前后RGB分量平均水平、垂直和对角相关性, 并与其它文献进行了比较, 表明本研究算法加密相关性均有明显的提高, 计算结果如表 2。
| 表 2 本研究与其他文献图像的相关性 Table 2 Image correlation of this research and other literature |
通过密钥参数的微小变化来对加密图像进行解密, 测试算法的密钥敏感性。图 4是Chaos1到chaos4的λ、x0参数分别改变1×10-15对baboon加密彩色图像的解密结果, 解密得到的图像无法视别出原始图像, 证明算法具有较强的密钥敏感性。

|
图 4 密钥敏感性分析 Figure 4 Sensitivity analysis of key |
通过计算像素改变率Rnpc和平均变化强度Iuac来评价密文敏感性。设原始图像i0的加密图像为i1, i0的某个像素的值加1或减1再进行加密处理得到加密图像i2, 根据i1和i2计算Rnpc和Iuac来分析密文敏感性。其Rnpc和Iuac的计算公式为:
| $ \left\{ \begin{array}{l} {R_{{\rm{npc}}}} = {\left( {MN} \right)^{ - 1}}\left( {\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^M {q\left( {i,j} \right)} } } \right) \times 100\% ,\\ {I_{{\rm{uac}}}} = {\left( {255 \times MN} \right)^{ - 1}} \times \\ \quad \quad \left( {\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {\left| {{i_1}\left( {i,j} \right) - {i_2}\left( {i,j} \right)} \right|} } } \right) \times 100\% . \end{array} \right. $ | (7) |
当i1(x, y, z)=i2(x, y, z)时, 则q(i, j)=0, 否则q(i, j)=1。根据上式分别计算了水印、风景和人物图像RGB分量的Rnpc和Iuac, 见表 3。Rnpc的平均值>99%, Iuac的平均值>37%, 证明本研究算法具有抵抗差分攻击的能力。
| 表 3 密文敏感性计算结果 Table 3 Cipher sensitivity of computed results |
信息熵可以用来度量图像中像素值的分布情况, 像素值分布越均匀信息熵越大, 反之信息熵越小, 信息熵的最大值为8。其信息熵的计算公式为:
| $ H\left( m \right) = \sum\limits_{i = 0}^{255} {p\left( {{m_i}} \right) \times 1{\rm{b}}\left( {1/p\left( {{m_i}} \right)} \right)} , $ | (8) |
其中: p(mi)为出现mi的概率, mi某点像素的值。根据上式分别计算了水印、风景和人物彩色图像RGB分量的平均信息熵如表 4所示, 计算结果表明加密后像素值分布均匀, 算法具有较强的抵抗统计攻击的能力。
| 表 4 本研究与其它文献图像信息熵比较 Table 4 Image information entropy of this research compared with other literature |
通过峰值信噪比来衡量加密后对原始图像的掩盖程度, 峰值信噪比的计算公式为:
| $ \left\{ \begin{array}{l} {\rm{PSNR = 101}}{{\rm{g}}^{\left( {{{255}^2}/{\rm{MSE}}} \right)}},\\ {\rm{MSE = }}{\left( {MN} \right)^{ - 1}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {{{\left( {{i_0}\left( {i,j} \right) - {i_1}\left( {i,j} \right)} \right)}^2}} } \end{array} \right. $ | (9) |
其中:i0表示原始图像, i1表示加密后的图像, 根据上式分别计算水印、风景和人物图像RGB分量的平均峰值信噪比为8.808 2、7.280 4和7.281 5 dB, 当峰值信噪比小于20 dB时加密图像就完全无法辨认, 所以本研究提出的加密算法对原始图像具有较好的掩盖性。
4.9 相似度计算原始图像与加密图像相似度越小, 可辨认性越低, 保密性越强。相似度的计算公式为:
| $ \begin{array}{l} {\rm{XSD = 1}} - \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {\left( {{i_1}\left( {i,j} \right) - {i_0}{{\left( {i,j} \right)}^2}/} \right.} } \\ \quad \quad \quad \;\,\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {\left. {{i_0}{{\left( {i,j} \right)}^2}} \right)} } , \end{array} $ | (10) |
其中:i0表示原始图像, i1表示加密后的图像, 当i0和i1相同时, XSD等于1。根据式(10)分别计算水印、风景和人物图像RGB分量的平均相似度为0.543 8、0.058 1和0.685 2, 计算结果表明相似度较小, 明密图像差异显著, 隐藏性较强。文献[9]计算的相似度小于0.646, 本研究算法人物图像比文献[9]略高0.039 2。
5 结论根据本研究提出的算法利用matlab7.0平台分别对lena、baboon、peppers彩色图像、internet上下载的风景、人物和植物等50多幅彩色图像进行了加密仿真试验, 其直方图、相邻像素相关性、密文敏感性、信息熵、峰值信噪比和相似度的计算结果表明加密图像后密钥空间大, 无法辨认加密前的分布规律, 相似度和相关性小, 具有抵抗差分和统计分析的攻击的能力。算法加密安全性高, 速度快, 在军事和电子商务领域具有较高的应用价值。
本研究的创新点:(1)提出了四进制复合混沌序列生成模型, 提高了加密算法被破译的难度。(2)设计了三维仿射变换的数学模型, 实现了像素位置置乱和像素值的置换。(3)设计了彩色图像RGB分量的单独、联合置乱和扩散加密方案, 提高了算法抵抗攻击的能力。
| [1] |
WANG F C, BAI S, ZHU G B, et al. An image encryption algorithn based on N-dimension affine transformation[C]// Processdings of the 8th IEEE/ACIS Int conf on Computer and Information Science. Piscataway, NJ(America): IEEE, 2009: 579-585.
( 0) 0)
|
| [2] |
CHEN G, ZHAO X Y, LI J L. A seft-adaptive algorithm on image encryption[J].
Journal of Software , 2005, 16 (11) : 1975-1982 DOI:10.1360/jos161975 ( 0) 0)
|
| [3] |
SHANG Z W, REN H E, ZHANG J. A block lacation scramling algorithm of digital image based on arnold transformatiom[C]// Processdings of the 9thInt Conf for Young Computer Scientists. Piscataway, NJ(America): IEEE, 2008: 2942-2947.
( 0) 0)
|
| [4] |
SEYEDZADEH S M, MIRZAKUCHAKI S. A fast color image encryption algorithm based on coupled two dimensional piecewise chaotic map[J].
Signal Processing , 2012, 92 (5) : 1202-1215 DOI:10.1016/j.sigpro.2011.11.004 ( 0) 0)
|
| [5] |
LIU H J, WANG X Y. Color image encryption based on one time keys and robust chaotic maps[J].
Computers and Mathematics with Applications , 2010, 59 (10) : 3320-3327 DOI:10.1016/j.camwa.2010.03.017 ( 0) 0)
|
| [6] |
SAHAR M, AMIR M E. Color image encryption based on coupled nonlinear chaotic map[J].
Chaos, Solitons & Fractals , 2009, 42 (3) : 1745-1754 ( 0) 0)
|
| [7] |
黄晓生, 顾景文. 基于复合混沌序列与小波变换的图像加密算法[J].
计算机工程 , 2007, 33 (7) : 128-129 HUANG Xiaosheng, GU Jingwen. Image encryption algorithm based on compound chaotic sequence and wavelet transform[J]. Computer Engineering , 2007, 33 (7) : 128-129 (  0) 0)
|
| [8] |
曹建秋, 肖华荣, 蓝章礼. 基于变参混沌系统的图像双重置换加密[J].
计算机工程与应用 , 2011, 47 (32) : 101-104 CAO Jianqiu, XIAO Huarong, LAN Zhangli. Image dual scrambling encryption algorithm based on chaotic system with variable parameter[J]. Computer Engineering and Application , 2011, 47 (32) : 101-104 (  0) 0)
|
| [9] |
文昌辞, 王沁, 刘向宏, 等. 基于仿射和复合混沌的图像加密新算法[J].
计算机研究与发展 , 2013, 50 (2) : 319-324 WEN Changci, WANG Qin, LIU Xianghong, et al. An encryption algorithm for image based on affine and composed chaos[J]. Journal of Computer Research and Development , 2013, 50 (2) : 319-324 (  0) 0)
|
| [10] |
谢涛, 何兴. 一种新的基于混沌的彩色图像加密方案[J].
计算机应用研究 , 2013, 30 (1) : 318-320 XIE Tao, HE Xing. New color image encryption scheme baesed on chaos[J]. Application Research of Computers , 2013, 30 (1) : 318-320 (  0) 0)
|
| [11] |
陈帅, 钟先信, 石军锋, 等. 基于离散数字混沌序列的图像加密算法[J].
电子与信息学报 , 2007, 29 (4) : 898-900 CHEN Shuai, ZHONG Xianxin, SHI Junfeng, et al. Image encrytion through discrete digital chaotic sequence[J]. Journal of Electronics & Information Technology , 2007, 29 (4) : 898-900 (  0) 0)
|
| [12] |
彭飞, 丘水生, 龙敏. 外部密钥控制系统参数的图像加密算法[J].
华南理工大学学报(自然科学版) , 2005, 33 (7) : 20-23 PENG Fei, QIU Shuisheng, LONG Min. An image encryption algorithm with parameters controlled by external keys[J]. Journal of South China University of Technology(Science and Technology) , 2005, 33 (7) : 20-23 (  0) 0)
|
| [13] |
CHEN D M. A feasible chaotic encryption scheme for image[C]//Processdings of Int Workshop on Chaos-Fractals and Applications.Piscataway, NJ(America): IEEE, 2009: 172-176.
( 0) 0)
|
| [14] |
袁野, 李敬医, 陈炬桦. 基于二维X型可逆细胞自动机的加密算法[J].
计算机应用 , 2014, 34 (12) : 3466-3469 YUAN Ye, LI Jingyi, CHEN Juhua. Encryption algorthm based on 2D X-type reversible cellular automata[J]. Journal of Computer Applications , 2014, 34 (12) : 3466-3469 (  0) 0)
|
| [15] |
WANG X, LUAN D. A image encryption algorithm using chaos and reversible cellular aotomato[J].
Communications in Nonliner Science and Numerical Simulation , 2013, 18 (11) : 3075-3085 DOI:10.1016/j.cnsns.2013.04.008 ( 0) 0)
|
| [16] |
PATIDAR V, PAREEK N K, PUROHIT G, et al. Modified substitution-diffusion image cipher using chaotic standard and logistic maps[J].
Communications in Nonliner Science and Numerical Simulation , 2010, 15 (10) : 2755-2765 DOI:10.1016/j.cnsns.2009.11.010 ( 0) 0)
|
| [17] |
邹玮刚, 陈沛云, 黄江燕. 基于三维亚仿射变换的数字图像置乱技术[J].
计算机应用 , 2012, 32 (9) : 2595-2598, 2602 ZOU Weigang, CHEN Peiyun, HUANG Jiangyan. Digital image scrambling technology based on three dimensional sub-affine transformation[J]. Journal of Computer Applications , 2012, 32 (9) : 2595-2598, 2602 (  0) 0)
|
| [18] |
杨璐, 邵利平, 郭毅, 等. 基于迷宫置换和Logistic混沌映射的图像加密算法[J].
计算机应用 , 2014, 34 (7) : 1902-1908 YANG Lu, SHAO Liping, GUO Yi, et al. Image encryption algorithm based on maze permutation and logistic chaotic map[J]. Journal of Computer Applications , 2014, 34 (7) : 1902-1908 (  0) 0)
|



